课外补习对初中生学业成绩的影响效应——基于PSM-DID方法的估计

管 振

一、引言

课外补习是指为提高学生学业成绩而进行的、正规学校外的补充性教育活动(Bray and Kwok, 2003)。早在20世纪60年代，课外补习在亚、非、拉国家已普遍存在(Baker et al., 2001)。中国因社会发展转型，课外补习市场崛起较晚(李佳丽，2018)。20世纪80年代后期，一些城市家庭父母请老师或大学生到家中为孩子辅导，成为中国现代课外补习的起源。一直到现在，这种补习形式仍然存在，但已经被更广泛的小组和大班制的校外培训所淹没(陈全功，2012)。近些年来，我国出台一系列政策鼓励减轻中小学生的校外学习负担，但课外补习率仍保持在较高水平(张冰和程天君，2019)。2012年全国有约24.6%的义务教育在校生参加了课外补习(薛海平，2015)，2017年的补习率更是超过30%(魏易和薛海平，2021)。

课外补习不仅是家庭教育竞争的重要一环，也是教育机会不均等的重要体现，受到政府和学界的广泛关注(Dang and Rogers, 2008)。学界对课外补习的研究主要集中在两个方面，分别是参与课外补习的影响因素和其对学业成绩的影响。对于前者，大多数研究发现，家庭经济水平越优、父母的教育程度越高，子女参与课外补习的概率越大(Stevenson and Baker, 1992; 洪岩璧和赵延东, 2014; 薛海平和赵阳, 2020)。因此，课外补习也被认为具有社会阶层复制的作用(薛海平和李静，2016)。根据学业成绩较优和较劣的学生有更大概率参与课外补习，可以将课外补习分为培优型和补差型(Baker et al., 2001)。研究发现，因为儒家社会，如韩国、日本和中国等对等级考试更加重视，以培优型为主(Entrich, 2014; Kim et al., 2010)。而欧美国家，如美国、英国、以色列等的补习活动多是依靠公共财政，对学习成绩不佳或贫困的学生提供支持，以补差型为主(Baker et al., 2001)。

诸多学者研究了语文、数学和英语补习对相应学科成绩的影响，还未形成统一的结论。有的学者研究发现各学科补习都有效(薛海平，2016)。与此相反，有的学者研究发现各学科补习都无效(孙伦轩和唐晶晶，2019)。也有学者研究发现部分学科补习有效，部分无效，如李波(2018)发现尽管数学和英语补习有效，但是语文补习无效；胡咏梅等(2021) 发现语文和英语补习有效，但是数学补习无效。除了不同个人特征和家庭背景等学生的补习效应存在异质性之外，没有形成统一结论的主要原因是，有些研究中存在内生性问题(胡咏梅等，2015)。

学界常常采用普通最小二乘(OLS)、倾向得分匹配(PSM)、两阶段最小二乘(2SLS)、双重差分(DID)和倾向得分匹配-双重差分(PSM -DID)等方法研究课外补习对学业成绩的影响(李波和黄斌，2020)。OLS和PSM方法的基本思想相同：依据选取的变量平衡补习和未补习学生间的异质性差异，从而得出在其他可观测特征相同的情况下，课外补习对学业成绩的影响。然而，其估计的有效性易受到遗漏变量，特别是学生的个人能力和初始成绩的影响。如果学业成绩优异的学生更倾向于参与课外补习，遗漏初始成绩变量可能会高估补习效应；反之，低估补习效应。尽管部分学者在模型中加入了初始成绩变量变量，但是学生的个人能力仍然无法控制(薛海平等，2014；李佳丽和胡咏梅，2017)。

为了克服遗漏变量问题，有些学者采用2SLS方法进行估计。其基本思想是：依据与核心解释变量(课外补习)相关，而与随机误差项不相关的外生变量，进行局部随机分组，进而得出课外补习对学业成绩的因果影响。常见的工具变量有公立学校收取的辅导费、家离补习班的距离、班级内学生的补习比例等(Dang, 2007; Zhang, 2013; Suryadarma et al.,2006; 杨莉，2020)。在相关性和外生性条件满足的情况下，2SLS方法能够估计出课外补习的局部处理效应。然而，工具变量的外生性常常难以满足；而且由于其估计的是局部处理效应，外部有效性也常常受到质疑。

近年来，有些学者尝试采用DID方法估计课外补习对学业成绩的影响。其基本思想是：如果补习的学生未补习，他(她)的成绩将和未补习的学生有着相同的变化(平行趋势假设)，则补习学生成绩的变化减去未补习学生成绩的变化，即为补习效应。为了使平行趋势假设得以满足，Heckman et al.(1997)提出使用PSM-DID方法进行估计。PSM-DID方法的基本思想是：首先，使用PSM方法估计进行样本筛选，以此平衡补习和未补习学生间的可观测特征差异；然后，利用筛选后的样本再进行DID估计。部分学者使用此方法考察了课外补习对学业成绩的影响，但是还存在一些不足；其中最主要是未将基期样本限定在未参与补习的学生当中，导致估计的结果为两期补习效应的差异(孙伦轩和唐晶晶，2019；庞晓鹏等，2017)。

鉴于目前在补习效应的研究中还未形成一致的结论，而且方法应用上还存在一些不足，本文使用中国教育追踪调查(CEPS)基线和追访数据，采用PSM-DID方法估计语文、数学和英语补习对相应学业成绩的影响；并考察其在不同学生群体间的异质性。本研究的理论意义在于：完善了PSM-DID方法在补习效应研究中的应用，进一步深化对补习效应的认识。现实意义在于：研究结论既有助于学生和家长合理分配课外学习时间；也有助于政府更有效地配置教育资源，促进教育公平和健康发展。

本文接下来的安排如下，第二部分介绍模型设定、数据来源和处理结果；第三部分报告课外补习的影响因素以及补习效应的估计结果；第四部分进一步分析补习效应的异质性以及放弃课外补习对学业成绩的影响；第五部分总结研究结论，并提出相应的政策建议。

二、模型与数据

(一)补习效应的识别

本文使用七年级和八年级学生样本，估计七、八年级间的语文、数学和英语补习对各学科成绩的影响。因为各学科补习效应的识别策略相同，下面将做一般化的讨论。

DID方法识别补习效应的思路如图1所示。首先，由于估计七、八年级间的补习效应，我们考虑学生处于七、八年级两个时点的学业成绩。其次，将样本限定在七年级前未参与补习的学生中，以使初始样本全部是未受处理的学生。再次，根据有部分学生在七、八年级间参与补习(treat=1)，有部分未参与(treat=0)，把学生分成两类。基于以上设定，在七、八年级间补习的学生的成绩变化为C0F0。因为即使未参与补习，学生的成绩在此期间也可能会发生变化(假设为E0F0)，所以补习效应为：C0E0=C0F0-E0F0。但是，E0F0无法观测。为此，用七、八年级间未补习学生的成绩变化(即D0G0)代替E0F0作为反事实。这就要求满足：B0D0∥A0E0以及D0G0=E0F0(即平行趋势假设)。

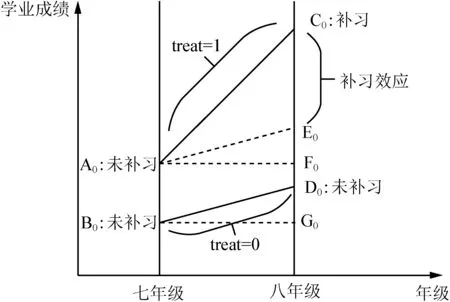
图1 DID方法对补习效应的识别

为了使平行趋势假设得以满足，使用七年级的学生样本进行PSM估计，来筛选出其他特征相似的补习和未补习的学生；然后再进行DID估计。若平行趋势假设得以满足，C0E0=C0F0-E0F0=C0F0-D0G0就反映出七、八年级间的课外补习对学业成绩的因果影响。以上即为PSM-DID估计补习效应的基本思路。

(二)模型设定

1. DID模型

根据DID方法对补习效应识别的思路，本文采用以下模型估计语文、数学和英语补习对相应学科成绩的影响：

scoreijt=α0j+α1jtreatij+α2jafterijt+α3j(treatij*afterijt)
+Xijtα4j+μijt

(1)

其中，下标j分别表示语文、数学或英语学科。t=0和t=1分别表示学生处于七、八年级。在进行j学科的估计中，仅仅使用了七年级前未参加过j学科补习的样本。当学生i在七、八年级间参加学科j的课外补习时，treatij=1；反之，treatij=0。t=0和t=1分别对应于afterijt=0和afterijt=1。scoreijt表示学生相应的考试成绩。Xijt表示模型中的控制变量集，包含学生的个人特征(性别、年龄、独生子女和城乡身份)、家庭背景(父母教育水平、家庭经济水平)、学校情况(公立学校、学校质量)、学生的寄宿状况和区县固定效应等。μijt表示对学生成绩有影响的随机扰动项。

模型(1)与图1的内容一一对应。treat=0，after=0意味着七、八年级间未补习的学生在七年级的状态，与图1中的B0点相对应；此时，score1=r；其中，r=α0j+Xijtα4j+μijt。(1)为了表达简洁，在此处的讨论中省略了部分下标；下同。同理，treat=0，after=1与图1中的D0点相对应；此时，score2=α2+r。treat=1，after=0，与图1中的A0点相对应；此时，score3=α1+r。treat=1，after=1，与图1中的C0点相对；此时，score4=α1+α2+α3+r。各状态学生对应的学业成绩如表1所示。

表1 DID模型中各状态学生的学业成绩

C0F0反映了C0与A0的成绩差，即：

C0F0=score4-score3=(α1+α2+α3+r)-(α1+r)=α2+α3

D0G0反映了D0与B0的成绩差，即：

D0G0=score2-score1=(α2+r)-r=α2

根据前文分析，补习效应C0E0为：

C0E0=C0F0-D0G0=(α2+α3)-α2=α3

即模型(1)中交互项的系数估计值反映了各学科补习对学业成绩的影响。

2. PSM-DID模型

补习效应的正确识别，依赖于平行趋势假设得以满足。为此，首先使用七年级的横截面数据进行PSM估计来筛选样本，以平衡补习和未补习学生间的特征差异；然后再利用模型(1)进行DID估计。PSM估计的基本模型为：

(2)

其中，下标t=0，意味着仅包含七年级的样本。跟前文一样，在进行j学科的估计中，仅仅使用了七年级前未参加过j学科补习的样本。其他变量的定义与模型(1)相同。此外，为了平衡七、八年级间补习和未补习学生的初始成绩差异，在模型中也加入了学生七年级的成绩scoreij0。εij0为随机误差项。

通过估计模型(2)，可以得出所有样本的倾向得分值。然后依据不同的匹配策略(如k近邻匹配、半径匹配、核匹配、马氏匹配等)进行样本筛选后，再采用模型(1)进行DID估计。即为本文所采用的PSM-DID估计模型。此外，模型(2)也被用于分析学生参与语文、数学和英语补习的影响因素。

(三)数据来源、处理与描述性统计

1. 数据来源

本文使用的数据来源于中国教育追踪调查(CEPS)的2013-2014学年基线和2014-2015学年追访数据。该数据是由中国人民大学中国调查与数据中心设计与实施的、具有全国代表性的大型追踪调查项目。其从全国随机抽取了28个县级单位(县、区、市)作为调查点，总共调查了112所学校、438个班级。在基线调查中，在七年级总共调查了10279名学生；一年后，成功追访9449名，追访率为91.9%。我们把基线调查中七年级的学生样本和一年后的追访样本(学生升为八年级)进行匹配与合并，即为本文使用的全部样本来源。

2. 数据处理

根据模型设定，选择的变量包括学生的基本信息、家庭背景、学校情况、语文、数学及英语的补习状况和考试成绩等。各变量的定义如表2所示。需要说明的是，在七年级和八年级分别询问了学生“参加了哪些兴趣班或课外辅导班”和“最近一年来，参加了哪些兴趣班或课外辅导班”，答题选项包含“没参加、数学、语文、英语及其他与课业无关的兴趣培训等”。本文据此识别出学生在七年级前和以及七、八年级间是否参加过某学科的课外补习。在各学科考试成绩的处理上，参考孙伦轩和唐晶晶(2019)的研究，标准成绩按照学校进行标准化为： (学生成绩-最低分)/(最高分-最低分)。此外，父母教育水平由问卷调查的父母最高教育程度转化而来，各阶段教育年限分别为：小学6年，初高中各3年，大专3年，本科4年，研究生3年，博士4年。

此外，为了消除特差生和特优生的影响，仅保留了在七年级语文、数学和英语成绩为1%分位到 99%分位之间的学生。

3. 描述性统计

在删除了各变量的缺失值和异常值后，共得到12474个样本。其中，七年级前未参与语文补习的样本最多，约10960个；而未参与数学和英语补习的人数相当，分别为9584和9286个。各变量描述性统计结果如表2所示。可以发现，在七年级前未参与数学补习的学生中，约17.8%在七、八年级间参与了数学补习；相应的英语补习比例约为13.2%；而仅有约7.5%的学生转向了语文补习。从以上可以看出，初中学生更加青睐于数学和英语补习，而对语文补习有所忽视。在学生的个人特征上，学生平均年龄约为12.5岁，男、女生各占约50%，其中约45%的学生为独生子女。在家庭背景上，父母最高教育年限平均约为11年，经济水平约为3，即一般水平。在学校特征上，大多数学校为公立学校，占比约94%；学校质量评价约为4，处于良好的水平。

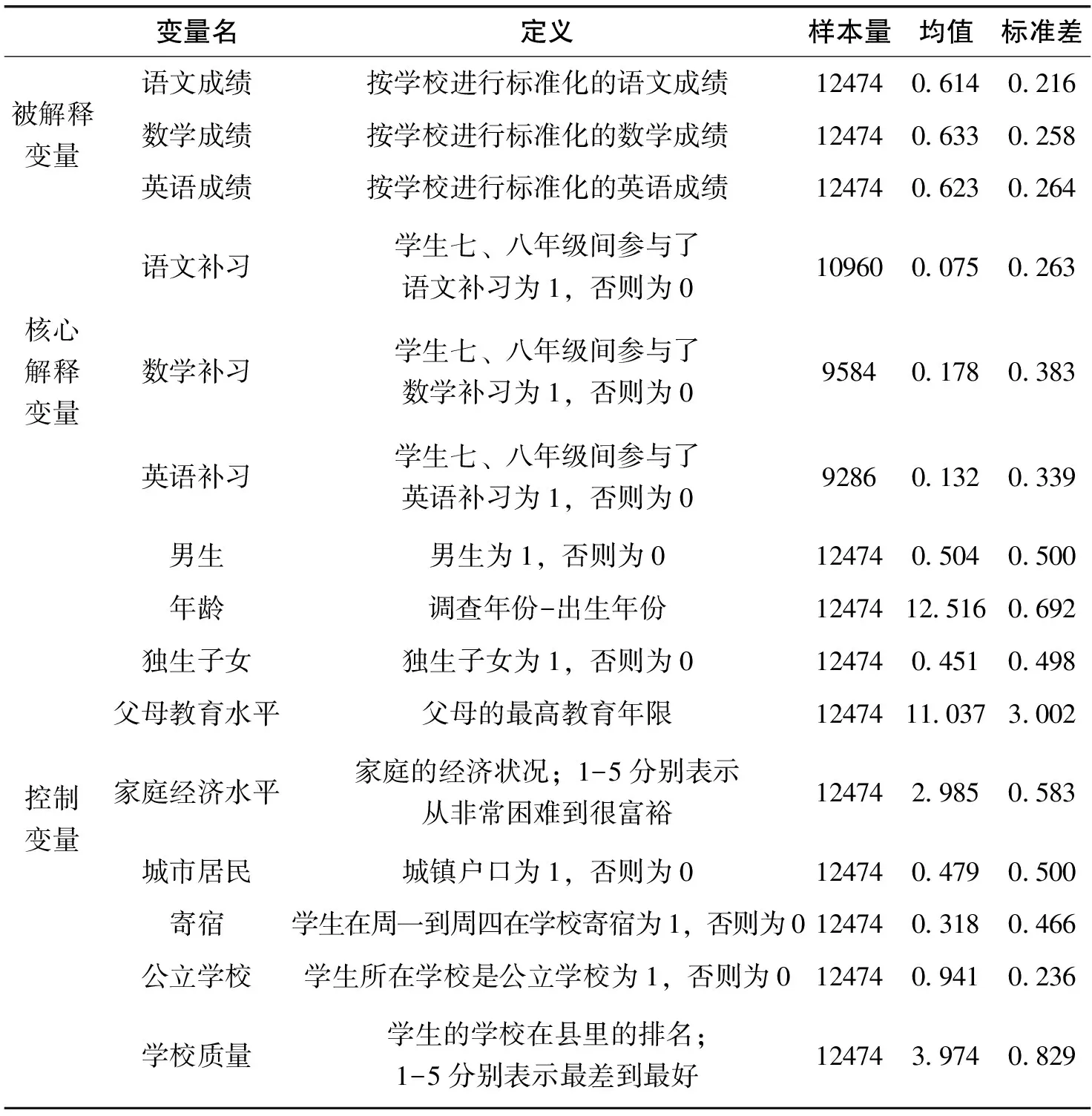
表2 变量定义与描述性统计

三、基本回归结果

(一)参与课外补习的影响因素

表3报告了学生参与语文、数学和英语补习的影响因素回归结果。系数已转化为平均边际效应。总的来看，父母教育水平、家庭经济水平和学业成绩对学生参与数学和英语补习都有着显著的正向影响。这体现出课外补习机会分配的不均衡。如果补习效应为正，则数学和英语补习可能造成学生学业成绩进一步分化。

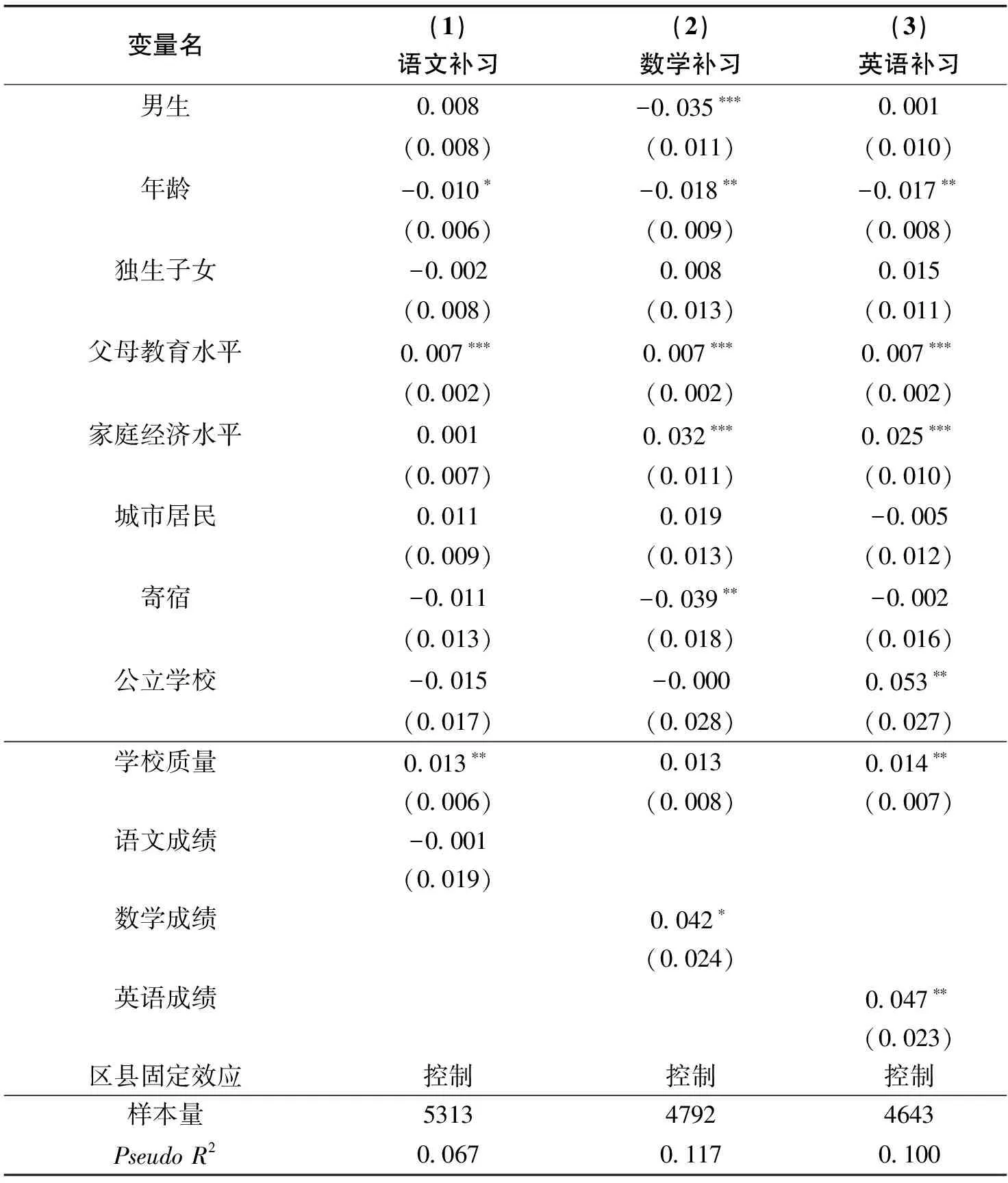
表3 参与补习的影响因素分析结果

从父母教育水平来看，其对子女选择语文、数学和英语补习都有着显著的正向影响。从家庭经济水平来看，尽管其对学生的数学和英语补习有着显著的正向影响，但是对语文补习的影响却不显著。说明经济条件优越的家庭更加重视孩子的英语和数学补习，但各经济阶层对语文补习的重视程度没有较大差异。从学业成绩来看，数学和英语成绩分别对学生选择数学和英语补习有着显著的正向影响，但是语文成绩对选择语文补习却无显著影响。这说明我国的数学和英语补习主要是“培优型”；但是语文补习未体现明显的“培优”或“补差”特征。

(二)倾向得分匹配效果检验

1.平衡性检验

在进行DID估计之前，首先使用了倾向得分匹配进行样本筛选。倾向得分匹配效果可以从协变量的平衡性及样本的共同支撑区域两个方面来考察。表4报告了基于1∶3近邻匹配后的平衡性检验结果。可以发现，所有协变量在匹配之后，处理组和对照组的标准化偏差都小于10%；t检验在0.10的水平上无法拒绝不存在组间差异的原假设；协变量联合显著性检验在0.10的水平上无法拒绝所有协变量的系数都为0的原假设。这说明倾向得分匹配很好的平衡了补习和未补习学生间的可观测性特征差异。

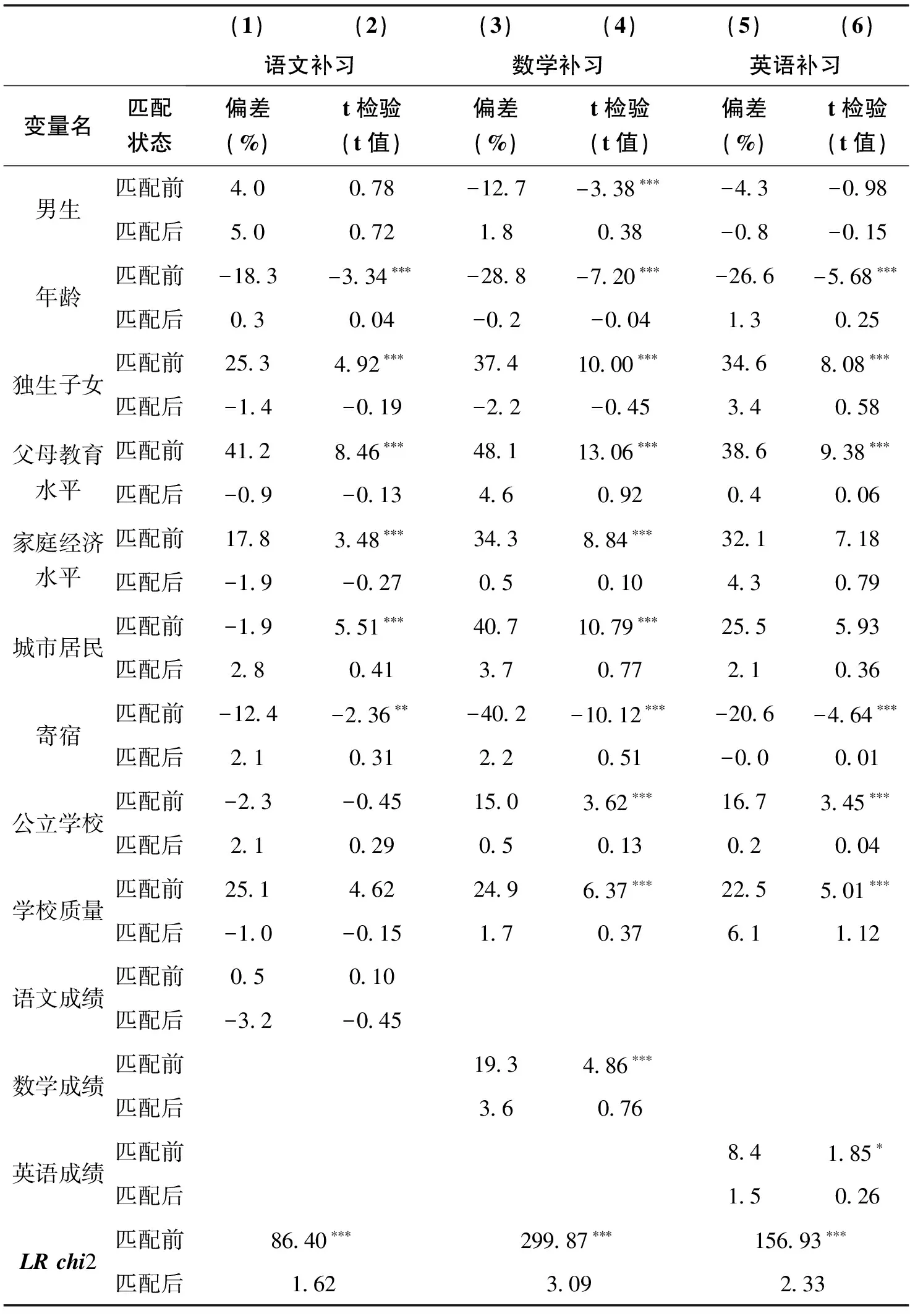
表4 倾向得分匹配效果检验结果

2.共同支撑检验

图2分别报告了涉及语文、数学和英语补习的倾向得分匹配的倾向值的共同支撑区间。可以发现，在所有的倾向得分匹配中，只有极少的样本在共同取值范围外，因此倾向得分匹配仅损失少量样本。总的来看，倾向得分匹配取得较好的效果。

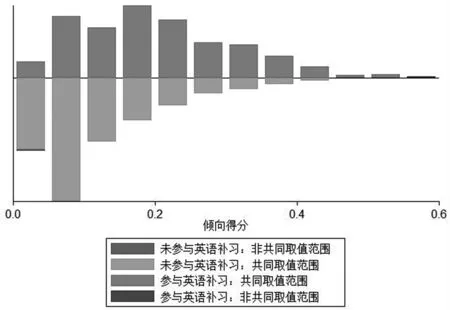
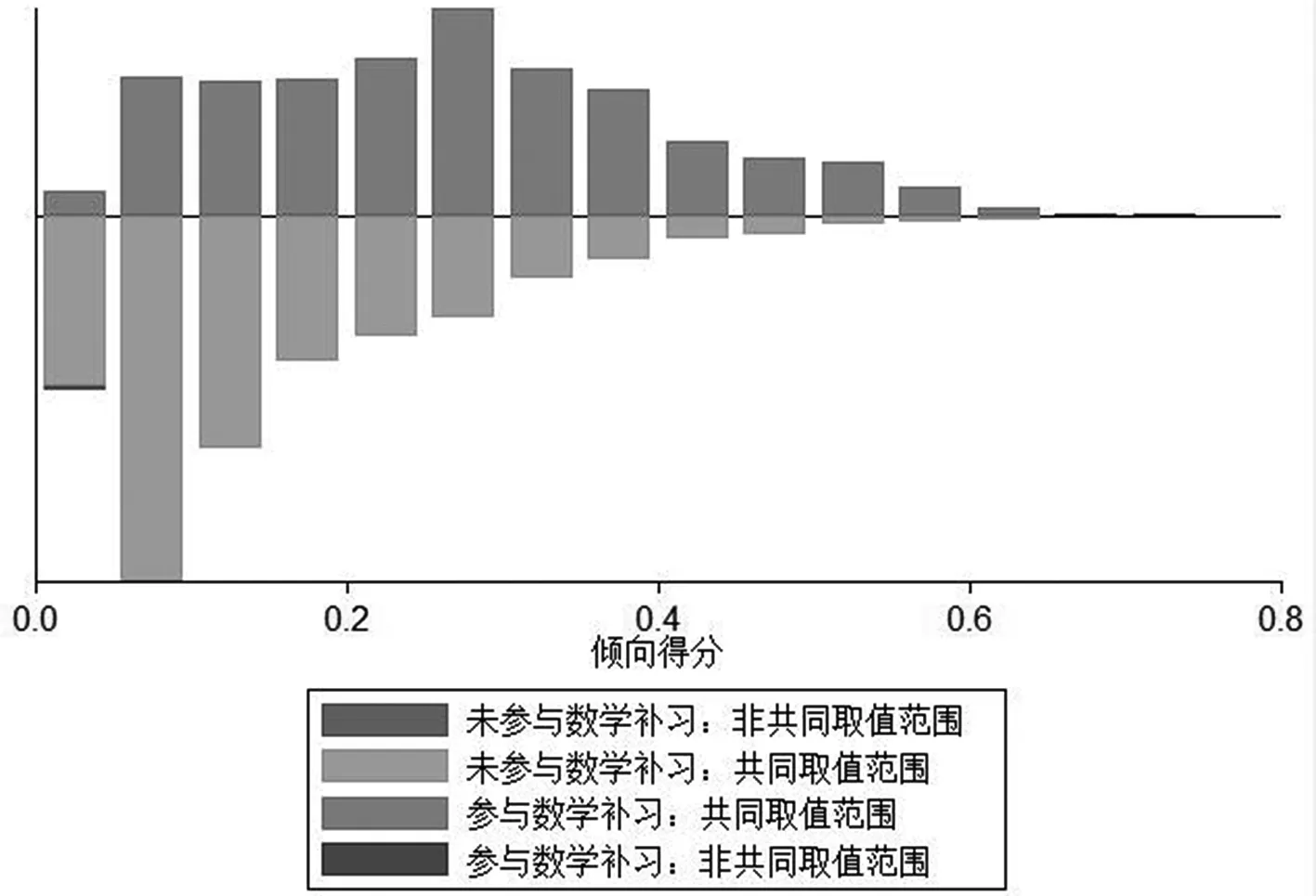
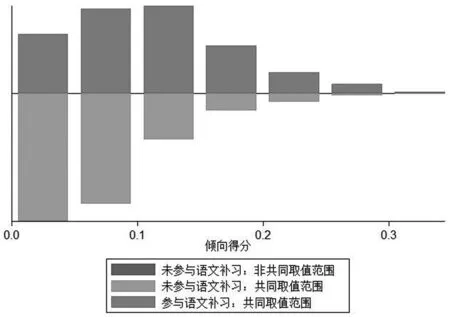
图2 倾向得分的共同取值范围

(三)课外补习对学业成绩影响的估计结果

表5分别报告了语文、数学和英语补习对相应学科成绩影响的DID和PSM-DID估计结果。总的来看，无论对于语文、数学和英语补习，两种方法的估计结果都类似，而且对相应的学业成绩都有着显著的正向影响。这说明语文、数学和英语补习都有效，与薛海平(2016)的研究结论一致。分别看来，英语补习对英语成绩的提升作用最大，使标准化成绩提升约0.05分。而语文和数学补习效应类似，都使相应标准化成绩提升约0.02分。

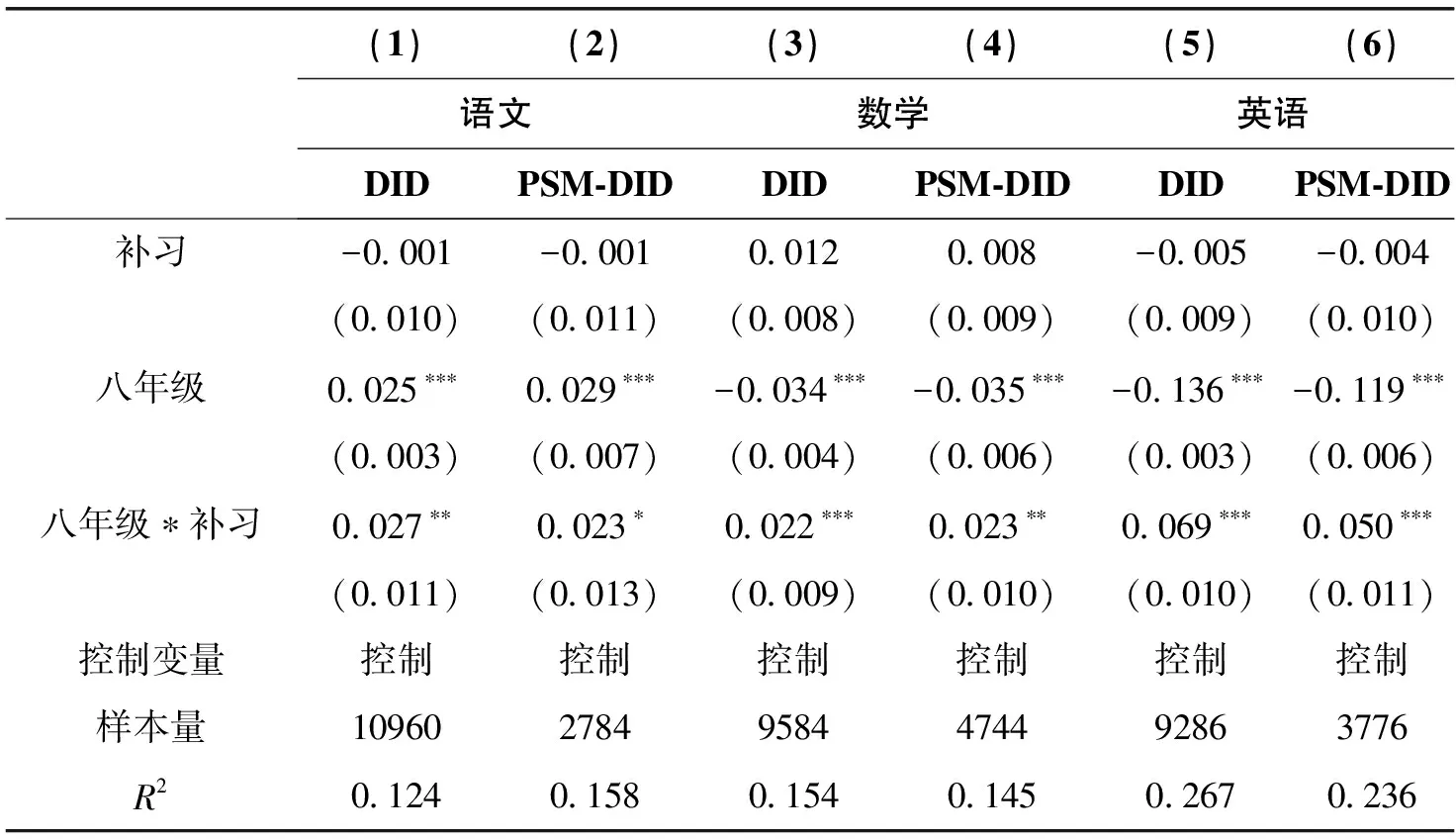
表5 课外补习对学业成绩影响的估计结果

但是部分学者使用PSM-DID方法估计得出各学科补习都无效的结论(孙伦轩和唐晶晶，2019；庞晓鹏等，2017)。这可能因为他们未将基期样本限定在未补习的学生当中。

(四)稳健性检验

这里采用不同的倾向得分匹配方法重新进行PSM-DID估计，以检验结论的稳健性。表6报告了半径匹配、核匹配和马氏匹配下的PSM-DID估计结果。可以发现，所有的交互项系数估计值与前文类似，都至少在0.10的水平上显著为正，这一定程度上说明各学科补习都有效的结论较为稳健。

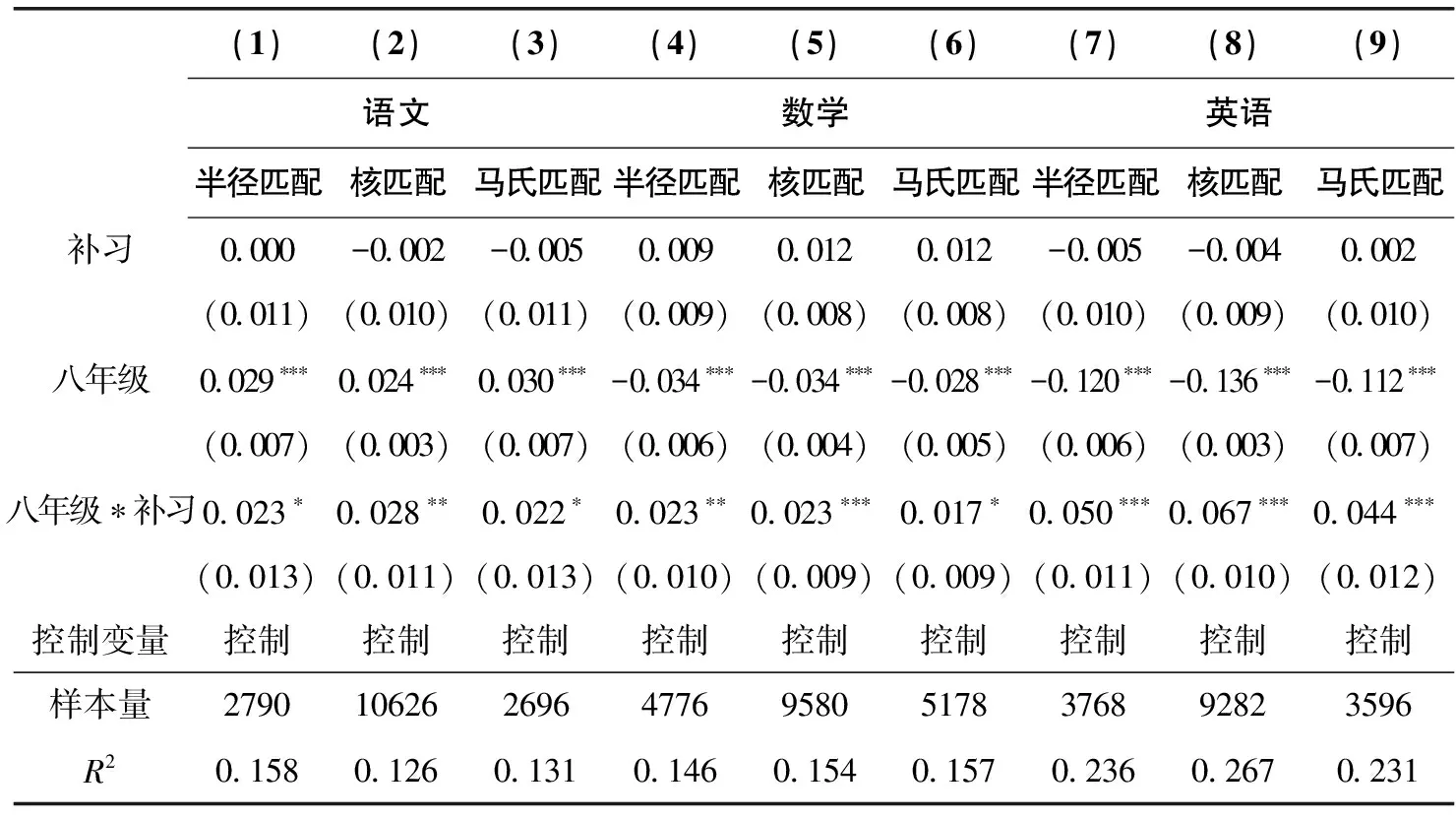
表6 稳健性检验结果

四、进一步的分析

(一)异质性分析

这里分别考察了各学科补习效应的性别、城乡、父母教育水平、家庭经济水平和原始成绩差异，表7报告了相应的估计结果。总的来看，在学生的原始成绩方面，无论对于语文、数学还是英语学科，学业成绩优异的学生的补习效应要高于学业成绩较差的学生，一定程度上说明各学科补习都会扩大学生间的成绩差异。而在性别、城乡、父母教育水平和家庭经济水平方面，并未出现某一学生群体在所有的学科补习中表现出完全的优势或劣势。例如，尽管父母教育水平高的学生的数学和英语补习效应更小，但是语文补习效应却更大。尽管家庭经济条件优越的学生的语文和数学补习效应更大，但是英语补习效应却更小。

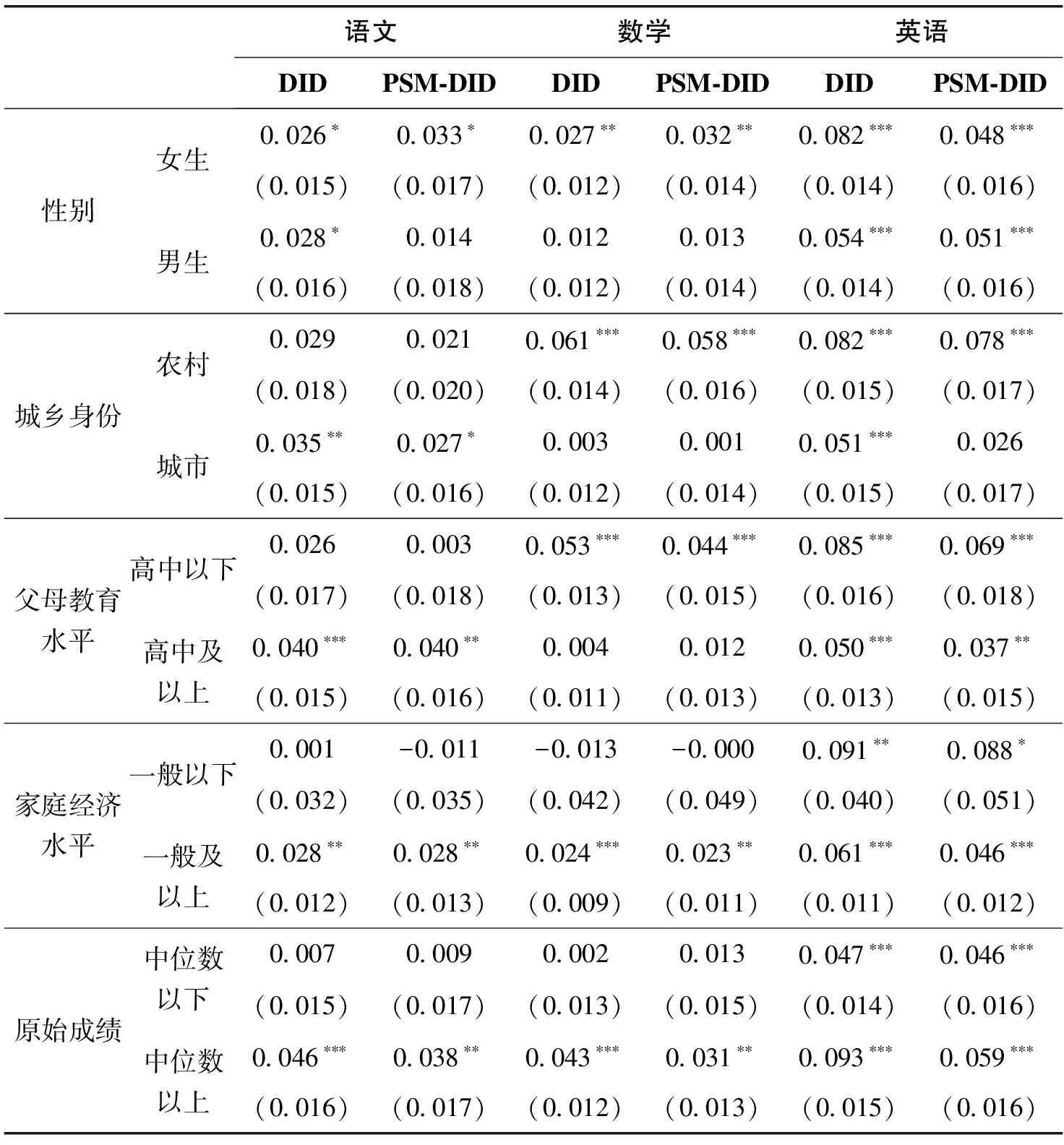
表7 异质性分析结果

从性别来看，语文、数学和英语补习对女生都有效；而对男生来说，尽管英语补习有效，但是语文和数学补习却无效。从学生的城乡身份来看，对于农村学生，数学和英语补习有效，但是语文补习却无效；而对于城镇学生，数学补习无效，语文和英语补习有着略微的效果。从父母教育水平来看，对于父母教育程度为高中以下的学生，数学和英语补习有效，而语文补习无效；而父母教育程度为高中及以上的学生，语文和英语补习有效，但是数学补习无效。从家庭经济水平来看，对家庭经济条件较差的学生，仅仅英语补习有效；但是家庭经济条件较优的学生，各学科的补习都有效。从原始分数来看，对于成绩较差的学生，仅仅英语补习有效；但是对于成绩较好的学生，各学科的补习都有效。

(二)放弃补习对学业成绩的影响

前文讨论了参与补习对学生学业成绩产生的影响。作为对照，这里考察放弃补习应该对学业成绩的影响。首先，在研究放弃某学科补习对学业成绩的影响中，将样本限定在七年级前参与此学科补习的样本中。其次，学生在七、八年级间不补习(即放弃补习)定义为1，否则为0。估计方法与前文相同，采用PSM-DID估计。

表8分别报告了相关的估计结果。总的来看，无论对于语文、数学还是英语学科，交互项的系数估计值都为负，说明放弃某学科补习对此学科的成绩有着负向影响，与前文估计的参与补习对学业成绩影响的方向相反。具体来看，放弃语文补习对语文成绩的负向影响较小，而且在0.10的水平上不显著，说明放弃语文，短期内不会降低语文成绩。而放弃数学和英语补习对相应成绩的负向影响较大，且至少都在在0.10的水平上显著。因此放弃数学和英语补习短期内会较大的降低其数学和英语成绩。

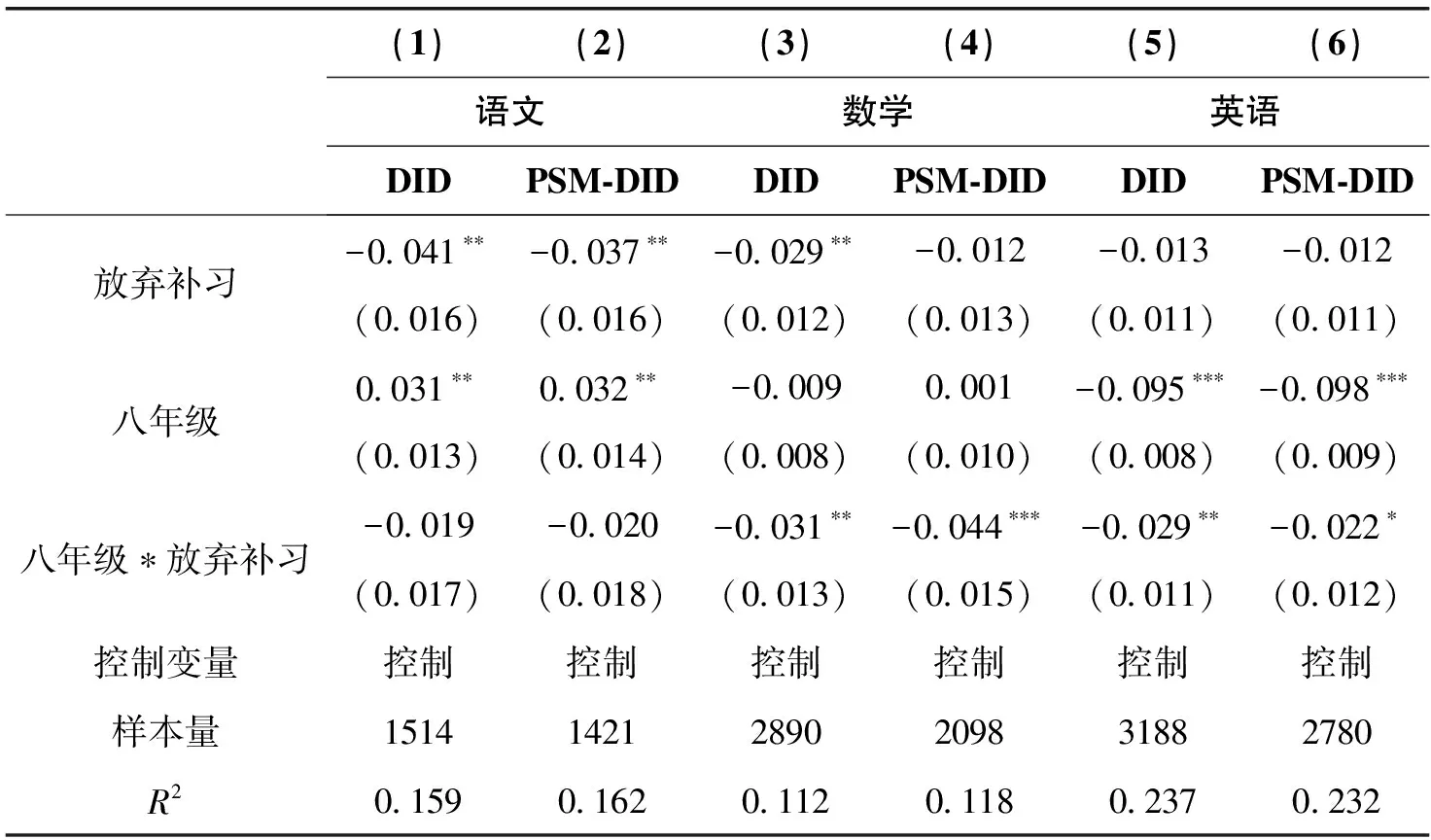
表8 放弃课外补习对学业成绩影响的估计结果

五、结论和政策建议

课外补习不仅是教育竞争的重要一环，也是教育机会不均等的重要表现。对课外补习的研究具有重要的理论和现实意义。本文基于中国教育追踪调查(CEPS)2013-2014学年基线和2014-2015学年追访调查数据，采用PSM-DID方法分别考察了初中生的语文、数学和英语补习对其相应学业成绩的影响。主要有以下发现：

从参与课外补习的影响因素来看，父母教育水平和家庭经济水平对学生参与数学和英语补习有着显著的正向影响。而尽管父母教育水平对参与子女语文补习有着正向影响，但是家庭经济水平对其参与语文补习的影响却不显著。由于家庭背景越好的学生参与数学和英语补习概率越大，说明数学和英语补习加剧了学生获得义务教育资源的不均衡，与我国政府推行的义务教育公平政策相悖。此外，我国的数学和英语补习是培优型的；但是语文补习未呈现显著的培优或补差特征。

从各学科的补习效应来看，无论对于语文、数学还是英语补习都能够显著提升相应学科的学业成绩。而且，英语补习对学生的英语成绩提升作用最大，而语文和数学补习对相应学科成绩的提升作用类似。这一结论在采用不同的倾向得分匹配方法下依然稳健。作为对照，放弃某学科的补习对此学科的学业成绩有着负向影响。

从补习效应的异质性来看，某一家庭背景的学生并未在所有的学科补习中表现出完全的优势或劣势。例如，尽管父母教育水平高的学生的数学和英语补习效应更小，但是语文补习效应却更大。尽管家庭经济条件优越的学生的语文和数学补习效应更大，但是英语补习效应却更小。此外，学业成绩优异的学生的补习效应要高于学业成绩较差的学生，这一定程度上说明各学科补习都会扩大学生间的成绩差异。

根据以上研究结论，本文提出以下两点政策建议：

其一，政府应大力支持学校开展课后服务，切实减弱学生的校外补习需求。校外补习兴起的原因很大一部分来自于学生在校学生时间的减少。在中国的“中考”和“高考”等教育制度下，学生和家长会积极利用教育资源以提升学生的学业成绩。于是，校外补习成为了多数人的选择。但是本文的研究发现，总的来看，学业成绩优异的学生更倾向于参与校外补习，而且补习效应更大。这势必造成扩大学生间的成绩差异，不利于教育的均衡化发展。因此，政府应鼓励学校开展课后服务，从而减弱学生的校外补习需求。

其二，政府应对弱势群体学生提供辅导资助，促进教育的公平和健康发展。课外补习具有一定的社会复制功能，反映了经济社会差距和社会不平等状况，是城乡差距和贫富差距的具体映像(陈全功, 2012)。本文的研究结果也发现，总的来看，家庭背景更优的学生更容易选择补习。由于各学科的补习效应都为正，因此课外补习活动会扩大不同阶层学生的成绩差距。为此，政府应该借鉴西方国家补习经验，把补习活动看作对公立教育的有益补充，向弱势群体学生提供一定的补习资助。

当然，本文的研究还存在一定的不足。尽管本文在DID估计之前，采用PSM方法平衡补习和未补习学生的可观测特征差异，以使得平行趋势假设得以满足。但是由于无法获取更多年份的追踪数据，不能对平行趋势假设进行检验。 这也可以作为进一步完善研究的方向。