考虑注浆压力的泥岩地层管片上浮特性与控制

2022-02-15贾少东马杲宇王士民姚超凡何政树

铁道标准设计 2022年2期

贾少东,马杲宇,王士民,黄兴,姚超凡,何政树

(1.南宁轨道交通集团有限责任公司,南宁 530029； 2.西南交通大学交通隧道教育部重点实验室,成都 610031)

引言

盾构在富水地层掘进过程中，管片脱出盾尾后会出现整体上浮现象，实际工程中监测到的最大上浮量超过10 cm[1]。叶飞等[2]研究发现，引起盾构隧道管片上浮的因素可分为动态因素和静态因素，前者包括盾构顶推力、注浆压力等随施工变化的荷载，后者为地下水及注浆材料产生的浮力。在施工过程中管片上浮可能导致盾构隧道出现错台、开裂、破损及管片渗漏等病害，威胁工程安全[3-5]。

针对施工过程中管片上浮的问题，国内外学者进行了大量研究，KASPER[6]建立了有限元模型，模拟在不同覆土厚度和注浆材料参数的条件下，富水地层盾构隧道的整体位移情况；季昌等[7]依托现场管片位移监测结果，分析注浆压力、千斤顶推力和浆液配比等因素对隧道上浮量的影响；朱令等[8]考虑盾构隧道的纵向拼装效应，将壁后注浆产生的压力施加在由衬砌简化成的弹性地基梁上，分析衬砌的纵向弯矩与变形量沿隧道轴线的分布情况；梁禹等[9]依托长沙市湘江大直径盾构隧道，利用梁弹簧模型计算了在上浮力作用下管片的轴力和弯矩大小；魏纲等[10]对管片施工期所受的浆液浮力数值进行了理论计算，并通过修正惯用法计算考虑上浮力情况下的管片内力；舒瑶等[11]根据同步注浆材料在围岩中的渗透效应计算浆液的凝固时间，并分析盾构纵向同步注浆作用对管片位移的影响；黄忠辉等[12]开展室内等比例试验，对整环管片施加水土压力及千斤顶顶推力，模拟管片上浮过程并记录分析了管片变形和螺栓应力。

为控制管片上浮病害对盾构隧道衬砌结构的影响，陈仁鹏等[13]利用荷载结构法，通过ABAQUS有限元软件对管片在上浮情况下的错台量进行计算，并分析减小浆液凝结时间和减小千斤顶推力对管片上浮的控制效果；戴志仁[14]研究了盾尾同步注浆材料的屈服强度对隧道抗浮性能的影响，结果表明提升注浆体的屈服强度能有效减小管片的上浮量；杨延栋等[15]在分析某硬岩地层盾构隧道上浮机理的情况下，提出采用豆砾石回填注浆和施加止水环的方式对管片上浮进行控制。

然而，现有研究通常采用荷载-结构计算法，将盾构管片衬砌简化为地基梁结构，对其施加上浮荷载，以此模拟管片的上浮情况。对于施工过程中隧道衬砌与地层、注浆材料及地下水的相互作用和管片内力分布规律的研究较少。针对以上不足，综合考虑隧道的施工过程及流固耦合效应，利用有限差分软件建立地层-浆液-结构模型，针对盾构隧道穿越水下泥岩段的施工期变形和力学特性进行研究，在此基础上进一步分析施工过程中采用速凝型注浆材料和管片堆载两种抗浮措施的效果。

1 工程概况

南宁地铁5号线旱塘站—新阳路站区间采用盾构法开挖，全长约2 101.09 m，其中，跨越邕江段长度约600 m。隧道支护结构为预制钢筋混凝土管片，其内径5.4 m，外径6 m，幅宽1.5 m，混凝土强度等级为C50。施工过程中在管片背后进行同步回填注浆。隧道穿越的地层主要为第四系和古近系地层，由上至下分别为杂填土、粉质黏土、粉土、圆砾层和泥岩，隧道区间的纵断面如图1所示。根据地勘报告和现场抽水试验结果，隧道穿越地层的物理力学参数如表1所示。施工期间受管片上浮影响，区间隧道部分管片之间出现了较为显著的错台及渗漏水问题，如图2所示。

图1 旱塘站—新阳路站纵断面

图2 管片错台及渗漏

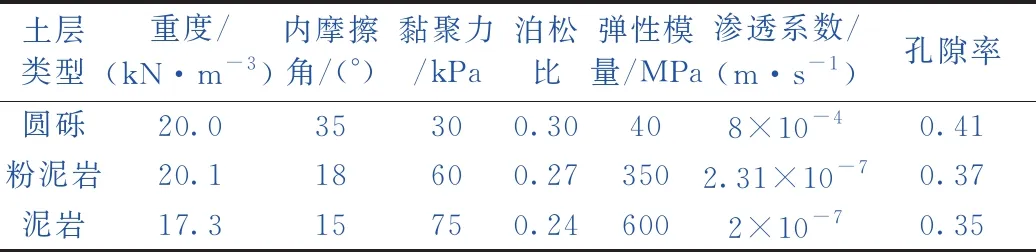
表1 地层物理力学参数

2 数值模拟

2.1 数值模型建立

现场调研结果显示，管片上浮现象最严重的区域位于上覆土层厚度最小且地下水位最高的位置。因此，选取YDK19+287.534里程断面进行管片上浮计算分析，其地质横剖面和管片横断面如图3所示。该断面隧道整体位于泥岩地层中，覆土厚9.3 m，上部水深9.13 m。管片衬砌沿环向均匀布置16个螺栓孔，纵向螺栓长36 cm，直径3.5 cm。施工过程中盾构与地层之间会形成宽15 cm的盾尾间隙，通过盾尾同步注浆进行填充，在注浆材料未凝结时，为管片上浮提供了空间。

图3 地层及管片示意(单位：m)

由于管片错台多以环间错台为主，为反映盾构隧道管片的纵向接触关系，参照文献[16]的计算方法，利用FLAC3D软件中的接触面单元对管片环间的相互作用进行模拟，以获得管片错台量和螺栓应力。环间螺栓可简化为梁单元，反映螺栓对管片错动的抑制作用。对于同一环管片而言，其环向接头的作用采用刚度折减法进行模拟，根据规范建议[17]，折减系数η取0.85。盾构隧道管片衬砌混凝土及注浆材料的取值如表2所示。

表2 支护结构材料物理力学参数

根据盾构隧道越江泥岩段地质情况，考虑模型边界对计算结果的影响，建立如图4所示的计算模型，模型尺寸定为72.0 m×30.0 m×47.9 m。模型前后边界施加纵向水平约束，左右边界施加横向水平约束，底面施加竖向约束，模型上表面为自由边界，受地层表面水体的影响，根据其上覆水头高度确定其表面的孔隙水压力为89.47 kPa。除受到地下水压力外，在注浆材料凝结前，衬砌受浆液的静态上浮力影响，浮力计算公式为

图4 盾构隧道区间数值计算模型(单位：m)

F浮=πR2ρ浆g

(1)

式中，R为管片半径；ρ浆为注浆材料的密度；g为重力加速度。经计算浆液对单位长度衬砌造成的上浮力为472.18 kN，当注浆材料凝固后上浮力随之消失。

在计算过程中，地层、管片、注浆圈和盾构机体均为实体单元。根据工程设计资料，盾构机体厚度为0.2 m，纵向长6 m。盾构隧道内部设备台车等全长约70 m，自身质量约320 t，将该荷载均匀施加在隧道管片上。

2.2 模拟方法及计算工况

为对盾构隧道施工全过程进行模拟，假设隧道周边岩土体为均质各向同性材料，在流固耦合计算时为多孔材料，流体渗流时满足达西定律，模型边界为不透水边界，开挖后的核心土单元为不透水模型；管片环间的接触为平整混凝土，不考虑凹凸榫和止水胶条等影响；忽略管片上螺栓孔和预紧力对结构力学特性的影响，并依据文献[18]的研究成果，将环间纵向螺栓等效为直螺栓。为模拟施工中管片的上浮及管片间错台，需定义环间接触形式和注浆压力。

(1)环间接触

在盾构施工过程中，不同管片环在荷载的作用下会发生相对错动，传统的耦合节点模型不能真实地反映管片衬砌的实际变形情况。因此，通过interface单元模拟不同衬砌环之间的相对错动和张开，接触面法向刚度与切向刚度的计算方法如式(2)[19]

(2)

式中，kn和ks分别为接触面单元的法向刚度与切向刚度；K为材料的体积模量；G为材料的剪切模量；Δzmin为网格的最小尺寸。计算可得kn和ks均为108.61 GPa，内摩擦角为24°，管片间接触面的黏聚力设置为0。

(2)注浆压力

注浆压力属于施工产生的一种动态上浮力，其数值大小会随注浆时间发生变化。基于张雨帆等[20]的研究成果，完全填充和部分填充浆液产生的环向注浆压力分布规律如图5(a)所示。注浆压力沿管片环向自拱顶到拱底呈线性增长趋势，当浆液未完全填充时，管片上部空间被地下水、泥浆填充，而注浆材料堆积在管片底部对隧道衬砌产生均匀分布的压力。根据盾构施工数据，隧道底部注浆压力为0.35 MPa，拱顶注浆压力约为0.20 MPa。在纵向上，同步注浆压力随盾构掘进逐渐消散。既有研究通常假设纵向注浆压力线性降低直至为0，如图5(b)所示。

图5 注浆压力分布示意

除注浆压力外，注浆材料在凝结硬化过程中，弹性模量、内摩擦角等参数也会随之发生变化。当管片脱出盾尾时，同步注浆体的弹性模量较低，是导致管片上浮的主要因素，当浆液材料凝结硬化后，其对管片的上浮力作用消失，并对管片竖向变形进行约束。因此，同步注浆材料的物理力学参数不宜设为定值。根据Talmon[21]和方勇等[22]对盾构隧道注浆固结过程中弹性模量变化的研究成果，在每环管片脱出盾尾后，将注浆材料的初始弹性模量设为0.1 MPa，之后随盾构掘进动态调整注浆材料的弹性模量等参数，令其线性增长，并在盾尾后方第4环管片位置达到定值，此时注浆压力也随之消散。越江段盾构隧道的具体开挖计算步骤如下。

(1)将盾构开挖前方地层设置为空单元，并施加盾壳结构。在盾构隧道掘进过程中，需考虑地层应力释放效应，地层应力释放系数为15%。在隧道掌子面位置施加大小为纵向不平衡力95%的反力，并固定掌子面孔隙水压力，以模拟盾构机土仓压力及刀盘顶推力，平衡开挖面位置的水土压力。

(2)在掘进完毕后激活盾尾管片，建立其与前一环管片之间的接触面，并激活盾尾后方的同步注浆层单元，在管片表面施加注浆压力及浆液浮力。室内试验结果显示，注浆材料的初凝和终凝时间分别为5 h和12 h，因此，注浆压力及浆液浮力在拼装第四环管片后消散。

(3)随开挖模拟向前推进，逐渐提高注浆材料的弹性模量，根据浆液终凝时间，注浆材料的弹性模量在脱出盾尾第四环管片位置达到设计值。在模拟过程中，假设注浆材料的弹性模量呈线性增长趋势。

(4)重复(2)、(3)步的计算过程直到开挖完成。

3 盾构施工管片上浮力学特性分析

3.1 注浆材料完全填充条件下管片上浮特性

当注浆材料完全填充时，隧道衬砌施工期竖向位移的纵向分布规律如图6所示。其中，上浮变形定义为隧道中心轴线的竖向位移量，其大小为拱顶与拱底位移的平均值。错台量为相邻两环管片轴线位移的差值。

图6 施工期衬砌位移纵向分布曲线(注浆材料完全填充工况)

由盾构开挖过程的竖向位移变化规律可知，由于盾构机的自重较大，机体上部与下部的水、土压力差仅能使盾构产生轻微上浮，其数值约为0.2 mm。受盾构壳体约束，未脱出盾尾管片的竖向变形量较小。管片脱出盾尾后，受注浆压力竖向梯度和注浆材料尚未凝结等因素影响，管片的上浮量迅速增加，竖向位移增长速率达到0.27 cm/环。当同步注浆材料终凝、注浆压力消散后，受隧道上下部水土压力差的影响，管片继续缓慢上浮，并逐渐趋于稳定，此时竖向位移增长率降低至0.012 cm/环。最大上浮量为1.97 cm，位于第20环管片处。

管片错台是沿纵向出现的环间非均匀上浮。管片脱出盾尾后，受同步注浆压力的影响产生竖向位移，而盾尾内部管片受盾构壳体约束位移较小，因此，错台量迅速增加，最大错台量为3.63 mm，随着注浆压力的消散，管片所受外部荷载逐渐转变为沿纵向均匀分布的水土压力，故错台量逐渐降低。在地铁盾构隧道中，螺栓与螺栓孔间距为1.5 mm。因此，由管片上浮引起的管片错台将导致螺栓与管片混凝土之间发生挤压，使得螺栓承担的轴力和剪力升高，并造成混凝土材料局部应力集中出现开裂和掉块等病害威胁结构安全。

3.2 注浆材料不完全填充条件下管片上浮特性

当注浆材料未完全填充时，注浆压力集中在管片下部，从而产生更大的上浮荷载。此时管片上浮量与环间错台量随开挖步的演化趋势如图7所示。

图7 施工期衬砌位移纵向分布曲线(注浆材料不完全填充工况)

受不均匀注浆压力的影响，浆液未完全填充时盾尾管片脱环后的上浮速率显著提升，其数值为0.50 cm/环，增加了72.4%。当注浆压力消散后，受水土压力差的影响，尽管管片的上浮速率逐渐降低，其竖向位移仍持续增长。由于不均匀注浆压力在竖向产生的合力增加，最大上浮量约2.70 cm，出现在注浆压力消散后的第6环位置，与浆液未完全填充工况相比最大上浮量增加了37.1%。由此可见，同步注浆压力在环向的分布特征，是影响管片施工期竖向位移的重要因素。管片的最大错台量为6.12 mm，提升了螺栓屈服与管片破损的风险。

与管片在浆液完全填充时的计算结果不同，管片在达到最大上浮量后，其竖向位移以-0.084 mm/环的速率缓慢降低。这是由于管片在注浆过程中的上浮变形量较大，而上方岩体不受注浆材料及注浆压力的约束产生沉降变形，管片后续上浮预留的空间较小，因此，管片竖向位移趋于稳定并呈现缓慢下降趋势。

4 管片抗浮措施效果分析

为控制管片上浮病害，本工程在富水地层处，采用速凝型浆液进行盾尾同步注浆，并在注浆压力未消散的位置放置混凝土管片，以抵消注浆压力和地下水产生的上浮荷载。速凝型浆液由水泥浆液和水玻璃浆液混合而成，室内实验结果表明，速凝型浆液能在数分钟至数十分钟内凝结硬化，因此，在计算中不考虑浆液对管片的浮力。速凝型注浆材料的弹性模量有所降低，其数值约为120 MPa。

4.1 压重荷载计算

在施工过程中管片堆载用于平衡竖向注浆压力及孔隙水压力差产生的上浮力，单位长度上注浆压力产生的上浮荷载如式(3)

(3)

式中，θ为管片外部节点与竖直方向的夹角；P1为管片上部注浆压力；R为管片外径；k为注浆压力在竖向的梯度。由式(3)可知，单位长度注浆压力产生的上浮力为235.50 kN。

单位长度上地下水引起的浮力与前文所述浆液浮力的计算方法类似，其数值为276.95 kN。单位长度管片的自重荷载约为177.26 kN。因此，为平衡多余的上浮力，每延米需约1.9环管片。在实际工程中管片自重荷载通过电瓶车和临时轨道作用在混凝土衬砌上，受现场环境限制，每辆电瓶车最多运送1环管片，考虑电瓶车自身质量，堆载产生的荷载约为83.23 kN/m。在数值模拟过程中可简化为作用在管片内部的2组对称分布的线性荷载，管片堆载方式如图8所示。

图8 管片堆载控制示意

4.2 抗浮措施对隧道上浮量的影响

采取速凝型浆液和管片堆载等抗浮措施后隧道衬砌的竖向位移及管片错台量如图9所示。

图9 施工期衬砌位移纵向分布曲线及管片错台量(采取抗浮措施工况)

当采用抗浮措施时，隧道衬砌的竖向位移显著降低，最大上浮量仅为1.31 cm，与浆液未完全填充和完全填充的工况相比分别降低了51.48%和33.50%。受管片堆载的影响盾尾脱环后隧道的上浮变形受到限制，随着注浆压力的逐渐消散，管片竖向位移增长率进一步降低，盾尾脱环段的位移增长率约为0.11 cm/环。当管片堆载移除后，受地下水浮力等因素影响，管片竖向位移增长率有所提升，随后不断下降直至竖向位移趋于平衡。

由图9(b)可知，采取抗浮措施后，管片纵向错台曲线有2个极大值点，这是由于移除管片堆载后管片在水土压力差下产生的上浮所导致的。管片之间的最大错台量位于盾尾脱环位置，其数值为1.56 mm，与前述2种工况相比分别降低了74.51%和57.02%，仅略大于螺栓与管片之间的预留间隙，有效地提升了螺栓与管片混凝土的安全性能。由计算结果可知，将管片堆载施加在注浆压力未消散段，可以有效减小管片在上浮速率最快时期产生的变形，而后续上浮变形仅由地下水浮力和土压力差引起，受上覆土压力的影响该变形较小。此外，速凝型浆液能够消除注浆材料引起的静态上浮力，对管片的上浮起到了约束作用。

4.3 抗浮措施对隧道内力的影响

受注浆压力、孔隙水压力等荷载的影响，隧道衬砌在上浮过程中竖向位移大于水平位移，衬砌整体呈横椭圆形。提取衬砌内部应力，计算模型中间断面管片的内力。断面轴力定义受压为负，弯矩内侧受拉为正。3组计算工况的内力环向分布规律如图10所示。

图10 管片的内力雷达图

3种工况下衬砌轴力和弯矩的分布规律大致相同。隧道拱顶和拱腰位置的轴力较大，受注浆压力和水压力影响拱底位置轴力减小，弯矩增大，管片不同位置的轴力分布不均匀。3种工况下管片最大轴力分别为2 647.12，2 263.23，1 645.44 kN(受压)，均位于拱腰位置。当采取抗浮措施时，管片最大轴力与前2组工况相比，分别降低了37.84%和27.30%。

受底部上浮力和隧道顶部围岩及注浆材料约束作用的影响，隧道拱顶和拱底位置出现正弯矩，负弯矩主要位于拱腰位置。3种工况最大负弯矩分别为97.47，77.71，26.22 kN·m，最大正弯矩分别为67.27，48.06，5.96 kN·m。由此可见，衬砌弯矩在数值上显著降低，且最大正、负弯矩的差值由164.74 kN·m减小为32.18 kN·m。因此，当采用管片堆载和速凝型浆液作为抗浮措施时，隧道衬砌内力降低，且沿环向的分布更加均匀，有效减小了衬砌发生局部破坏的风险。

4.4 抗浮措施对螺栓轴力的影响

各环管片螺栓的最大轴力沿纵向分布情况如图11所示，螺栓受拉时轴力为正值。

图11 螺栓最大轴力分布曲线

由图11可知，螺栓最大轴力与管片错台量沿纵向的变化规律类似，纵向螺栓轴力最大值均出现在错台量较大的位置。管片脱离盾尾脱后螺栓轴力迅速增加。当不采取抗浮措施时，螺栓轴力在注浆压力消散前后达到最大值；采取抗浮措施时，由于管片堆载移除后，管片错台量二次增长，螺栓最大轴力随之继续增加，随后逐渐下降，螺栓轴力的最大值出现在第12环位置。3组工况下螺栓的最大轴力依次为372.86，217.87，106.61 kN。未采取抗浮措施2种工况最大轴力为采取抗浮措施后的螺栓最大轴力的3.50倍和2.04倍。