大坡道米轨道床阻力及轨排稳定性研究
2022-02-15韩义涛田春香张沐然
韩义涛,田春香,张沐然,韦 凯
(1.中铁二院工程集团有限责任公司,成都 610031; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
引言
我国西部地区正在修建穿越山区的某米轨铁路,该线路全线铺设为有砟轨道无缝线路。与其他地区不同的是,该线路运行于艰险山区,不可避免地存在一些坡度极大的路段,其最大坡度甚至达到了250‰。为解决大坡道地段米轨列车爬行困难的问题,通常采用列车齿轮与轨道齿条的啮合作用来提供牵引力[1-3]。米轨铁路在大坡道地段设置齿轨,因此在荷载作用下其受力方式与传统轨道结构完全不同。然而,目前国内没有如此大坡道有砟轨道的先例,国际范围内也没有规范和相关研究为其提供理论支撑,为判别大坡道米轨(齿轨)有砟轨道建设的可行性,为其设计提供理论指导,有必要对大坡道米轨(齿轨)有砟轨道道床阻力及轨排结构稳定性进行理论和试验研究。
近年来,许多学者利用离散元方法对有砟轨道进行研究。KHATIBI F等[4]利用PFC建立了三维实体离散元模型对一种特定混凝土轨枕的道床横向阻力进行了数值模拟,同时研究了道床厚度、道床肩宽和砟肩堆高对道床阻力的影响。以上研究利用试验及数值仿真的方法,对水平路段标准轨距混凝土枕的道床阻力进行了分析,得到用于标准轨距混凝土枕道床阻力参数及影响因素,为有砟轨道离散元的研究提供了方法和经验;李粮余等[5]利用有限元法对山地米轨轨道结构稳定性展开了研究,通过有限元强度折减法对有砟道床的整体稳定性进行分析。但文中将有砟道床考虑为连续介质,无法考虑有砟道床的离散特性,并不能准确地模拟有砟道床的力学特性。
鉴于此,利用离散元和有限元法对大坡道米轨(齿轨)有砟轨道结构稳定性进行分析。首先,通过室内阻力试验及仿真分析验证两种模型的正确性;之后通过改变模型的坡度,计算不同坡度条件下的道床阻力,分析坡度对米轨铁路混凝土轨枕道床纵、横向阻力的影响;最后,对荷载作用下大坡道米轨(齿轨)有砟轨道结构纵、横向稳定性进行分析,综合考虑轨排和道床的稳定性,给出坡度极限值及曲线段允许的最小半径值。
1 米轨有砟轨道模型
1.1 轨道结构离散元模型
利用PFC离散元软件建立了钢轨-扣件-轨枕-道砟离散元模型,模型整体如图1所示。

图1 米轨轨排结构离散元模型
模型中钢轨采用50 kg/m钢轨,轨枕采用米轨混凝土枕,枕间距为60 cm,扣件纵向阻力取为11 kN/组、横向阻力取为7.8 kN/组,在PFC离散元模型中表现为钢轨与轨枕之间的非线性接触。钢轨和轨枕皆为真实廓形,选用clump簇颗粒来模拟,簇内部用球颗粒填充。有砟道床严格采用一级道砟过筛率来执行,道砟用球颗粒模拟。模型中,枕下道床厚0.25 m,道床顶面宽3 m,道床边坡坡度1∶1.75,所有参数与室内试验模型保持一致。米轨混凝土轨枕有砟道床离散元模型建立时,采用自然沉降法将颗粒填充在道床模型范围内,静置一段时间之后,利用墙体对其进行压实,使有砟道床密实度满足要求。模型前后两端利用墙体单元模拟边界。
模型中道砟、轨枕、墙体各项参数如表1所示[6-12]。

表1 道床离散元参数取值
1.2 轨排结构有限元模型
有限元模型中,将钢轨和轨枕简化为梁结构,将扣件和道床的作用简化为有横向刚度、纵向刚度、垂向刚度和扭转刚度的弹簧单元。该模型的受力和传力途径为:钢轨将列车和温度荷载作用通过扣件弹簧传递到轨枕,轨枕通过道床弹簧单元传递到路基上,假定路基为固定,简化力学模型如图2所示。

图2 米轨轨排结构有限元模型
2 模型验证
2.1 离散元模型验证
为验证离散元模型和参数的正确性,进行米轨混凝土枕道床阻力室内试验与数值模拟试验,在模型尺寸完全一致的情况下,利用米轨有砟轨道离散元模型进行水平条件下道床纵、横向阻力数值仿真模拟,并与相同条件的现场试验结果进行对比验证[13-15]。
2.1.1 道床阻力测试试验
在室内铺设了米轨有砟轨道原比例试验模型,钢轨采用50 kg/m钢轨,轨枕采用米轨混凝土枕,间距为60 cm,枕下道床厚0.25 m,道床顶面宽3 m,道床边坡坡度1∶1.75,道砟为一级道砟。道砟分层铺设,每一层铺好之后用夯实机进行夯实,整个轨道结构铺设完成后,再用道砟振捣器进行振捣,以此保证有砟道床的密实程度。试验模型与仿真模型条件完全相同,试验现场及装置如图3所示。

图3 米轨混凝土轨枕阻力测试
采用单根轨枕测试法进行道床纵、横向阻力测试试验[11],拆除每次测试的轨枕上所有扣件系统。测试道床纵向阻力时,利用带有扣件系统的邻枕提供反力,测试横向阻力时利用钢轨提供反力。道床纵、横向阻力各测试20组,记录每组轨枕位移与对应的道床阻力。计算各个位移对应的道床纵、横向阻力平均值,得到道床纵、横向阻力与轨枕位移的关系。
2.1.2 数值模拟及验证
数值仿真时也采用单根轨枕测试法测试其道床纵、横向阻力,首先解除第3根轨枕与两根钢轨之间的非线性接触;然后对轨枕簇单元施加一个很小的速度使之产生位移,记录位移过程中轨枕簇所受纵向接触力与对应的位移,即可得到道床阻力-位移关系。将试验与仿真的纵、横向阻力与位移的关系进行对比,如图4、图5所示。

图4 道床纵向阻力测试值与仿真值

图5 道床横向阻力测试值与仿真值
由图4、图5可知,PFC数值仿真模拟所得到的道床纵、横向阻力与实测值趋势相同,数值相近,能正确反映道床阻力-轨枕位移之间的关系。因此,离散元模型及参数符合实际,可用此模型进行米轨混凝土枕道床阻力及稳定性研究。
2.2 有限元模型的验证
为验证米轨轨排结构有限元模型的正确性,对两种模型的轨排结构施加相同的纵向荷载,对比离散元方法和有限元方法仿真得到的轨排结构纵向位移,从而达到相互验证的目的。为确保模型验证的有效性,有限元模型和离散元模型的规模和约束保持一致,模型共6根轨枕,钢轨两端为自由端。
在离散元模型和有限元模型的两根钢轨均施加纵向的均布荷载,荷载值从0开始加载至80 kN,加载过程中提取各钢轨和轨枕的位移。轨排结构位移与荷载大小的关系如图6、图7所示。

图6 钢轨位移变化曲线
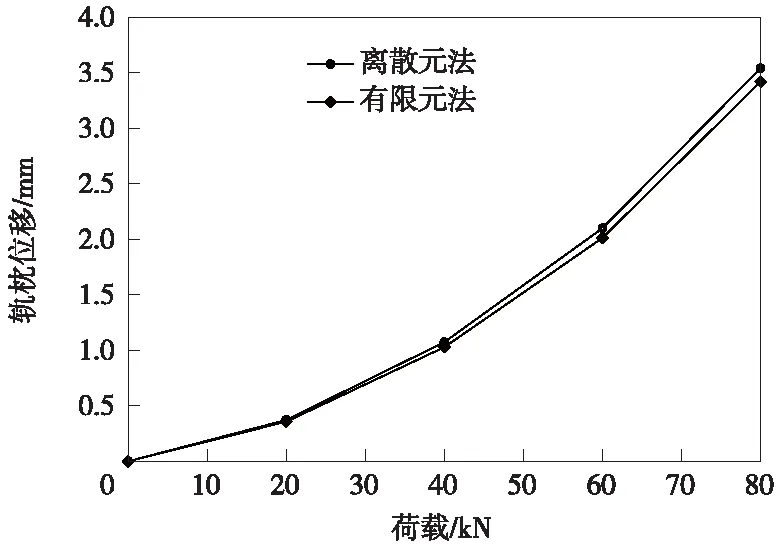
图7 轨枕位移变化曲线
由图6、图7可以看出,有限元法和离散元法计算得到的轨排结构位移趋势相同,数值接近。为提高计算效率,在已知道床阻力参数的条件下可用有限元法研究轨排结构稳定性。
3 坡度对米轨道床阻力的影响
在不同坡度条件下,轨道结构与重力方向的角度不同,导致轨道结构的力学性能有所差异。当坡度改变时,轨枕与有砟道床的接触与传力方式会发生改变,同时由于道床内碎石道砟的排列和传力方式也会发生改变,散粒体道床自身的力学性能也会发生变化。因此,坡度会对有砟轨道的道床阻力产生一定影响,进而影响轨排结构的稳定性。
为研究坡度对米轨混凝土枕道床纵、横向阻力的影响,改变离散元模型的坡度,研究不同坡度下米轨混凝土枕道床阻力与轨枕位移的关系。
通过PFC数值模拟得到不同坡度情况下米轨混凝轨枕的道床纵、横向阻力数值仿真结果,如图8、图9所示。

图8 不同坡度道床纵向阻力-位移关系

图9 不同坡度道床横向阻力-位移关系
从图8、图9可以看出,米轨混凝土枕道床纵、横向阻力随坡度增大而减小。在坡度较小时,道床阻力减弱较小,随着坡度增大,道床纵、横向阻力降低越来越明显。
不同坡度条件下道床纵、横向阻力设计值(位移2 mm对应的道床阻力值)见表2。
我国目前在建米轨铁路最大坡道为250‰,由表2可知,当坡度为250‰时,米轨混凝土枕的道床纵、横向阻力分别为12.30 kN/枕和9.95 kN/枕,分别比水平条件下减小5.7%和4.5%,减弱幅度较小。
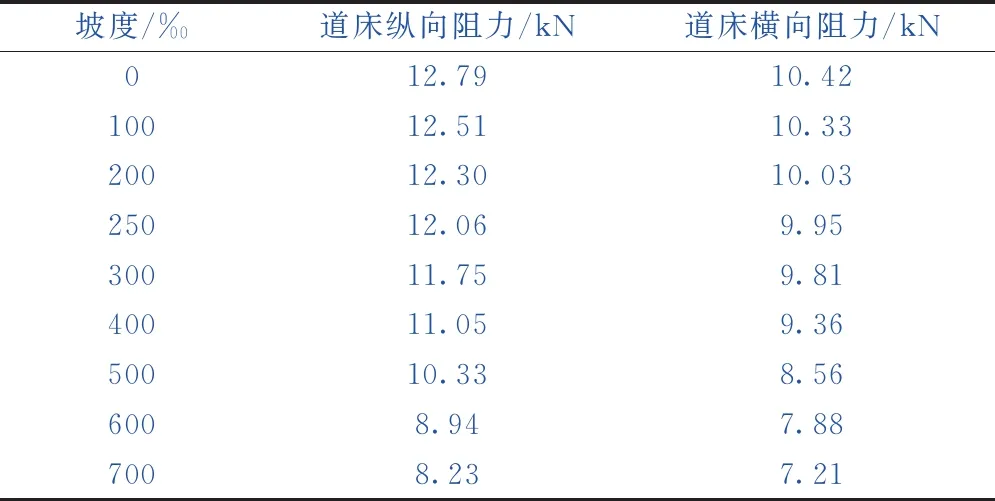
表2 不同坡度道床阻力设计值
图10为不同坡度下米轨混凝土枕道床纵、横向阻力设计值与无坡度条件下道床阻力的比值与坡度余弦值的对比关系。如有砟道床保持稳定,则坡道上轨枕的道床阻力值与水平段道床阻力的比值近似于坡度的余弦值。
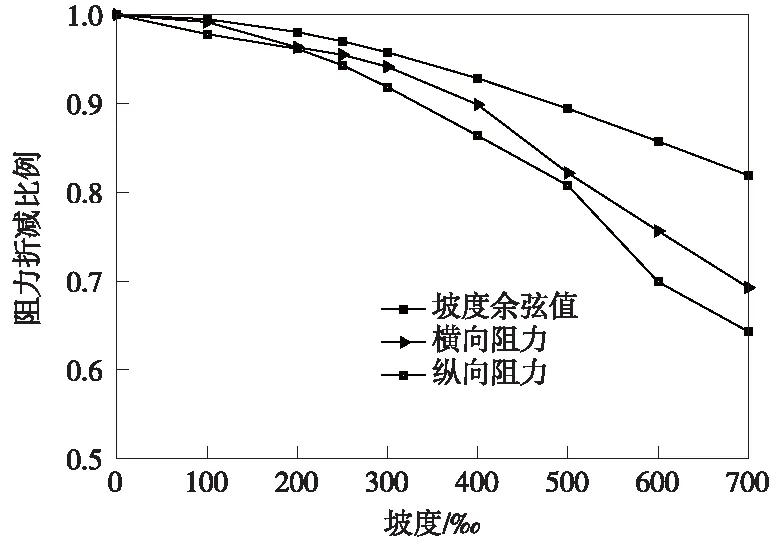
图10 道床纵、横向阻力折减比例
由图10可知,不同坡度下道床阻力与水平条件下道床阻力的比例小于坡度对应的余弦值,且随着坡度增大,二者相差越来越大。在有坡度的情况下,导致道床阻力降低的原因有两个方面:其一,轨枕与道床之间的正压力值小于轨枕自身的重力;其二,在坡道上道砟颗粒之间的接触力降低,导致有砟道床结构整体稳定性减弱。因此,道床坡道条件下道床阻力并不能简单地按照坡度余弦值进行折减,应通过试验或数值模拟进行取值。
4 轨排结构稳定性分析
离散元法计算效率偏低且很难模拟较大的模型,为尽可能避免边界效应的影响,在已知道床阻力参数后,利用有限元法建立轨排结构有限元模型,进行不同坡度条件下米轨(齿轨)轨排结构的稳定性分析。
4.1 纵向稳定性分析
以某在建山地米轨铁路为例进行分析,米轨列车轴重分配示意如图11所示。

图11 米轨列车轴重示意(单位:m)
在大坡道地段列车在齿轨段启动或制动时考虑齿条啮合及轮轨摩擦的影响,最不利工况为列车减速制动过程,此时作用在齿轨以及轨枕上的力最大,包括列车重力沿坡度方向的分力和列车制动加速度产生的惯性力,即
F齿轨=Gsinθ+ma
(1)
式中,a为米轨列车最大制动加速度,取1.2 m/s2;计算时将齿轨所受的力换算为均布荷载,均匀施加在轨枕与齿轨连接处进行计算。为消除边界效应的影响,设置模型长度400 m(钢轨),钢轨两端无约束。
为得出米轨有砟轨道的坡度极限值,对0~600‰坡度范围内的轨道结构纵向稳定性进行分析。通过对有限元轨排模型施加列车荷载,计算不同坡度条件下的轨枕位移值。500‰坡度施加荷载后的轨枕位移云图如图12所示。

图12 轨枕位移云图(坡度为500‰)
经计算,不同坡度条件下轨枕纵向位移值见表3,轨枕纵向位移与坡度间的关系如图13所示。

表3 不同坡度下轨枕纵向位移
由图13可知,随着坡度增大,轨枕位移显著增大,当坡度为600‰时,轨枕位移超过2 mm,达到2.32 mm,此时轨枕的纵向位移较大,轨排结构易出现失稳现象。因此,轨排稳定性建议最大坡度不超过500‰。

图13 轨枕纵向位移-坡度关系曲线
图14为坡度600‰时列车制动荷载作用下道砟颗粒位移云图。从图14可知,轨枕附近道砟颗粒位移较大,最大位移值达3.06 mm;轨枕间道砟颗粒位移较小,最大位移值为1.2 mm;砟肩附近道砟颗粒位移小,最大位移为0.75 mm。在外加纵向荷载的作用下,有砟道床失稳的临界坡度将小于自然休止角。但当坡度为700‰时,施加列车荷载后道砟颗粒始终会产生位移,且不平衡力与平均接触力比值始终>0.01,离散元模拟无法达到平衡状态,此时有砟道床结构已无法保持稳定,因此,要保持有砟道床结构整体稳定,最大坡度应≯600‰。

图14 道砟颗粒位移云图
综合考虑轨排结构和有砟道床的整体稳定性,建议米轨有砟轨道最大坡度不超过500‰。
4.2 横向稳定性分析
在曲线段,当钢轨温度升高时,钢轨内部产生较大压力,使得钢轨向外膨胀,产生横向位移,当横向位移过大时,将会影响轨道结构和行车的安全性[16-19]。而由于大坡道段道床横向阻力有明显减弱,轨道框架的稳定性面临严峻挑战。因此,必须对其进行研究,以确定安全的曲线半径。
为考虑齿轨的影响,本节计算考虑了以下两种工况:工况1,无齿轨;工况2,有齿轨且齿轨做有缝处理。对轨道结构进行温升处理,取轨枕2 mm时的升温幅值为线路的允许温升,得出不同坡度下曲线半径和允许升温的关系曲线,如图15、图16所示。

图15 不同坡度曲线半径-允许升温关系曲线(工况1)

图16 不同坡度曲线半径-允许升温关系曲线(工况2)
从图15、图16可以看出,齿轨对于轨排结构横向稳定性有一定影响。当轨排存在齿轨且齿轨做有缝处理时,其自身的抗弯性能增强了轨排结构的稳定性,钢轨允许温升增大,对于轨排结构横向稳定性是有利的。
根据我国在建米轨铁路当地的情况,设计锁定轨温为6.7~16.7 ℃,当地最高轨温为48 ℃,最大升温幅度可达到41.3 ℃。对于长大坡道地段,考虑列车频繁制动或牵引,钢轨温度会明显升高,故在最高轨温基础上再增加10 ℃进行无缝线路检算[20]。综上,为保持轨道结构稳定,在最大坡度为250‰情况下,该工程无齿轨段曲线半径应≮700 m;齿轨段曲线半径≮600 m;若遇特殊情况需要设置更小的半径,则需采取增加道床阻力的措施。
5 结论
在建立米轨有砟轨道离散元和有限元模型并验证了两种模型的正确性后,通过改变离散元模型坡度,分析了其道床阻力的变化趋势;且分析了不同坡度条件下米轨(齿轨)轨排结构的稳定性,得出以下结论。
(1)受轨枕与道床之间正压力减小和道砟颗粒之间接触减弱的共同作用,随着坡度增大,米轨混凝土枕道床纵、横向阻力逐渐降低,且导致道床减弱幅度明显高于轨枕与道床的正压力降低幅度。
(2)当坡度为600‰时,轨枕位移超过2 mm,轨排结构容易出现失稳现象;当坡度为700‰时,有砟道床整体结构已无法保持稳定。综合考虑轨排结构和有砟道床整体稳定性情况,建议米轨有砟轨道最大坡度不超过500‰。
(3)综合考虑温度荷载及列车制动荷载,建议在250‰的坡度下,无齿轨段曲线半径≮700 m,有齿轨段曲线半径≮600 m。若遇特殊情况需设置更小的半径,则需采取增加道床阻力的措施。
