波浪入射角度和周期对系泊船舶运动影响的数值模拟研究
2022-02-15袁治巍柳淑学李金宣张昊宸
袁治巍,柳淑学,李金宣,张昊宸
(大连理工大学,海岸和近海工程国家重点实验室,辽宁 大连 116024)
近些年来,随着近岸深水岸线的减少以及船舶大型化的发展,港口建设向外海深水区延伸[1],大型的开敞式码头建设比例逐步增加。开敞式码头离岸较远、水深偏大、无防波堤掩护,所在水域存在较为复杂的波浪场,影响船舶作业。因此,现阶段在研究开敞式码头前系泊船泊稳问题时,要考虑周期较长波浪、波浪的入射方向与波浪谱的特性等方面的影响。
系泊船的运动量是衡量泊稳的重要指标,而系泊船的运动响应问题是复杂耦合系统的动力响应问题[2]。近些年来,众多学者对波浪作用下系泊船的运动特性展开深入研究,沈雨生等[3]通过研究揭示了横摇运动量随着波浪谱峰周期的增大先增大后减小、在波浪谱峰周期接近船舶横摇固有周期时产生峰值的规律;史宪莹等[4]的研究表明,当混合浪的能量一定时,低频波浪成分能量越大,系泊船的运动量一般也越大;马小剑等[5]的数值计算结果表明,系泊船横移运动量呈现随波浪群高的增大而增大的趋势。迄今为止,在研究波浪作用下的系泊船运动响应问题已有较多成果,但是这些研究大多考虑横浪作用,而实际工程中开敞式码头水域的波浪周期范围较大,且波浪的方向分布较广,须进一步研究不同周期与入射角度的不规则波浪的作用对船舶运动量的影响。目前,各机构开发的如OPTIMOOR、MOSES、Ship-mooring等系泊分析软件得到了广泛的应用,在工程计算中能取得较为可靠的结果[6-8]。
本文基于MIKE 21 Mooring Analysis 软件,建立一艘30万t油船的系泊数值模型,研究不同周期和入射角度波浪作用下系泊船舶的运动特性。
1 计算方法
MIKE 21 Mooring Analysis是一款动力系泊分析软件,可计算港口内复杂海洋环境下系泊船舶的运动问题[9]。软件基于势流理论,采用间接时域法,通过边界元方法计算频域下系泊船水动力系数,再通过傅里叶变换方法将频域参数转换到时域中,求解船舶运动方程。此外,考虑浅水中波浪的非线性影响,采用改进的Boussinesq理论计算入射波浪的波浪场[10]:
Cijxj(t)=Fwj(t)+Fej(t)
(1)
式中:Mij为惯性恢复力矩阵;Cij为静水恢复力矩阵;Kij为迟滞函数矩阵;t为时间;τ为迟滞时间;mij为船体附加水体质量矩阵;Fej为缆绳护舷等引起的作用力矩阵;Fwj为波浪激振力矩阵,采用Bingham方法计算[11];xj为笛卡尔坐标系下浮体六自由度运动矩阵。
2 数值模拟船舶模型条件
本文考虑30万吨级油码头,如图1所示。平面布置形式为开敞式蝶形布置,码头及系缆墩结构形式为桩基结构。泊位长度394 m,码头面、靠船墩及系缆墩顶高程6.5 m,设计高水位为2.5 m,码头前沿底高程为-23.7 m。30万t油船主要参数为:总长334 m,型宽60 m,型深31.2 m,满载吃水22.5 m,重心高20.6 m,排水量34.565 5万t,横摇周期17.87 s,纵摇周期13.62 s。
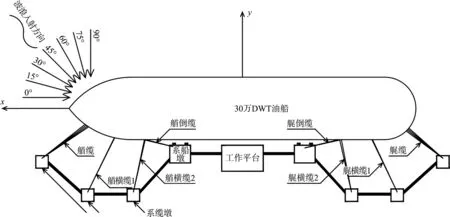
图1 码头平面布置及系缆方式
船舶系泊缆绳的布置采用4:2:2:2(艏/艉缆:横缆1:横缆2:倒缆)方式,共计20根。缆绳采用直径75 mm尼龙绳,初张力为100 kN。缆绳受力和变形关系按Wilson公式计算:
T=Ced2(Δs/s)n
(2)
式中:T为模型缆绳的拉力;Ce为尼龙缆绳弹性系数,取15.4 GPa;d为缆绳直径;n为系数,对于尼龙缆取3.0;s为缆绳长度;Δs为缆绳伸长度。
护舷采用SC3000H标准反力型一鼓一板橡胶护舷,四点靠泊。设计压缩相对变形47.5%时,最大吸能量为5 100 kJ,设计反力为4.4 MN。
3 数值模型的建立与验证
3.1 模型的建立
采用数值方法研究不同周期和入射方向波浪作用下系泊船舶的运动响应,首先通过物理模型试验验证数值模型的有效性。物理模型试验在大连理工大学海岸和近海工程国家重点实验室的多功能综合水池中进行。模型采用重力相似准则,比尺为1:60。缆绳和护舷的受力-变形模拟结果见图2。

图2 缆绳和护舷模拟曲线对比
3.2 模型验证


表1 数值模型验证试验的波浪参数
不同周期波浪作用下物模和数模系泊船舶运动量对比见图3。可以看出,物理模型试验和数值模拟的运动量模拟值是一致的,系泊船运动量的物理模型试验结果和数值模拟结果随周期变化的趋势基本一致。只有纵摇量值二者有一定的差别,但是纵摇运动量的值本身比较小,其绝对差别并不大。因此可以说明所建立的数值模型可以良好地反映出系泊船舶的运动情况,可以利用该模型进行不同周期和入射方向波浪作用时的系泊船运动的计算。
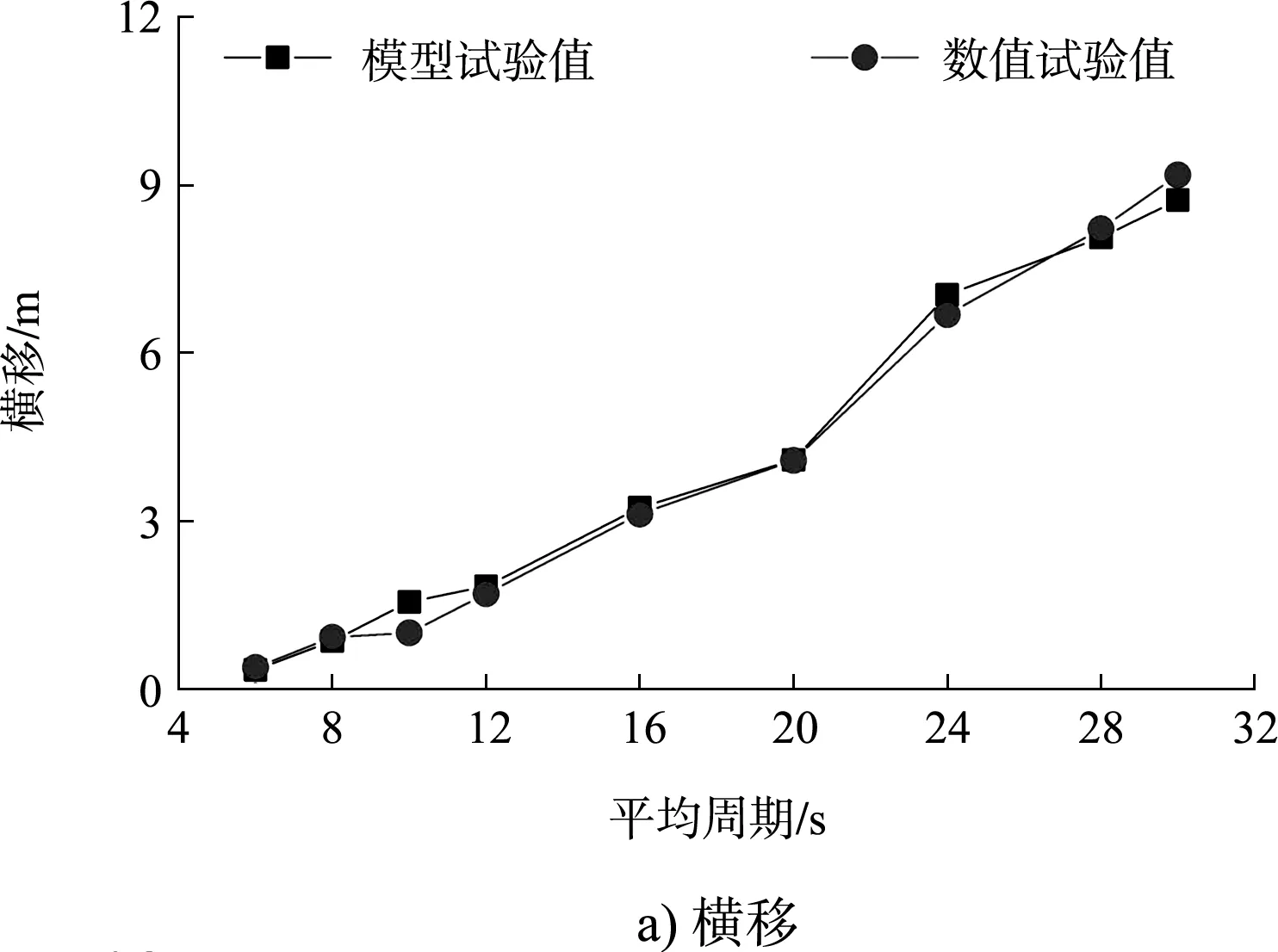
图3 不同周期波浪作用下物理模型和数值模拟系泊船舶运动量对比
4 不同入射方向和周期波浪对系泊船运动影响数值模拟分析
研究波浪的周期与入射角度对30万t系泊油船6个方向运动量的影响。数值模拟试验的具体波浪参数见表2,其中Tp为波浪的谱峰周期,频谱仍采用JONSWAP谱;θ为波浪的入射角,具体参见图1。需要指出,定义波浪入射角度与船舶纵轴线方向平行时为0°(顺浪),垂直时为90°(横浪)。为了更好地反映系泊船运动量规律,本文取各运动量峰值的1/3大值进行分析。

表2 试验的波浪参数
不同周期和入射角度波浪作用下系泊船横移运动量的变化曲线见图4。由图4a)可看出,不同周期波浪作用下的系泊船横移运动量随着波浪入射角度的增大而增大,横浪作用下的横移运动量最大,在顺浪作用下横移运动量基本为0 m。由图4b)可看出,横移运动量随着波浪谱峰周期的增大而增大,在波浪周期大于18 s时,60°、75°和90°这3个波浪入射方向的横移运动量相差不大;0°、15°和30°这3个波浪入射方向的横移运动量随周期增大时差别明显。
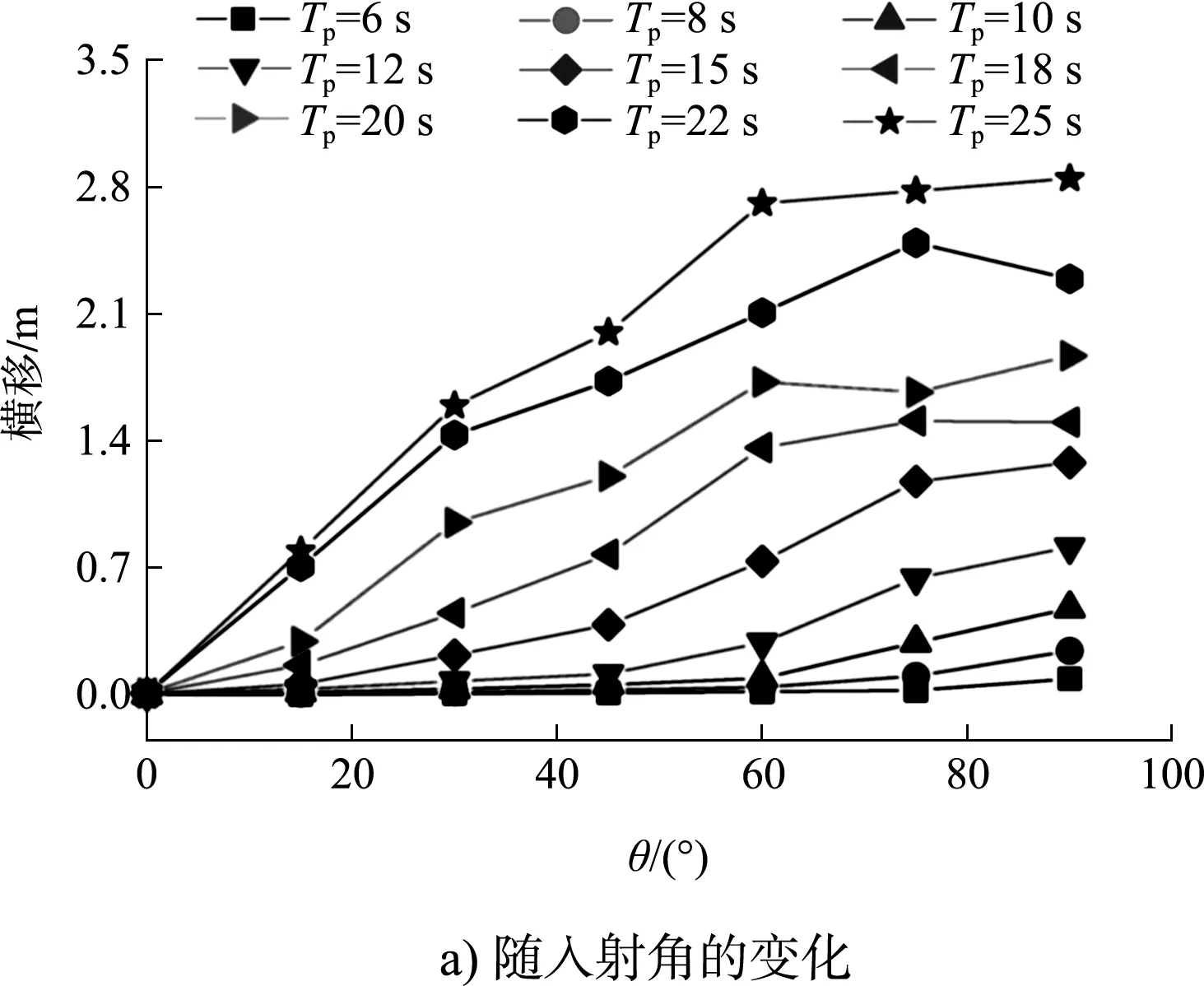
图4 不同周期与入射角度波浪作用下系泊船横移运动量的变化
不同周期与入射角度波浪作用下系泊船纵移运动量的变化曲线见图5。由图5a)可看出,在不同周期波浪作用下纵移运动量大体上随着波浪入射角的增大而先增大后减小,各周期下纵移运动量在波浪入射角度60°或75°时出现峰值,这是因为波浪的入射角度接近横浪时,纵移运动的响应相对减弱,且波浪入射角度接近顺浪时,波浪与船舶的作用面积相对减小,从而导致船舶整体的运动响应减弱。由图5b)可看出,纵移运动量基本上随波浪谱峰周期的增大而增大,但波浪入射角度接近横浪方向时,在船舶横摇周期附近纵移运动量突然减小,表现出随周期增大先减小再增大的现象,这是因为系泊船舶6个方向运动量相互影响,发生横摇共振时,船舶横摇运动增强,占主导作用,其他水平方向运动量略有减小。

图5 不同周期与入射角度波浪作用下系泊船纵移运动量变化曲线
不同周期与入射角度波浪作用下系泊船升沉运动量的变化曲线见图6。可以看出,船舶的升沉运动量随着波浪周期和入射角度的增大而增大。波浪周期较小时,升沉运动量随波浪入射角增大时变化的量值较小;波浪周期较大时,升沉运动量在不同入射角度波浪作用下的区分更为明显,当波浪入射方向靠近横浪或顺浪方向附近时,升沉运动量的值基本不变。

图6 不同周期与入射角度波浪作用下系泊船升沉运动量变化曲线
不同周期与入射角度波浪作用下系泊船横摇运动量的变化曲线见图7。由图7a)可知,横摇运动量基本随着波浪入射角的增大而增大,入射方向越接近横浪增大幅度越大。由图7b)可看出,波浪入射角度接近横浪时横摇运动量随着周期的增大先增大而后减小,当波浪的谱峰周期和船舶的横摇固有周期(T0=17.87 s)接近时,在波浪的作用下横摇运动发生共振,且在横浪方向达到峰值。而在波浪入射角度由横浪变化到顺浪时,共振的效果不断减弱。出现这种情况的原因是波浪为横浪时,波浪直接对横摇运动产生影响,当波浪入射角度偏离横浪时,对横摇运动产生影响的波浪分量就会减少。

图7 不同周期与入射角度波浪作用下系泊船横摇运动量变化曲线
不同周期与入射角度波浪作用下系泊船纵摇运动量的变化曲线见图8。可以看出,纵移运动量的量值相对较小。纵摇运动量随波浪入射角的增大表现出先增大后减小的规律,且由图8a)可知,随着周期的增大,纵摇运动量在不同入射角度波浪作用下的最大值将从横浪方向变化到顺浪方向。在图8b)中,波浪的入射角度θ≤45°时,系泊船舶的纵摇运动量随波浪周期的增大而增大;波浪的入射角度θ>45°,且波浪谱峰周期Tp≥18 s时,系泊船的纵摇运动量基本不发生变化。

图8 不同周期与入射角度波浪作用下系泊船纵摇运动量变化曲线
不同周期与入射角度波浪作用下系泊船回转运动量的变化曲线见图9。由图9a)可看出,当波浪周期Tp<18 s时,回转运动量随着波浪入射角的增大而增大。当Tp≥18 s时,回转运动量基本随着波浪入射角的增大先增大后减小,最大值出现在波浪入射角度为60°时。这是因为当波浪入射方向与船艏方向存在夹角时,使船舶横向和纵向的受力不均,船舶更容易发生偏转。在图9b)中,在大部分情况下,回转运动量基本随波浪周期的增大而增大,但在横浪作用下的回转运动量与纵移运动量类似,在波浪周期接近横摇周期处减小。
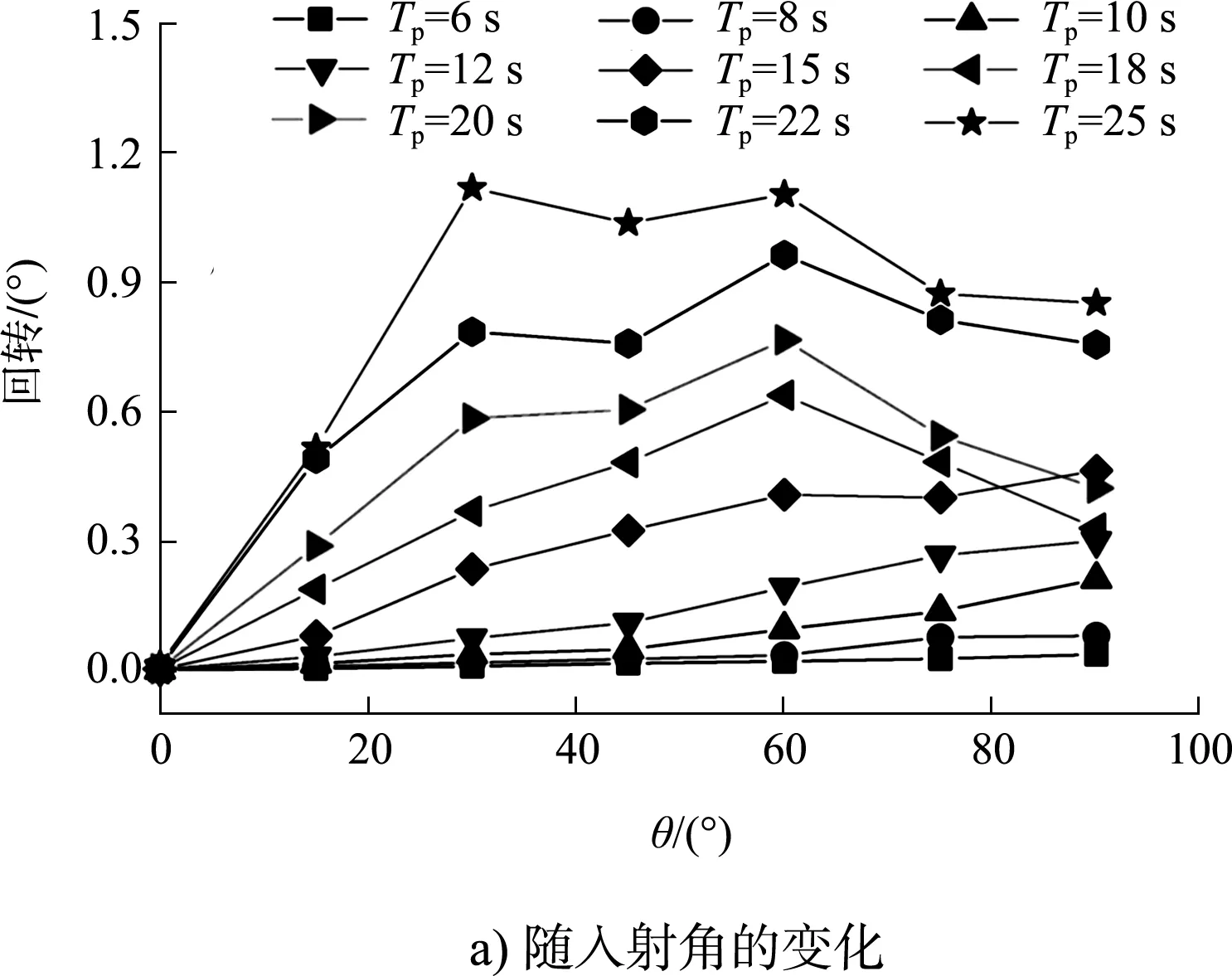
图9 不同周期与入射角度波浪作用下系泊船回转运动量变化曲线
5 结论
1)系泊船舶运动量随波浪入射角度和波浪谱峰周期变化的规律是相互影响的,在系泊船的纵移、回转和纵摇运动中较为明显。
2)不同波浪周期作用下,系泊船横移、横摇和升沉运动量随着波浪入射角度的增大而增大。当波浪谱峰周期和船舶横摇周期接近时会出现共振现象,横浪作用时横摇运动量会有大幅增加,而随着波浪入射角度偏离横浪方向,共振效果减弱。升沉运动量在波浪入射方向靠近横浪或顺浪方向附近时的值基本不变。
3)当波浪周期较长时,纵移和回转运动量均随着波浪入射角度的增大表现出先增大后减小的变化规律,且一般在波浪入射角度60°时出现峰值;在波浪周期较短时,回转运动量随着波浪入射角度的增大而增大。
4)在不同入射角度波浪的作用下,纵摇运动量的峰值随周期的增大,由横浪方向变化到顺浪方向。
