非饱和黏性地基土的土-水特征曲线试验及模拟*

魏占玺，谢东武，袁材栋，马文礼，李 元，李 云

(1.青海省环境地质勘查局，青海 西宁810007；2.青海九零六工程勘察设计院有限责任公司，青海 西宁810007；3.青海省环境地质重点实验室，青海 西宁810007；4.青海省地质环境保护与灾害防治工程技术研究中心，青海 西宁810007；5.同济大学 土木工程学院地下建筑与工程系，上海 200092)

港口基坑施工建设中，由于地下径流和降雨入渗的影响，地基土多为非饱和土，即固、液、气三相体系土。相比饱和土，非饱和土还有气相存在，土体内含有基质吸力，其力学性质更为复杂，影响港口地基的稳定性[1-2]。土-水特性是非饱和土力学中的核心内容，研究土-水特性对于掌握非饱和土工程特性、制定科学合理的设计方案具有较强的参考价值[3-4]。

关于非饱和土的土-水特性研究已有较多成果：Gardner[5]、Genuchten[6]和Fredlund[7]等最早提出几种不同的土-水特征曲线(SWCC)模型，至今在非饱和土-水特性研究中仍广为应用；王铁行等[8]、Ng等[9]、刘小文等[10]、刘永强等[11]和Jeong等[12]研究不同因素(如初始含水率、初始干密度、颗粒级配、温度、围压等)对非饱和土SWCC的影响，讨论不同因素对进气值、滞回特性等的影响规律；刘艳等[13]、Malaya等[14]、郭鸿等[15]和叶云雪等[16]系统研究了非饱和土SWCC的模拟预测。

本文研究背景为安徽淮北港基坑，以基坑内非饱和黏性地基土为研究对象，开展不同初始含水率、初始干密度、竖向应力以及干湿循环次数下的土-水特征曲线(SWCC)试验，探索非饱和黏性地基土在不同工况下的土-水特性。在前人已建模型的基础上，结合淮北港非饱和黏性地基土的土-水特性，得到修正模型，模拟不同工况下的SWCC，通过评分的方式得到适用于淮北港非饱和黏性地基土的推荐模型。研究成果可为不同工况下非饱和黏性地基土的土-水特性及港口地基稳定性研究提供参考。

1 土-水特征曲线试验

1.1 试验土样

试验土体基本物理参数见表1。所取土体黏土矿物主要为蒙脱石、伊利石，土样粒径大于2 mm、介于0.5～2 mm、0.25～0.5 mm、0.075～0.25 mm及小于0.075 mm的颗粒质量占比分别为9.24%、13.76%、12.38%、30.73%和33.89%。图1为采用击实试验得到的地基土击实曲线。

表1 土样基本物理参数

图1 地基土击实曲线

由图1可知，原状地基土最大干密度为1.61 g/m3，最优含水率为18.1%。由表1可知，塑性指数为18.8(>17)，定义为黏土[17]，本文地基土为非饱和黏性地基土。

1.2 SWCC试验方案

为开展不同初始含水率、初始干密度、竖向应力以及干湿循环次数下的土-水特征曲线(SWCC)试验，制备不同工况下的重塑土样，试验工况设置见表2。将原状土风干后过2 mm筛，按工况采用环刀法制备重塑样，SWCC试验前进行真空饱和。其中压实度=干密度/最大干密度，表2中的干密度设置参考现有水运、公路规范中地基土压实度90%、93%和96%的要求。

表2 试验工况设置

由表2可知，不同初始条件可组合为不同工况，其中C1、C2和C3反映不同初始干密度对 SWCC的影响，C2、C4和C5为不同初始含水率工况，C2、C6和C7为不同竖向压力工况，C2、C8和C9为不同干湿循环作用工况。

土-水特征曲线(SWCC)有多种试验方法，目前有体积压力板测试法、盐溶液法、Tempe仪测试法、滤纸法、Dew-point电位计法、TDR基质吸力量测法、GDS四维应力路径法等。体积压力板测试法便于操作，可量测基质吸力范围大，应用较广，但通常的体积压力板设备未考虑体积变化和竖向应力的影响。本文采用SDSWCC应力相关土水特征曲线压力板仪系统(图2)，区别于传统仪器之处在于可考虑体积变化和竖向应力的影响，由此开展不同干密度、初始含水率、竖向应力以及干湿循环次数下的SWCC试验。试验得到完整的SWCC曲线包含脱湿、吸湿曲线(图3)。

图2 试验仪器

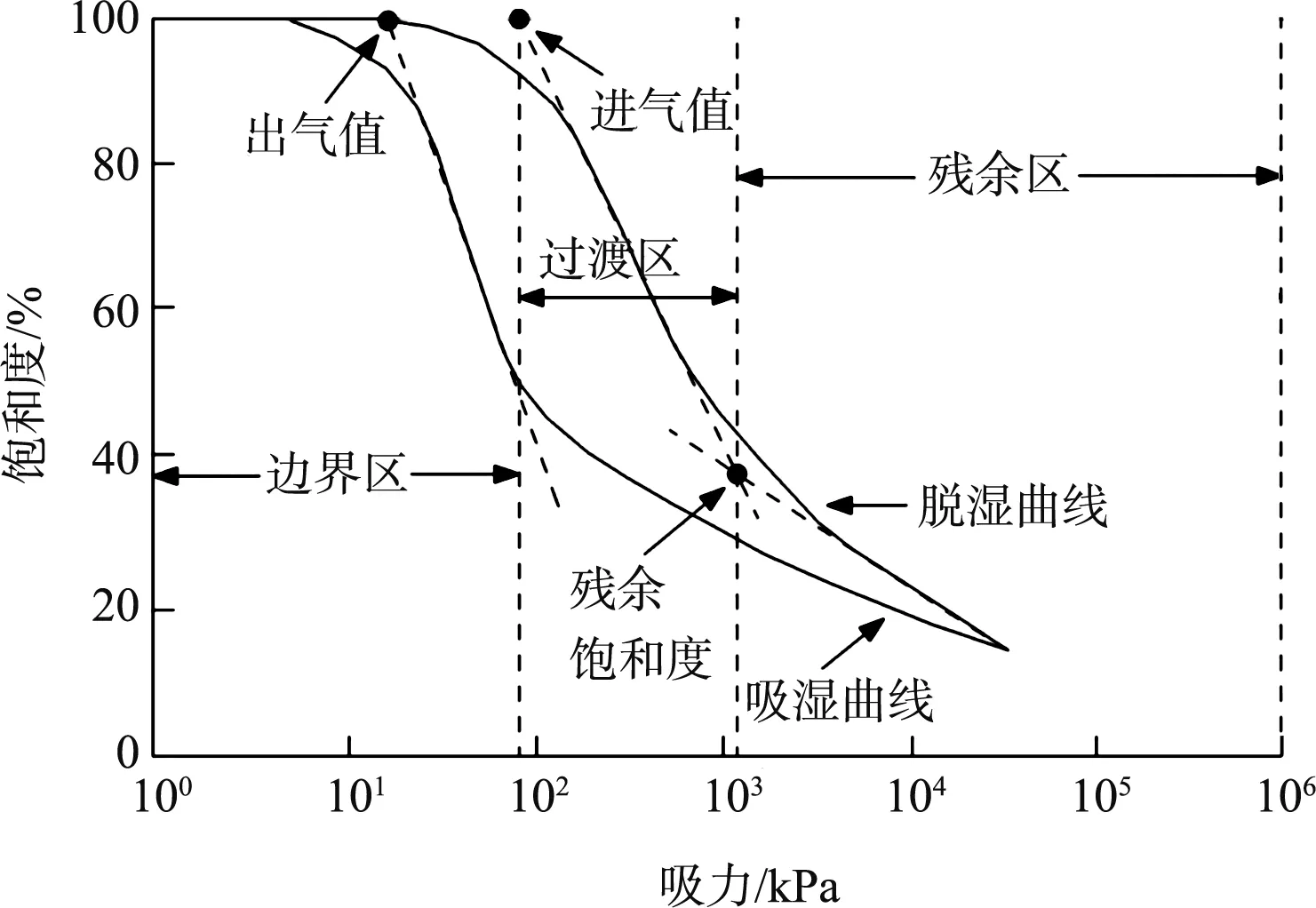
图3 土-水特征曲线

图3中脱湿曲线体现基质吸力增大引起的土体水分损失情况，吸湿曲线体现基质吸力减小引起的土体吸水情况。通过脱湿、吸湿曲线取双切线交点的方法将进气值、出气值和残余饱和度量化，为SWCC研究提供重要参数。

2 试验分析

2.1 不同初始含水率下的SWCC

初始干密度为1.50 g/m3的不同初始含水率下的SWCC如图4所示。由图4可看出，不同初始含水率下的SWCC脱湿、吸湿曲线形态、走势较为相似，说明初始含水率对土体脱湿、吸湿速率影响较小。通过图3所示取双切线交点的方法粗略判断，3种初始含水率下的进气值略大于出气值，随着初始含水率的提升，进气值、吸气值、残余饱和度递增。

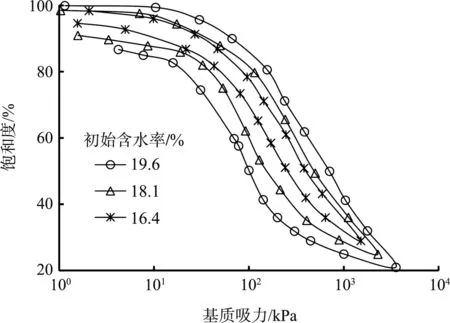
图4 不同初始含水率下的SWCC

SWCC具有明显的滞回特性，经过一个吸力循环变化后，土体饱和度的变化不可恢复。初始含水率为19.6%的滞回环面积最大，初始含水率为18.1%的滞回环次之，初始含水率为16.1%的滞回环最小且居中。其原因可能为：较低初始含水率下的土样孔隙大小不一，在空间上呈二元分布，进气值较小，土样不容易脱水。较高初始含水率下的土体孔隙主要为分布相对均匀的小孔隙，进气值更高，更容易脱水。非饱和土内部孔隙大小分布越均匀，瓶颈效应越明显，SWCC滞回环面积越大。瓶颈效应如图5所示。

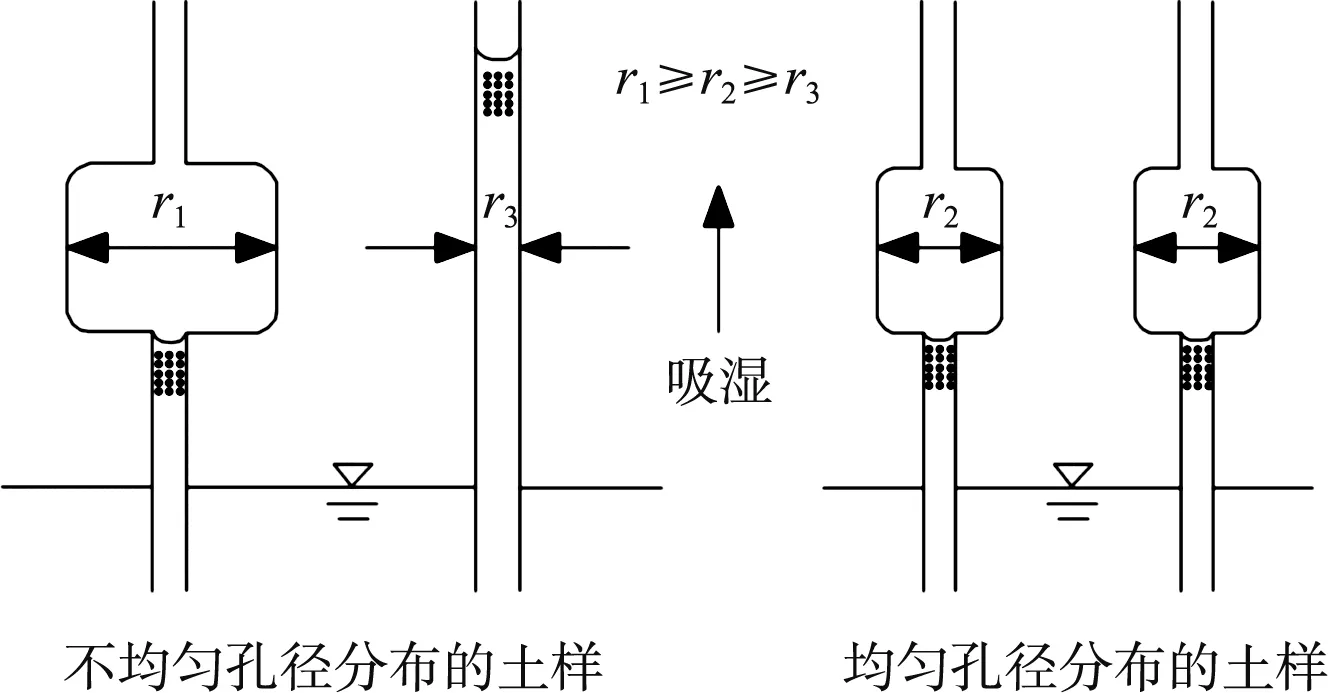
图5 瓶颈效应

2.2 不同初始干密度下的SWCC

初始含水率为18.1%的不同初始干密度下的SWCC如图6所示。由图6可看出，初始干密度对SWCC的过渡区和残余区影响显著，脱湿、吸湿曲线形态较为相似，脱湿曲线过渡区的斜率略大于吸湿曲线。通过图3所示取双切线交点的方法粗略判断初始干密度1.55、1.50和1.45 g/m3下的土体进气值分别为86、65和42 kPa，出气值分别为71、38和26 kPa，残余饱和度分别为41%、37%和23%，非饱和土进气值、出气值和残余饱和度皆随着初始干密度的增加而递增。由此认为，较高初始干密度非饱和土SWCC的进气值更大，脱水速率更慢，持水能力较强。其原因可能为：较高初始干密度非饱和土孔隙相对较少，孔隙之间的连通性差，因而进气值更大；较低初始干密度非饱和土孔隙相对较多，孔隙之间的连通性较好，在低基质吸力条件下也能较快地失水，因而进气值更小。

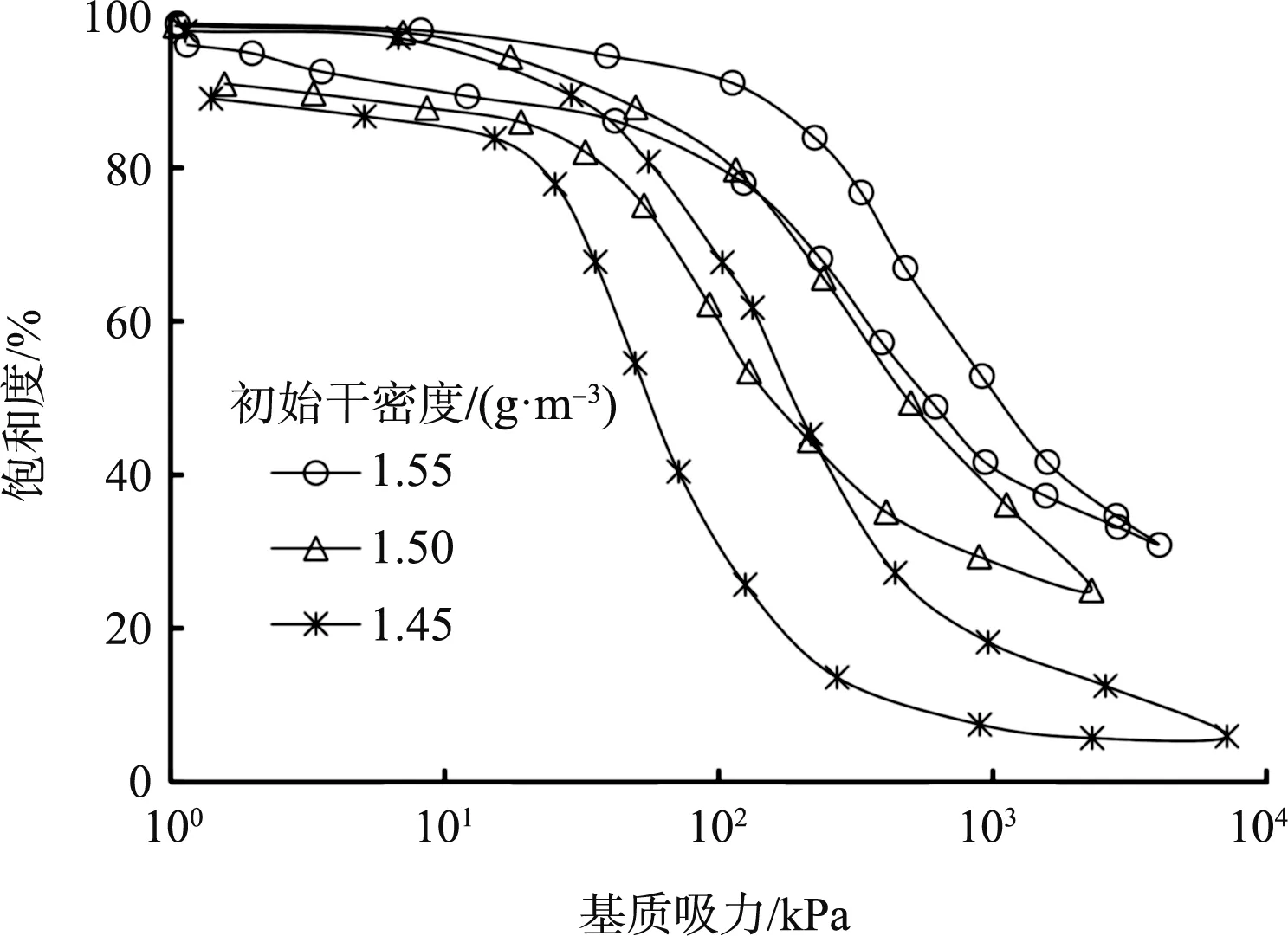
图6 不同初始干密度下的SWCC

图6中吸湿曲线均未达到完全饱和状态，初始干密度越大的试样，其残余饱和度越大，残余气体含量所占的比例越小。其原因可能为：非饱和土的初始干密度越小，其孔隙相对较多，毛细作用力更难排出孔隙内气体，土体更难恢复到完全饱和状态。

SWCC产生了大小不等的滞回环，SWCC产生滞回环的原因不仅在于瓶颈效应的影响，还与脱湿、吸湿过程中固、液接触角的差异相关。以斜面上水滴流动为例进行固、液接触角示意[18]，如图7所示。

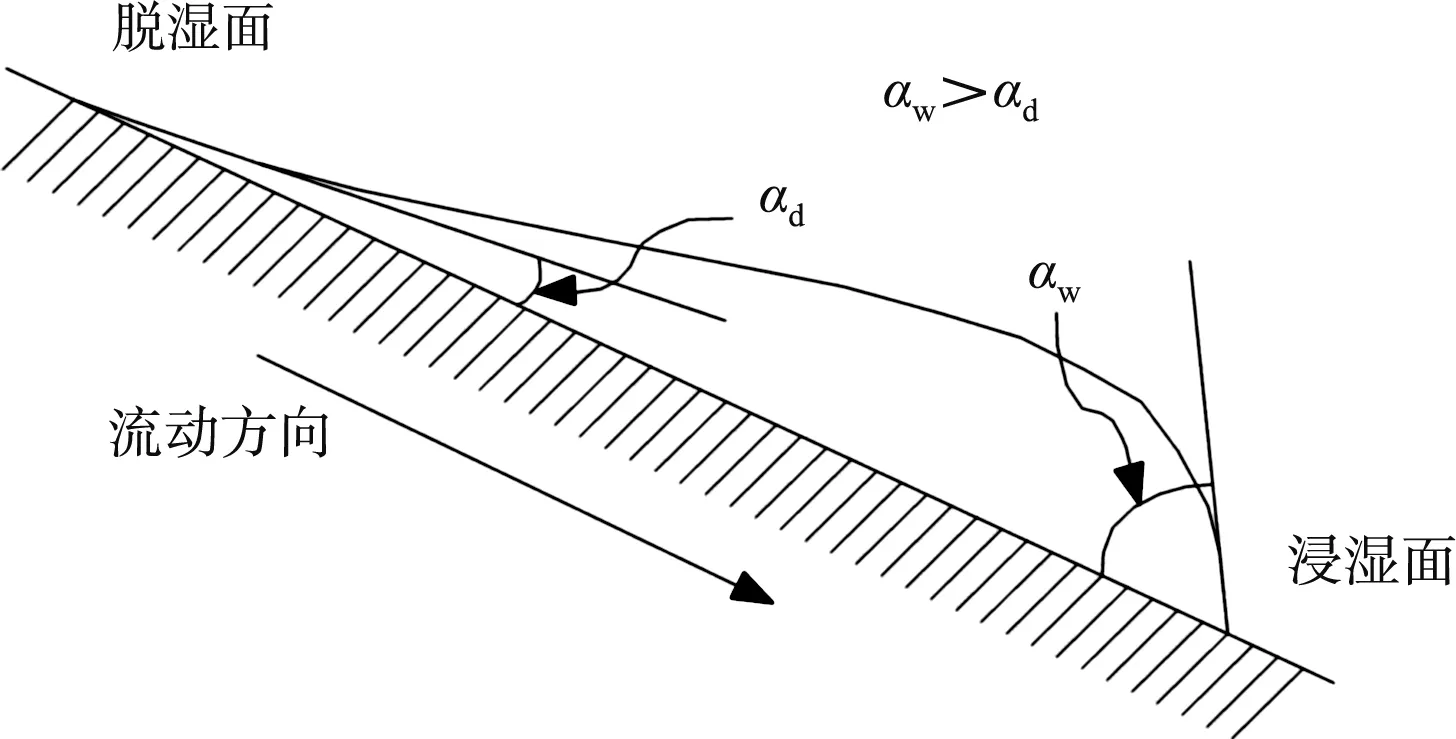
图7 斜面上水滴流动模拟固、液接触角

图7中以水滴向下流动的前进面作为脱湿面、后退面作为浸湿面，一般情况下浸湿面的固、液接触角αw大于脱湿面的固、液接触角αd。从图6可看出，滞回环大小随着初始干密度的减小而递增。非饱和土的初始干密度越小，土体内部结构越松散，孔径分布越不均匀，瓶颈效应越显著，由此非饱和土SWCC的滞回效应越明显。同时，较低初始干密度的土样孔径分布相对不均匀，大孔径的孔隙含量更多，大孔径孔隙在脱湿、吸湿过程中的固、液接触角变化更大，即(αw-αd)更大，导致滞回效应更显著。

2.3 干湿循环作用下的SWCC

初始干密度为1.50 g/m3、初始含水率为18.1%的不同干湿循环次数下的SWCC如图8所示。由图8可看出，不同干湿循环次数下的脱湿、速率相差不大。经历1次干湿循环作用的SWCC滞回环面积较大，经历3次和5次干湿循环的滞回环面积均较小且大小接近，说明干湿循环作用对SWCC有明显的影响，降低进气值和出气值；经历3次和5次干湿循环的进气值和出气值差异不大，说明干湿循环作用第1次附加在土体上时对SWCC影响显著，但随着干湿循环次数的增加，影响逐渐削弱。其原因可能为：土体脱湿过程中，土体骨架收缩，胶结物溶蚀，部分小孔隙连接贯通成大孔隙，增强了滞回效应；土体吸湿过程中，土颗粒间结合水膜进一步增厚，胶结物溶解，土体颗粒局部运移，最后土体结构趋于稳定。反复的干湿循环作用下，土体胶结物溶蚀、溶解程度衰减，土体内部结构不断调整逐渐趋于稳定，进气值、出气值的衰减程度变弱，滞回环面积减小，滞回效应减弱，干湿循环对SWCC的影响逐渐削弱。

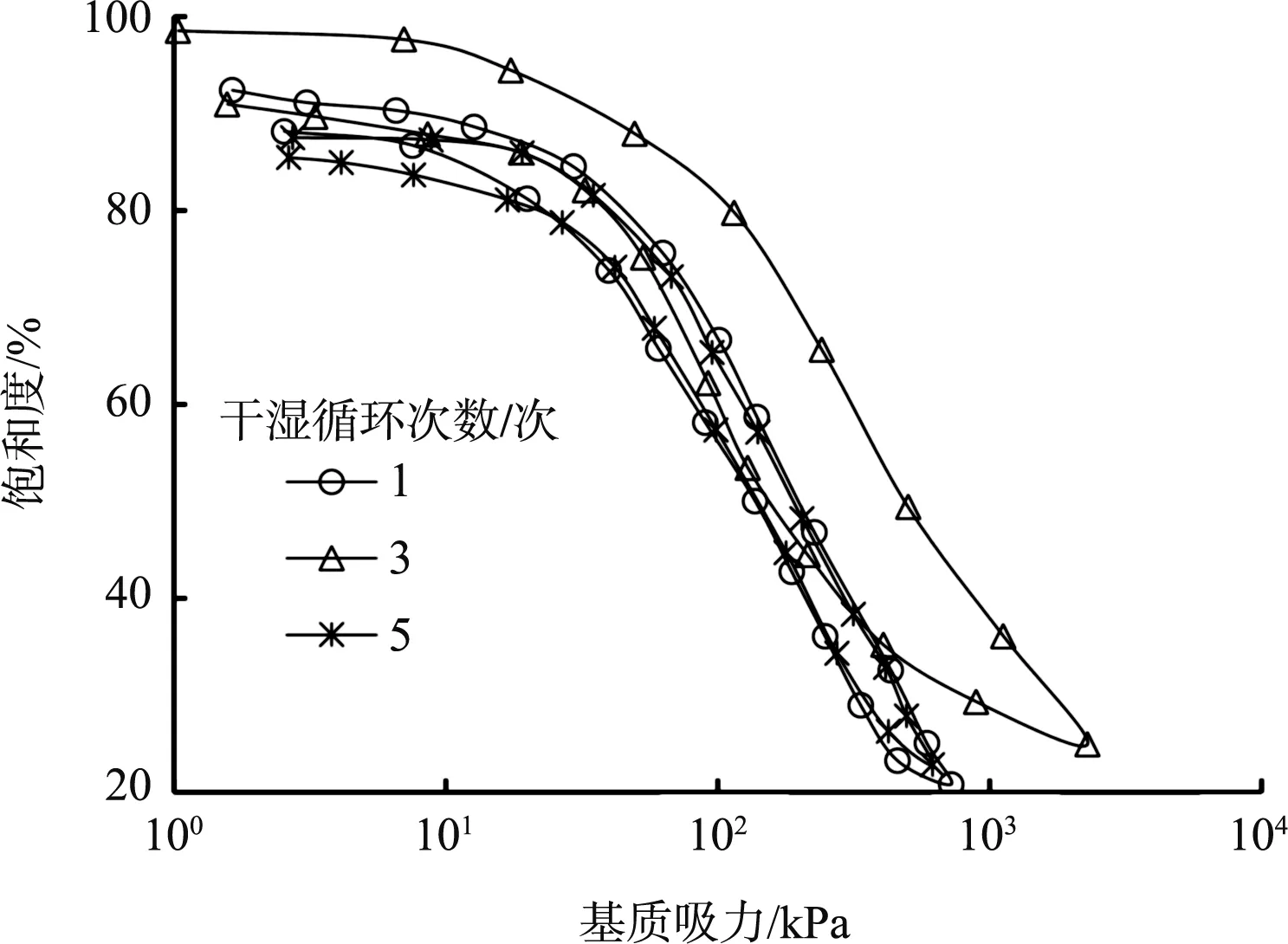
图8 不同干湿循环次数下的SWCC

2.4 不同竖向应力下的SWCC

初始干密度为1.50 g/m3、初始含水率为18.1%、干湿循环1次的不同竖向应力下的SWCC如图9所示。由图9可看出，竖向应力越大，进气值、出气值、残余饱和度越大，脱湿、吸湿速率越小。其原因可能为：竖向应力增大使得土体结构被压密，土体脱湿过程中孔隙比减小，吸入空气量更大，而吸湿过程中土体内有更多气体排出，由此进气值、出气值更大。图9和图6有相似之处，初始干密度和竖向应力均主要影响SWCC过渡区和残余区，说明竖向应力的作用对土体结构造成了密度变化，由此导致图9和图6变化规律相似。

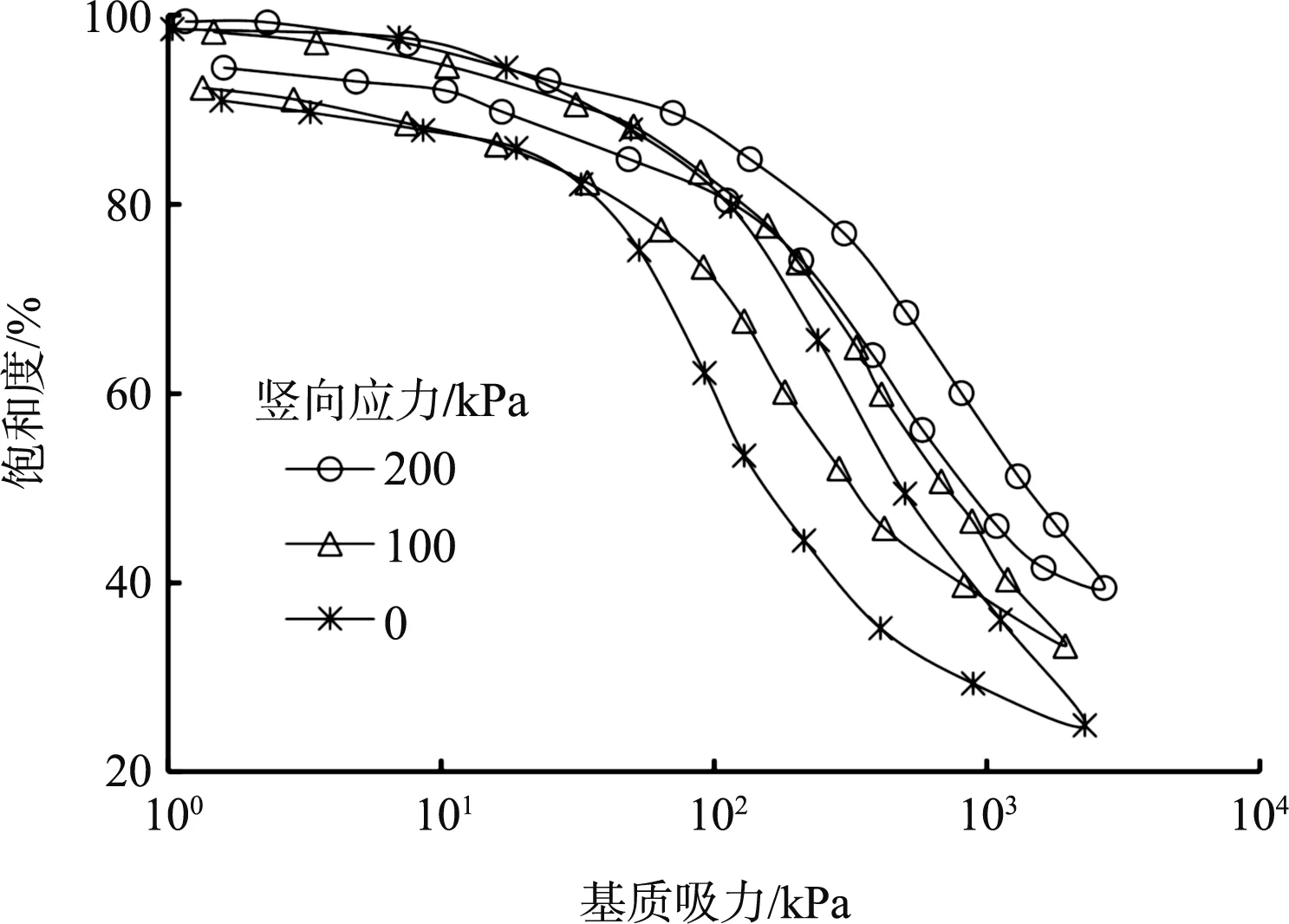
图9 不同竖向应力下的SWCC

3 土-水特性曲线模拟

3.1 土-水特性曲线模型

饱和度(体积含水量)在非饱和土瞬态分析中尤为重要，是SWCC模型中的重要参数，工程实践中可能限于现场条件等客观因素无法及时、准确获取，采取SWCC模型进行模拟求解无疑是一种可行的途径。目前已有较多SWCC模型，例如Gardner、Farrel、Van Genuchten、Mckee[19]、Fredlund &Xing、Likos[20]等模型，常用模型如下：

Gardner模型：

(1)

Van Genuchten模型：

(2)

Fredlund &Xing 1模型：

(3)

Fredlund &Xing 2模型：

(4)

式中：θ、θr和θs分别为土体体积含水量、残余含水量和饱和含水量，φ和φr分别为基质吸力和残余基质吸力，a、b和c皆为拟合参数。

实际上本文非饱和黏性地基土的SWCC曲线(图4、6、8、9)并不是典型的“S”型，残余含水量难以精确测定，因此在式(1)～(4)的基础上剔除残余含水量从而进行修正，得到如下修正模型。

Gardner修正模型：

(5)

Van Genuchten修正模型：

(6)

Fredlund &Xing1修正模型：

(7)

Fredlund &Xing2修正模型：

(8)

式中：S为模型拟合所得饱和度，d为拟合参数。

3.2 土-水特征曲线拟合

通过式(5)～(8)4个修正模型对本文C1～C9试样的土-水特征曲线进行模拟，拟合相关性系数R2通过下式计算：

(9)

式中：Si为试验实测饱和度。对不同修正模型的拟合结果评分，R2最高的记4分，以此类推，最低的记1分，拟合失败结果未收敛的记0分。

通过Origin软件，基于一般的非线性最小二乘法，分别采用式(5)～(8)拟合本文C1～C9试样的SWCC，各修正模型的拟合结果见表3。

表3 修正模型的R2及得分值

由表3可看出，模型拟合效果从好到差依次为Fredlund &Xing2、Fredlund &Xing1、Van Genuchten和Gardner修正模型，R2平均值分别为0.994 0、0.990 5、0.984 7和0.972 8，得分值分别为63、49、38和28。其中Van Genuchten和Gardner修正模型的R2小于0.99，拟合效果一般，Fredlund &Xing 2、Fredlund &Xing1修正模型的R2大于0.99，拟合效果较好，适用于本文非饱和地基土。尽管Fredlund &Xing1修正模型的R2略小于Fredlund &Xing2，但由于其模型结构简单，形式简练，工程实践中便于应用，综合考虑将其作为本文安徽淮北港基坑非饱和黏性地基土的推荐SWCC模型。

4 结论

1)初始含水率对非饱和土SWCC脱湿、吸湿速率影响较小，随着初始含水率的提升，瓶颈效应越明显，滞回环面积越大，进气值、吸气值、残余饱和度递增。

2)初始干密度对SWCC的过渡区和残余区影响显著，脱湿速率略大于吸湿速率。进气值、出气值和残余饱和度皆随着初始干密度的增加而递增。

3)SWCC进气值、出气值随着干湿循环作用的增强而递减，经历1次干湿循环作用的SWCC滞回环面积较大，但随着干湿循环次数的增加，SWCC滞回效应逐渐削弱。

4)非饱和土承受竖向应力越大，进气值、出气值、残余饱和度越大，脱湿、吸湿速率越小，竖向应力主要影响SWCC过渡区和残余区，与初始干密度对SWCC的影响类似。

5)本文非饱和黏性地基土SWCC并不是典型的“S”型，残余含水量难以精确测定。将残余含水量剔除后得到4种修正模型，分别拟合计算得到相关性系数和评分。对比发现，Fredlund &Xing1修正模型的拟合相关性系数较高，且模型结构简单，便于应用，适用于安徽淮北港基坑非饱和黏性地基土。