基于改进EWT的超高层建筑模态参数识别
2022-02-15郅伦海詹娟娟李阿龙
郅伦海, 詹娟娟, 李阿龙
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
超高层建筑结构的模态参数识别是国内外结构健康监测领域的热点研究课题之一,其核心思想是:基于结构振动响应信号,准确识别结构的模态参数(固有频率、阻尼比等),进而评估结构安全性、稳定性[1]。在台风、地震等自然环境激励下,超高层建筑结构的振动响应信号具有非线性、非平稳、动态响应小且噪声水平高的特性,基于这种数据难以准确地识别结构的固有频率和阻尼比[2]。
国内外研究者提出了各种基于自然环境激励下的结构模态参数识别方法,如小波变换(wavelet transform,WT)[3]和希尔伯特-黄变换(Hilbert-Huang transform,HHT)[4]等。WT理论基础完善,在建筑结构模态参数识别领域应用广泛,但其仅适用于平稳信号,对于小波基函数及其参数的选择复杂,且易受噪声信号影响。HHT主要分为经验模式分解(empirical mode decomposition,EMD)和希尔伯特变换(Hilbert transform,HT)2个部分,其核心是EMD。EMD能够自适应地分解非线性、非平稳信号,但缺乏完备的理论基础,在信号分解时易出现端点效应明显、模态混叠、虚假模态、分解不正交等问题。针对这些问题,文献[5]提出经验小波变换(empirical wavelet transform,EWT),该方法综合了WT和EMD的优点,能够自适应地分析噪声信号的傅里叶频谱,自适应地进行分割,以此构建小波滤波器组,将多分量原始信号分解为若干调频调幅分量。然而,在信噪比较低的情况下,傅里叶频谱极易出现频率泄露、对噪声敏感和虚假极值等问题,导致EWT中频谱的划分出现误差,无法准确地分离出有物理意义的各阶模态。
针对上述情况,文献[6]提出了一种改进的EWT,其核心在于用基于Burg算法的自回归(autoregressive,AR)模型功率谱[7]代替傅里叶频谱分割信号频带,以改善EWT中粗糙的频谱分割问题;采用该方法处理低信噪比和不稳定信号时,鲁棒性好、自适应性强、可更准确地估计信号频带边界,有效避免了过度分解和混叠现象,而且拟合结果十分优越,能快速精确地识别出结构的低阶频率和阻尼比。本文将该方法用于超高层建筑结构领域,再结合自然激励技术(natural excitation technique,NExT)[8-9]及归一化的希尔伯特变换(normalized Hilbert transform, NHT)[10-11],发展一种环境风激励下基于改进EWT的超高层建筑结构模态参数识别方法;通过对4层框架结构数值模型的模态参数识别验证了其正确性和有效性,通过将其应用于台风下台北101大楼的模态参数识别,研究了其适用性。
1 理论基础
1.1 EWT
EWT是一种能够有效分析噪声非稳态和非线性信号的自适应时频分析方法[5],可将原始信号f(t)分解为A+1个本征模函数fk(t)之和,即
(1)
分解过程主要有2步:① 对傅里叶谱进行自适应分割,以选择合适的正交小波滤波器组;② 滤波器组构建及信号重构。信号f(t)经过EWT分解得到的单分量调频调幅函数fi为:
(2)
(3)
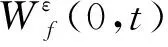
1.2 基于Burg算法的功率谱估计
为改进传统EWT对于低信噪比信号频带边界划分不准确的问题,根据文献[6],采用基于Burg算法的AR模型功率谱代替傅里叶谱划分频谱边界。功率谱密度(power spectral density,PSD)反映了单位频带内信号功率随频率的变化情况,信号功率谱的计算公式为:
(4)
其中:rx(m)为信号x(n)的自相关函数;N为信号x(n)的长度。采样数量为2M+1。
AR模型反映的是功率谱峰值,工程应用方便[12]。假定信号序列x(n)是由均值为0、方差为σ2的白噪声u(n)激励的线性系统输出,AR参数模型的差分方程为:
n=0,1,2,…
(5)
其中:ak为AR系数;p为预设的模型阶数。AR模型的标准方程式为:
(6)
x(n)的AR功率谱P(ej ω)公式为:
(7)
1.3 NExT
采用文献[8]提出的NExT,可以求出单分量信号的自由衰减响应。对于一个自由度为D的线性系统,k、i为该系统的2个测点,测点i为参考点。当系统在k点受到脉冲激励fk(t)时,i点产生的脉冲响应为:
(8)
其中:φir为测点i的第r阶模态振型;akr为常数项,其数值只与参考点i和模态阶数r有关;eλi(t-p)fk(p)包含了结构的响应信息,即模态频率和模态阻尼比。
当结构在k点受到单位脉冲激励时,i点的脉冲响应函数hik(t)为:
(9)
当结构在k点受近似白噪声的激励时,i、j点的互相关函数为:
(10)
其中,bjr为仅与参考点j的位置和模态阶数r、s有关的常数。
对比(9)式、(10)式可以发现,线性结构任意两点的响应互相关函数与脉冲响应函数都是一系列复指数函数的叠加,有同样的数学形式。因此,在时域进行模态参数识别的过程中,使用响应互相关函数代替脉冲响应函数是可行的。
1.4 NHT
为改进HT受Bedrosian定理约束的问题,文献[10]提出NHT。NHT首先对通过EMD分解得到的固有模态函数(intrinsic mode function,IMF)进行归一化处理,再对归一化后的IMF作HT,便可不再受Bedrosian定理的限制。处理流程[13-14]如下:
(1) 对响应信号进行EMD分解得到一系列IMF分量D(i),求每个D(i)的绝对值|D(i)|,寻找D(i)中的所有局部极大值,使用三次样条曲线对所有局部极大值点进行拟合,得到经验包络信号E1(i)。
(2) 用经验包络信号E1(i)对IMF分量进行归一化处理。y1(i)=D(i)/E1(i),若y1(i)≤1,结束归一化处理;否则,重复步骤(1),直至满足y1(i)≤1。由上述归一化过程,可将IMF分量D(i)表示为调幅与调频分量的乘积。
D(i)=Ae(i)yn(i)
(11)
其中,yn(i)为调频分量;Ae(i)为调幅分量,该分量为瞬时幅值,即
Ae(i)=E1(i)E2(i)…En(i)
(12)
(3) 对yn(i)作HT求得瞬时相位,即
θ(t)=arctan(y(t)/x(t))
(13)
通过对瞬时相位函数求导可得到瞬时频率,即
(14)
1.5 曲线拟合求出阻尼比
对单分量响应信号采用NExT技术后,得到自由衰减信号的包络线,利用曲线拟合方法把衰减曲线拟合到包络线上就可以估计出单模态信号的阻尼比,公式为:
f(t)=Aeb t,b=-2πωξ
(15)
其中:A为拟合包络的幅值;b为指数衰减函数的功率值。则阻尼比ξ为:
ξ=-b/(2πω)
(16)
1.6 模态参数的识别过程
对待处理的多分量信号,首先用基于Burg算法的AR功率谱分割信号频带,以此构建小波滤波器组,从而对响应作EWT得到一系列IMF,再使用NExT得到各个IMF的自由衰减响应,最后使用NHT得到瞬时幅值和瞬时频率,并通过曲线拟合的方式拟合该模态的阻尼比和自振频率。结构模态参数识别方法的流程如图1所示。
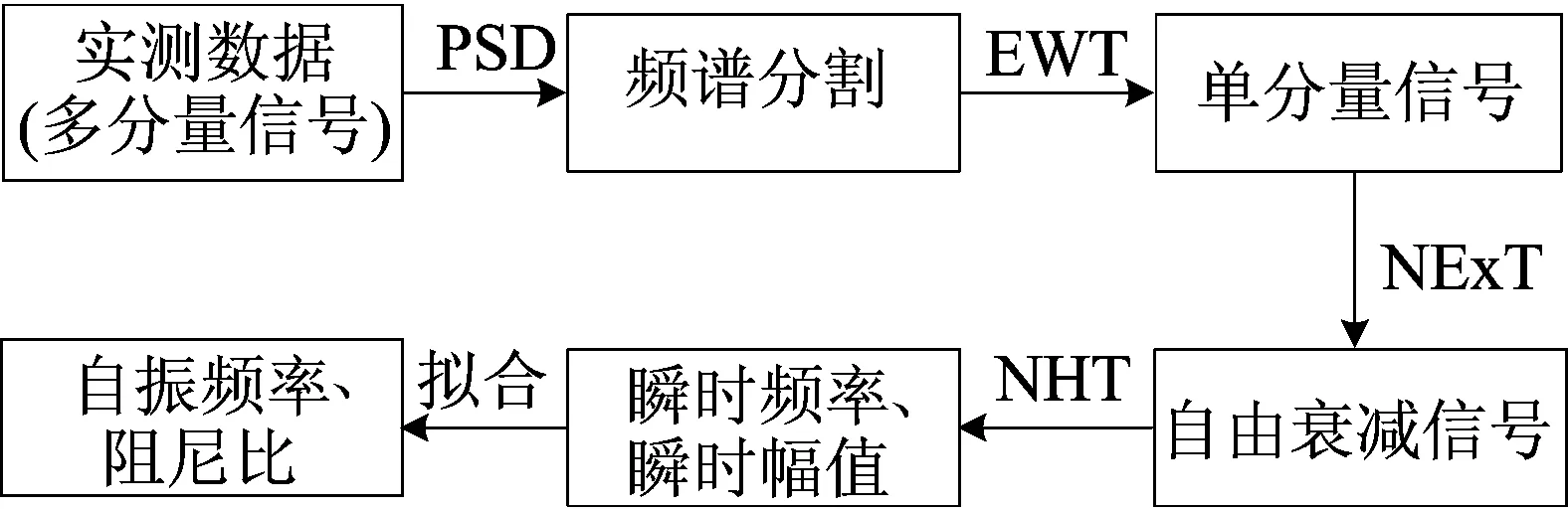
图1 结构模态参数识别方法流程
2 数值模拟验证
以一个4层钢筋混凝土框架结构模型的数值算例,验证上述模态参数识别方法的有效性和准确性,4层框架结构的模型如图2所示。该结构模型的相关物理参数如下:每层楼的质量为m1=m2=m3=m4=200 kg,每层楼刚度为k1=k2=k3=k4=1 000 kN/m,每层楼阻尼为c1=c2=c3=c4=1 kN·s/m。在结构顶层施加一个非平稳f(t)激励持续作用1 000 s,f(t)表达式为:
(17)
采用轮次检验法检验该激励的非平稳性,结合Newmark-β法求得该结构的加速度响应,如图3所示,其中采样频率为20 Hz,响应信号f(x)的傅里叶频谱如图4所示。
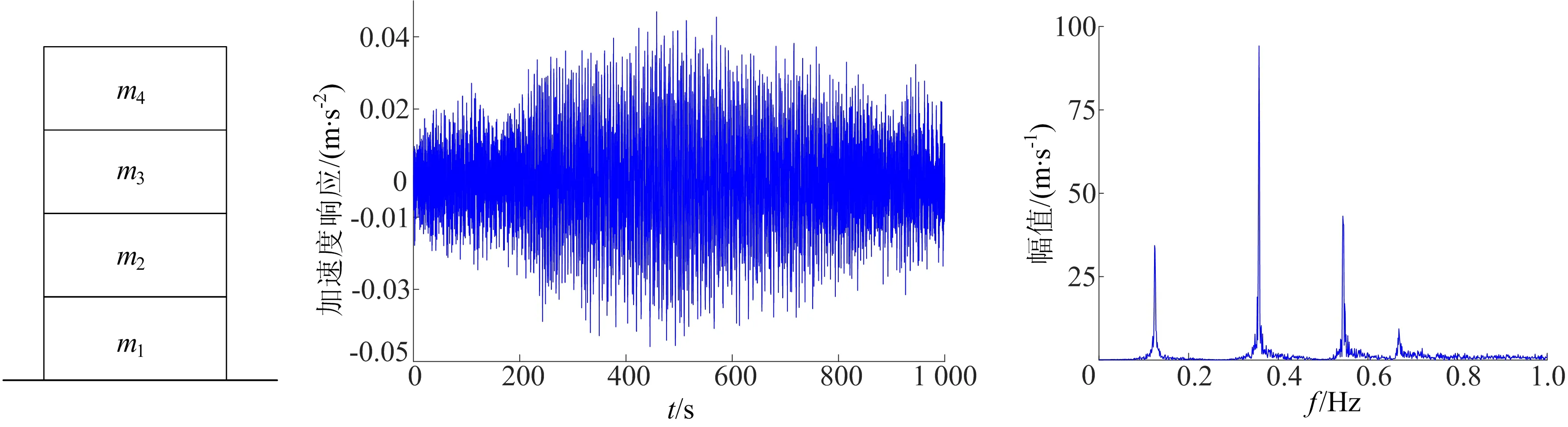
图2 4层框架结构模型 图3 数值算例加速度响应 图4 数值算例响应信号的傅里叶频谱
信号频带划分边界如图5所示。从图5a可以看出,用传统的EWT方法划分频带边界,仅第1阶信号可被明显划分,第2阶、第3阶的主峰和旁瓣被分割在不同的频带中,第4阶和第3阶信号混叠,没有被单独分割出来,无法准确地划分频谱区间。从图5b可以看出,使用改进EWT方法划分信号频带,结构的每阶模态都可被划分到不同的频带中,不存在过度分解和模态混叠现象,能更加准确地提取出结构的各阶模态响应。同时对比图5a和图5b可以看出,信号的AR功率谱比傅里叶谱曲线更加光滑,因此改进EWT方法的抗噪性更加优越。
基于图5b的频带划分,并结合EWT方法对上述框架结构加速度响应信号进行模态参数识别。框架结构的第1阶模态拟合结果如图6所示,第2阶至第4阶模态拟合结果如图7所示。
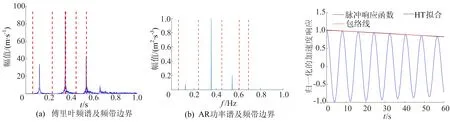
图5 数值算例信号频带划分边界 图6 数值算例第1阶模态拟合结果
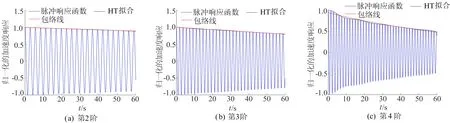
图7 数值算例第2阶至第4阶模态拟合结果
从图6、图7可以看出,包络线十分平滑,曲线拟合效果优越,可提高识别结果的可信度。模态参数识别结果与结构动力学分析计算得到的理论值对比见表1所列。由表1可知,识别结果与理论值基本一致;对于自振频率,识别结果精确度良好,每阶误差都在1%以内,尤其是第2阶频率计算值与理论值十分接近;对于阻尼比,最大误差不超过14%,各阶模态识别值的误差分别为7.14%、3.57%、4.11%、13.04%。以上结果表明,本文提出的模态参数识别方法具有较好的准确性和适用性。
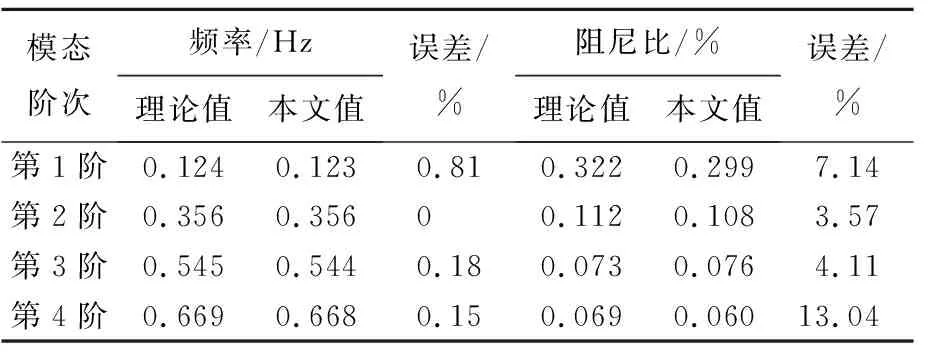
表1 模态参数识别结果与理论值对比
3 台北101大楼的模态参数识别
3.1 台北101大楼及相关数据
台北101大楼有一套健康监测系统,该监测系统包括强震仪和数据采集设备2个部分,数据采集设备的采样频率为200 Hz,可以监测主体结构的加速度响应。强震仪布置立面图如图8所示[2]。
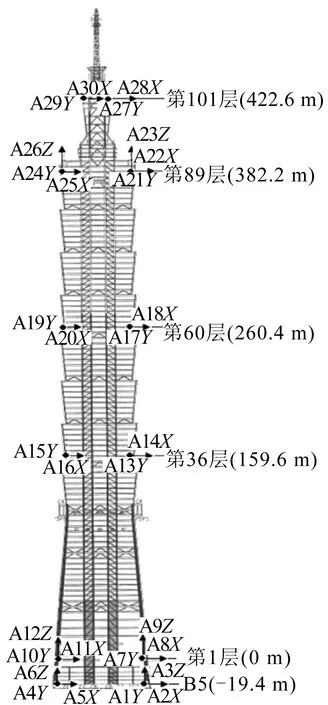
图8 台北101大楼健康监测系统强震仪布置立面图
台北101大楼位于中国台湾省台北市信义区,是台北的地标性建筑,其主塔楼为101 层的办公楼,地面以上总高度为508 m,其中包括448 m的结构总高度和60 m高的顶部尖塔。主塔楼结构的平面布置为正方形,各层边长不等,以45.9 m为主,结构高宽比接近于10,超过现行结构规范规定的标准,属于对风作用敏感的结构。
本文基于台北101大楼健康监测系统2005年对台风“海棠”影响下的风致响应监测结果,利用其顶部(第101层,422.6 m)处28X方向和27Y方向的加速度响应数据对本文模态参数识别方法的准确性和适用性进行验证。
3.2 模态参数的识别结果
台风“海棠”作用下台北101大楼X、Y方向的加速度响应时程及X方向频谱如图9所示,Y方向加速度响应频谱如图10所示。

图9 X、Y方向加速度响应时程及X方向频谱
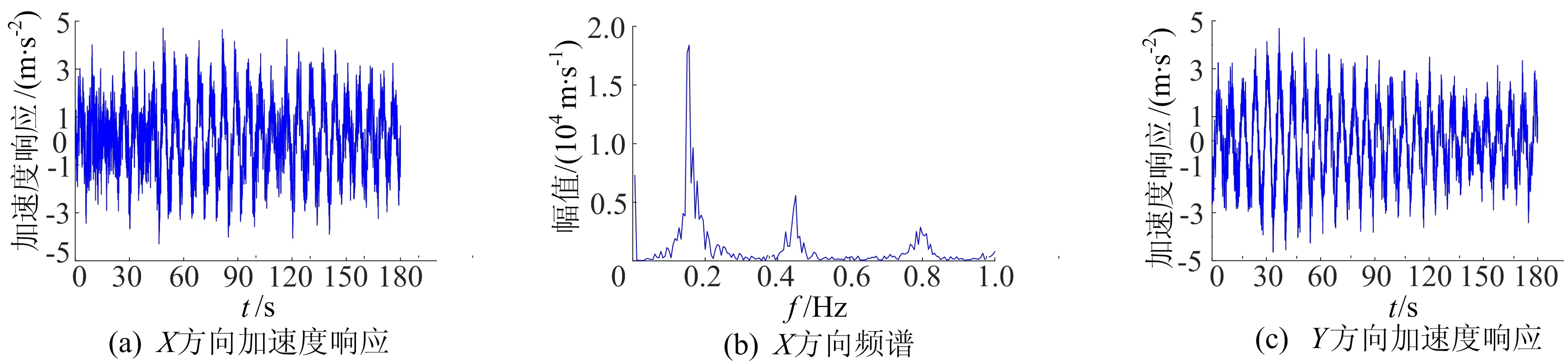
图10 Y方向加速度响应频谱 图11 傅里叶频谱及频带边界
X、Y方向加速度时程响应的傅里叶频谱及频带边界如图11所示,X和Y方向加速度时程响应的AR功率谱及频带边界如图12所示。从图11可以看出,传统EWT频带边界划分方法存在过度分割问题,其中X和Y方向的第1阶信号被多次分割,主峰和旁瓣被分割在几个不同频带。从图12可以看出,改进EWT中的边界划分方法避免了上述问题的产生,可以很好地划分出各阶信号频带,以便于后续准确地将信号分解为各个单分量信号,即每阶模态响应。限于篇幅,本文给出Y方向加速度响应采用EWT的分解结果及相应频谱图,如图13所示。从图13可以看出,传统EWT方法存在过度分解现象,其中第1阶模态被过度分解为中心频率相似的2个单分量信号。Y方向响应采用改进EWT的分解结果及相应频谱如图14所示。从图14可以看出,加速度响应被明显地分解为几个单分量信号,且各个单分量信号的中心频率、幅值与实际情况吻合。因此,改进EWT方法可更准确地估计信号频带边界,且自适应更强,能有效避免过度分解现象。
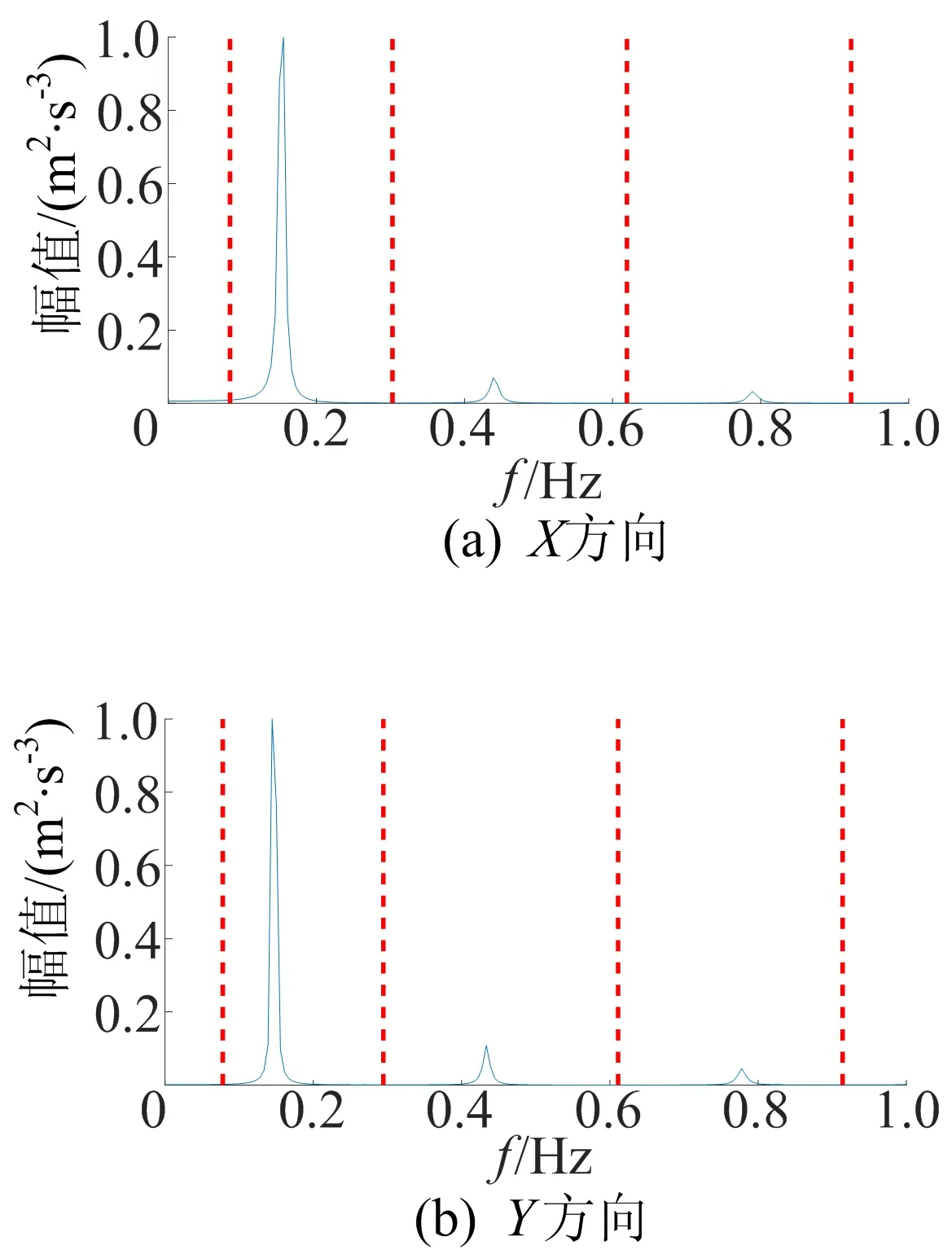
图12 AR功率谱及频带边界

图13 Y方向响应采用EWT的分解结果及相应频谱

图14 Y方向响应采用改进EWT的分解结果及相应频谱
对于改进EWT方法分解得到的单分量信号,通过NExT、NHT和曲线拟合得到自振频率和阻尼比。Y方向3阶模态拟合结果如图15所示。从图15可以看出,各阶包络线十分平滑,包络线符合指数自由衰减曲线。2种方法识别阻尼比和自振频率对比见表2所列。
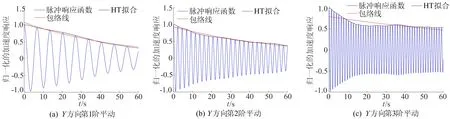
图15 Y方向各阶模态拟合结果
由表2可知:对于自振频率,2种方法识别出的X、Y方向前2阶频率十分接近;对于阻尼比,2种方法识别出的X、Y方向前2阶阻尼比都在合理范围,但传统EWT方法无法识别出第3阶频率和阻尼比。因此,本文基于改进EWT的模态参数识别方法可有效避免过度分解现象,能快速精确地识别出结构的高阶频率和阻尼比。
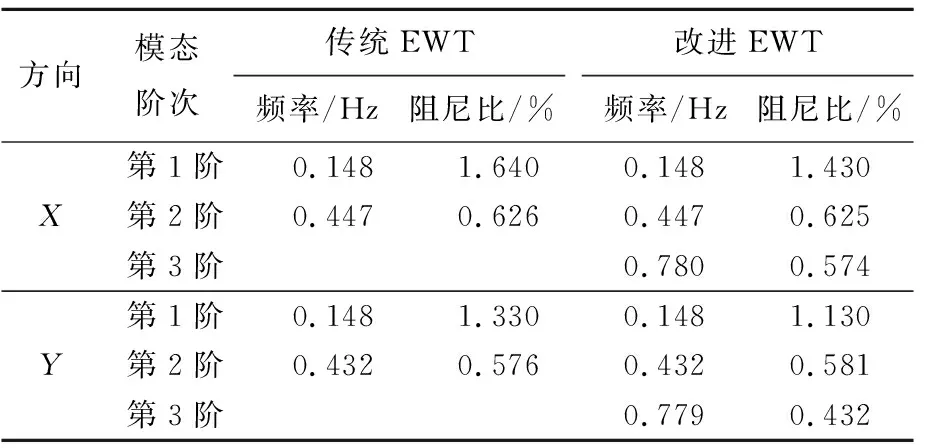
表2 2种方法识别阻尼比和自振频率对比
为一进步了解台北101大楼的模态振型,本文利用第6层测点的加速度响应数据,以地下第5层作为参考测点,通过NHT得到各个测点之间的振幅比及相位差特性,确定结构的平动振型[15],平动振型的大小由结构上任意2个测点瞬时幅值的比值α决定,其方向由相位差决定。分别用本文方法和有限元模型计算[16]得到结构X、Y方向振型如图16所示。从图16可以看出:通过本文方法获取的第1阶振型整体平动,第2阶振型上、下相对振动,第3阶振型表现为顶部和底部同向平动,结构中部反向平动。图16结果表明,本文方法识别的前2阶振型和有限元模型结果吻合较好。
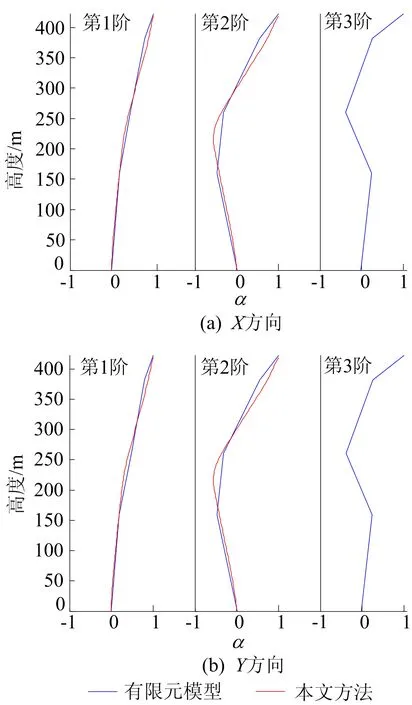
图16 X、Y方向振型本文方法和有限元模型计算结果对比
此外,本文通过模态置信准则(modal assurance criterion,MAC)来评估实测模态向量和理论模态向量的相关程度[17],其公式为:
(18)
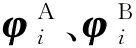
4 结 论
本文基于改进EWT、NExT及NHT发展一种超高层建筑结构模态参数识别方法,采用该方法对4层框架结构模型和台风“海棠” 激励下台北101大楼的模态参数进行识别,结果验证了该方法的正确性、有效性和适用性。主要结论如下:
(1) 在处理低信噪比和不稳定信号时,传统EWT方法中的傅里叶频谱分割效果欠佳;本文将改进EWT引入超高层建筑结构模态参数识别领域,该方法用基于Burg算法的AR功率谱替代傅里叶频谱划分频谱区间,可提高频率边界划分准确性,有效避免过度分解和频率混叠现象。
(2) 使用4层框架结构模型对本文模态参数识别方法进行验证,结果表明,该方法可准确识别结构的频率和阻尼比,与理论值接近,验证了该方法的准确性和有效性。
(3) 对2005年台风“海棠”影响下台北101大楼的结构响应进行模态参数识别分析,识别出的频率、阻尼比都在合理范围,模态振型与有限元识别结果吻合较好,验证了本文方法适用于自然环境激励下的非线性非平稳信号,抗噪性好。
