面向植被边坡的地基SAR高相干点选择
2022-02-14田卫明邓云开聂祥飞冯丽源
杨 鸿 田卫明 邓云开 聂祥飞 冯丽源 张 月
(1.重庆三峡学院电子与信息工程学院,重庆 404130;2.北京理工大学信息与电子学院,北京 100081;3.北京理工大学重庆创新中心,重庆 401120)
1 引言
滑坡是最常见、危害最大的地质灾害之一。以地表的形变数据为基础,结合其形变机理和力学机制,有利于实现对滑坡灾害的预测预警[1]。GB-SAR(Ground-based synthetic aperture radar,地基合成孔径雷达)具有全天候、非接触、高精度、近实时等测量优点,近年来在形变监测领域广泛应用[2]。
地基SAR 通常是基于差分干涉测量技术[3],通过对同一监测区域进行多次观测后获取的SAR 复图像进行处理,实现地表形变测量[4]。由于受到系统热噪声、大气扰动等误差源的影响,导致干涉相位图中部分像素点的相位质量很低,对地表形变的准确性构成很大干扰。因此需要选择出高相位质量的像素点(即高相干点)进行形变分析,以保证形变测量的准确性[5]。
在地基SAR 领域中,广泛使用幅度离差法进行高相干点的选择。通过计算每一个像元在多幅SAR 图像中的幅值标准差与幅度均值的比值,然后设置合理的门限进行PS 点的选择。该方法能有效应用于岩质边坡或者城镇场景。但对于植被边坡,由于场景中缺少裸露岩石等高相干目标,采用幅度离差法所选择出的PS数量很少,不利于形变分析。
在星载SAR 领域,为提高植被边坡高相干点数量,国外研究学者主要提出了两种解决方法。第一种是StaMPS[6]干涉方法,该方法核心是基于相位信息选择幅度低稳定、相位高稳定的像素点;第二种是SqueeSAR[7]技术,该方法核心是选择DS点,即[8-9]一定范围内像素点服从同一幅值分布,且相位整体稳定的散射体。以上两种解决方法已广泛应用于星载SAR领域,考虑到星载SAR与地基SAR工作原理的差异性,需要研究在地基SAR领域的适用性。
针对上述问题,本文在StaMPS 方法的基础上,首先采用幅度离差法获取PSC(Candidate Permanent Scatterers,候选永久散射体)集合,然后利用非PS点来计算相干系数门限,通过该门限实现高相干点的选择,最后引入DS 选择技术来进一步提高高相干点选择的数量。本文详细介绍了改进方法的实现过程,并对一处植被边坡监测场景的SAR 图像进行了处理与分析,通过与常规高相干点选择方法进行了对比分析,验证了本文方法的有效性和适用性。
2 实验信息
本实验选定重庆万州区九道拐形变监测区域,该区域为典型的植被山体边坡,图1 所示为场景照片,其中包含崖壁、山路、峡谷和乡村,其中在峡谷周围及乡村区域除了建筑物外,还有很多裸露的土壤,这些区域就是实验中需要识别出来的高相干点区域。该山体边坡地处长江北岸,位于万州区钟鼓楼街道、李家河沟北东侧,平面形态呈圈椅状,坡体纵向长约170 m、横向宽约300 m,平均厚度8 m,体积约25万方[10]。
实验中采用一部线扫描地基SAR[2,11]对该植被山体边坡进行了监测,系统的主体部分包括高分辨调频连续波(FMCW)雷达、高精度电控位移台组成,系统主体外观如图2所示。线扫描地基SAR工作在Ku波段,可以获取达到亚毫米量级的高精度形变信息。表1为地基SAR测量系统参数。

表1 雷达系统参数Tab.1 Radar system parameters
现在对2020 年5 月24 日0 时~3 时连续采 集的30 幅雷达图像进行分析,两幅SAR 复图像的平均获取时间约为6 分钟,最短时间基线为5 分钟。图3(a)所示为30 幅SAR 复图像的平均幅值图,图中对所有像素点的幅值进行了dB 归一化处理。选择时间基线最短的两幅SAR 复图像生成1 幅干涉相位图,如图3(b)所示。从直观上可以看到图中存在很大数量的像素点的相位质量较低,这对地表形变的准确性产生很大干扰,因此选择高相位质量的像素点是保证地表形变分析准确性的关键。
在利用地基SAR 进行形变测量时,一个像素点的相位信息由于时空去相关的影响而存在较大误差,导致地表形变分析的精度降低。Ferretti[12]等人提出永久散射体技术,以多幅SAR 复图像为研究基础,选取幅度高度稳定性的像素点作为PS 点,该方法利用幅度稳定性的估计来代替对相位稳定性的估计,即幅度离差法,且该法需要至少20 幅SAR 图像,某个像素点的幅度离差值(ADI,Amplitude Dispersion Index)如式(1)所示。
其中,σA和mA分别表示该像素点在N幅图像中的幅值标准差和均值。设置幅度离差指数阈值DT,选择满足条件为DA≤DT的像素点为高相干点[13],即可实现高相位质量的像素点选择。DT的取值范围一般为0.10~0.25。
对地基SAR 在重庆万州九道拐获取的30 幅SAR 复图像进行幅度离差法高相干点选择,首先计算时序图像中每一个像素点的幅度离差值,结果如图4(a)所示,设置幅度离差指数阈值为0.25 时,仅能筛选出23164 个高相干点,结果如图4(b)所示,可以直观看到所选取高相干点的数量很少,不利于地表形变分析。
因此在地基SAR 领域,针对植被边坡场景进行形变测量时,采用幅度离差法选取高相干点,其高相干点的数量与质量可能不再满足于形变测量的需求。
3 StaMPS方法
2006 年,Hooper[6]等人提出StaMPS 方法,用于非城镇区地表形变的监测。传统的StaMPS 方法应用于星载SAR 选取PS 点,通过设置幅度离差指数阈值DT选取候选PSC 的初始集合,基于干涉相位的空间相关性特征分析这些像素点的相位稳定性,识别出高相位质量像素点[14-15]。
StaMPS 方法中首先利用幅度离差法获取PSC集合。由Hopper等人的研究表明,设置幅度离差指数阈值DA<0.4时,所选点中会包含大量噪声点,但也有PS点存在[16]。根据式(1)计算所有像素点的幅度离差指数,设置幅度离差指数门限DT=0.4,若像素点满足DA<0.4,则被选为候选PSC,图5 为获取的候选PSC图。
然后基于像素点的相位进行空间维滤波,对滤波后的干涉相位进行相关系数γ估计,图6 为PSC集合的相干系数图,从图中可以直观的看到,PSC集合中存在大量相关系数在0.8 以上的高相干点,通过设定合理的相关系数门限选择出高相干点集合。
其中ω1和ω2分别代表一个像素点为PS 点或非PS点,对于具有低相关系数γ<0.3 的像素点,可以认为p(γ|ω1)≈0,因此有:
分别在式(2)等号左侧积分采用实测数据获取的PSC,对右侧积分利用仿真106个具有随机相位的复像素点exp(jR),然后通过计算这些像素点的相关系数值,就能估计出一个α(k)。非PS点的占比为:
这样,将q和α(k)代入上式,就可以求出相关系数门限。γ反映的是像素点相位的稳定性,通常会随着的增加而降低,用最小二乘法拟合出二者之间的线性关系:
其中k是一个常数,基于最小均方准则可以确定最佳的k,从而在PSC 集合中选择相关系数满足条件的作为高相干点。
如图7 所示,(a)为根据式(2)得到的PSC 集合与非PS 集合概率密度曲线,(b)为相关系数门限与幅度离差均值曲线及拟合曲线,可以看到相关系数的门限很低,过低的门限会将一些低相干像素点误选为高相干点。
图8(a)为StaMPS 方法选取的高相干点选择结果图,可以从图中看到相比于幅度离差法,StaMPS方法可以选择出更多的高相干点,但也明显有许多相干系数较低的像素点被误选为高相干点;接着分析高相干点的质量,根据差分干涉的基本原理,高相干点的干涉相位△φ的主值范围为[-π,π),图8(b)为高相干点的干涉相位图,可以看到图中存在许多相位值大于0 rad的像素点,由此考虑仿真数据与实测数据存在差异性,而造成相关系数门限过低(图7(b))将一些伪PS 点选入,而这些被误选的点最终会影响到地表形变分析的结果。
4 改进方法
在使用传统的StaMPS 方法对地基SAR 获取的影像进行高相干点选择实验时,考虑到仿真数据与真实数据存在差异性,会给地表形变反演结果造成较大误差。因此本文提出改进的StaMPS方法,该方法应用于地基SAR 系统时,能有效的提高在植被边坡场景选择高相干点的数量,保证了地基SAR 的形变测量精度,处理流程图如图9所示,其中红色框为基于传统的StaMPS方法的改进点。
1)像素点分类
本文利用实测数据来获取非PS集合,以消除仿真数据与实测数据差异性带来的较大误差,实验中利用幅度离差法对所有像素点进行分类,设置幅度离差指数阈值DA<0.4得到PSC集合,DA>0.6得到非PS集合,该阈值设置由经验而来。
2)DS点引入
2011 年,Ferretti[7]提出SqueeSAR 方法,将选取的PS 点和DS 点进行联合处理以增加相干点的数量,解决了稀疏植被覆盖地区形变信息提取的难题。SqueeSAR 技术主要由PS 点预处理、DS 预处理和二者联合处理三个步骤组成,其中DS 点的预处理为算法重点。
在探测DS 点时,采用Kolmogorov-Smirnov 算法(简称KS 算法)来为每一个像素点确定同质像素(SHP)集合,该算法是一种非线性检验统计方法,基于两个数据集分布函数差值绝对值的最大值。首先划定7×7的矩形窗,利用KS算法获取中心像素点的同质像素集合,假设像素点X1和X2的累积分布函数分别为(x)和(x),两个累积分布函数的最大差值DN可以表示为
DN的累积分布函数可以表达为
KS算法通过度量差值D超过临界值t的概率来确定像素点X1和X2是否符合同一分布[17]。若该中心像素点的同质像素数目多于设置的数目,则将其定义为DS点。
确定DS 点之后,再利用每个点的同质像素集合逐点估计相位时间序列,并取代像素点原来的相位,最后利用新相位计算DS 点的相干系数,设置相干系数门限0.85,将大于该阈值的点重新选为PS点,从而得到PS点集合2。
最后将PS 点集合1 和PS 点集合2 作为最终所选取的PS点集合。
对比常规方法,改进的StaMPS方法利用实测数据来获取非PS集合,一方面可以实现消除因数据差异性而带来的误差,另一方面通过引入DS 选择技术可以实现进一步提高高相干点选择的数目。
5 实测数据处理与分析
5.1 实验结果
为对比改进的StaMPS 法与常规方法的选取效果,本文进行了基于地基SAR 影像的高相干点选取实验。图10(a)为PSC 和非PS 集合的概率密度曲线,图10(b)为幅度离差均值和相关系数门限曲线及其拟合曲线,图11 为改进后StaMPS 方法选取高相干点的结果图。
根据图7 和图10 对比分析,可以看到改进的方法有明显提高PSC 集合的相干系数和相干系数门限,随着相干系数门限的提高,可以有效的保证所选像素点的相干性;由图4(b)、图8(a)和图11(a)三种方法选出的高相干点分布图与实验区域的光学照片图1对比分析,可以看到三种方法均能识别出光学照片中存在的崖壁、山路等高相干点,由此可以得到利用三种方法进行高相干点的筛选是可行的,另外所选高相干点分布效果StaMPS 方法最佳,改进的StaMPS 方法次之,幅度离差方法最差,但是StaMPS方法选取的高相干点存在许多明显相干系数较低的像素点被误选为高相干点;另外StaMPS方法和改进的StaMPS方法根据图11(b)中的干涉相位图可以直观看出,图像中大部分高相干点的相位在0 rad附近,对比分析图8(b)可以得到改进方法选取的高相干点的相位质量更能保证形变测量的准确可靠性。
5.2 实验结果分析
对于地基差分干涉测量技术而言,高相干点选取的数量、质量等均与地表形变结果分析的准确性息息相关,因此本文将从高相干点选择的数量和质量两个方面来对比幅度离差法和改进前后的StaMPS方法。图4、图8和图11所示分别为这几种方法的高相干点选择结果,分别称为集合A、集合B和集合C。
首先从高相干点的数量来看,对于万州九道拐场景的30 幅雷达图像,采用0.25 的幅度离差门限时,集合A 中有23164 个高相干点;采用传统的StaMPS 方法,集合B 中有104041 个高相干点;采用改进的StaMPS 方法,集合C 中有69505 个高相干点,包括4882个DS点。由于相关系数门限的提高,相比于StaMPS方法,改进方法选取的高相干点数量会存在减少一些。
大气相位误差是地基SAR 系统的主要测量误差源,其与温度、湿度、气压等气象参数密切相关,对于不同时间获取的两幅雷达图像,由于大气条件的改变,会导致大气折射率变化,从而引入不同的传输延迟。在获取差分干涉相位图时,对于每一个散射体,其差分干涉相位中均存在由大气折射率变化所带来的大气相位。
选择实验数据中的第1 幅图像为主图像,其他图像为辅图像,可以分别获取29 幅干涉相位图,以IM()k表示第k幅干涉相位图(IM,Interferometric Map)。图12 中(a)和(b)为其中的两幅干涉相位图IM(7)和IM(20),相应的时间基线为25 分钟和120 分钟。可以看出随着干涉相位图的时间基线的增加,干涉相位图中很多像素点的相位随着斜距和方位角发生缓慢的改变,即干涉相位呈现出较强的空变性,这主要是由大气相位导致的。而采用传统的大气相位随斜距变化模型[18]进行处理就可以精确补偿大气相位带来的相位误差。
根据上述理论分析,本文对比了三种方法大气相位补偿后的相位标准差σ1的分布情况和短时间基线干涉相位图相位偏差的标准差σ2,根据这两个指标对三种方法的高相干点相位质量进行评估,如图13、表2和表3所示。

表2 高相干点相位标准差分布Tab.2 Distribution of phase standard deviation of high coherence point
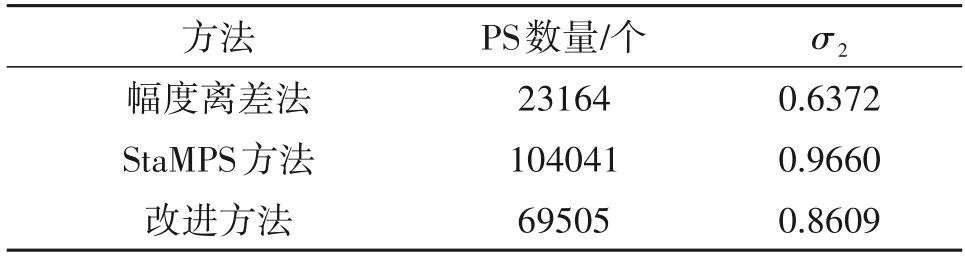
表3 实验参数Tab.3 Experimental parameters
图3 是时间基线最短(5 min)的两幅SAR 复图像生成的干涉相位图,由于时间基线很短,可以认为此时间段内该场景未发生形变,且大气相位的影响也较小,因此所有高相干点的干涉相位应该都接近于0,为了评判所选高相干目标点的准确性,本文利用大气相位补偿后的相位标准差和短时间基线干涉相位图相位偏差的标准差来看高相干点的相位偏差分布,标准差就代表了相位的偏差程度,其值越小代表所选高相干点相位越稳定,其中标准差的计算公式为:
式中:xi为高相干点在N-1 幅差分干涉图中的干涉相位经解缠和补偿后得到的相位序列或短时间基线干涉相位图的相位偏差值,μ为高相干点在N-1幅差分干涉图中的干涉相位经解缠和补偿后得到的相位序列平均值或相位偏差平均值。
图13 显示了高相干点集合A、集合B 和集合C相位标准差的分布情况,其中(a)为这三个高相干点集合相位标准差的概率密度曲线;(b)为对应的概率分布曲线。可以看出,三条概率密度曲线存在一定的差异,说明在不同的标准差区间内的高相干点占比不同;对比三条概率分布曲线,标准差小于0.8 rad 的高相干点占比分别为89.53%、47.13%和60.09%。当雷达系统工作在Ku 波段(工作频率为16.02 GHz),0.8 rad的相位标准差对应着1.192 mm的形变测量精度。如果以0.8 rad 的标准差作为高相干点相位质量的评价准则,对比三种方法,幅度离差法可以选择出更多的像素点,本文方法次之,StaMPS方法选择最少。
表2所示为这三个高相干点集合相位标准差的统计与对比结果。由于集合A、集合B 和集合C 中高相干点的数量不同,虽然集合B 中标准差小于0.8 rad的PS点数量较多,但占比也较小。
接着计算高相干点在短时间基线干涉相位图中相位偏差,其值如表3所示。
由表3中PS数量可以看到,改进前后的StaMPS法较幅度离差法更适合植被覆盖区域的高相干点选取;另外由于改进方法提高了相关系数门限阈值,所选取的高相干点较传统的StaMPS 方法减少了,但是由表3中的标准差可以看出,改进方法选取的高相干点数量上虽减少了一些,但高相干点的短时间基线干涉相位图的相位偏差的标准差明显降低,因此可以判定剔除的点是误选点。
根据图8(b)和图11(b),可以直观看出传统的StaMPS 方法和改进后的方法所选取的高相干目标点经过大气相位补偿后的相位有明显差异,改进方法选取的高相干点减少了相位误差大的点,由此可以得到改进方法提升了高相干点的相位质量。
综合来看,对于九道拐这种植被覆盖区域的边坡场景,采用改进的StaMPS 方法,相比于常规方法,在保证一定的相位质量的前提下,可以显著提高高相干点的数量,有利于地表形变分析的准确度。
5.3 形变测量结果
最后根据地基SAR 差分干涉测量原理,计算高相干点的形变相位,图14为形变测量结果。由图可以看到,监测区域在2020 年5 月24 日0 时~3 时的监测时间内,并未发生较大形变。目前监测场景区域无其他形变测量设备,因此对于雷达形变测量结果无法得到进一步的验证。
6 结论
在地基差分干涉测量技术分析中,为保证形变测量的准确可靠性,选取数量和质量均满足的高相干目标点是关键。本文提出一种适用于地基差分干涉雷达面向植被山体边坡这类复杂监测场景的改进的StaMPS高相干点选择方法,解决了常规高相干点选择方法在地基SAR 应用于有植被覆盖区域进行常规连续观测时,无法兼顾高相干点的数量和质量的难题。采用本文方法与常规方法,对一典型植被山体边坡的30 幅时序SAR 复图像分别进行了实验,对比分析了选取出的高相干点的数量和质量,验证了本文方法的适用性,为地基SAR 在植被山体边坡类型的监测场景获取数量和质量均满足地表形变分析要求的高相干点提供了有效支撑。
