二维空间中一类Boussinesq方程组的结构稳定性

石金诚，肖胜中

(1. 广州华商学院 数据科学学院，广东 广州 511300；2.广东农工商职业技术学院 科研处，广东 广州 510507)

近年来，许多学者开始研究偏微分方程的解对系数的收敛性或连续相依性问题，这类问题称为偏微分方程解的结构稳定性。传统的稳定性主要是研究解对初始数据变化的连续依赖性。然而，越来越多的学者认为连续依赖性的研究不能只局限于初值条件，还应该包含系数、模型本身的边界条件等，这也是我们讨论的结构稳定性。因为我们想知道，方程的一个小改变或者系数的微小变化是否会对方程的解造成巨大影响。在AMES和STRAUGHAN[1]的专著中系统地研究了这种结构稳定性。在实际中，无论是数据测量还是建立模型的过程中都不可避免地存在误差，一个微小的误差是否会导致解的急剧变化，这对后续研究至关重要，所以研究解的结构稳定性是有意义的。

多孔介质中流体方程组的解的性态研究已经成为数学与力学领域的热点问题。现有的研究主要集中在Brinkman、Darcy和Forchheimer方程组的模型上。NIELD和BEJIAN[2]、STRAUGHAN[3]的书中广泛地讨论了多孔介质中的这些模型, 得到多孔介质流体方程组在不同条件下的解的性态。部分学者研究了多孔介质中的Brinkman、Darcy、Forchheimer方程以及其他多孔介质方程的Saint-Venant原则，例如文献[4]得到了多孔介质中的流体方程组的空间衰减估计结果。更多的文献研究了多孔介质中的流体方程组的结构稳定性, 得到了一些连续依赖性与收敛性的结果(见[5-12])。特别地,文献[13-20]取得了一些新的结果。这些文献集中研究了Brinkman、Forchheimer、Darcy类方程组的结构稳定性，对其他类别的非线性方程组，由于非线性项的处理难度大，使得研究它们的结构稳定性较少，特别是含有Boussinesq非线性项流体方程组。

在文献[16]中, 作者研究了三维空间中的一类双扩散的流体方程组的结构稳定性。该方程组由动量守恒方程、能量守恒方程以及溶解度守恒方程组成。在构建动量守恒方程的过程中采用了Boussinesq逼近。本文继续研究该方程组的结构稳定性，讨论二维空间中的方程组

(1)

其中：ui表示速度，p表示压强，T表示温度以及C表示溶解度。gi(x)和hi(x)表示引力函数,为了计算方便，假设gi(x)满足|g|≤1以及hi(x)满足|h|≤1。f(x)是连续可微的函数，Lf(T)为化学平衡项，Δ为拉普拉斯算子,λ、L和k均是大于零的常数，λ是Boussinesq系数，L为化学平衡系数，k为化学反应率。在文献[2-3，21]中均有该方程组的详细介绍。方程组(1)在Ω×[0,τ]区域内成立，其中Ω是R2中有界单连通的星形区域,τ是给定的常数且0≤τ<∞。

给定的边界条件为

(2)

其中，k1、k2是大于零的常数。此外，初始条件为

ui(x,0)=ui0(x),T(x,0)=T0(x),

C(x,0)=C0(x),x∈Ω

(3)

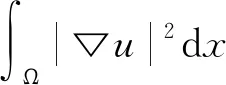
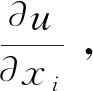
1 先验估计

在本节中将推导出一些有用的引理。

引理1对于速度的梯度，有如下估计：

(4)

其中：TM、CM是大于零的常数，n1(t)是单调递增且大于零的函数, |Ω|是Ω的体积。

证明在方程组(1)的第1个方程两边同时乘以ui,并且在Ω上积分，由散度定理和式(2)，可得

(5)

对于式(5)，由Schwarz不等式，可得

(6)

运用[22]中的式(4)、(5)和(18)的结果，可知

(7)

(8)

(9)

其中：TM、CM是大于零的常数，n1(t)是单调递增且大于零的函数。

联合式(6)～(9),可得

引理2对于速度ui，有如下估计：

(10)

其中：

证明由方程组(1)的第1个方程，可得

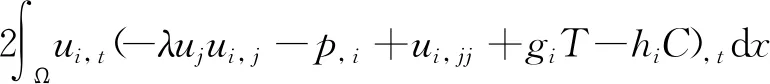
(11)

由文献[22]中的式(20)，有如下的二维Sobolev不等式成立：

(12)

其中，r为大于零的常数。式(12)中取H=ui,t，有

(13)

联合式(11)和(13),可得

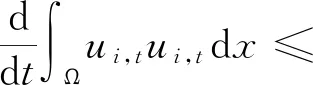
(14)

联合式(4)和(14)，可得

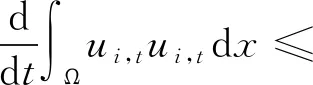
引理3对于温度和溶解度，有如下估计：

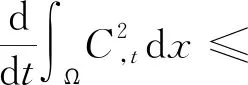
(15)

(16)

证明由散度定理和方程组(1)的第4个方程，可得

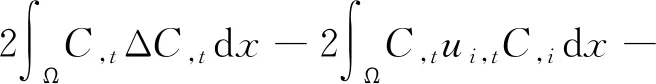
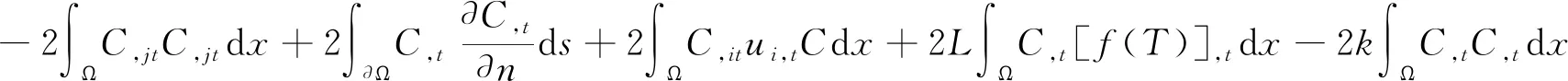
(17)

由于T有界，且f∈C1,则

f′(T)≤d2

(18)

其中，d2是大于零的常数。对于式(17)，由Hölder不等式、式(2)和(18)，可得

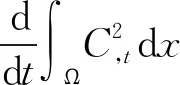
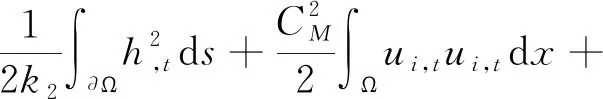
(19)

同理，可得

(20)

引理4对于能量函数，有如下估计：

(21)

其中

证明定义能量函数F(t)如下：

联合式(10)、(15)和(16),可得

(22)

其中

式(22)可写为

(23)

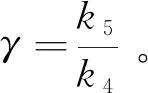
(24)

求解式(24)，可得

(25)

则有

F(t)≤n3(t)

将式(21)代入式(4)，可得到如下结果:

引理5对于速度的梯度，有如下估计:

(26)

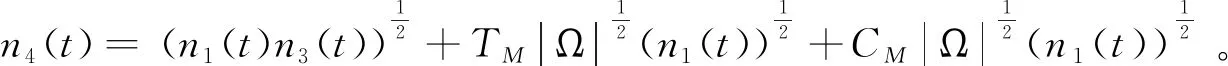
2 解对Boussinesq系数的连续依赖性

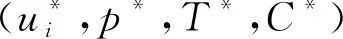
(27)

边界条件为

(x,t)∈∂Ω×[0,τ]

(28)

此外，初始条件为

ωi(x,0)=0,θ(x,0)=0,S(x,0)=0,x∈Ω

(29)

将得到以下主要结果：

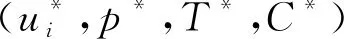
(30)

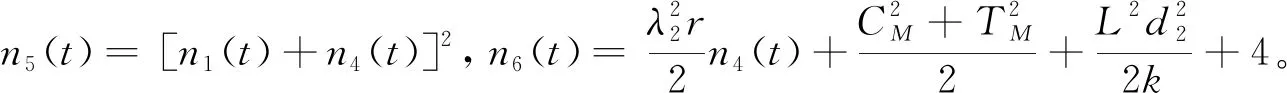
证明在方程组(27)第1个方程的两边同时乘以ωi，并在Ω上积分，由式(12)和Hölder不等式，可得

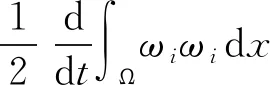
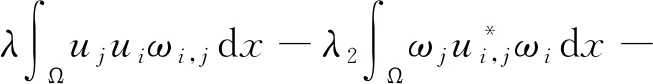
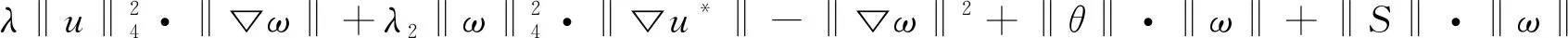
‖θ‖·‖ω‖+‖S‖·‖ω‖

(31)

其中，ε1、ε2是大于零的任意常数。

式(31)取ε1=2,ε2=2，由Hölder不等式、式(9)和(26)，可得

(32)

在方程组(27)第3个方程的两边同时乘以2θ，并在Ω上积分，由散度定理和式(28)，可得

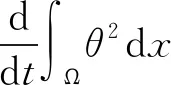
(33)

由Lagrange 中值定理，可得

f(T)-f(T*)=θf′(ξ),ξ∈(T*,T)

(34)

同理，在方程组(27)第4个方程的两边同时乘以2S，并在Ω上积分，由散度定理、式(18)、(28)和(34)，可得

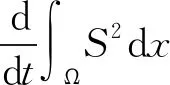
(35)

联合式(32)、(33)和(35)，可得

(36)

求解式(36)，可得

(37)

3 结论