横向摆杆式明渠测流方法在矩形渠道中的应用研究

范 恬，周义仁

（太原理工大学水利科学与工程学院，太原030024）

0 前 言

灌区量水技术是农业灌溉中的一项关键技术，灌区精准测量的意义在于为合理分配水资源、提高灌溉用水效率提供可靠的计量依据，因此发展结构简单、使用方便、测流精度高的量水设施显得尤为重要[1-3]。

目前我国灌区输水渠道多是明渠，传统的明渠测流理论有水工建筑物法、坡降-水力半径法、流速面积法等[4]，在这些理论基础上发展出水工建筑物量水、特设量水设施量水、流速仪量水、仪表量水等常用的量水方法。水工建筑物量水指利用跌水、渡槽等建筑物进行量水。此方法经济便捷、水头损失小，但对建筑物及渠道的要求较高；特设量水设施量水指利用量水槽、量水堰等设施进行量水，此方法精度高，数据易读取，但水头损失较大；流速仪量水是指利用流速仪测量标准渠道断面的特征点流速，推算过水断面面积及平均流速并利用流速面积法来计算流量的方法，此方法测量精度较高，但测流及计算过程繁琐；仪表量水是指利用压差式流量计、电磁流量计、超声波流量计等二次仪表进行量水，此方法精度较高，量测直观，但其价格较高，适用范围不广[5-8]。在上述测流方法的基础上，国内外学者对明渠测流方法进行了更多探索，为明渠测流提供了新思路。刘力奂[9]等从泵站中的拍门装置受到启发，提出了一种利用细长板开启角进行测流的新型测流方法，通过理论分析得到了细长板开启角度与明渠均匀流流量之间的方程式；郭志华[10]对细长板进行优化，设计了一种板柱复合式流量量测装置，在测角板之前增加光滑实心半圆柱体用来固定支撑，通过理论推导及量纲分析得到了测角板偏转角度与过水断面流量之间的经验关系；石先德[11]提出利用圆柱形测流摆杆进行测流，与以往的测流板相比，对水流的扰动更小，水头损失较小。此类测流方法均将竖直测流摆杆（板）布置在渠道过水断面中垂线上，利用这一测线上的摆杆（板）转动角度与过水断面流量之间的对应关系（θ-Q）来进行测流。

为了进一步提高测量精度，本文提出一种在多条测线上进行测流的方法。此方法将渠道过水断面划分为多个流层，利用横向摆杆在不同流层进行多次测量，通过分析摆杆转动角度与过水断面流速之间的对应关系（θ-v）并采用流速面积法来计算过水断面流量，其测流误差小于5%，测流精度高，可以实现自动化测流，在矩形渠道中具有广阔的应用前景。

1 测流装置介绍

该横向摆杆式明渠测流装置由固定结构、传送结构、摆杆结构及控制系统组成，其具体机械结构如图1所示。该装置适用于斗、农渠，在使用时首先将固定结构中的支架放置在渠道两侧，调整螺纹底座的高度使得横向支架保持水平；调整支架位置使得传送结构中的滑轨紧贴渠道边壁；打开水位传感器测得当前水位，在控制系统中输入划分流层数量；启动步进电机使得螺纹丝杆转动后即可控制摆杆在不同水深处进行自动测量。

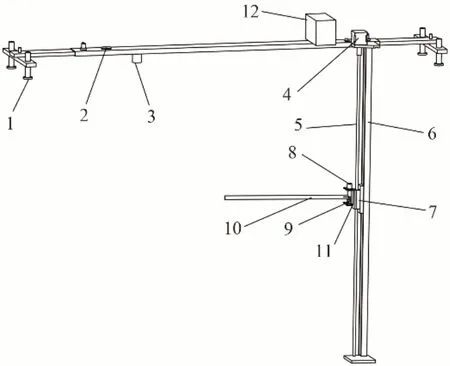
图1 装置机械结构图Fig.1 Mechanical structure diagram of the device

2 测流原理

横向摆杆式明渠测流装置是基于圆柱绕流模型以及流速面积法来计算渠道流量的。圆柱绕流是水力学中基本而又复杂的流动，当流体流过物体，或物体在流体中运动时，通常会受到阻力作用，此时物体所受到的力称为绕流阻力[12]。绕流阻力的表达式为：

式中：CD为绕流阻力系数；A为物体与流速垂直方向的迎流投影面积，m2；ρ为水的密度，kg/m3；v为水流流速，m/s。

在本装置中，当横向摆杆淹没在水流中时，竖直方向上受到自身重力G、浮力Ff及弹簧槽对转轴的支持力FN3 个力，如图2所示。

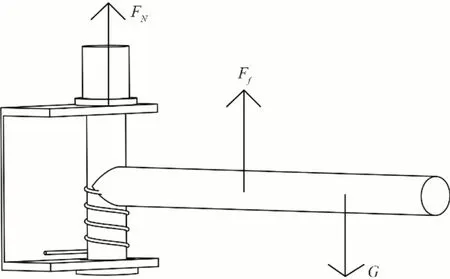
图2 竖直方向受力图Fig.2 Vertical stress diagram

此时竖直方向上横向摆杆在此3个力的作用下处于静力平衡状态。即：

整理得：

由式（3）可以计算出弹簧槽对横向摆杆的支持力FN。

当水流冲击横向摆杆时，横向摆杆带动转动轴旋转一角度θ，此时摆杆在水平方向上受到扭转弹簧对摆杆的弹力T、水流冲力P及弹簧槽与转动轴之间的摩擦力f，如图3所示。

图3 水平方向受力图Fig.3 Horizontal stress diagram

此时对转动轴轴心取矩，整个摆杆达到力矩平衡。根据力矩平衡原理，有：

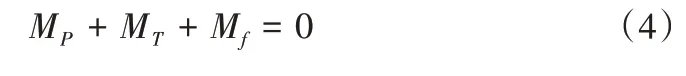
即：

式中：LP为水流冲力作用点距离转动轴轴心的距离，m；E为扭转弹簧的弹性模量，MPa；d为弹簧线径，mm；D为弹簧中径，mm；m为经验系数，常取值为3.667×106，（°）；θ为摆杆的转动角度，（°）；n为弹簧有效圈数；μ为摆杆转动轴与弹簧槽接触面之间的摩擦系数；R-r为摩擦接触面半径差，m。

由绕流阻力公式（1）可知，式（5）中的水流冲力P可用断面流速v表示，扭转弹簧产生的扭矩可用转动角度θ表示，因此上式中仅有摆杆转动角度θ与流速v为未知量，由此可知断面流速v与转动角度θ之间存在对应关系。依据量纲分析中的π 定理，推导出断面流速v与转动角度θ之间的对应关系如下：

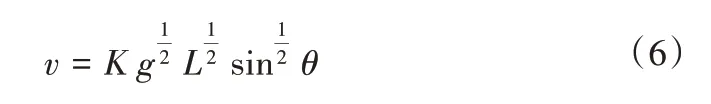
式中：g为重力加速度，m/s2；L为摆杆长度，m；系数K与渠道底坡i、渠道糙率n等相关参数有关，可通过线性分析得到K的值。

由上述公式（6）逐层测量不同水深的断面流速vi，并利用流速面积法计算断面流量，则整个过水断面流量计算公式为[13]：

3 试验方案

为了探究该装置的测流精度，在太原理工大学水利科学与工程学院的水流大厅中的矩形渠道上对该横向摆杆式明渠测流装置进行物理实验。

此次实验中选取了8 个工况，依次在流量为30、40、50、60、70、80、90、100 m3/h 时进行测流实验。实验中所用渠道为矩形渠道，其过水断面上流速分布关于中垂线具有对称性，因此选取渠道断面的1/2 面积作为测量区域。在测量时将测量区域水平划分为5 个流层，分别在0.1、0.3、0.5、0.7、0.9 倍的水深处测量过水断面流速vi，并利用公式（7）将各个所测得流速vi与该流层面积Ai的乘积相加即可得到测量区域的流量[14]，则整个渠道的过水断面流量为测量区域流量的2倍。

4 模拟仿真

为了测试该横向摆杆式测流装置的测流性能，探究横向摆杆装置对渠道内流场的影响，本次研究运用FLUENT模拟软件对该测流装置的测流过程进行模拟仿真，通过对比物理实验结果来验证该模拟仿真的准确性[15]。

4.1 几何建模与网格划分

本文中所实验及模拟渠道的主要参数为：渠深0.3 m，渠宽0.27 m，渠道底坡为1/1 000。模拟时渠道模型沿水流方向长度设置为2 m，入口处1 m 的范围为稳流池，用以确保水流从入口处平稳过渡到矩形渠道中。该横向摆杆式明渠测流装置位于距离入口处1.25 m 处，横向摆杆的高度设置在0.7 倍的水深处，模型图如图4所示。

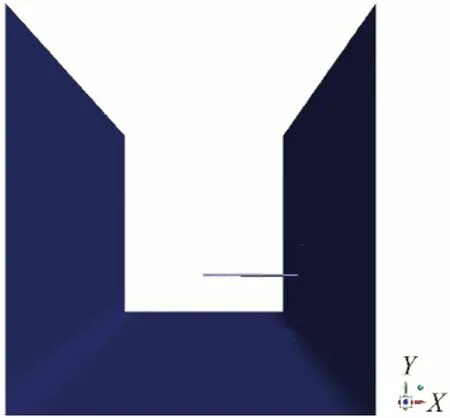
图4 模型示意图Fig.4 Model diagram

CFD 计算中采用的网格可以大致分为结构化网格和非结构化网格两大类[16]。结构化网格数据结构简单、生成速度快、网格质量好，但使用范围比较窄；非结构化网格是生成速度慢，但是适应性较强，对细节的捕捉较好[17]。采用结构化网格与非结构化网格相结合进行求解，可以减少计算时间，提高模拟精度。本文所涉及到的渠道模型全长2 m，对该模型进行区域划分，入口附近1 m 的范围及出口附近0.5 m 的范围均设置为结构化网格，摆杆上下游0.25 m 的范围内均设置为非结构化网格。设置全局网格最大尺寸为0.02 m，摆杆表面局部加密，设置单元尺寸为0.01 m，整个模型中网格总数约为11 万个，具体网格划分示意图如图5所示。

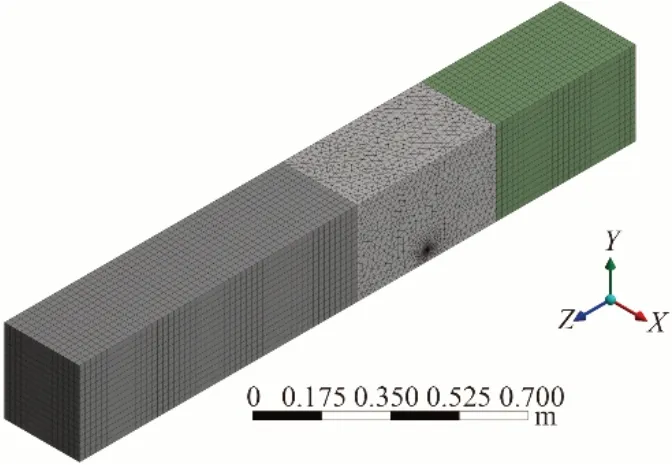
图5 网格划分示意图Fig.5 Schematic diagram of meshing

4.2 边界条件及求解方法

基于该模型为明渠流动，采用VOF 自由液面模型及标准k-ε湍流模型的基础上，为了使模拟更为精确，渠道顶部设为压力入口；上游进口设置为速度入口；下游出口设置为压力出口；摆杆以及渠道壁面全部设为固壁边界[18]。在进行初始化时使整个计算域中最开始时充满了空气，上游进口断面处水的体积分数为1，当水流从入口处进入渠道中时，通过VOF方法进行迭代，自动生成水气交界面。

FLUENT 模拟软件提供了压力基求解器和密度基求解器两种，本系统采用压力基求解器即可。此次模拟在算法选择上选择PISO算法，运行计算时，每20步保存一次[19]。

5 结果分析

5.1 测流精度分析

矩形渠道中竖直方向上的流速分布并非处处相等，因此测量流层不同，摆杆转动角度也不相同。为分析测流公式v=的测流精度，利用ORIGIN 软件将摆杆转动角度θ与流速v之间的关系进行线性拟合，如图6所示。

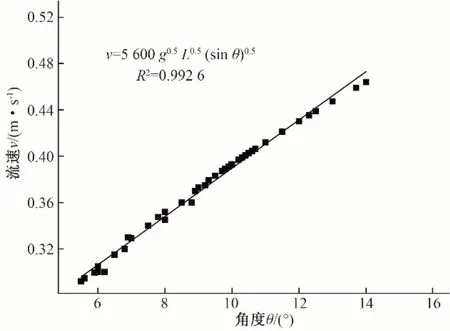
图6 摆杆转动角度θ与流速v之间的线性关系Fig.6 Linear relationship between swing rod θ rotation angle and flow velocity v

由图6 可以发现，各点分布于一条直线上，流速v与摆杆转动角度θ之间呈现正相关的线性分布关系，其线性相关系数为0.992 6，说明该测流公式可以精确地反应流速v与摆杆转动角度θ之间的关系。

此次实验中用横向摆杆式明渠测流装置与电磁流量计同时测量渠道内的瞬时流量，其测量结果如表1所示。

由表1可以看出，该横向摆杆式测流装置的实测流量值与电磁流量计测量结果接近，平均测量误差为2.31%，满足《取水计量技术导则》中在明渠输水时取水计量误差应≤±5%的规定，测量精度较高。

表1 测量流量与理论流量的对比及误差Tab.1 Comparison and error between measured flow and theoretical flow

5.2 水面线分析

为了探究横向摆杆测流装置对渠道内水面线的影响，通过对测流过程进行模拟仿真来分析各个工况下的水面线变化情况。

此次模拟通过对流量为30、40、50、60、70、80、90、100 m3/h 的8 个工况进行模拟仿真，得到各个工况下的水位，并与实验中的水位进行比较，结果如图7所示。

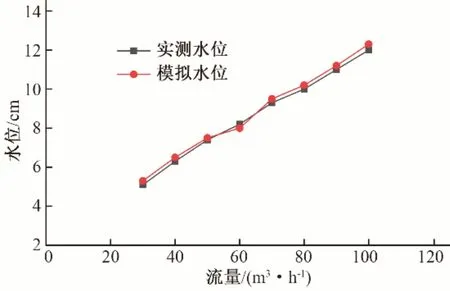
图7 模拟水位与实测水位的对比关系图Fig.7 Comparison between simulated water level and measured water level

由图7 可知，模拟结果与实测水位基本相同，说明利用FLUENT 对明渠流动进行模拟仿真可以得到与实际相符的结果，模拟结果与实验结果相互验证，证明了物理实验与模拟仿真的准确性。

图8 是当流量为100 m3/h 时在不同时刻渠道中的水面线变化情况，从上向下依次为计算0 步、300 步、600 步、800 步、1000 步、1400 步时的水面图，图中蓝色区域为空气，红色区域为水流，红蓝相间区域为气液交界面。

BIM技术应运而生，上海中心、鸟巢都成功“试水”，但是，BIM在中国的建筑业市场的应用依然相对狭窄，住房和城乡建设部发布的《关于2017年二季度全国工程质量安全提升行动进展情况的通报》中提到：在部分地区推动工程技术进步工作进展较为缓慢。

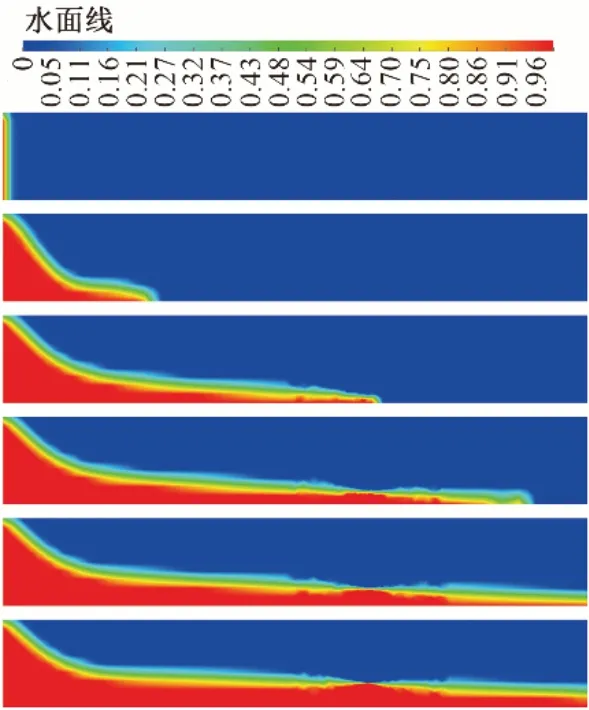
图8 工况为100 m3/h时的水面线变化情况Fig.8 Change of water surface profile under working condition of 100 m3/h

由图8可知，该工况下气液交界面明显，随着水流的不断流入，渠道中水流场区域不断增加，水位逐渐上升。当水流接近摆杆时，由于受到摆杆对水流的扰动，水面线略有下降，在水流远离摆杆的过程中，摆杆对水流的扰动越来越小，因此水面线略微上升，在达到一定高度后水面线逐渐趋于稳定，这与实验现象相符。从模拟结果图中可以直观地看出，摆杆装置对水面线的扰动较小，不会改变水流流线。

5.3 速度场分析

为了探究矩形渠道过水断面流速变化规律及摆杆装置对渠道中过水断面流速的影响，此次模拟以各工况中摆杆尾端所处的竖直断面为研究对象，通过模拟仿真来分析各个测流断面中的流速分布情况。如图9 所示为在工况为40、60、80、100 m3/h时渠道过水断面中的流速分布情况。

图9 各工况下的流速分布情况Fig.9 Velocity distribution under various working conditions

由图9可知，在矩形渠道中过水断面的流速分布关于中垂线具有对称性，由于摆杆对水流的扰动作用，水流在流经摆杆时产生局部绕流现象，导致摆杆附近的流速突然减小，摆杆壁面的水流流速近乎于零。随着流量的增大，渠道内的液面高度逐渐升高，过水断面面积增大，渠道内的过水断面流速也逐步增加。渠道断面内的横向流速分布规律为：沿渠道中垂线至渠道侧壁，流速逐渐减小，渠道侧壁附近区域的流速急剧变化，侧壁上的流速为零。渠道断面内的垂向流速分布规律为：随着水深的增大，垂向流速基本呈现先增大后减小的趋势，渠底流速约为零，最大流速位于水面线以下某一位置，这与实际流速分布规律相符。从模拟仿真的结果可以看出摆杆对过水断面流速的影响范围仅在摆杆区域附近，渠道内其余区域不受到摆杆的扰动，产生的水头损失较小。

6 结 语

本文通过对横向摆杆式测流装置进行物理实验及模拟仿真，并对实验数据和模拟结果进行对比分析，得到了以下结论：

（2）模拟仿真的结果表明：渠道来流过程中水面线在接近摆杆时呈下降趋势，在远离摆杆时呈上升趋势，最终趋于稳定；渠道断面中横向水流流速中间大，两侧小，垂向最大流速位于水面线以下，这与水力学原理及实验现象相符合，说明利用FLUENT 中的VOF 两相流模型和标准k—ε湍流模型对横向摆杆式测流装置进行模拟仿真是可行的。

（3）本文基于流速、摆角之间的关系以及流速面积法原理设计了一套横向摆杆测流装置，该装置测流精度高、操作简便、方便携带，为灌区测流提供了一种新的选择，具有良好的应用前景。

（4）通过在实验室进行模型试验可知该横向摆杆式明渠测流装置在流量为30～100 m3/h 的矩形渠道中的测量精度满足规定要求，对于其在实际应用及大型渠道中的使用还有待研究。