基于数据同化的地下水模型不确定性分析

陈 冲，张 伟，邢庆辉，豆沂宣

（1.中国石油大学（北京）信息科学与工程学院，北京 102249；2.中国科学院 西北生态环境资源研究院 冰冻圈科学国家重点实验室/可可托海站，甘肃 兰州 730000）

0 引言

地下水系统模拟已经成为地球科学的基本研究方法，在地球系统科学领域被誉为第二次哥白尼革命［1］，被证明是最有价值和最实用的工具之一［2-3］。地下水模型能够刻画水文过程的整体和局部行为；多次模拟，选择最优的设计；通过情景分析进行情景预测，提出应对策略。围绕黑河中游地表水、泉水和地下水，大量学者利用模型进行了有益探索：陈冲等［4］建立了黑河中游地区地下水模型，并初步分析了上游径流与耕地面积对地下水资源的影响；王旭升等［5］总结了20 年来黑河流域的地下水模型研究，并指出地下水模型应加强与关联过程（地表水、土壤水、水利工程）的集成；程国栋等［6］阐述了黑河流域生态—水文过程集成研究的进展及展望。目前的地下水模型一般基于确定性的参数、边界条件，采用确定性机制来构建模型。然而，由于实际过程的复杂性及非线性因素，导致模型往往存在一定不确定性。正如George 所言，所有关于真实系统的模型都是“错误”的［7］，即模型永远不能完美表达实际系统。地下水模型的不确定性来源一般可以分为：模型数据的不确定性、模型结构的不确定性以及模型参数的不确定性。模型数据的不确定性一般指由于监测误差或者数据缺失导致的不确定性，只能通过提高监测技术和数据收集频率来降低。而模型结构和参数不确定性则来源于建模过程、模型参数标定及验证过程。这些不确定性将对进一步的科学研究以及决策提出等带来诸多麻烦甚至风险。因此在使用地下水模型时，对其进行不确定性分析是十分必要的。

Oberkampf等［8］介绍了用来估计、分析模型中所有类型不确定性的多种方法。Beven［9］于1989 年在对物理模型的适用性进行讨论的过程中，首次提出了对水文模型进行不确定性分析的概念。地下水模型不确定性分析方法主要分为蒙特卡罗（Monte Carlo）法、矩方程法与贝叶斯法三种［10］。虽然MC法是一种被广泛采用的不确定性分析方法［11-15］，但是MC 法的缺点也不容忽视，其需对模型的参数进行大量的采样才能保证算法的正确性和准确性，无法适用于计算消耗大的模型。矩方程法通过随机偏微分方程直接求解模拟结果的各阶统计矩，已在地下水模型不确定性研究中得到初步应用［16-18］。贝叶斯法利用观测资料修正水文地质参数分布，其既可以用于模型参数识别反演［19］，也能够用于对参数进行不确定性分析，其优点是通过更新参数分布，以更加准确的评估模型不确定性。利用贝叶斯法进行地下水模型不确定性分析的研究相对较少［20-21］。数据同化（DA，Data Assimilation）是基于贝叶斯理论的参数更新方法。卡尔曼滤波算法（KF，Kalman Filter）是由Kalman 提出的顺序数据同化算法［22］，其利用观测资料自回归地对模型的状态变量进行更新，并在更新的整个过程中保证状态变量估计值的误差最小。自提出以来，KF算法已被广泛应用于模型参数与状态的估计中。黄春林等［23］基于集合卡尔曼滤波（EnKF，Ensemble Kalman Filter）利用土壤水分观测数据同化了简单生物圈模型（SiB2，Simple Biosphere Model 2），探讨了简单生物圈模型的单点土壤水分同化方案；褚楠等［24］进一步采用双EnKF方法同时估计SiB2模型中土壤水分与土壤属性参数，提高了模型对土壤水分的估计精度。Li 等［25］实现了采用EnKF 同时估计地下水模型的参数与状态变量。Sly 等［26］基于EnKF算法采用SWOT（Surface Water and Ocean Topography）模型的 输出对GHMs（Global Hydrological Models）进行了同化，提升了全球尺度水文模拟的精度。然而，仅有少量研究基于数据同化方法进行模型不确定性分析。例如，Li 等［25］采用了ESMDA（Ensemble Smoother with Multiple Data Assimilation）分析了焉耆盆地水文模型参数的不确定性。

本文基于前期工作中在黑河流域中游构建的地下水模型［4］，拟结合ESMDA 与EnKF 实现地下水模型参数的不确定性分析，探讨ESMDA 与EnKF算法超参数对模型不确定性分析效果的影响，利用算法定量分析地下水模型参数的不确定性、对不同观测数据的敏感性以及不同参数的不确定性范围。

1 研究区域

黑河流域是我国第二大内陆河流域，位于我国西北部干旱区，面积约为14×104km2。流域上游的祁连山区是我国重要的冰冻圈分布区，气温较低、蒸发弱，年平均降水量大于300 mm，丰富的冰冻圈融水与降水是整个流域的主要水源。流域下游为额济纳旗盆地，为典型的大陆性气候，具有降水少（年均降水量为43.7 mm）、蒸发强（年均蒸发量为2 248.8 mm）、日照时间长、昼夜温差大等特性［27］。流域内支流共35 个，由于过度开采及蒸发，绝大部分支流在山前消失，中游主要河流只有黑河干流与梨园河（图1）。黑河发源于祁连山北麓，由东南流向西北，途径青海、甘肃及内蒙古三个省区，最终注入居延海，全长约821 km，水量主要由降水、冰雪融水以及地下水出流组成。莺落峡水文站为黑河出山口径流量观测站，多年（1945—2012 年）平均年径流量约为15.9×108m3，是中游张掖市、临泽县、高台县及下游金塔东部和额济纳旗绿洲等地城市工业、生活用水的主要水源［28］。黑河流域中游（38°38′～39°53′ N，98°53′～100°44′ E；图1）为典型的干旱气候，年降水量稀少（90～160 mm），潜在蒸发量大（2 000～2 500 mm），总面积约9 016 km2［29-30］。河流流出祁连山后，一部分被引入灌溉渠系和供水系统，其余则沿河床下泄，并于沿途渗入地下，补给地下水，黑河在山前冲积扇区损失33%的径流量［31］。长期以来，黑河中游农业生产与下游湿地、尾闾湖等生态环境之间存在着用水矛盾，且由于社会、经济发展和人口的增长，用水矛盾日益突出。

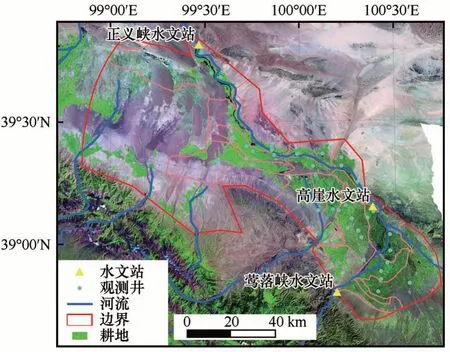
图1 研究区地理位置Fig.1 Study area and observation sites

在前期工作中，我们构建了黑河流域中游的地下水模型，采用了SRTM（Shuttle Radar Topography Mission）的DEM（Digital Elevation Model）数据［32］、土地利用［33-34］、抽水［35］、灌溉［36］、地下水位［37］以及河流径流量数据。将SRTM 90 m×90 m 的数据处理为1 km×1 km 的网格数据对研究区含水层系统进行空间离散化。时间上，将所获取数据（1986 年1 月—2010 年12 月）离散为月时间间隔，采用以每个自然月为一个应力期的非稳定流（暂态流，Transient state）模拟。地下水位数据包括42 口观测井处的观测水位，河流径流量包括莺落峡、高崖及正义峡处观测的径流数据。经过校正（1986 年1 月—2008 年12 月）与验证（2009 年1 月—2010 年12 月），模型对研究区内地下水位及径流量的拟合程度较好，所构建的地下水模型比较真实地反映了研究区地下水系统的情况［4］。

2 研究方法

本文采用ESMDA 与EnKF 结合的方法ESMDA-EnKF 对研究区地下水模型的参数进行不确定性分析。图2 给出了使用ESMDA 算法进行不确定性分析的程序流程。在进行不确定性分析之前，首先要对算法进行初始化，并对模型的参数进行设置，根据给定的概率分布（一般假定为正态分布或者对数正态分布）生成模型参数集合。将模型参数预测值分别输入地下水模型中，计算得到模型输出值；综合地下水模型输出、观测值、观测误差协方差以及参数预测值集合输入ESMDA-EnKF 算法中，从模型输出值和观测值集合计算得到增量场，根据集合中样本的误差统计计算出卡尔曼增益，由增量场与卡尔曼增益计算得到预测结果的更新量，将更新量叠加到初始场得到分析值集合；根据预先算法执行次数判定是否达到程序运行结束条件。

图2 ESMDA-EnKF算法不确定性分析流程图Fig.2 Diagram of uncertainty analysis using ESMDA-EnKF

2.1 集合卡尔曼滤波（Ensemble Kalman Filter）

EnKF 采用蒙特卡罗方法随机产生参数集合，对状态变量进行预测，并根据获取的观测信息对状态变量进行更新，已经有许多文献对其理论和具体算法做了详细的论述［38-39］。此处仅简要回顾一下EnKF的主要的工作原理。

在EnKF 中，定义第t个时刻的参数和状态向量集合为：

式中：X为Nx维状态变量；A为Na维参数向量；B为Nb维系统状态向量；且

则状态变量在第t+1时刻的预报值为

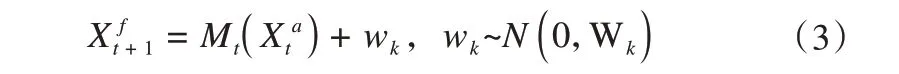
式中：f代表状态变量的预测值（forecast）；a代表状态变量的分析值（analysis）；为第i个状态变量在t+1 时刻的预测值；Mt（•）为非线性模型算子；为t时刻的分析值；wk为期望为0，方差为Wk的高斯白噪声。

在分析步骤（analysis step）中，采用公式（4）对观测数据进行扰动

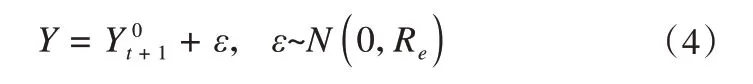
2.2 多重数据同化集合平滑器（Ensemble Smoother with Multiple Data Assimilation）

对ESMDA 算法主要分为3 个方面进行介绍，首先介绍集合平滑器（ES，Ensemble Smoother）；接下来在ES 算法中引入膨胀系数构成ESMDA 算法框架；最后，介绍ESMDA与EnKF算法的结合，并给出伪代码的实现。

2.2.1 集合平滑器（Ensemble Smoother，ES）

EnKF 属于顺序数据同化算法，其根据t时刻状态变量值初始化模型，预测t+1 时刻模型的状态变量，在t+1 时刻利用观测资料对状态变量的预测值进行加权更新，得到当前时刻状态变量的最优估计值，多用于对状态变量进行实时标定，以实现实时模型。然而，ES多用于参数反演以及参数的不确定性分析中，采用所有可用观测资料对参数进行更新。公式如下：

式中：各个符号定义与EnKF中类似。

2.2.2 ESMDA

ES 的本质是将所有时刻的观测资料输入同化算法中进行一次参数更新［40］。然而，正如算法名字所示，ESMDA 在ES 的基础上设定一个算法执行次数，进行多次数据同化，在每个循环中，ESMDA 并不是简单重复了ES过程，而是在每个循环中对观测误差添加了一个膨胀系数αi，并令

式中：Na为循环次数。显然地，αi有许多种取值方式，然而文献［41］指出，随着循环次数的增加而逐渐减小的膨胀系数对于同化效果并无明显提升。因此，在每次循环中，采用相同的膨胀系数。

2.2.3 ESMDA-EnKF

ESMDA-EnKF 在每次循环中采用EnKF 对参数进行更新，其更新公式如下：

第i次循环：

其中，Yall为经过αiRe扰动的观测资料。

ESMDA-EnKF的具体实现如下伪代码所示：

输入：Na，观测资料Oall，Xf，Re

输出：Xa，K，Pa

read（Oall）

fori=1 to Na

Xf’=Xf-mean（Xf）

Yall=Oall+sqrt（αi* Re）

HXf’=HXf-mean（HXf）

PfHT=（Xf’* HXf’）/（N-1）

HPfHT=（HXf’* transpose（HXf’）/（N-1）

K=PfHT/（HPfHT+αi* Re）

Xa=Xf+K *（Yall-HXf）

Pa=Pf-K * PfHT

update（Xf，Pf）；

return（K，Xa，Pa）

2.3 地下水模型

黑河流域中游地下水模型基于MODFLOW（MODular three-dimension finite-difference groundwater FLOW model）构建，MODFLOW 采用有限差分法将时间与空间离散化以解决地下水在三维空间中的流动问题。研究区平面面积约为9 016 km2，采用1 km×1 km 的正方形网格将研究区含水层系统在水平方向上进行空间离散化，离散化之后，研究区在平面上剖分成为132 行×165 列网格（如图3）。研究区内定义为活动单元，研究区外定义为非活动单元。时间上，以每月为一个应力期，每天为一个时间步。研究区边界条件参考文献［42］以及自然边界确定（图3）。由于地下水分水岭的存在，A～E 设置为无水流边界；E 处为正义峡水文站，黑河从此处流出研究区；据调查资料分析，北山地区地下水含水介质与南部祁连山相似，但由于降水稀少，无常年地表径流，地下水含量无法与祁连山区相比较［27］，因此，将D～E 边界假设为无水流边界；由于多种侧向流从南部祁连山流入研究区，导致A～D边界最为复杂，因此，将此边界分为3 段进行定义：如图3 所示，A～B 与C～D 定义为定流量边界条件（第二类边界条件或Neumam 条件），B～C 之间定义为无流量边界。垂直方向上，模型顶部边界为空气—土壤接触面边界，模型底板定义为不透水边界。黑河干支流采用MODFLOW 内的河流（STR，STreamflow-Routing）程序包［43］进行模拟。农业灌溉通过采用地下水补给程序包（RCH，Re-CHarge）［44］在网格上添加补给率实现。蒸散发采用了MODFLOW 内置的蒸散发程序包（EVT，EVapo-Transpiration）进行模拟。机井采用机井程序包（Well）进行模拟。

图3 黑河中游模型概化及边界设置Fig.3 The conceptualization and boundary conditions of the groundwater model

2.4 模型评价

本文采用均方根误差（RMSE，Root Mean Square Error）对模拟结果进行量化评价，方程如下：

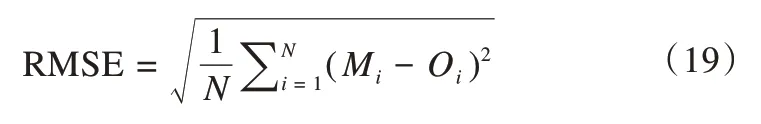
式中：N为观测值总数（观测井个数×应力期个数）；Mi和Oi分别是模型模拟值和观测值。

3 结果与讨论

3.1 算法参数分析

在使用ESMDA-EnKF 算法对地下水模型进行不确定性分析的过程中，算法存在一些超参数直接影响到同化算法对模型参数的更新效果（例如：算法执行次数（即膨胀系数）Na、观测资料数n、参数集合大小N等），因此，本文首先为ESMDA-EnKF确定最优超参数，之后采用算法分析模型参数的不确定性以及模型参数对观测数据的敏感性。

3.1.1 ESMDA执行次数对不确定性分析的影响

ESMDA 采用EnKF 算法对地下水模型参数进行更新，因此，EnKF 算法的执行次数将直接影响模型参数的更新效果。然而，目前尚没有关于执行次数的理论研究，而在文献［41］给出的例子中，分别执行了2次、4次算法以对比同化效果。考虑到计算消耗问题，本节评价了执行1 次、2 次、3 次、4 次En-KF算法后的同化效果（图4）。

图4 不同执行次数对ESMDA-EnKF算法效果的影响Fig.4 Results of ESMDA-EnKF for different iterations

图4 中展示了EnKF 算法执行不同次数后的同化效果，Last iteration 代表采用不同的执行次数时，最后一次执行结束之后的同化效果。由图中可以看出随着EnKF 算法对模型参数的更新，地下水位的RMSE 值逐渐降低，表明地下水位模拟值逐渐接近地下水位的观测值。经过随机采样之后的第一次、第二次参数更新对RMSE 影响较大；第三次及第四次参数更新之后，与第二次参数更新之后的RMSE值相比，变化不大。这表明，使用观测数据对地下水模型参数进行的前2 次更新最为有效，可能是因为：（1）地下水模型的参数采用随机初始化，因此，ESMDA 在随机模型参数的基础上进行的第一次更新力度相对较大；（2）ESMDA 采用了所有时刻的观测数据进行更新，最大程度上利用了观测数据中的信息，因此，能够更加有效且大幅度的更新参数。

3.1.2 观测资料数对不确定性分析的影响

数据同化的目的即是最大限度的融合不同来源、不同时间、空间分辨率的直接、间接观测数据以用于提高模型的估计精度，以获得更加准确的状态变量的时空分布［45-46］。然而由于成本原因，对系统内相关因素进行无限制观测是不现实的。因此，研究观测资料对同化效果的影响是必要的。选择42个水位观测井处的观测水位以及高崖和正义峡水文观测站处的黑河流量观测数据，分别研究观测数为7、14、21、28、35、42 以及44 时对同化效果的影响。图5 显示了经过2 次参数更新过程之后，不同观测资料数的RMSE 值。由于涉及到不同类型的观测值、输出值（地下水位、流量），所以，图中对地下水水位、流量的观测值及输出值进行了归一化处理，将观测值、输出值限定于［0，1］之间。由图5 的总体趋势上可以看出，随着观测资料的增加，参数逐渐接近真实值，地下水位的RMSE 值逐渐降低。然而，观测数从7 个增加至14 个对同化效果影响不明显；观测井数增加至21 个之后，同化效果基本保持不变；增加流量观测（42 至44）对同化效果影响较为显著。由此可见，一种类型的观测数据确实会提升同化效果，但是当一种类型的观测数据增加到一定程度时（本实验中为21 个），观测数据对同化效果的影响有限；然而，继续增加不同类型的观测数据（河流流量观测数据）将进一步提升同化效果。

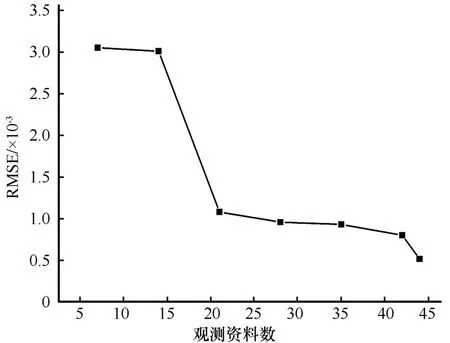
图5 不同的观测数对ESMDA-EnKF算法效果的影响Fig.5 Results of ESMDA-EnKF for different number of observations

3.1.3 集合大小对不确定性分析的影响

EnKF 采用样本集合的方式表示模型状态变量的先验概率分布，估计误差协方差［47］。Hamill 等［48］研究发现，EnKF 中的背景误差协方差估计和滤波函数的最优相关尺度等均与样本集合大小相关；当样本集合比较小时，协方差的估计噪音较大、最优相关尺度较小，出现滤波发散现象，且集合大小直接影响算法运行时间。因此，采用不同的集合大小运行算法，以探索集合大小对算法同化效果的影响。图6 显示了模型参数集合大小分别为30、60、90、120、150 情况下，经过两次参数更新之后的RMSE 值。由图中可以看出，当参数集合大小为30时，并没有出现滤波发散现象，且增加采样对同化效果的影响并不明显。因此，本文将集合大小设置为30以平衡算法效果与计算消耗。

图6 不同集合大小对ESMDA算法效果的影响Fig.6 Results of ESMDA for different ensemble size

3.2 地下水模型参数不确定性分析

基于以上分析确定了算法参数之后，本文利用ESMDA-EnKF 对地下水模型参数进行了不确定性分析，模型参数分布见图7，相关设置见表1。从模型参数先验概率分布中进行30 次随机采样，使用42 个水位观测井、2 个径流观测站处的观测数据对模型参数进行2 次（Na=2）更新。模型参数随ESMDA-EnKF 运行所得的不确定性如图8（注：由于参数与观测点数较多，图8 中只显示了部分参数与观测点处的更新情况）。由图8 可以看出，无论参数的初始分布如何，每次执行ESMDA-EnKF 算法都会对模型参数进行更新，使参数值更接近其标定值。第一次执行算法对模型参数的更新效果显著，大多模型参数在进行第一次更新之后，参数值已经较为接近参数标定值，不确定性明显减小；在进行第二次更新之后，模型参数均分布于标定值附近，模型参数的不确定性进一步减小。图8 第三列显示了各个参数在ESMDA-EnKF 算法执行完成之后的分布情况，由此分布情况可以看出，各个分区的渗透系数（P1～P8）的不确定性显著减小，基本收敛于最优值附近。对比各个分区的渗透系数可以看出，经过ESMDA-EnKF 算法更新之后，第Ⅷ个分区的渗透系数（P8）的分布最分散，不确定性最大，这可能是由于在此分区内观测数据较少，导致算法无法对参数进行有效更新。在算法执行完成之后，黑河子分区Ⅰ与子分区Ⅱ的河床水力传导系数（P9与P10）虽然也收敛到了最优值附近，但是其分布比黑河子分区Ⅲ的河床水力传导系数（P11）分散（即其标准差比较大）。这可能是由于在黑河子分区Ⅰ与子分区Ⅱ河段，黑河与地下水相互作用频繁（子分区Ⅰ河段河流补给地下水，子分区Ⅱ河段地下水出流转化为河流），导致河床水力传导系数不确定性较大。由图8 可见，ESMDA-EnKF 算法能够对模型参数进行有效更新，从而减小模型参数的不确定性。

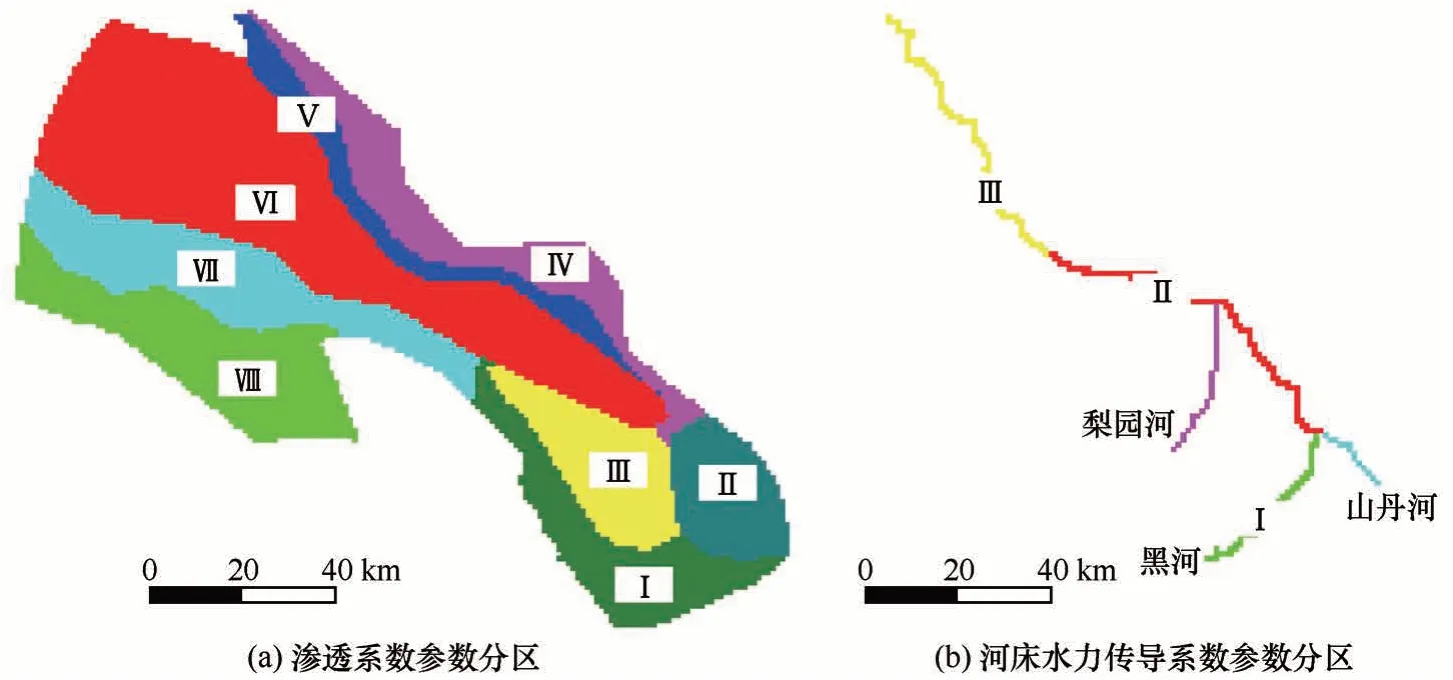
图7 地下水模型参数分区Fig.7 Zonation of the parameters：hydraulic conductivities of the aquifer（a）；hydraulic conductance of the streambed（b）

图8 经过ESMDA-EnKF更新之后的模型参数分布（参数编号解释见表1）Fig.8 Parameter distributions after the updating by ESMDA-EnKF（The numbers of parameters are shown in Table 1）

表1 进行不确定性分析的参数及其设置Table 1 Parameters involved in uncertainty analysis

地下水位随ESMDA-EnKF 运行所得的不确定性如图9 所示。由图9 第一列可以看出，受模型参数不确定性的影响，研究区内地下水位［图9（a）、（b）］以及河流径流量［图9（c）、（d）］均存在较大的不确定性，且随着时间变化，不确定性区间有变大的趋势，这可能是受预报前期模型运行结果不确定性的累积影响，模型运行后期地下水位与河流径流量运行结果产生了更大的不确定性。图9 第二、三列分别为ESMDA-EnKF 算法运行1、2 次之后的模型输出值。可以看出，ESMDA-EnKF算法运行一次之后，模型输出的地下水位与河流径流量的不确定性范围明显缩小，无论是数据起伏较小的地下水位还是数据起伏较大的河流径流量，都收敛到了最优值附近。第二次执行ESMDA-EnKF 算法则基本消除了模型输出结果的不确定性（对应于图9 的第三列）。

图9 使用ESMDA-EnKF对模型参数进行更新之后的模型输出值Fig.9 Model outputs after the update of model parameters by ESMDA-EnKF

对比图8～9 可以看出，随着ESMDA-EnKF 算法的执行，图8中的模型参数逐渐收敛于参数最优值，相应地，通过模型参数计算得到的模型输出也逐渐接近观测值（图9）。由算法对参数的更新可以看出，对观测数据最为敏感的模型参数为第二个参数分区以及第六个参数分区的渗透系数P2 和P6。最不敏感的参数为第八个参数分区的渗透系数，这可能是因为此区域紧邻不透水边界，且区域内没有河流，其与其他区域的水力联系较弱，而在此分区内缺乏有效的观测数据，无法对模型参数进行有效更新。图9显示了在不同算法运行阶段的模型输出值变化，由灰色逐渐加深为黑色，分别为不同迭代次数的模型输出值，由图中可以看出含水层渗透系数（P1～P8）、含水层给水度（P12）以及灌溉回流系数（P13）对模型地下水位影响显著。由图8～9 中河流流量与河床水力传导系数的同化效果可以看出，水力传导系数对河流流量观测较为敏感。河床传导系数会影响河流与地下水之间的水量交换，然而，河流流量还受模型模拟区域内整体地下水水位以及上游来水量的影响，所以，仅使用高崖和正义峡水文站处流量观测值对河床水力传导系数进行更新，无法完全消除其不确定性。

为了定量的分析地下水模型参数的不确定性，同时进一步说明ESMDA-EnKF 算法对地下水模型参数及输出不确定性的更新效果，本文运用Origin 2018 软件对ESMDA-EnKF 第2 次迭代后的地下水模型参数以及第2 次迭代后地下水模型最后时刻（2008年12月）的输出结果（地下水位、河流流量）进行了统计分析。地下水模型参数的统计指标见表2，地下水模型输出结果的统计指标见表3。由表2中可以看出，经过ESMDA-EnKF 算法更新后，地下水模型参数的标准差比更新之前明显变小，且参数均值与表1中参数均值基本相同。虽然更新之后的参数均值与参数的标定值相似，但是仍有细微差别，这可能是由于算法中仅按照相应的分布随机采样了30 个样本，样本数较小导致抽样误差（sampling error）较大，但是根据中心极限定理（central limit theorem）可知，采样之后的均值服从正态分布，因此，均值误差在可接受的范围之内。

表2 ESMDA-EnKF算法第2次迭代后地下水模型参数统计值Table 2 Statistical values of groundwater model parameters after two iterations of ESMDA-EnKF

表3 ESMDA-EnKF算法第2次迭代后地下水模型最后时刻的输出结果Table 3 Statistical values of groundwater model outputs in the last time step after two iterations of ESMDA-EnKF

4 结论

本文提出了基于数据同化的不确定性分析方法，通过包含观测资料信息减小模型参数的不确定性。基于已构建的黑河流域中游地下水模型，利用提出的算法对模型参数进行不确定性分析，探索了不同超参数对算法效果的影响，分析了含水层渗透系数、河床水力传导系数、含水层给水度、灌溉回流系数的不确定性，评估了不同系数对观测信息的敏感程度，主要结论如下：

（1）基于贝叶斯理论的数据同化方法是不确定性分析的有效手段，ESMDA-EnKF算法通过包含观测资料更新参数，能够有效的减小模型参数的不确定性；对不确定性分析结果的统计分析结果表明，经过ESMDA-EnKF 算法更新后的参数均值收敛到最优均值附近，不确定性范围明显减小。

（2）不同超参数对算法效果影响不一，观测资料的增加将提升算法对模型参数的更新程度，减小参数的不确定性，且加入新类型的观测资料会进一步减小参数的不确定性。

（3）不同模型参数的不确定性不同，地表水与地下水相互作用频繁的区域参数不确定性较大；含水层渗透系数、含水层给水度以及灌溉回流系数对模型输出的地下水位影响显著，水力传导系数对模型输出的河流流量影响较大。