一种感光不均匀数字PCR荧光图像分割算法*
2022-02-12余跃,唐骏,肖旻
余 跃,唐 骏,肖 旻
(厦门理工学院 通信工程系,福建 厦门 361024)
0 引 言
数字PCR(Polymerase Chain Reaction)是新一代核酸检测技术,具有高灵敏度、高特异性以及绝对定量的优点,相较于实时荧光定量PCR(Real-time Quantitative PCR,RT-qPCR)不依赖Ct值和标准曲线就可以进行精确的绝对定量检测[1-2]。本世纪以来,基于微纳制造工艺的集成微腔室阵列芯片的数字PCR实现平台在病毒检测、癌症标志物稀有突变检测以及食品病毒学等领域展现出巨大优势与应用前景[3-4],准确地分割数字PCR荧光图像微腔室对提升数字PCR检测精度具有重要意义。然而,在获取数字PCR荧光图像过程中,通常会面临感光不均匀的情况,使得从所采集的图像中分割微腔室的难度增大。由数字PCR技术原理可知,从荧光图像分割出的有效腔室越少,绝对定量准确度越低[5-6]。
当前,在数字PCR荧光图像分割中常用的方法有全局自适应阈值法、局部自适应阈值法以及基于深度学习的分割算法等[7-8]。由于荧光图像存在感光不均匀的现象,全局自适应阈值法和局部自适应阈值法分割准确率较低。文献[9]根据荧光图像直方图的分布特点使用Otsu算法选取双阈值进行分割,但不适用于感光不均匀的荧光图像。为提高分割准确率,文献[10]中在去除光照分量基础上再使用Otsu算法分割,但其分割结果中仍存在大量有效信息丢失。近年来,随着深度学习在图像领域应用的日益广泛,有学者将深度学习技术引入数字PCR荧光图像分割:文献[11]中将Mask R-CNN模型应用于数字PCR荧光图像分割,通过残差运算搭建深层次的网络结构进行实例分割;文献[12]中通过先进行微腔室精确定位再使用微腔室及其周围腔室参数作为随机森林分类器训练集进行训练,实现微腔室分类。然而这些算法主要针对感光均匀图像中阳性腔室的检测,而对感光不均匀区域较大且密集度高的数字PCR荧光图像难以准确检测出目标腔室,会将大量感光不均匀区域的伪阳性腔室错判成阳性腔室。
基于上述问题,本文提出了两步分割算法,实现感光不均匀数字PCR荧光图像的分割。该算法首先利用传统Otsu算法对预处理后的图像进行第一步分割,再使用改进后的Otsu算法进行第二步分割,结合两步分割结果形成最终分割图像,实现感光不均匀数字PCR荧光图像的自动分割。
1 第一步分割算法
首先将待处理图像转化为灰度图像,并进行双线性插值处理提升图像细节表现力[13]。由于图像部分区域偏暗或偏亮,利用自适应直方图均衡化可增强图像清晰度和对比度。为了进一步突出反应腔室的特征,采用Top-hat变换和Bottom-hat变换提高图像对比度。
使用Top-hat变换和Bottom-hat变换分别提取图像灰度峰值和灰度谷值部分:
That(f)=f-(f∘b),
(1)
Bhat(f)=(f·b)-f。
(2)
式(1)和式(2)中:That(f)表示灰度峰值部分,f表示自适应直方图均衡化后的图像,f∘b表示使用结构元素b对f进行开运算;Bhat(f)表示灰度谷值部分,f·b表示使用结构元素b对f进行闭运算。之后对上述结果进行组合运算达到增强图像对比度的效果:
I=That(f)+g-Bhat(f)。
(3)
式中:g表示双线性插值结果,I表示对比度增强后图像。
经过上述处理,图像仍存在噪声,使用中值滤波和高斯滤波可大幅改善图像质量[14]。
Otsu算法依据灰度直方图确定分割阈值[15-16],基本原理如下:设图像灰度级数为L,灰度i出现的概率为h(i),以阈值T将图像分为背景S0(T)=[0,…,T]和前景S1(T)=[T+1,…,L-1],背景与前景的概率分别为
(4)
(5)
则背景与前景的平均灰度值分别为
(6)
(7)
整幅图像的平均灰度值为
μ=G0(T)μ0(T)+G1(T)μ1(T)。
(8)
于是,当阈值为T时,背景与前景的类间方差为
σ2(T)=G0(T)(μ0(T)-μ)2+G1(T)(μ1(T)-μ)2
(9)
将T遍历灰度区间,得到σ2(T)最大时的Thre1为图像最优分割阈值:
(10)
使用Otsu算法进行第一步分割结果如图1所示,可见图中部分区域分割不完全。

图1 第一步分割结果
2 第二步分割算法
因感光不均匀区域干扰,导致第一步分割后的图像存在许多分割不完全区域,且这些区域的面积通常比单个腔室的面积大得多。因此,可以通过连通域面积大小来确定分割不完全区域,对其进行第二步分割,流程如图2所示。

图2 第二步分割流程图
2.1 基于Otsu算法的局部阈值法
局部阈值法将图像划分为若干子区域,再对每个子区域分别计算最优分割阈值,可降低非均匀感光带来的影响。设计基于Otsu算法的局部阈值法对感光不均匀区域进行第二步分割。
首先,统计图像分割不完全区域个数为n,再逐个对分割不完全区域灰度图进行预处理,预处理包括图像增强和图像滤波。然后,使用Otsu算法分割后填补到原位置,待所有区域分割完成后,通过逻辑运算消除图像灰度之间的不连贯,进而形成最终分割图。算法流程如图3所示。该算法可在第一步分割基础上对部分感光不均匀区域进行分割,但算法步骤繁多、复杂度高。
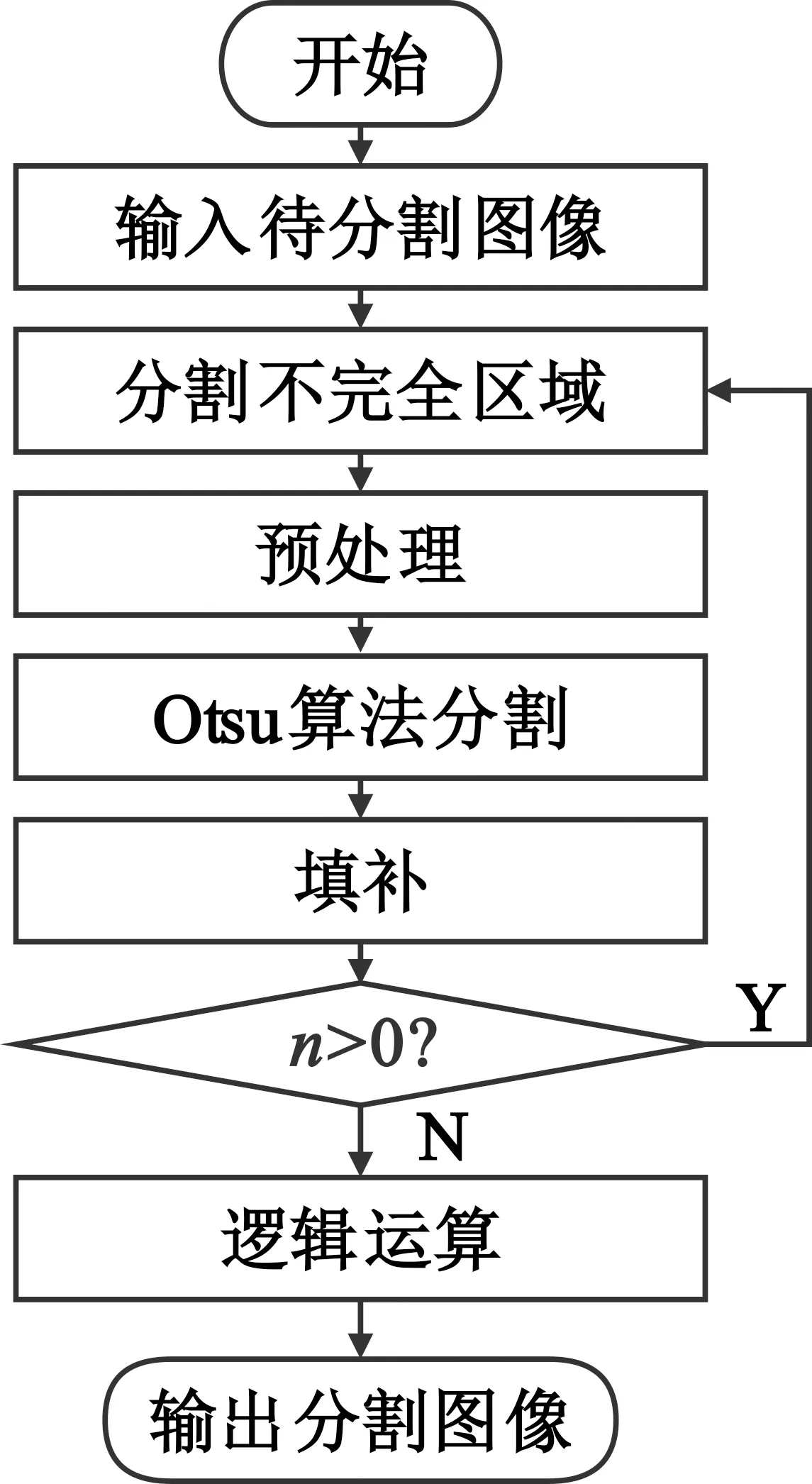
图3 局部阈值法分割流程图
2.2 改进Otsu算法
图像复杂度是用来反映图像内部的复杂程度,可描述图像进行某些处理(如图像增强、图像分割、图像识别等)时内在的困难程度[17]。基于广义集合的图像复杂度的计算公式为
(11)
式中:C表示图像复杂度,单位为b;t表示划分目标区域和背景区域的分割阈值;n(k)表示灰度k的像素个数;N表示图像像素总数。
广义集合中元素具有互异性、无序性以及确定性的特点,可知影响图像复杂度的因素是图像灰度级数量和其出现的频次,而与灰度本身大小无关。图像复杂度是图像的一种客观属性,由其性质可知,图像整体复杂度大于等于各部分复杂度之和[18],故图像灰度级数量与其出现频次的变化会影响图像复杂度大小。由传统Otsu算法原理可知,当图像暗像素过多时会拉低分割阈值,亮像素过多时会拉高分割阈值[19]。因此,在确定分割阈值前,利用图像复杂度的性质确定待分割区域的大致灰度范围,减少较低和较高灰度对分割阈值确定的影响,再基于该灰度范围内灰度统计信息计算最优分割阈值。这样克服了传统Otsu算法需要统计所有灰度信息再计算分割阈值的缺点,阈值的选取会更加快速准确,且分割效果更好。
假设待分割图像f(x,y)总像素数为N0,灰度级数为L,灰度值为k的像素数为n(k),利用公式(11)计算全局图像复杂度为
(12)
图像最小灰度值和最大灰度值分别记做Zmin和Zmax。由于待分割图像为第一步分割不完全区域,待分割区域灰度范围最小值和最大值应位于阈值Thre1两侧,故令初始阈值T0为Thre1。以迭代步长为1的速度同时缩减图像灰度区间两端灰度值,缩减后最小灰度值和最大灰度值分别为α和β。设灰度区间(α,T0)和(T0+1,β)的像素总数分别为N1和N2,则两区间内图像复杂度C1和C2分别为
(13)
(14)
灰度区间(α,T0)和(T0+1,β)内像素总数占灰度区间(α,β)内像素总数的比例分别为r1和r2:
(15)
(16)
则灰度区间(α,β)的平均复杂度为
(17)
假设存在任意大于0的数ε,当最小灰度值为α、最大灰度值为β时满足迭代条件
(18)
α和β的取值范围分别为
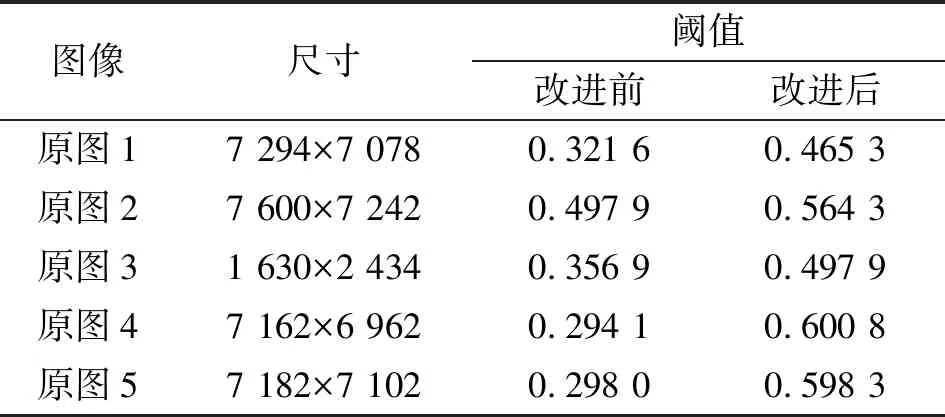
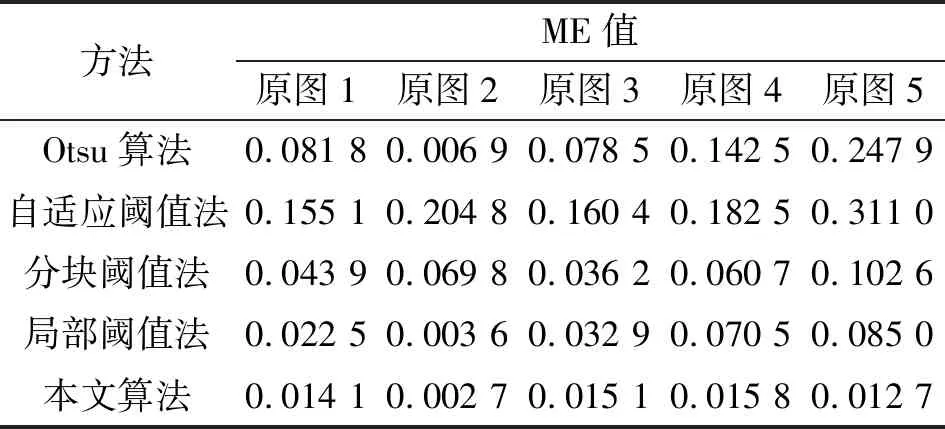
Zmin≤α 式(18)中:ΔC表示灰度缩减前后图像复杂度的变化量;ε用于控制灰度缩减程度,ε越大,表示待分割区域灰度范围越小。ε的数值可根据图像感光不均匀程度确定。经仿真验证,针对数字PCR荧光图像感光不均匀区域的分割,ε取0.5C0时计算的分割阈值更准确。 通过上述算法确定最终待分割区域的灰度范围为(α,β),统计该范围灰度信息,寻找使该范围的类间方差最大的阈值Thre2,再利用Thre2对图像进行分割: (19) 最后通过逻辑运算将第一步分割结果与f*(x,y)合并,形成最终分割图像。 为验证本文算法的有效性,对感光不均匀数字PCR荧光图像进行了仿真实验。实验平台是Intel(R)Core(TM)i5-8265U CPU @ 1.60 GHz,编程环境为Matlab R2020a。图1(a)是一幅数字PCR荧光图像局部,可以看出该图中含有感光不均匀区域。图4(a)描述的是荧光图像第1 360列的第1 220~1 500行灰度在对比度增强前后的波动曲线,分析可知,图像对比度增强后波动曲线的波峰与波谷之间灰度差值增加,达到了图像对比度增强的效果。图4(b)是预处理后的图像,可以看出预处理不仅改善了图像灰度分布的均匀性,而且使腔室特征更加明显。提取第一步分割不完全区域使用局部阈值法进行第二步分割结果如图4(c)所示,该法虽然分割了该图的微腔室,但耗时较长,鲁棒性不好,算法复杂度高。 图4 预处理及局部阈值法分割结果 使用本文改进的Otsu算法进行第二步分割,并选择传统Otsu算法、自适应阈值法以及分块阈值法同时进行对比实验。图5(a)是第一步分割不完全区域灰度图,可以看出该图对比度低且灰度像素分布不均匀。经预处理后使用传统Otsu算法分割结果如图5(b)所示,由于图像低灰度像素过多,严重拉低了分割阈值,导致待分割区域中央丢失了若干目标。图5(c)是自适应阈值法分割结果,待分割区域边缘受到低灰度像素的干扰,几乎分割不出腔室的形状,而在其他区域也存在严重的噪声干扰,腔室之间粘连严重。图5(d)是分块阈值法分割结果,由于分块大小固定,受灰度分布不均匀的影响,分割后的图像不连贯。图5(e)为本文改进的Otsu算法分割结果,该法消除了过高与过低灰度的影响,腔室被准确分割出来,且边缘也未受到低灰度像素的干扰。图5(f)是使用改进的Otsu算法进行第二步分割并与第一步分割结果合并形成的最终分割图,可见本文的两步分割算法有效分割了光照不均匀荧光图像的目标腔室,分割后的图像自然连贯,腔室边缘清晰完整,反映了腔室的实际情况。 图5 第二步分割结果 为进一步验证本文算法的有效性,又对另外四幅感光不均匀荧光图像进行了分割,从图6分割结果看出,传统Otsu算法和自适应阈值法分割结果粘粘严重,无法分割出目标腔室;分块阈值法分割后的图像块与块之间连接不自然,甚至部分区域有效信息丢失;局部阈值法对原图5的分割结果中部分腔室未能准确分割;而本文算法对几幅图像都进行了准确分割,所分割的目标腔室轮廓清晰,包含腔室质心,为荧光信号提取提供了保障,从而也验证了本文算法的有效性。表1为Otsu算法改进前后阈值对比,可以看出改进后Otsu算法分割阈值高于传统Otsu算法分割阈值。由于第二步分割对象主要是感光不均匀区域,其阈值会高于第一步分割阈值,符合待分割图像实际情况。 图6 分割算法实验结果对比图 表1 Otsu算法改进前后阈值对比 为测试改进的Otsu算法分割速度,使用不同算法对五幅图像第二步分割耗时进行比较,各算法耗时如表2所示。由表中数据可知,本文改进的Otsu算法分割耗时低于其他算法,与局部阈值法相比,不仅提升了分割效果,降低了算法复杂度,也提高了算法的运行速度。 表2 五种分割算法耗时对比 为对各算法分割结果进行定量评估,本文选用人工手动分割结果作为标准二值掩码(Ground truth,GT)进行误分类误差(Misclassification Error,ME)计算[20]。ME值可对各算法分割性能进行客观评价,ME值越低表示算法分割性能越好,其数值定义为 (20) 式中:B0和F0表示标准二值掩码中的背景和前景,BT和FT表示分割结果中的背景和前景,|·|表示取集合元素总数。表3给出了几种算法分割结果的ME值,由表中数据分析可知,自适应阈值法分割误差最大,本文所提两步分割算法分割误差最小且分割效果更好。 表3 五种分割算法ME值对比 为了解决感光不均匀数字PCR荧光图像分割准确率低的问题,本文提出了一种两步分割算法。第一步分割使用传统Otsu算法,第二步分割使用改进的Otsu算法。其中,在第二步分割中改进了传统Otsu算法需要统计所有灰度级信息再计算阈值的缺点,通过先确定待分割区域的阈值范围,然后基于该范围的灰度统计信息计算分割阈值,提升了阈值选取的准确性,且分割效果更理想,实现了感光不均匀数字PCR荧光图像的分割。本文算法与局部阈值法、自适应阈值法以及分块阈值法的对比结果表明,本文算法鲁棒性好、复杂度低,可以实现不同程度感光不均匀数字PCR荧光图像的分割,分割结果准确反映了腔室的实际情况。这一研究可用于芯片式数字PCR芯片阅读仪的分析软件中,解决目前数字PCR荧光图像处理速度慢准确率低等问题。本文算法也可拓展应用到其他存在感光不均匀图像的分割中,具有一定的借鉴意义。但从整体算法流程可知,本文算法需经两步分割完成整幅图像的分割,接下来将继续对图像进行算法研究,进一步简化分割算法流程。3 实验结果与分析




4 结束语
