高可靠性信道反馈自编码器系统设计*

袁治中，王旭东，吴 楠

(大连海事大学 信息科学技术学院，辽宁 大连 116026)

0 引 言

在过去的十几年里，深度学习在计算机视觉和语音处理领域取得了巨大的成功。近年来，越来越多的学者开始在无线通信领域中应用深度学习技术，其应用方式主要分为两种：一种是将通信系统的某个独立的模块用深度学习的方法代替，如信道解码[1,2]、信道估计[3]、信道检测[4]、调制分类[5]等；另一种是将多个独立的模块联合进行训练，寻求整体上的最优方案，以提升系统的性能，例如可以利用自编码器(Autoencoder,AE)学习框架，构建一个端到端的通信系统，在信道编码[6-9]、正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)及多输入多输出(Multiple-Input Multiple-Output,MIMO)系统设计[10-11]中均有其典型应用方案。

纠错编码引入信息比特的冗余来消除信道噪声和其他信道失真的影响，是实现可靠通信的关键技术之一。尽管各种编码方案已经被各种通信系统所采用，但是针对许多具有实际意义的系统结构仍然缺乏有效可靠的编码方案，其中带有输出反馈的信道编码就是一个长期存在的问题。香农曾指出，信道反馈不会增加无记忆离散信道的信道容量，但可以提高信道编码的可靠性[12]。由于传统的编码方案并不适用于信道反馈编码，一些学者提出了相应的解决方案，验证了信道反馈可以提高系统的可靠性，但是在反馈信道有噪声时编码方案无法充分利用反馈信息[13-15]。针对这一问题，文献[16]提出了基于深度学习技术，通过神经网络来利用反馈信息学习信道反馈编码的思想。

根据反馈信息的不同可以分为主动反馈和被动反馈，直接将接收端接收到的信息反馈到发送端称为被动反馈，将接收到的信息进行编码再反馈给发送端称为主动反馈。文献[16]主要讨论的是单位延迟反馈，实际的反馈通常被延迟一段随机的时间，因此文中还提出了一种多位延迟反馈。在文献[16]的基础上，本文提出了一种针对带有反馈信道的高可靠性自编码器系统设计方案(Feedback Channel Autoencoder,FBC-AE)，它是基于块延迟的被动反馈模型。与文献[16]不同，FBC-AE系统在发送端引入反馈解码器模块，发送端接收到反馈信息之后，先经过反馈解码器模块对反馈信息进行提取处理，再传入编码器模块进行编码。本方案把对反馈信息的提取以及编码分成了两部分，由两个模块分别进行处理，从而降低了编码器训练难度，同时提高了反馈信息的利用率。

本文的主要贡献如下：

(1)FBC-AE系统引入反馈解码器模块，适用于不同码速和不同反馈信道信噪比，系统误码性能优于目前文献[16]给出的方案。

(2)基于FBC-AE系统，提出的部分反馈方案可以在反馈信道环境较差时节省反馈发送功率和提升系统的误码性能，通过控制抽样间隔可以灵活控制反馈发送功率。

1 系统模型

1.1 FBC-AE系统模型

FBC-AE系统框图如图1所示，整个通信系统模型包括发送端、信道和接收端三部分。其中发送端包括编码器和反馈解码器，信道包括正向信道和反馈信道，接收端包括解码器。

图1 FBC-AE系统框图

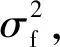
在全连接神经网络或卷积神经网络(Convolutional Neural Network,CNN)中，每层神经元的信号只能向下一层传播，样本的处理在各个时刻独立，而循环神经网络(Recurrent Neural Network,RNN)中，神经元的输出可以在下一个时间段直接作用到自身。门控循环单元(Gated Recurrent Unit,GRU)在RNN的基础上增加了更新门和重置门，实现了长期记忆的功能。

FBC-AE系统一共有3个编码器，均由两层GRU和一层全连接层组成，它们分别工作在第1、3、5三个时间片内。编码器的主要作用是在发送端完成编码任务，在第1个时间片内，没有反馈信息存在，编码器的输入信息是未编码的二进制消息序列x，它的维度为(B,K,1)，其中B为最小批处理量(Mini-Batch)的大小，K和1表示块长度为K的二进制消息序列x=(x1,x2,…,xK)。在第3、5时间片内，存在反馈信息，未编码的二进制消息序列x和经过反馈解码器处理过的反馈信息u在最后一个维度上连接一起，得到编码器的输入信息[x,u]，其维度为(B,K,2)。编码器的输入信息先经过两层的GRU，利用反馈信息将输入映射到高维空间。本文所讨论的编码块长度为50，考虑复杂度以及训练难度对系统的影响，选择将编码输入映射到100维空间，通过一个全连接层完成特征空间维度的转换，得到所需的维度大小。表1列出了编码器的网络参数。

表1 编码器网络参数

解码器需要在接收端恢复被噪声破坏的编码信息，处理的任务相对复杂，因此采用双向门控循环单元(Bi-directional Gated Recurrent Unit,Bi-GRU)。Bi-GRU由两个单向GRU折叠在一起，两个单向GRU神经元之间的传递方向相反，因此每个时刻的输出不仅与之前的信息有关，还与之后的信息有关，在进行解码时，每个比特位的解码都跟前后比特位相关，提高解码的准确性。

如图1所示，在第1、2时间片内，编码信息y1经过正向信道和反向信道后，发送端接收到反馈信息w2，其表达式为

w2=P(P(y1)+n)+nf。

(1)

式中：n和nf分别表示正向信道噪声和反向信道噪声；P表示功率归一化，

(2)

式中：xmean表示x的均值，xstd表示x的标准差。文献[16]在发送端将接收到的反馈信息传入编码器进行编码，编码器利用反馈信息中携带的信道信息提高编码的可靠性。在此基础上，本文将反馈信息提取和编码两部分工作进行细化，提出了反馈解码器模块，发送端接收到的反馈信息w和上一个阶段的编码序列y同时进入到反馈解码器模块，得到输入信息[y,w]的维度为(B,K,2)，反馈解码器把提取出来的信道信息u传入到编码器参与编码。

之所以说是“菜市场”，是因为老师发布一个通知或者信息，群里的家长就会七嘴八舌一通刷屏。再或者，有的家长转条广告链接，班级群成了大卖场。更有甚者，还将自己孩子在学校的学习情况、生活情况、个人问题发到群里，在群里吵翻天，最后不欢而散。

本文提出了两种反馈解码器模型：第一种反馈解码器模型基于CNN，详细参数如表3所示，其中CNN的卷积核大小设置为3，步长设置为1；第二种反馈解码器模型基于Bi-GRU，详细参数如表4所示。两种解码器在不同码速和不同反馈信道信噪比下的性能有所不同，基于CNN反馈解码器的网络参数要少于基于Bi-GRU反馈解码器的网络参数。

表3 第一种反馈解码器网络参数

表4 第二种反馈解码器网络参数

1.2 部分反馈

实验表明反馈信道传输特性较差时，反馈信息会受到反馈信道的严重破坏，因此反馈信息带来的收益较小[15]，同时考虑到节省反馈发送功率，本文提出了一种部分反馈方案，该方案将反馈的K比特信息序列z=(z1,z2,…,zK)等间隔抽样，再在发送端对反馈信息进行补零操作，便于进入到反馈解码器中。由于并没有对反馈信息进行编码操作，因此该方案属于被动反馈模型。

以反馈一半信息为例，经过等间隔抽样得到K/2比特信息序列z=(z1,z3,…,zK-1)，通过功率归一化反馈到发送端，发送端将接收到的反馈信息进行补零操作，得到反馈信息序列w=(w1,0,w3,…,wK-1,0)，经过反馈解码器对反馈信息进行恢复和提取。在接收端，反馈信息减少一半，经过功率归一化后的反馈发送功率也节省了一半，因此该方案可以节省反馈发送功率。该方案可以根据抽样间隔大小灵活控制反馈发送功率，从而达到灵活节省功率的目的。

1.3 训练方法

FBC-AE系统的训练数据由randint函数和reshape函数产生和处理。首先通过randint函数产生维度大小为(M×K,1)的0、1序列，然后使用reshape函数使序列维度变换为(M,K,1)，其维度含义表示为M个二进制消息序列x，每个x的块长度大小为K。本文使用均方误差(Mean Square Error,MSE)作为训练损失函数，其表达式为

(3)

(4)

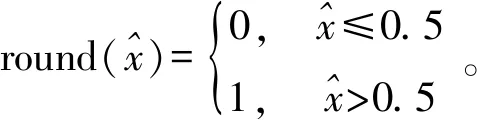
(5)

式(4)中：U为进入神经网络的总比特数，round表示硬判决。优化器采用Adam，它为不同的参数计算不同的自适应学习率，提高系统的收敛能力。将发送端和接收端分成两部分进行训练，即编码器和反馈解码器同时训练，接收端的解码器权重不更新，当接收端的解码器开始训练时，发送端的编码器和反馈解码器权重不更新。在进行端到端训练时，由于本文系统分为多个模块，寻求全局最优解十分困难。当固定一部分模块的权重，寻找未固定权重模块的最优解，可以降低学习难度，提升系统的收敛速度。故在每一次迭代训练中，发送端部分先训练三次，接收端部分再训练三次。

2 性能分析

表5 系统仿真参数

2.1 码速1/3时FBC-AE系统在反馈信道无噪声时BER性能分析

如图2所示，AE without Feedback表示该系统按照图1系统框图构建，删除第2时间片与第4时间片，将编码分为三个阶段，同时删除反馈信道。该条曲线与另外三条曲线对比说明增加信道反馈提高了系统的BER性能。本文所提出的两种不同的反馈解码器在反馈信道无噪声时所表现的性能基本一致，使用CNN反馈解码器的FBC-AE系统在0 dB之后性能优于文献[16]中的结果，在10-7量级，误码性能提升了0.5 dB。

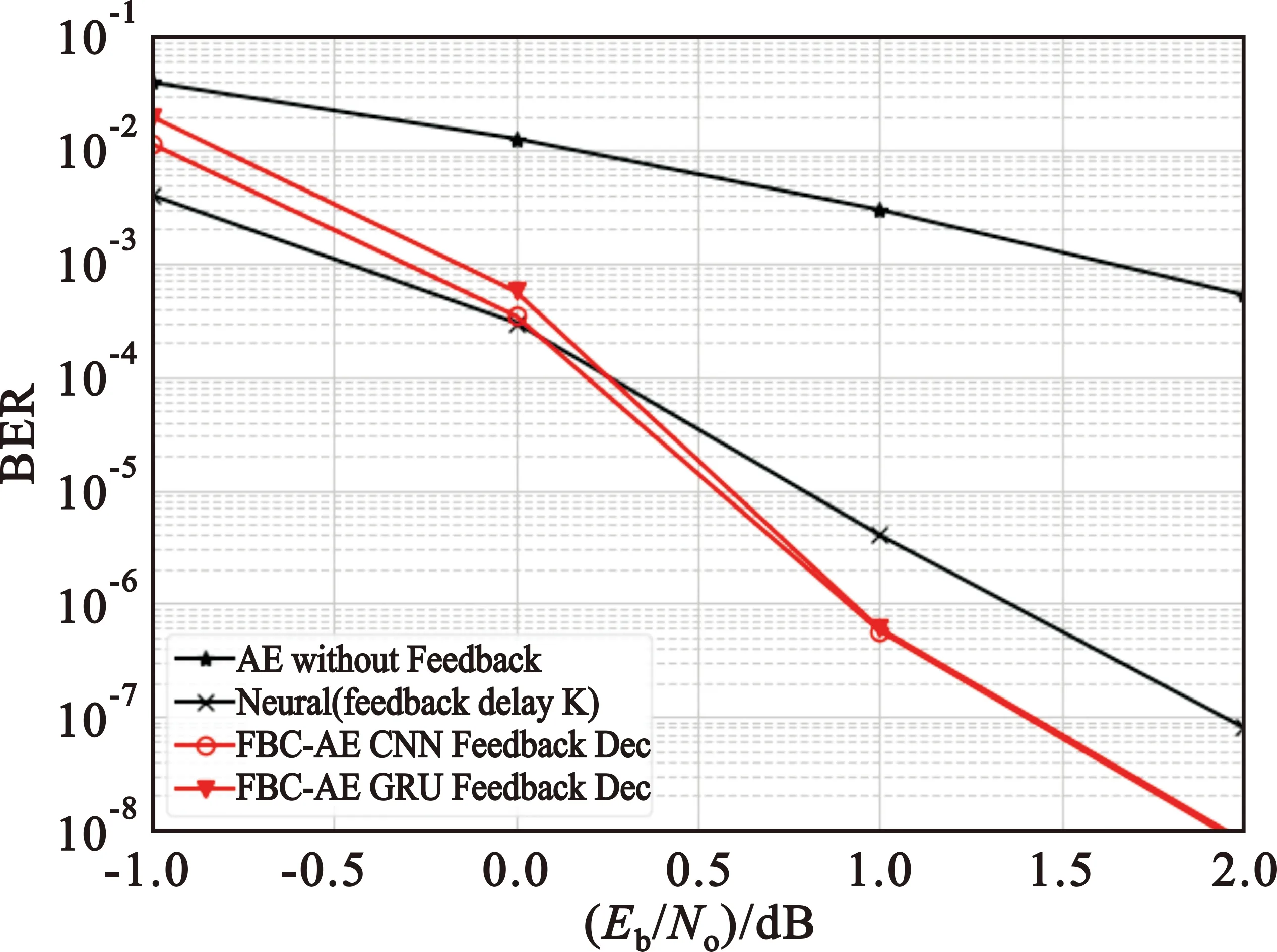
图2 码速1/3时反馈信道无噪声误码性能比较

2.2 码速1/3时FBC-AE系统在反馈信道有噪声时BER性能分析

图3给出了反馈信道信噪比为10 dB和0 dB时的BER曲线。可以看出，当反馈信道信噪比为10 dB时，随着正向信道信噪比的增加，反馈解码器对系统性能的提升越大，在10-3量级，基于CNN反馈解码器的FBC-AE系统误码性能提升了0.65 dB，基于Bi-GRU反馈解码器的FBC-AE系统误码性能提升了1 dB，两种反馈解码器系统误码性能差了0.35 dB。当反馈信道信噪比为0 dB时，在10-3量级，基于CNN反馈解码器的FBC-AE系统误码性能提升了0.3 dB，基于Bi-GRU反馈解码器的FBC-AE系统误码性能提升了0.5 dB。由于反馈信道环境变差，相比于反馈信道信噪比为10 dB时，两种反馈解码器之间的性能差距减少到0.2 dB。

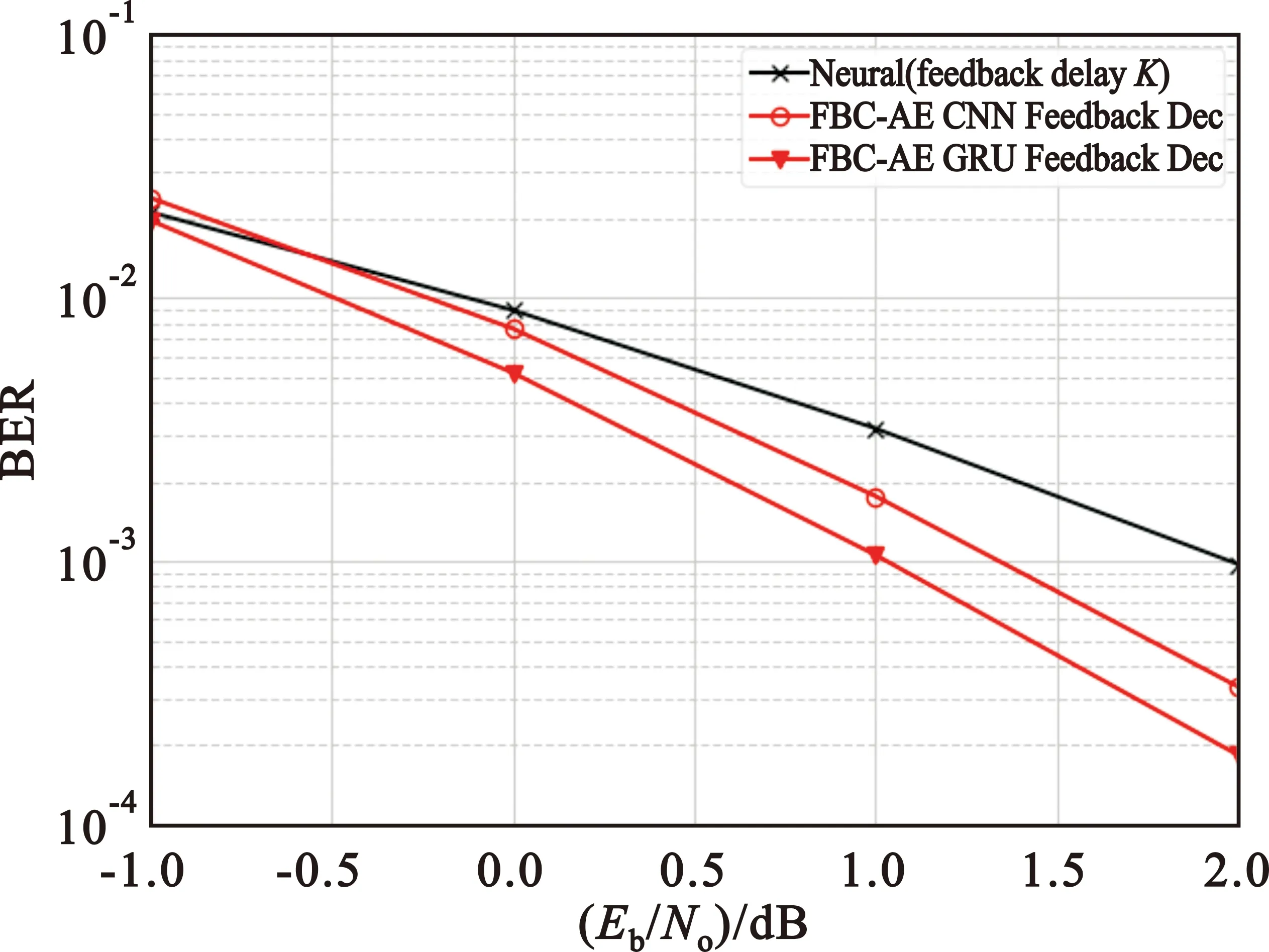
(a)SNR=10 dB

2.3 码速1/2时FBC-AE系统BER性能分析

通过修改图1的系统结构，只保留前三个时间片，此时码速修改为1/2，同时修改文献[16]中结构并与之对比，图4为不同反馈信道环境下的BER曲线。在反馈信道无噪声时，FBC-AE系统性能提升不明显，基于CNN反馈解码器的FBC-AE性能反而没有提升。这是由于改变码速之后减少了反馈的次数，也减少了反馈解码器的个数，同时反馈信道无噪声，相较于1/3码速时解码器的作用减少。在反馈信噪比为10 dB时，FBC-AE系统性能提升较大，在10-4量级，基于CNN反馈解码器的FBC-AE系统误码性能提升了1.48 dB，基于GRU反馈解码器的FBC-AE系统误码性能提升了1.8 dB。在反馈信噪比为0 dB时，两种反馈解码器系统在10-4量级时的误码性能均提升了1.36 dB，这仍是由于反馈解码器个数的减少所导致的。

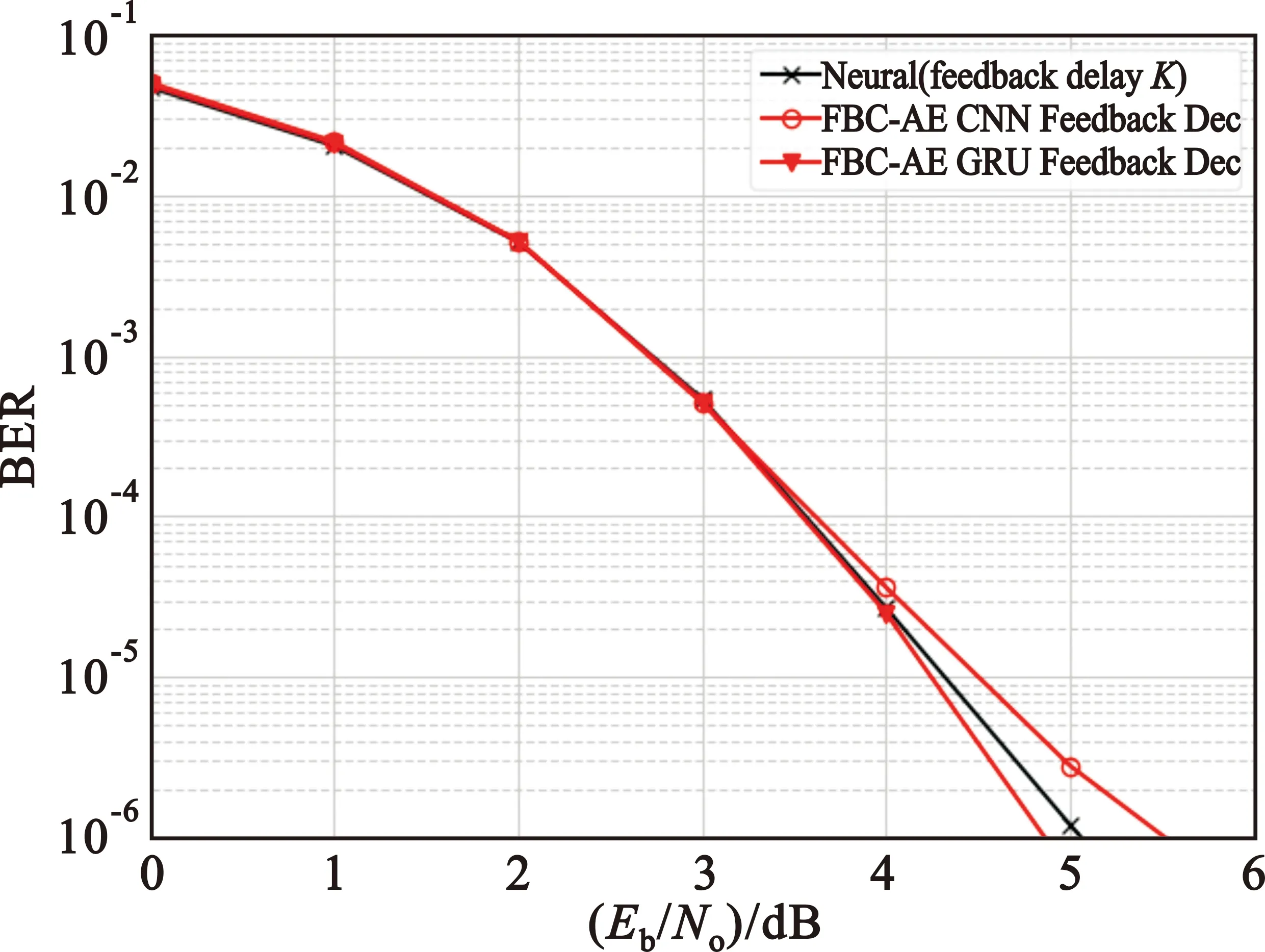
(a)无噪声

2.4 部分反馈方案分析

本实验对部分反馈方案性能进行分析，以反馈一半信息为例，从图5中可以看出，在反馈信道信噪比为0 dB时，反馈信息减少，系统性能不如全反馈时的BER曲线(图3(b))，但是由于反馈解码器的存在，在接收到不完整的反馈信息时，反馈解码器对反馈信息有一定的恢复和提取作用，在10-3量级时的误码性能仍提升了0.1 dB。

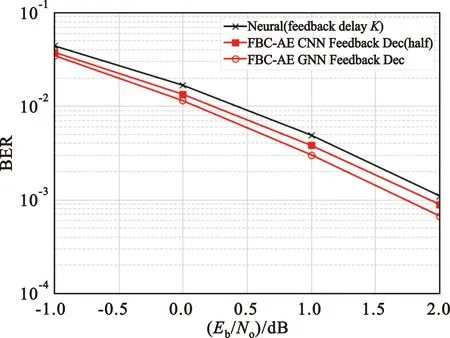
图5 部分反馈误码性能

2.5 系统复杂度分析

为了进一步验证反馈解码器对FBC-AE系统性能的提升，考虑系统参数对结果的影响，将基于CNN反馈解码器的FBC-AE系统的编码器和解码器进行简化，具体简化后的参数如表6和表7所示，不同系统的网络训练参数如表8所示。从图6中可以看出，经过简化后的FBC-AE模型误码性能提升了0.2 dB，说明反馈解码器模块对信道反馈编码系统的误码性能有一定的提升作用。简化后的FBC-AE系统在确保误码性能不损失的基础上，其训练运算复杂度明显降低。

表6 简化后编码器网络参数

表7 简化后解码器网络参数

表8 网络训练参数

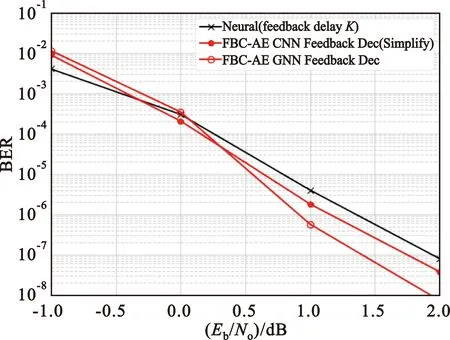
图6 码速1/3时FBC-AE简化模型误码性能

3 结 论

本文提出了一种针对带有反馈信道的高可靠性自编码器系统设计方案，在方案中增加了反馈解码器模块，把对反馈信息的利用以及编码分成了两部分，由两个模块分别进行处理，反馈解码器的主要作用是对反馈信息的提取，然后再把提取后的反馈信息传入编码器，提高了反馈信息的利用，有效提高信道反馈编码系统的可靠性。在不同反馈信道环境、不同码速时，反馈解码器均对系统的误码性能有一定的提升。同时，提出了一种部分反馈方案，通过控制抽样间隔大小可以灵活调整反馈发送功率，从而达到节省反馈发送功率的目的。在反馈信道环境较差时，反馈解码器对部分反馈信息有一定的恢复作用，以反馈一半信息为例，该方案在节省一半反馈发送功率的同时对系统误码性能提升了0.1 dB。此外，本文考虑复杂度对系统的影响，经过简化后的系统模型误码性能提升了0.2 dB，说明FBC-AE系统能有效利用反馈信息，提高系统的误码性能。