一种适用多种空时编码方案的MIMO自编码器通信系统*

2022-02-12王旭东许志远

电讯技术 2022年1期

夏杉，王旭东，吴楠，许志远

(1.大连海事大学信息科学技术学院，辽宁大连 116026；2.大连海洋大学航海与船舶工程学院，辽宁大连 116023)

0 引言

随着无线通信技术的快速发展，频谱资源的严重不足已经成为遏制通信事业发展的瓶颈。如何充分有效地利用频谱资源，是当前通信研究的热点话题。多输入多输出(Multiple-Input Multiple-Output,MIMO)技术自提出以来为无线通信技术的发展提供了更加灵活的应用空间，能在不使用附加发射功率和频谱资源的条件下提升系统的信道容量和频谱利用率。与此同时，深度学习技术作为人工智能领域的科技前沿，逐渐成为研究热潮[1]。随着深度学习技术在图像处理、语音识别等领域取得的巨大突破，其在无线通信领域的应用开始变得活跃。

近年来，深度学习技术在信道估计[2-4]、信号检测[5]、信道信息反馈[6-7]、信道译码[8-10]、调制识别[11]等方面取得了一定的研究进展。其中，深度学习技术用于物理层实现的方式主要分为两类。一种是将通信系统的某一模块单独优化设计，例如，文献[2-3]使用残差学习的思想实现了信道估计算法，并将噪声方差引入到系统中以提升系统的估计精度[3]；文献[4]设计了一种基于全连接(Full Connected,FC)神经网络的信道估计方案；文献[5]提出了一种简单FC网络构成的MIMO信号检测框架。另一种情况是将整个通信系统的所有模块视为一个整体，利用端到端自编码器来实现整个通信系统的设计，通过整体联合优化训练的方式使得系统的性能达到最优。因此有学者提出了基于深度学习自编码器的物理层方案，并开创性地利用FC网络实现MIMO系统设计[12]，虽然在高信噪比时其误码性能优于传统方案，但低信噪比下性能较差，系统泛化能力需要进一步提高。文献[13]为了提升系统泛化能力，利用全连接网络实现了两发一收的空时分组码(Space-Time Block Coding,STBC)方案，然而FC层需要大量的神经网络参数，在构建深度神经网络时会产生梯度消失的问题。文献[14]为进一步提升系统的泛化能力以及系统的可靠性，利用卷积神经网络(Convolutional Neural Network,CNN)实现两发一收的STBC方案，并且在瑞利衰落信道下实现了近似卷积编码的性能改善。

由于上述文献中仅利用深度学习技术实现了满足Alamouti编码方案的MIMO-STBC系统，对于其他的空时分组编码方案[15]以及无编码的垂直分层空时码(Vertically Layered Space-Time codes,VLST)方案并没有完全实现。因此，本文提出一种适用于多种空时编码方案的MIMO自编码器通信系统(AE-MIMO)，利用多个一维卷积层实现信号调制、信号检测、信号解调等子模块；通过端到端的训练方式，联合优化所有模块，使系统性能达到最优；并且利用CNN网络局部连接以及权重共享的特性，传输更多比特信息，增强网络的泛化能力。另一方面，为了使系统得到更高精度的信道估计结果来恢复发送信号，通常使用基于导频的信道估计算法，如最小二乘(Least Square,LS)算法和最小均方误差(Minimum Mean Square Error,MMSE)算法。为了进一步提升信道估计的准确性，本文提出一种基于密集连接卷积网络的信道估计(CNN-CE)方法。通过密集连接卷积网络跨层连接、特征复用的特性，利用多个数据帧内信道间的相关性进行信道估计。这两部分都可以在特定信噪比(Signal-to-Noise Ratio,SNR)下训练并保存权重，同时其训练的结果可泛化到任意SNR下工作。

1 系统模型

本节主要介绍AE-MIMO系统的设计和训练方法，其系统模型如图1所示。本文通过设计一个由发射机、信道和接收机三部分组成的MIMO自编码器通信系统，包含比特信息的符号经过发送端和信道传输给接收机，再通过接收机中的信号检测模块进行信道均衡处理，最终在接收端对受到噪声污染的信息数据进行估计，使其与信源信息尽可能地接近。同时，为了更好地解决信道失真问题，提出了一种基于密集连接卷积网络的信道估计法。在AE-MIMO系统中加入信道估计模块，从而补偿信道失真对系统性能造成的影响，改善系统的误码性能。

图1 AE-MIMO系统结构模型

1.1 AE-MIMO系统模型

考虑发射天线数为Nt，接收天线数为Nr，且M=2k进制符号调制映射的MIMO无线通信系统结构。发送端将输入的比特信息流按照每kNt比特分组转换为独热编码(one-hot)向量S，并将转换后的信源信息S发送到AE-MIMO系统发射机。首先，通过一维卷积层(Conv1D)实现对信源信息S的特征提取，这层Conv1D由128个滤波器构成，将one-hot向量从2kNt维空间映射到128维空间，从高维空间中提取信源信息的更多潜在特征。然后，通过一层Conv1D将高维空间特征映射为两个实数表示的复信号，完成对信源信息的信号调制和空时编码。最后，利用能量归一化层对发射机信号进行能量约束，得到发送信号X。

在无线信道中，传输的信号主要受到信道的乘性干扰与高斯白噪声的加性干扰。系统的信道建模为

Y=HX+N,Y∈Nr×t。

(1)

式中：X和Y分别代表收发机的发送和接收信号矢量；t为空时编码的传输时隙数；N为噪声矢量，其元素满足零均值和单位方差的标准正态分布；H为Nr×Nt维的信道矩阵。

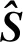
表1、表2和表3分别给出了AE-MIMO系统的发送端结构、信号检测模块结构以及信号解调模块结构。

表1 AE-MIMO发送端结构

表2 AE-MIMO信号检测模块结构

表3 AE-MIMO信号解调模块结构

1.2 信道估计

为了解决信道失真问题并提升信道估计的准确性，本文提出了一种基于密集连接卷积网络的信道估计方法。首先，采用最小二乘方法获取Ns个数据帧内导频位置处的信道信息，通过密集连接卷积网络将Ns个数据帧内的导频信息进行联合估计，利用密集连接卷积网络跨层连接和特征复用的特性获取数据帧间信道信息的相关性，提升信道估计的准确性。尽管Conv1D层数越多神经网络的表示和特征提取能力越强，但随着网络层数的增加会导致网络训练不易收敛。同时，Conv1D层数过少也会导致网络无法达到最优的训练效果。因此，本文选用6层Conv1D所组成的密集连接卷积网络进行信道估计模块的设计。为了实现神经网络跨层连接，本文在每两层Conv1D之间设置了连接层(Concat)。Concat将两个Conv1D的输出按照最后一维进行拼接。信道估计模块的结构参数如表4所示，其中，Concat输出维度[·,·]表示两个数据的拼接。

表4 CNN-CE模块结构

1.3 模型训练

由于AE-MIMO系统与CNN-CE模块所使用的损失函数并不统一，为了使神经网络更容易收敛，本文先将两部分分开训练，再将保存好参数权重的CNN-CE模块加载到AE-MIMO系统中进行整体训练。

首先，AE-MIMO系统将随机生成的二进制数据按照比特映射的方式转换为one-hot向量，并将其作为训练数据和标签数据，在接收端提供完美的信道信息进行信道均衡处理。由于设置的标签数据为one-hot向量，因此可以将整个训练过程视为一种多分类问题。可以利用多分类交叉熵(Cross-Entropy)函数作为损失函数来衡量最终估计结果的好坏，其表达式为

(2)

同样地，CNN-CE将导频信号作为训练数据，完美的信道信息作为标签数据，其损失函数选用均方误差(Mean Square Error,MSE)函数，表达式为

(3)

发送端与信号解调模块的神经网络主要起到信号调制、空时编码与信号解调的功能。当滤波器个数过少时，由于没有足够的高维空间来获取信源信息的潜在特性，导致训练效果较差。同时，滤波器个数过多时会导致训练时间较长，系统不易收敛。因此，本文发送端与信号解调模块滤波器设置为128个，并且在实现低阶调制时可以适当减少滤波器个数。在信号检测模块中，神经网络需要实现非线性信号检测的功能，若设置的滤波器个数过少，会使网络无法收敛至最优点，信号检测性能差。而滤波器个数过多会导致训练时间过长，系统不易收敛。因此，选用256个滤波器进行信号检测模块的设计。

在激活函数上，AE-MIMO系统选用Elu、Linear和Softmax函数来帮助神经网络实现非线性映射、线性映射和分类软判决的能力，CNN-CE模块选用Tanh、Linear函数作为隐藏层和输出层的激活函数帮助神经网络提升信道估计的准确性。同时，为了在训练过程中加快梯度下降的步长与方向，使神经网络更容易收敛，避免精度波动问题，选用自适应矩估计(Adaptive Moment Estimation,ADAM)算法来优化反向传播过程。

此外，训练信噪比的选取是影响系统性能的重要因素[8]。由于神经网络需要在决策边缘接收足够多的训练样本来学习受到噪声污染的信号特征，当信噪比过低时，有用信号会淹没在噪声中，导致神经网络无法提取信号特征，只能学到噪声特征，而信噪比过高时，训练样本受到噪声干扰较小，样本中只有少部分在决策边缘附近，导致系统无法达到最佳的译码性能。因此AE-MIMO系统需要选取适宜的信噪比，保证绝大多数的样本在决策边缘附近，使系统可以学习受到噪声污染的信号特征，并达到最优的译码性能。

本文的数据样本集为随机产生的二进制比特序列，其中，训练集和测试集样本数分别为1 024 000和5 120 000。同时，本文主要在加性高斯白噪声信道、瑞利衰落信道以及突发噪声信道模型中，讨论所提出的AE-MIMO系统与传统无线MIMO系统间的性能差异。

2 性能分析

本节分别训练上面介绍的AE-MIMO系统和CNN-CE模块，选取比特能量信噪比Eb/No在0～25 dB范围内分析系统的误块性能，并与现有的传统无线MIMO系统性能进行比较，在图示中以Expert表示传统无线MIMO系统性能，通过仿真实验证明所提出的系统在不同信道环境、调制方式和编码方式下表现出的性能优势。本文设计的AE-MIMO系统和CNN-CE模块均由基于TensorFlow后端的Keras框架实现，其中，以长期演进的扩展典型城市信道模型(Long Term Evolution Extended Typical Urban model,LTE-ETU)作为瑞利衰落信道的仿真环境[16]，详细系统参数如表5所示。同时，文中仅在实验4与实验5中采用信道估计算法，其余实验中均考虑接收端进行理想信道均衡处理。

表5 系统仿真参数

实验1 在不同信道环境下训练两发一收的AE-MIMO系统，并与传统的STBC(Alamouti编码)系统进行误块率对比。

如图2所示，在加性高斯白噪声(Addition White Gaussian Noise,AWGN)信道下，AE-MIMO系统采用BPSK和QPSK调制时其误块率与STBC编码理论值吻合。在8-QAM和16-QAM调制下，AE-MIMO系统分别在9 dB、10 dB下训练，误块率比Alamouti编码理论值低，在误块率为10-3时分别优于传统系统1.2 dB和0.5 dB。这是因为AE-MIMO系统在进行信号调制和空时编码时，会根据高维空间内获取到的信源信息潜在特性，实现适合当前信道环境的信号映射方式，所以获得了比传统方法更好的误码性能。

图2 AWGN信道下两发一收系统性能比较

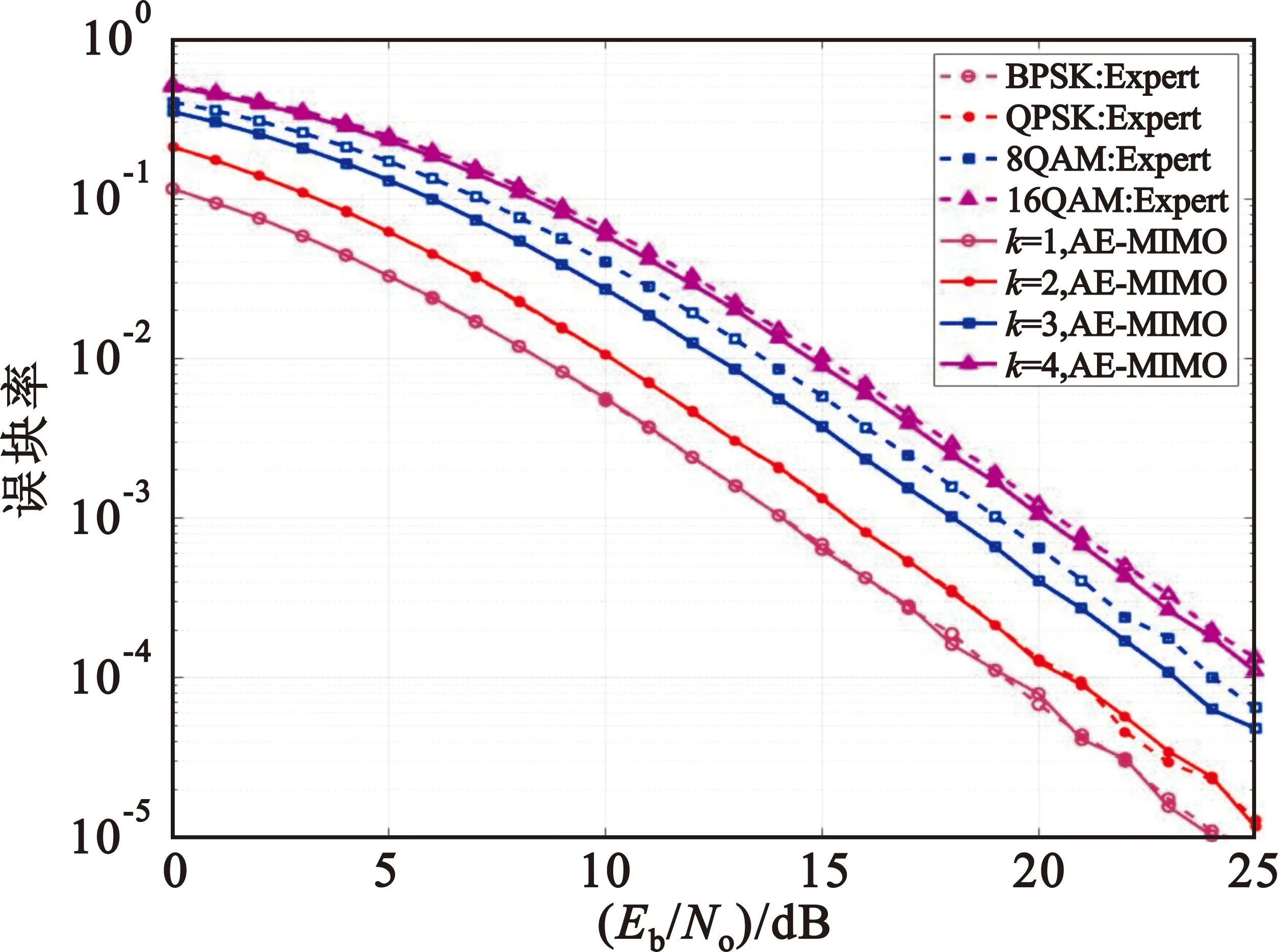
图3 瑞利衰落信道下两发一收系统性能比较

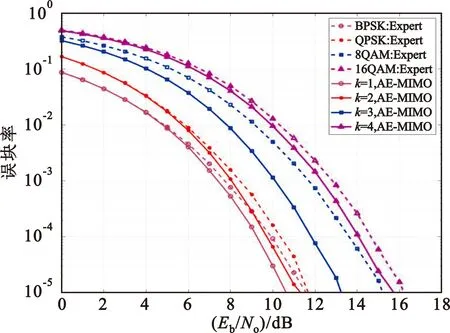
图4 突发信道下两发一收系统性能比较

n1=n+b·nb。

(4)

式中：n为加性高斯白噪声；nb为突发噪声；b为伯努利过程，满足出现概率为ρ=0.05的二项分布。

为了验证AE-MIMO系统在瑞利衰落信道下的系统性能，使用LTE-ETU模型进行信道建模，且接收端具备理想信道状态信息。在BPSK和QPSK调制下，分别在8 dB和10 dB下训练，其误块率与Alamouti编码的理论值相吻合。在误块率为10-3时，AE-MIMO系统在8-QAM和16-QAM调制下可提供优于传统方法1 dB和0.2 dB的性能提升。同时突发信道下，AE-MIMO系统在中高信噪比下均展现出优于传统MIMO系统的误码性能。进一步验证AE-MIMO系统对于不同信道环境良好的适应能力，并且在高阶QAM调制下可以生成一种较传统方法更优的信号映射方式。

实验2 采用两发两收系统，在瑞利衰落信道下比较不同传输时隙数的AE-MIMO系统误码性能。

为了验证系统可以适用于多种空时编码方案，考虑每组传输k个QPSK调制信号，并在瑞利衰落信道下通过改变传输时隙t来匹配不同空时编码方案。其中，码速R=k/t。如图5所示，当t为1时，AE-MIMO系统所生成的编码方案与VLST方案相匹配;t为2、3、4时，AE-MIMO系统与全速率、2/3 码速和1/2 码速的空时分组编码方案所对应。仿真实验表明，增加传输的时隙个数可以提升系统的误码性能，同时所提出的AE-MIMO系统可以通过改变传输的时隙个数来匹配不同的空时编码方案。

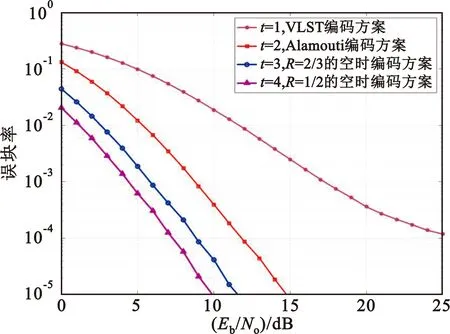
图5 瑞利信道下不同传输时隙两发两收系统性能比较

实验3 对两发两收系统，在瑞利衰落信道下采用QPSK调制以及VLST编码方案训练AE-MIMO系统，并与不同的MIMO信号检测算法进行误码性能和复杂度对比。

为了验证AE-MIMO系统的信号检测性能，采用两发两收的AE-MIMO系统与不同信号检测算法下VLST方案的误码性能进行对比，采用理想信道信息进行信道均衡处理。如图6所示，在QPSK调制下，两发两收的AE-MIMO系统在低信噪比下与传统的最大似然检测(Maximum Likelihood,ML)方法误码率曲线相吻合，在高信噪比下系统的性能仍优于最小均方误差串行干扰消除(Minimum Mean Square Error Successive Interference Cancellation,MMSE-SIC)检测法。在误码率为10-3时，AE-MIMO系统的误码性能优于MMSE-SIC方法3 dB。为了验证信号检测模块对AE-MIMO系统性能的提升，考虑系统参数对性能的影响，将信号检测模块采用2层Conv1D结构，具体简化后的系统参数如表6所示。由于考虑到信号检测技术，简化后的AE-MIMO-S系统在整个测试信噪比下误码性能均优于文献[14]系统，说明信号检测模块对MIMO自编码器系统的误码性能有一定的提升作用。进一步观察，相比于使用文献[5]信号检测方案的AE-MIMO系统，本文提出的信号检测方案在中高信噪比下的误码性能大幅度改善，且神经网络参数量略低于基于全连接网络设计的信号检测方案[5]。这意味着，卷积神经网络通过权重共享和局部连接的方式降低了模型复杂度，同时可以比全连接网络更好地利用信道信息进行信号检测。虽然本文所提系统需要通过较长的离线训练时间才能达到较优的检测性能，但可通过加载权重以及在线训练的方式完成系统部署，并根据实际信道环境调整权重参数，最终实现快速检测并获得良好的检测性能。

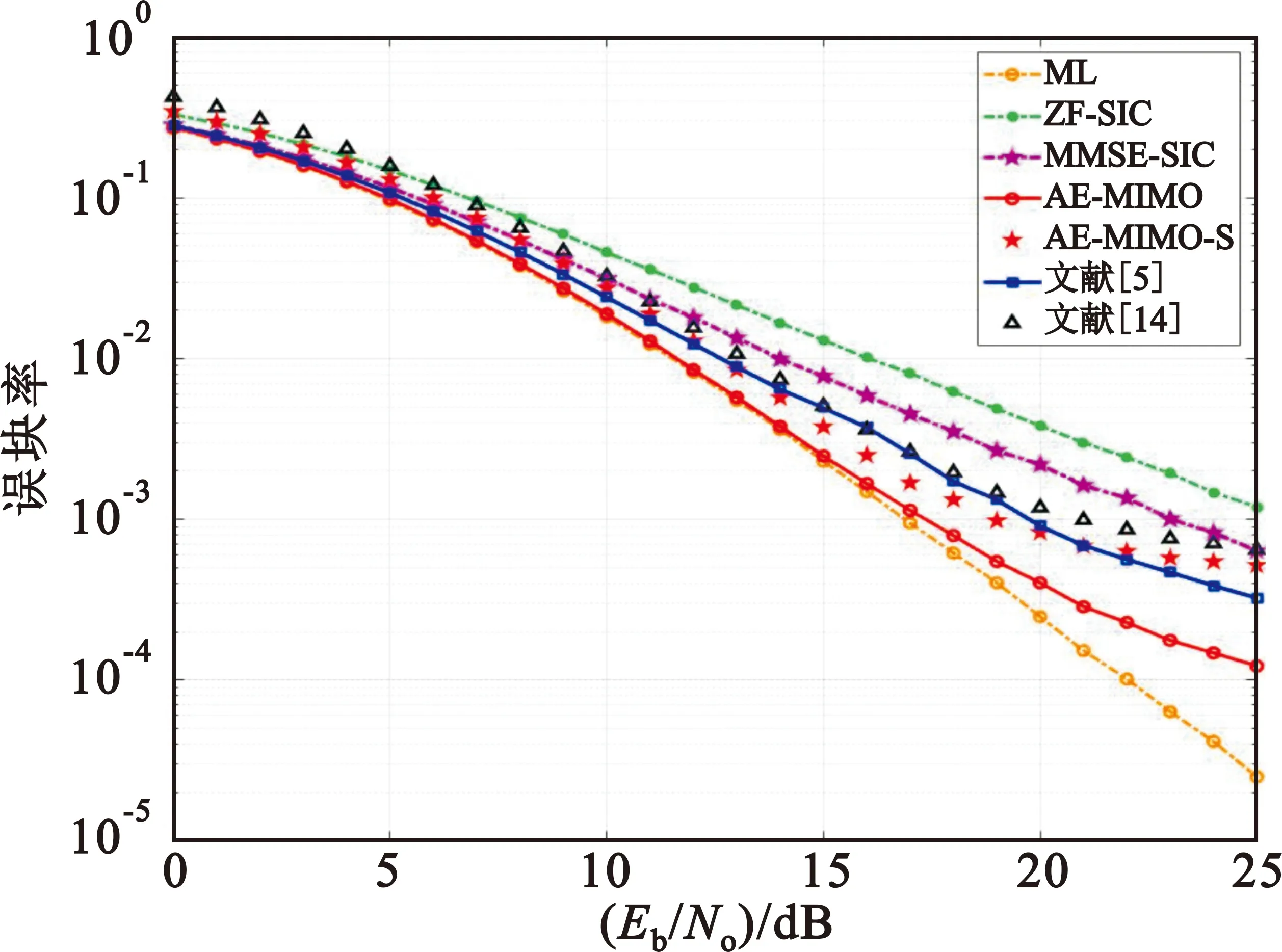
图6 QPSK调制下两发两收系统信号检测方案性能比较

表6 AE-MIMO系统与文献[5]、文献[14]系统参数对比

实验4 LTE-ETU信道模型下CNN-CE模块与不同信道估计算法进行信道估计性能与复杂度对比。

为了验证CNN-CE模块对于信道估计性能的提升，使用LTE-ETU模型进行信道建模。假设一帧数据由1个导频序列和3个数据序列所组成，本文利用四个数据帧内的导频序列对四个数据帧内的信道进行联合估计，将最终结果与基于导频的LS算法和MMSE算法相比较。如图7所示，在LTE-ETU信道下，CNN-CE模块估计得到的信道矩阵较两导频的LS估计法有5.5 dB左右的性能提升。相比于基于先进深度学习的信道估计算法[3]，本文提出的信道估计算法考虑到帧间信道信息的相关性，利用密集连接卷积网络的跨层连接和特征复用特性学习信道矩阵之间的相关信息，将噪声干扰尽可能地减少，并显著提高了信道估计的准确度。由于密集连接卷积网络的复用特征随着网络层数的加深而显著增加，因此本文提出的信道估计模型复杂度较高，具体系统参数对比如表7所示。

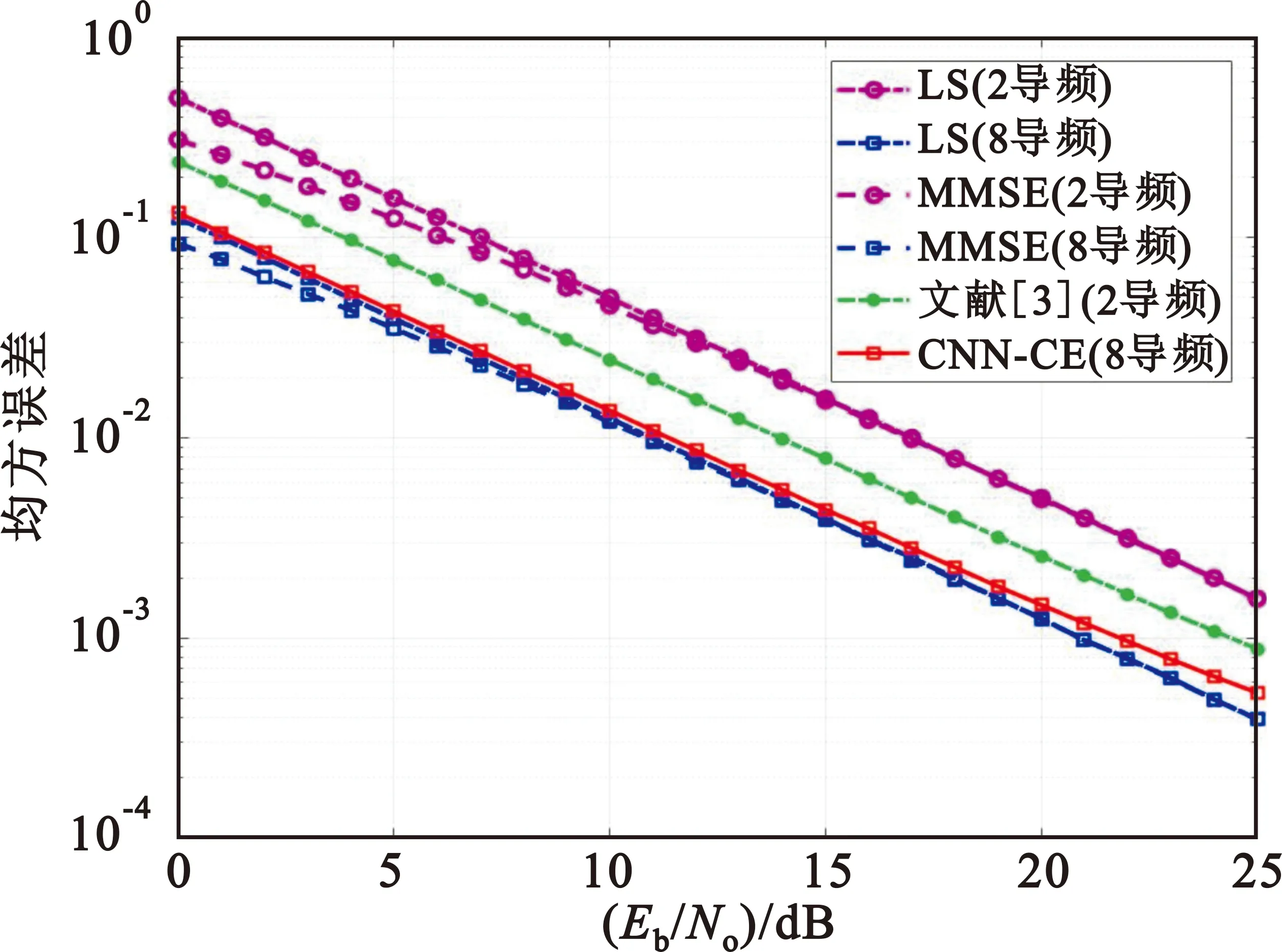
图7 两发两收系统不同信道估计方法性能比较

表7 CNN-CE模块与文献[3]系统参数对比

实验5 将CNN-CE模块与AE-MIMO系统结合，并在不同调制方式下与接收完美信道信息均衡处理的AE-MIMO进行性能比较。

为了检验CNN-CE模块所提供的信道估计结果对AE-MIMO系统性能的影响，采用两发两收的AE-MIMO系统进行VLST编码，将训练好的CNN-CE模块加载到AE-MIMO系统中，并将仿真结果与经过理想信道均衡的AE-MIMO系统进行对比。如图8所示，CNN-CE与AE-MIMO联合训练的系统误码性能与经过理想信道均衡的AE-MIMO系统仅有1 dB左右的性能误差。虽然实际的无线传播信道与训练信道模型可能存在差异，但是本文提出的系统可以通过权重加载以及在线训练，根据实际信道环境调整权重参数，降低训练模型与实际信道间差异造成的影响。