基于频谱形状的低复杂度雷达信号分类

2022-02-12尹良林睿王晓雷姚宇亮周林何元

电信科学 2022年1期

关键词：复杂度信噪比频谱

尹良，林睿，王晓雷，姚宇亮，周林，何元

研究与开发

基于频谱形状的低复杂度雷达信号分类

尹良1，林睿1，王晓雷2，姚宇亮1，周林1，何元1

（1. 北京邮电大学信息与通信工程学院，北京 100876；2. 军事科学院国防科技创新研究院，北京 100071）

为解决雷达信号调制识别中存在的计算复杂度高、低信噪比环境识别准确率低和仿真数据真实度低等问题，提出了基于频谱形状的低复杂度雷达信号分类算法。对信号频谱进行归一化，按频谱采样的方法提取特征参数，训练机器学习分类模型。雷达信号源生成数据的测试结果表明，本算法对Barker码、Frank码、LFM、BPSK、QPSK调制和常规雷达信号的分类准确率大于90%（SNR≥3 dB），计算复杂度低，能适应信号参数变化，具有很好的泛化性。

频谱形状；低复杂度；特征提取；频谱采样

0 引言

雷达信号识别技术在电子对抗和无线电监测领域都有着广泛的应用。脉内调制雷达信号的识别是雷达信号侦察的关键一环，关系着后续信号的参数估计，为情报获取和干扰等提供极大帮助，所以雷达信号分类算法的研究至关重要。随着电子信息技术的发展，新的雷达信号调制方式不断涌现，电磁环境日益复杂。传统雷达信号识别算法的局限性愈加突出，雷达信号的调制识别也面临新的挑战。

一直以来，雷达信号的脉内调制识别算法研究是学术界的热点和难点。文献[1]运用谱相关分析法，提出了4个相干特征参数，使用支持向量机（support vector machine，SVM）作为分类器完成了雷达信号的调制识别。文献[2]研究了小波变换算法中常用的Morlet小波方法。此类方法通过对信号进行小波变换，提取小波脊线作为特征进行脉内调制雷达信号的分类。但此方法需要选择合理的小波基，且小波脊线提取算法易受噪声干扰，实际应用效果不理想。文献[3]提出了以四阶和六阶累计量作为特征参数的识别算法，基于高阶累积量的调制识别算法对相关参数的扰动具有一定抗性，算法具有较好的稳健性。但上述算法都存在计算复杂、实时实现难度较大的问题。文献[4]提出基于相对无模糊相位重构的脉内调制雷达信号识别方法，但能识别的调制方式单一；文献[5]针对低信噪比环境改进了该算法，实现了当信噪比大于6 dB时，对二进制相移键控（binary phase-shift keying，BPSK）、四相移相键控（quadrature phase-shift keying，QPSK）、线性调频和双线性调频雷达信号的识别准确率高于90%；文献[6]通过提取信号频谱复杂度特征、信号平方频谱特征、谱峰特征以及最小二乘直线拟合方差特征，以4个特征参数为出发点设计的基于频谱复杂度的分类算法，在信噪比大于6 dB时，窄脉冲雷达信号识别准确率较高。文献[7]使用时频分析、图像处理和卷积神经网络技术进行雷达信号的调制识别，通过引入Cohen类时频分布和二重滤波、双线性插值等图像处理技术以获得高质量时频图像，但算法计算复杂度很高，卷积神经网络的训练需要数小时。文献[8]提取低复杂度的瞬时信号特征及其统计量作为特征向量，通过FPGA编程实现了6种雷达信号的实时调制识别，在信噪比大于7 dB时，识别准确率大于90%。近年来，深度学习在调制识别领域取得了很好的成果，但少有应用于实际硬件系统的深度学习实时调制识别系统，一方面是因为深度学习网络模型复杂度高，难以部署到实际的在线实时系统；另一方面是网络深度受硬件计算能力的限制，浅层网络识别准确率较低。文献[9]中基于软件无线电设备AD9361提取简单信号特征作为机器学习模型输入向量，对比了23种机器学习模型用于实时调制识别的效果，其中SVM的总体识别准确率最高，为86.3%，在信噪比大于15 dB时，识别准确率大于90%；文献[10]结合通用软件无线电外设（universal software radio peripheral，USRP）和GNU Radio实现了通信信号的实时调制识别，该调制识别系统离线训练残差网络（residual network，ResNet），使用训练好的网络模型进行在线预测，近似达到实时效果。该系统对于6种常见通信信号的总体识别准确率在信噪比大于8 dB时大于90%，在信噪比大于14 dB时大于96%。文献[11]提取信号瞬时特征训练神经网络模型，实现了7种通信信号的实时调制识别，在信噪比大于6 dB时，识别准确率大于90%。

综上所述，首先，传统的雷达信号分类算法多依赖于IQ基带信号的信号处理转换，计算复杂度高，且要求信号的参数满足一定条件，不能较好地解决低功耗终端限制下雷达信号的实时分类问题。目前的实时调制识别系统为了降低复杂度，通常提取简单的瞬时信号特征，但该类系统牺牲了抗噪性以提高识别准确率，需要在较高信噪比环境（一般大于6 dB）下才能保证较高的识别准确率。其次，上述研究多采用仿真软件生成雷达信号，没有考虑实际雷达信号监测时需要应对的接收机频偏和相偏等不理想因素，导致信号识别的理论仿真结果与实际工程实现存在一定的差距。本文的创新点是借助于图像处理中的形状识别，提取雷达信号的频谱形状作为信号的特征，通过将频谱图像标准化，解决了雷达信号参数变化的问题；通过对频谱下采样提取特征，计算复杂度低，并避免了传统方法对IQ时域信号处理需要考虑频偏和相偏等问题；采用半实物仿真方法采集数据，数据更加贴近实际工程场景。本算法能识别频谱形状存在较大差异的雷达信号，并不局限于固定几类调制方式的分类识别上。

实验结果表明，该算法实现了常规雷达信号、BPSK、QPSK、Barker码、Frank码和线性调频（linear frequency modulation，LFM）调制在信噪比（signal-noise ratio，SNR）大于3 dB环境下大于90%的分类准确率。该算法计算简单，只要频谱形状存在较大差异即可实现低信噪比环境下的正确分类，所以能够应用于多种调制方式雷达信号的分类识别。本文提出的信号频谱的预处理方法使得分类模型能适应多种参数下的雷达信号。其次，运用包含不同参数雷达信号的训练集训练的模型正确率较单一参数情况基本不变，模型泛化性较传统算法有很大提高。

1 雷达信号模型和数据集

表1 6种雷达信号的数学模型

为了模拟真实的雷达信号射频接收场景，本文使用安捷伦信号源N5182配合Keysight的软件Signal Studio for Pulse Building生成2 GHz的雷达信号，经过空中真实信道传输到达泰克6 114频谱仪，信号采集场景实物如图1所示，数据采集信息见表2。在MATLAB中对实际采集的高信噪比雷达信号使用AWGN函数仿真不同信噪比的噪声环境，本文主要研究了高斯白噪声对模型的影响。

图1 信号采集场景实物

表2 数据采集信息

2 基于频谱形状的雷达信号分类算法

根据不同调制方式的信号的频谱形状差异性，设计了基于频谱形状的分类算法。其计算复杂度低且具有一定的抗噪性能。本文算法的重点是提取频谱形状的差异性特征，并使该特征能适应雷达信号参数的变化。特征的有效性保证了算法的准确性，特征对雷达信号参数的适应性保证了算法更好的泛化性。本文提出了一种频谱的预处理方法，通过预处理能将不同参数雷达信号的频谱统一到相同的标准，且尽可能保证频谱形状基本不变。本文算法系统如图2所示，实际信号的处理流程如下。

步骤1 信号源发射各种雷达信号，频谱仪采集空中真实信号，完成射频信号的超外差变频接收，输出基带信号IQ数据至预处理模块。

步骤2 在预处理模块中，对基带信号IQ数据进行快速傅里叶变换（fast Fourier transform，FFT），通过滤波和归一化处理后得到统一标准的频谱形状图，输出至特征提取模块。

图2 本文算法系统

步骤3 在特征提取模块中，提取频谱形状的峰度、偏度以及归一化频谱采样幅值组成特征向量，作为分类器的输入。

步骤4 在训练阶段，分类器利用特征向量训练浅层神经网络；在测试阶段，分类器利用特征向量预测雷达信号调制方式。

2.1 预处理

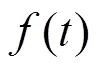
离散傅里叶变换，即连续傅里叶变换在时域和频域上的表示都是一种离散形式。离散傅里叶变换的表达式为：

本文预处理操作针对频谱，包含以下5个步骤。

步骤1 绘制频谱图。根据离散傅里叶变换相关原理，绘制雷达信号的频谱图，后续操作均为对频谱图的处理。信号序列由采集的雷达信号分割而成，每段序列长度为16 384点。

步骤2 取频谱包络，去除仪器噪声。采集的雷达信号包含一定的仪器噪声，其在频谱散点图中表现为分布在理想频谱包络内的散点。可以通过取频谱包络的方法去除大部分仪器噪声频谱。

步骤3 频谱幅值归一化。克服信号功率变化引起的幅值变化，也方便后续处理。这是机器学习对训练数据的要求，也有利于模型的泛化。

步骤4 截取频谱有效片段。通过截取频谱有效片段能去除频谱两端无用、甚至产生干扰的底噪频段，起到了滤波的作用。该过程的关键是选择合适的阈值，保证既去除频谱两端的噪声频段，又能最大化地保留雷达信号频谱形状的差异性。通过实验发现，选择固定阈值效果差，对不同调制方式的雷达信号不具有适应性。本文计算频谱数据的均值作为阈值，由于高斯白噪声均值近似为零，所以该阈值对白噪声不敏感。

步骤5 频谱归一化和插值。不同调制方式的信号通过前述方法截取频谱的频段长度不同，即频谱数据量不同。在同种调制方式中，随信号参数变化也会引起频谱带宽的变化，截取的频谱长度也会产生不同。因此为了保证后续特征提取更加快速有效地完成，需要将截取频段的频谱数据量统一到相同的标准。最好的办法是计算频谱曲线的具体方程，此过程通过插值完成。这里引入三次样条插值方法对截取的频段进行插值，将截取的频段数据量扩展到400个。

三次样条插值法具有计算简单、稳定性好、收敛性高且易在计算机上实现的优点。

故三次方程可以构造成如下形式：

这样可以构造一个以为未知数的线性方程组。

左侧的系数矩阵为严格对角占优矩阵，即每一行中对角元素的模值大于其余元素模值之和，故线性方程组有唯一解。

2.2 特征提取

特征提取从以下两方面考虑，一是频谱形状的统计特征，二是频谱的包络形状。对于统计特征，本文提取了频谱图中各频率位置的幅值的峰度和偏度作为特征向量。

对于频谱包络，采样是最直观的特征提取方法。通过采样，提取频谱形状差异性点位的幅值数据作为特征向量可以很好地区分频谱形状不同的各类雷达信号。此步骤的重点在于提取出这些表征不同形状差异性的点位。通过人工选取采样点费时费力且效果差，本文采用了对预处理的频谱下采样的方法，这一方法的依据是在采样点数足够多的情况下，必定能包含频谱形状的差异性点位。本文中通过下采样均匀采集了40个点，将其频谱数据作为特征向量用于训练分类器。频谱采样示意图如图3所示，将采样点的频谱幅值数据作为特征参数用于训练分类器。

2.3 分类器

人工神经网络是模仿生物神经网络的特征，通过对输入数据进行分布式并行处理，可以为分类等问题建立数学模型。神经网络的特点主要是非线性和自适应性，它通过简单的信息处理单元（神经元）的相互连接，并行地处理信息，最终通过神经元上的权重等相关参数完成学习、分类等任务。

本算法使用了浅层神经网络，该模型由MATLAB的模式识别工具箱（nprtool）提供。需设置的参数包含隐藏层数量和训练、验证、测试集比例。隐藏层数量越高，模型分类的非线性越好。在训练集的划分中，训练和验证集会参与模型学习的过程，决定模型训练阶段的准确率；测试集对模型的实质性能进行测试，评估训练阶段得到的模型泛化性。本文使用的浅层神经网络结构如图4所示。分类器的输入为经预处理后提取的特征向量（峰度、偏度及频谱形状特征），输出为雷达信号调制类型。通过实验，由分类准确率的高低确定了最优的隐藏层数量。当隐藏层为30层时，分类准确率最高。

图3 频谱采样示意图

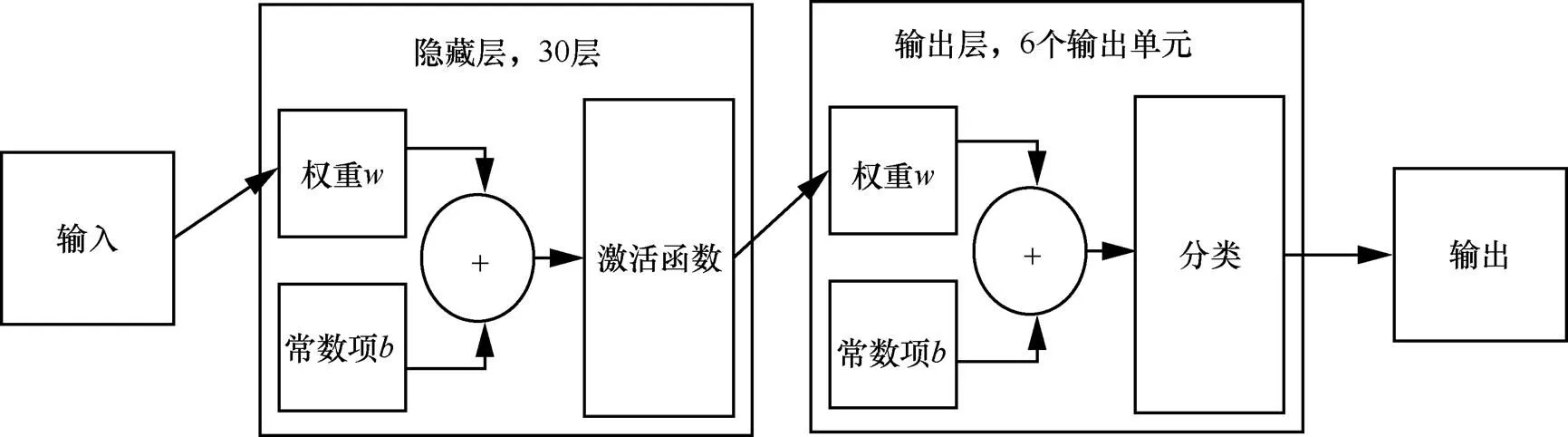
图4 浅层神经网络结构

2.4 复杂度分析

目前已发布的实时脉冲雷达信号调制分类器并不多。一般来说，由于缺乏信息重现其结果，很难比较不同的调制分类识别器的性能，此外，由于许多文献没有提出调制分类识别器的硬件和软件实现，因此，无法对实时性能进行分析[8]。为了进行公平的比较，在同样基于特征的调制分类识别器中，着重分析信号预处理及特征提取算法的复杂度。

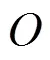
本文算法仅通过FFT提取特征向量，而其他调制分类识别器[12-15]为了获得更好的分类性能，以时频处理为代价，需要使用更复杂的算法。各调制分类器算法复杂度[16]见表3，抗噪性指示调制识别器的总体识别准确率大于90%的最低信噪比。

其中，代表分析点数，代表时间窗长点数。可以看到算法的复杂度都与分析窗长和离散时间点数有关。对比可知，FFT的算法复杂度最低，而Morlet小波算法复杂度比较高。本文算法使用了简单的信号特征和分类器，没有时频处理，代价是抗噪性降低，但与文献[8]中低复杂度实时调制分类系统相比，对于LFM、Barker码、Frank码调制类型的雷达信号，本文算法仍具有更高的识别准确率和抗噪性。

3 实验结果

为测试模型的抗噪性和泛化性设置对比实验，实验设置见表4。

使用相应测试集测试各组实验模型的性能。未做说明时，测试集大小为每种调制方式500个样本，共3 000个样本。实验1在第一组数据的测试集上有较高的分类准确率，对Barker码、Frank码和LFM调制的雷达信号的识别准确率大于98%（SNR≥0 dB）。实验2在第一组数据的测试集上有很高的分类准确率，不同信噪比测试集结果如图5所示。随信噪比降低，正确率降低，在信噪比大于10 dB时，正确率在97%以上，在0 dB信噪比下，正确率降低到86.8%。0 dB和10 dB环境测试集混淆矩阵分别见表5、表6，错误集中在BPSK和QPSK两种调制方式的识别上。这是由于这两种调制方式雷达信号的频谱形状相似，在低信噪比环境下，其频谱形状的差异性受到削弱，故分类准确率降低。

表3 各调制分类器算法复杂度

表4 实验设置

为了验证模型的泛化性，实验3在第一组、第二组及混合第一、二组数据的测试集上有很高的分类准确率，不同信噪比测试集结果如图6所示。该模型准确率较实验2测试结果基本不变，分类准确率大于90%（SNR≥4 dB）。模型能适应不同参数的雷达信号，其在不同参数的测试集上有较高的分类准确率，模型具有较好的泛化性能。

表5 实验2——0 dB环境测试集混淆矩阵

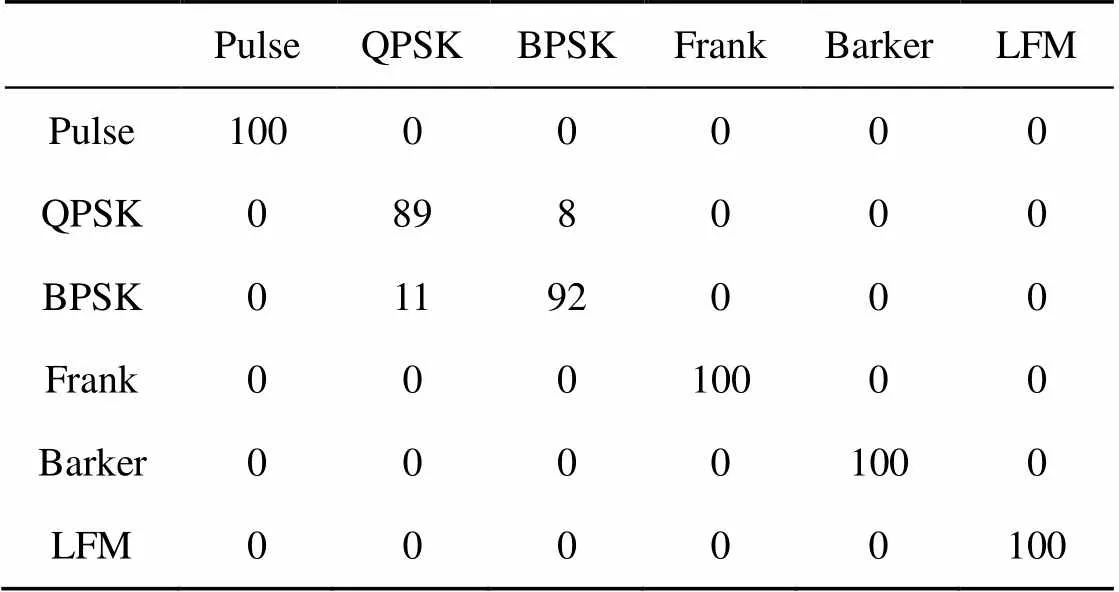
表6 实验2——10 dB环境测试集混淆矩阵

图6 实验3——不同信噪比测试集结果

本算法与文献[5]、文献[8]算法分类准确率对比如图7所示。本文算法实现了在更低信噪比的情况下，达到与文献[5]相同的分类准确率。本文算法针对频谱形状差异，对BPSK、QPSK调制方式的分类效果较差，原因是这两种调制方式的雷达信号频谱形状非常相似，受噪声影响时，随信噪比降低，其频谱形状的差异性受到削弱。但其余调制方式的分类准确率均高于文献[5]的算法，且本文算法能分类的调制方式更多，满足频谱形状存在较大差异即可，并不局限于固定的几种调制方式。对比同样使用低复杂度特征的文献[8]，本文算法的抗噪性能更好。在信噪比大于3 dB时，本文算法整体识别准确率大于90%，而文献[8]算法在信噪比大于7 dB时，整体识别准确率大于90%。

图7 本文算法与文献[5]、文献[8]算法分类准确率对比

4 算法优缺点讨论

应用图像处理中的形状识别，通过采样的方式提取各调制方式雷达信号频谱形状的差异性特征，计算复杂度低，且避免了传统方法中对IQ时域信号处理需要考虑的频偏和相偏等问题。该算法实现了低信噪比下不同参数雷达信号较高准确率的分类识别。其中通过预处理将目标频谱标准化，使得模型能适应雷达信号的参数变化。本文提出的频谱预处理方法的实践意义在于将信号频谱标准化，这种思想在提高模型泛化性能的研究中具有很大的潜力。但该算法在应对频谱形状相似的调制方式时效果不佳，可以与其他算法结合解决该问题。结果表明，该算法具有很好的泛化性。在低信噪比环境下，文献[5]提出的传统方法的分类准确率大于90%（SNR≥6 dB），文献[8]提出的低复杂度实时分类算法的分类准确率大于90%（SNR≥7 dB），本文算法实现了在SNR≥3 dB时，分类准确率大于90%。其次，本文算法针对频谱形状差异较大的雷达信号，对于Barker码、Frank码和LFM调制此类频谱差异较大的雷达信号的分类准确率很高，在0 dB环境也高于98%。这也说明本文算法并不局限于固定的几种调制方式，频谱形状存在较大差异是实现成功分类的主要条件。最后，实验结果表明，本文算法在训练集包含不同参数雷达信号时，分类准确率较单一参数情况基本不变，模型的泛化性高。

5 结束语

本文重点研究了基于频谱形状的低复杂度雷达信号分类算法，提出了频谱的预处理方法，可以将不同参数雷达信号的频谱统一到相同的标准。通过下采样的方式均匀采集频谱图相应点位数据作为特征参数，训练分类器实现雷达信号的分类。该算法具有较低的计算复杂度，便于使用FPGA编程实现。该算法具有较好的抗噪性能，信噪比大于3 dB时，分类准确率大于90%，且对Barker码、Frank码和LFM调制的雷达信号分类准确率大于98%（SNR≥0 dB），较目前实时调制识别算法在信噪比大于6 dB时信噪比大于90%的现状，本文算法在抗噪性上有较大提高。频谱形状差异是决定分类准确率的主要特征，因此该算法并不局限于固定的几种调制方式。其次，该算法具有很好的泛化性，能适应不同参数的雷达信号。在训练集混合不同参数雷达信号情况下，分类准确率基本不变，与此同时，模型泛化性提高。但本文算法对于频谱形状相似的雷达信号识别率较低（如BPSK和QPSK调制），可尝试融合多种特征进行调制识别。

[1] HU H, WANG Y J, SONG J D. Signal classification based on spectral correlation analysis and SVM in cognitive radio[C]//Proceedings of 22nd International Conference on Advanced Information Networking and Applications (AINA 2008). Piscataway: IEEE Press, 2008: 883-887.

[2] 王渝冲. 雷达信号调制类型识别与参数估计方法研究[D]. 长沙: 国防科学技术大学, 2012.

WANG Y C. Research on the modulation recognition algorithms and parameter estimation algorithms of radar signal[D]. Changsha: National University of Defense Technology, 2012.

[3] 冯祥, 李建东. 调制识别算法及性能分析[J]. 电波科学学报, 2005, 20(6): 737-740.

FENG X, LI J D. Modulation classification algorithms and performance analysis[J]. Chinese Journal of Radio Science, 2005, 20(6): 737-740.

[4] 黄知涛, 周一宇, 姜文利. 基于相对无模糊相位重构的自动脉内调制特性分析[J]. 通信学报, 2003, 24(4): 153-160.

HUANG Z T, ZHOU Y Y, JIANG W L. The automatic analysis of intrapulse modulation characte- ristics based on the relatively non-ambiguity phase restoral[J]. Journal of China Institute of Communications, 2003, 24(4): 153-160.

[5] 王丰华, 黄知涛, 姜文利. 一种有效的脉内调制信号识别方法[J]. 信号处理, 2007, 23(5): 686-689.

WANG F H, HUANG Z T, JIANG W L. An effectual approach of intra-pulse modulated signal recognition[J]. Signal Processing, 2007, 23(5): 686-689.

[6] 刘鲁涛, 戴亮军, 陈涛. 基于频谱复杂度的雷达信号调制方式识别[J]. 哈尔滨工程大学学报, 2018, 39(6): 1081-1086.

LIU L T, DAI L J, CHEN T. Radar signal modulation recognition based on spectrum complexity[J]. Journal of Harbin Engineering University, 2018, 39(6): 1081-1086.

[7] QU Z Y, HOU C F, HOU C B, et al. Radar signal intra-pulse modulation recognition based on convolutional neural network and deep Q-learning network[J]. IEEE Access, 2020(8): 49125-49136.

[8] IGLESIAS V, GRAJAL J, ROYER P, et al. Real-time low-complexity automatic modulation classifier for pulsed radar signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 108-126.

[9] VALIEVA I, BJÖRKMAN M, ÅKERBERG J, et al. Multiple machine learning algorithms comparison for modulation type classification for efficient cognitive radio[C]//Proceedings of MILCOM 2019 - 2019 IEEE Military Communications Conference. Piscataway: IEEE Press, 2019: 318-323.

[10] LIN C, YAN W J, ZHANG L M, et al. A real-time modulation recognition system based on software-defined radio and multi-skip residual neural network[J]. IEEE Access, 2020(8): 221235-221245.

[11] KALEEM Z, ALI M, AHMAD I, et al. Artificial intelligence-driven real-time automatic modulation classification scheme for next-generation cellular networks[J]. IEEE Access, 2021(9): 155584-155597.

[12] LUNDEN J, KOIVUNEN V. Automatic radar waveform recognition[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 124-136.

[13] 董志杰, 王晓峰, 田润澜. 雷达信号脉内调制识别新方法[J]. 航天电子对抗, 2018, 34(2): 33-37.

DONG Z J, WANG X F, TIAN R L. A new method of radar signal intrapulse modulation recognition[J]. Aerospace Electronic Warfare, 2018, 34(2): 33-37.

[14] 孟凡杰, 唐宏, 王义哲. 基于多特征融合的雷达辐射源信号识别[J]. 计算机仿真, 2016, 33(3): 18-22.

MENG F J, TANG H, WANG Y Z. Radar emitter signal recognition based on fusion of features[J]. Computer Simulation, 2016, 33(3): 18-22.

[15] 王渝冲, 宿绍莹, 陈曾平. 基于小波变换的雷达信号调制类型识别方法[J]. 计算机工程, 2012, 38(23): 166-168, 172.

WANG Y C, SU S Y, CHEN Z P. Method of radar signal modulation type recognition based on wavelet transform[J]. Computer Engineering, 2012, 38(23): 166-168, 172.

[16] 胡杨林. 跳频信号盲检测与参数盲估计算法研究及实现[D]. 成都: 电子科技大学, 2016.

HUYANG L. Frequency hopping signal detection and parameter estimation algorithm and implementation[D]. Chengdu: University of Electronic Science and Technology of China, 2016.

Low complexity radar signal classification based on spectrum shape

YIN Liang1, LIN Rui1, WANG Xiaolei2, YAO Yuliang1, ZHOU Lin1, HE Yuan1

1. School of Communication and Information Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China 2. National Innovation Institute of Defense Technology, Academy of Military Science, Beijing 100071, China

In order to solve the problems of high computational complexity, low recognition accuracy of low signal to noise ratio (SNR) environment and low fidelity of simulation data in radar signal modulation recognition, a low complexity radar signal classification algorithm based on spectrum shape was proposed. Signal spectrum was normalized, feature parameters were extracted by spectrum sampling method, and then machine learning classification model was trained. The test results of the data generated by the radar signal source show that the classification accuracy of Barker code, Frank code, LFM code, BPSK, QPSK modulation and conventional radar signals is more than 90% (SNR≥3 dB). The algorithm has low computational complexity, can adapt to the change of signal parameters, and has good generalization.

spectrum shape, low complexity, feature extraction, spectrum sampling

TN971.+1

10.11959/j.issn.1000−0801.2022011

2021−08−20；

2022−01−09

王晓雷，18610763901@163.com

国家自然科学基金青年基金资助项目（No.61801034）；国家重点研发计划项目（No.2018YFB1800802）

The National Nature Science Foundation Youth Fund of China (No. 61801034), The National Key Research and Development Program of China (No.2018YFB1800802)

尹良（1983−），男，博士，北京邮电大学副教授、硕士生导师，主要研究方向为信号检测与估计、软件无线电、机器学习在信号识别中的应用、无线电频谱工程半实物仿真。