交直流配电网小信号模型和直流侧低频振荡分析

陈庆， 范栋琛， 王晨清， 刘文凯， 袁晓冬， 袁小明

(1. 国网江苏省电力有限公司，江苏 南京 210024；2. 国网江苏省电力有限公司电力科学研究院，江苏 南京 211103；3. 强磁场工程与新技术国家重点实验室(华中科技大学)，湖北 武汉 430074)

0 引言

交直流配电网具有输送功率灵活可控、紧急状态下可提供快速跨区功率支撑等诸多优势，工程应用极为广泛[1—2]。然而，随着电力电子设备的大量接入，系统动态稳定性问题日益突出。在某实际交直流配电网调试过程中，出现了直流侧低频振荡现象。文中针对该问题对交直流配电网的稳定性进行分析，以期为后续交直流配电网工程的调试及运行提供参考。

小信号稳定性分析是研究动态稳定性的常用方法之一，可利用状态空间、特征值分析等方法研究系统遭受小扰动后保持稳定运行的相关问题。特征值分析法在小扰动稳定性分析方面得到广泛应用，文献[3—5]均利用特征值分析法分析不同控制参数对系统稳定性的影响。针对含电力电子设备的系统振荡问题，文献[6—7]指出大量负载通过DC/DC或AC/DC变换器接入电力系统，导致系统阻尼不足，从而引发直流电压自激振荡。文献[8]指出恒功率负载可能导致微电网主母线电压出现明显振荡或崩溃。文献[9]将变流器控制与机网振荡的多种模态联系起来，研究控制参数对振荡模态的影响。文献[10]指出由于LC滤波器输出阻抗和LC滤波器输入负阻抗在工作点附近的相互作用，输入电压可能出现振荡。文献[11]通过在控制环节增加虚拟电阻，抑制交直流变换器输出LC滤波器的振荡。综上所述，系统的振荡问题在实际运行中时有发生，不同因素影响系统振荡的规律也不尽相同。不同的硬件结构、不同的控制参数和不同的控制策略都会影响振荡的变化规律。然而，目前关于交直流配电网低频振荡的研究较少，其发生原因及影响规律亦较少涉及。因此，文中从实际交直流配电网直流侧出现的4 Hz左右低频振荡现象出发，在小信号建模基础上，对交直流配电网的稳定性进行分析。

为了深入研究影响该低频振荡的主要因素，并提出合理的抑制措施，文中从电网强度、功率水平、控制参数3个方面，讨论其对系统稳定性的影响，并从改变控制器参数和附加控制器2个角度，研究低频振荡抑制措施。文中研究内容对交直流配电网稳定性分析具有重要的参考价值。

1 交直流配电网及其小信号模型

1.1 交直流配电网模型

文中涉及的交直流配电网简化模型如图1所示。该模型共有4个端口，分别为交流端口AC 10 kV、AC 380 V以及直流端口DC 750 V、DC 375 V。10 kV交流母线经过电力电子变压器(power e-lec-tro-nic transformer，PET)主阀塔得到750 V直流电压，PET主阀塔采用级联H桥(cascaded H-bridge，CHB)+隔离型双向有源桥(dual active bridge，DAB)结构，该结构由5个相同的CHB和DAB构成，如图2所示。DC 750 V有2个出口，一个接电压源型变换器(voltage source converter，VSC)VSC1后回到10 kV交流母线;另一个接三相Buck变换器至DC 375 V，再接VSC2至AC 380 V交流母线。当三相Buck变换器的功率不断增大至超过额定功率时，375 V直流侧将发生4 Hz低频振荡现象。

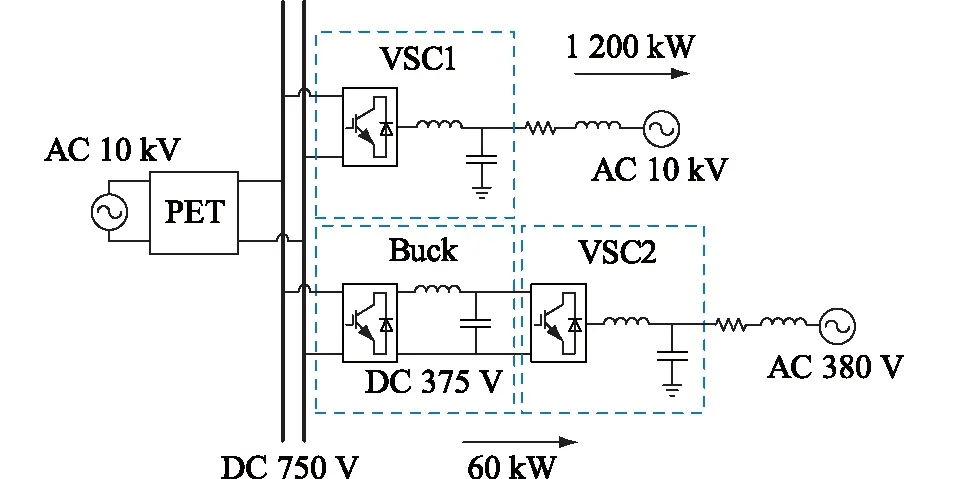
图1 交直流配电网简化模型Fig.1 The simplified model of AC/DC distribution network

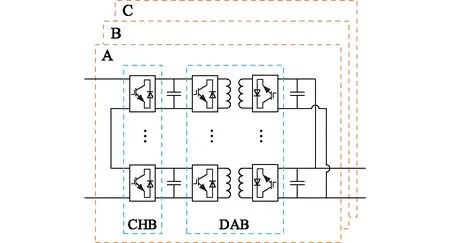
图2 PET主阀塔结构Fig.2 The structure of the PET main valve tower

1.2 交直流配电网小信号模型

建立交直流配电网的小信号模型，如图3所示。将某一非线性系统在工作点处进行线性化，形式如式(1)所示。

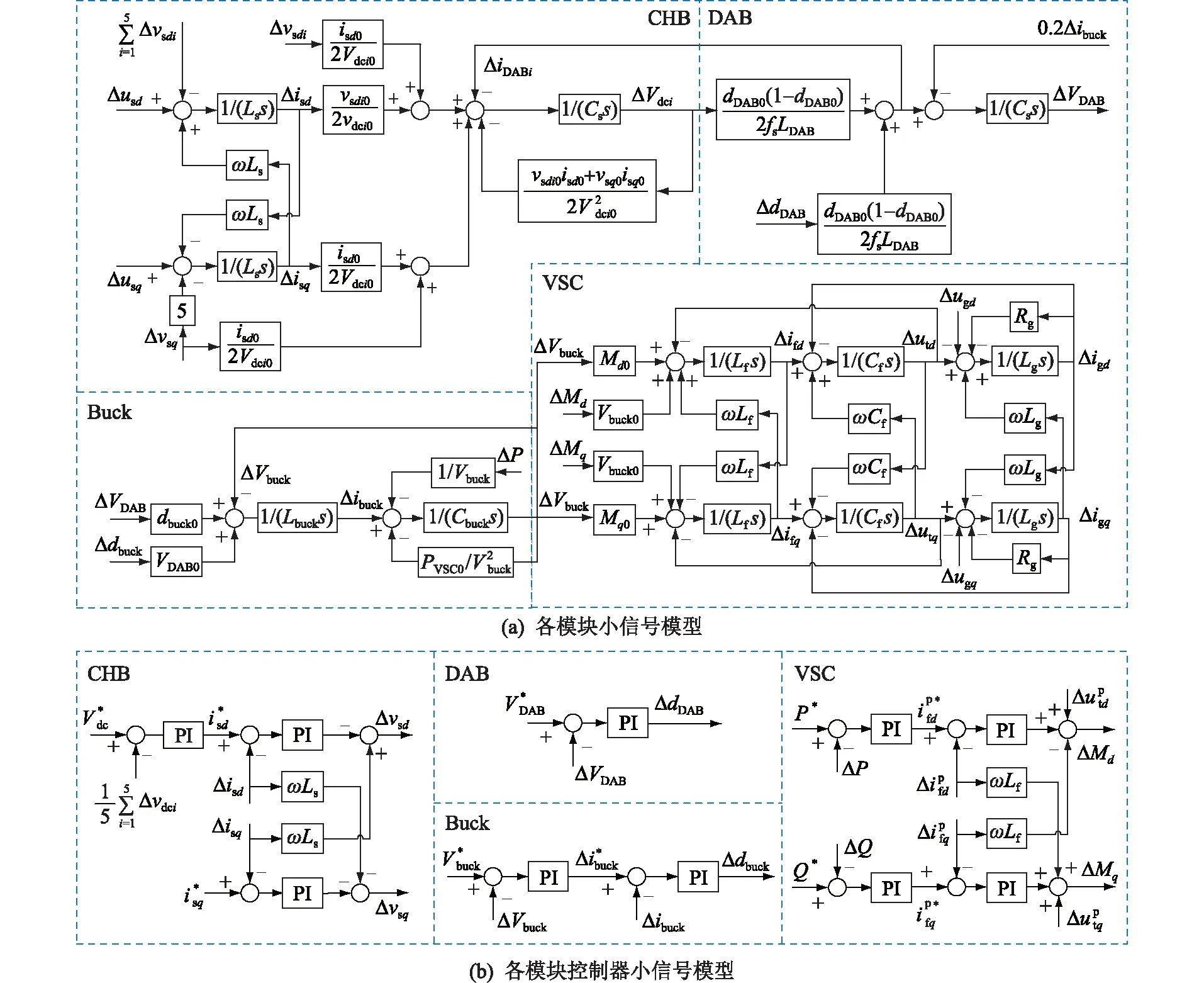
图3 交直流配电网小信号模型Fig.3 The small signal model of AC/DC distribution network

(1)

式中：x为系统的状态向量；y为输出向量；u为系统的输入向量；A为状态矩阵；B为输入矩阵；C为输出矩阵；D为前馈矩阵。

特征值分析法需要求解出状态矩阵A的特征值，再根据特征值判断系统的稳定性。文中将根据特征值分析方法，给出交直流配电网中各个模块的特征方程。

1.2.1 CHB小信号模型

CHB电气部分的线性化方程为：

(2)

式中：ω为工频角频率；Ls为CHB输入侧接入的电感；C1为CHB输出侧的并联电容；usd，usq分别为输入交流电源d、q轴直流电压；vsd，vsq分别为CHB输入端口d、q轴直流电压；vsd0，vsq0分别为vsd，vsq的稳态工作点；isd，isq分别为图2中CHB输入端口d、q轴直流电流；isd0，isq0分别为isd，isq的稳态工作点；Vdci为CHB中第i(i=1，2，…，5)级H桥的输出端口直流电压；Vdci0为Vdci的稳态工作点；iDABi为CHB中第i级H桥对后一级DAB的输入电流。

CHB控制器的线性化方程为：

(3)

CHB均压控制的线性化方程为：

(4)

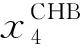
在CHB的小信号模型中，对应式(1)的状态变量ΔxCHB为：

ΔxCHB=

(5)

输入变量ΔuCHB为：

ΔuCHB=[ΔusdΔusqΔiDABi]T

(6)

输出变量ΔyCHB为：

(7)

结合式(2)—式(7)，得到CHB小信号模型为：

(8)

式中：A1，B1，C1，D1分别对应CHB小信号模型的状态矩阵、输入矩阵、输出矩阵、前馈矩阵。

1.2.2 DAB小信号模型

DAB电气部分的线性化方程为：

(9)

式中：LDAB为DAB中变压器原边的串联电感；C2为DAB输出侧的并联电容；VDABi为DAB中第i(i=1，2，…，5)级的输出电压；dDAB为DAB控制器得到的占空比；dDAB0为dDAB的稳态工作点；ibuck为DAB输入到后一级Buck变换器的电流；fs为DAB的开关频率。

DAB控制部分的线性化方程为：

(10)

式中：x为DAB控制器PI的积分器输出变量；kp，ki分别为DAB控制器PI的比例系数和积分系数。

在DAB小信号模型中，对应式(1)的状态变量ΔxDAB为：

ΔxDAB=[ΔVDABiΔx]T

(11)

输入变量ΔuDAB为：

ΔuDAB=[ΔVdciΔibuck]T

(12)

输出变量ΔyDAB为：

ΔyDAB=[ΔiDABiΔdDAB]T

(13)

结合式(9)—式(13)，得到DAB小信号模型为：

(14)

式中：A2，B2，C2，D2分别为DAB小信号模型的状态矩阵、输入矩阵、输出矩阵、前馈矩阵。

1.2.3 三相Buck变换器小信号模型

三相Buck变换器电气部分的线性化方程为：

(15)

式中：Lbuck，Cbuck分别为Buck变换器的滤波电感和电容；VDAB为DAB到Buck变换器的输入电压，此处假定DAB各级输出电压相同；ibuck为流过Buck变换器的电流；Vbuck为Buck变换器的输出直流电压；Vbuck0为Vbuck的稳态工作点；dbuck为Buck控制器得到的占空比；dbuck0为dbuck的稳态工作点；PVSC为Buck变换器输入到下一级VSC的输入功率；PVSC0为PVSC的稳态工作点。

三相Buck变换器控制部分的线性化方程为：

(16)

在三相Buck变换器的小信号模型中，对应式(1)的状态变量Δxbuck为：

(17)

输入变量Δubuck为：

Δubuck=[ΔVDABΔPVSC]T

(18)

输出变量Δybuck为：

(19)

结合式(15)—式(19)，得到三相Buck变换器小信号模型为：

(20)

式中：A3，B3，C3，D3分别为三相Buck变换器小信号模型的状态矩阵、输入矩阵、输出矩阵、前馈矩阵。

1.2.4 VSC小信号模型

VSC电气部分的线性化方程为：

(21)

式中：Lf，Cf分别为VSC的滤波电感和电容；Rg，Lg分别为无穷大电源的内电阻和内电感；Md，Mq分别为调制占空比的d、q轴分量；Md0，Mq0分别为Md，Mq的稳态工作点；ifd，ifq分别为流过滤波电感的d、q轴直流电流；utd，utq分别为VSC输出端电压的d、q轴分量；igd，igq分别为并网后流入无穷大电网的电流d、q轴分量；ugd，ugq分别为并网后无穷大电网的电压d、q轴分量。

VSC控制部分的线性化方程为：

(22)

在VSC的小信号模型中，对应式(1)的状态变量ΔxVSC为：

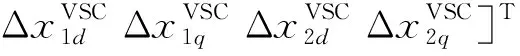
(23)

输入变量ΔuVSC为：

ΔuVSC=[ΔVbuckΔPΔQ]T

(24)

输出变量ΔyVSC为：

(25)

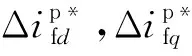
结合式(21)—式(25)，得到VSC小信号模型为：

(26)

式中：A4，B4，C4，D4分别为VSC小信号模型的状态矩阵、输入矩阵、输出矩阵、前馈矩阵。

2 系统低频振荡影响因素分析

基于上述分析，研究375 V直流侧出现低频振荡的原因，利用特征值分析法分别从电网强度、功率水平、控制参数3个方面，分析不同条件下375 V直流侧低频振荡时特征值的变化情况，得出不同因素对振荡的影响规律。仿真参数如表1所示。

表1 仿真模型主要参数Table 1 Main parameters of simulation model

2.1 电网强度

电网强度又称短路比(short circuit ratio，SCR)，其定义为[12—14]：

(27)

式中:Sac为交流短路容量；PdN为额定直流输送功率；UN为直流馈入点的交流额定电压；Z为交流系统等效电抗(忽略线路电阻)。

电网强度用于区分交流系统的强弱，是影响含电力电子设备的交直流配电网稳定性的一个重要因素，电网强度越强则系统越稳定。380 V交流侧fSCR的变化，影响375 V直流侧电压和VSC端电压的主要特征值，如图4所示。由图4可知，随着fSCR逐渐变小，VSC端电压主要特征值的阻尼系数逐渐变小、振荡系数逐渐变大。当fSCR由3变到1时，特征值从左半平面穿越至右半平面，系统失稳，表现为幅值增大的振荡。而375 V直流侧电压的主要特征值在fSCR不断变化时并无较大变化，即380 V交流侧fSCR对375 V直流侧电压影响不大。因此，380 V交流侧在弱电网强度下，只会使VSC端电压发生振荡，375 V直流侧电压仍可以保持稳定。

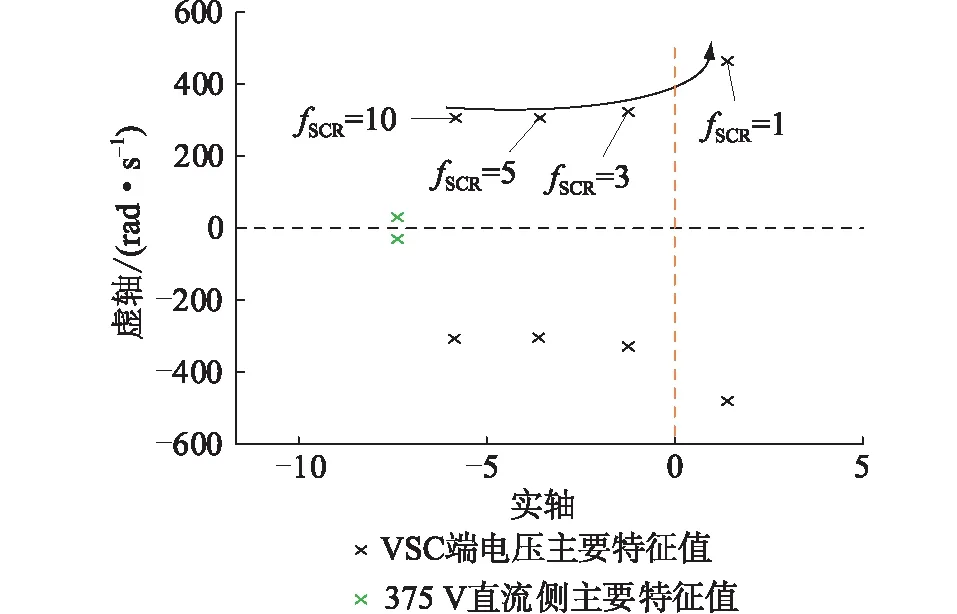
图4 不同fSCR下主要特征值的变化趋势Fig.4 The variation trend of the main eigenvalues under different fSCR

若0～3 s时，fSCR为3，3 s 后fSCR变为1，VSC端电压d轴分量的波形如图5所示。由图5可知，当380 V交流侧fSCR为3时，电压波形不变。380 V交流侧fSCR变为1后，即3 s后电压波形发生振荡，这与图4中主要特征值从左半平面穿越到右半平面的结果一致，验证了上述分析的正确性。

图5 不同fSCR下VSC端电压d轴分量波形Fig.5 The d-axis component waveform of VSC terminal voltages under different fSCR

2.2 功率水平

在实际交直流配电网运行过程中，375 V直流侧功率增大时会发生低频振荡，因此375 V直流侧功率是影响低频振荡的重要原因。不同功率水平下，系统主要特征值随功率的变化情况如图6所示。

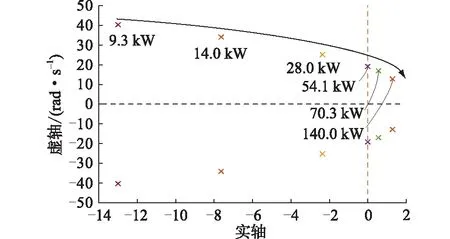
图6 功率水平变化时主要特征值的变化趋势Fig.6 The variation trend of the main eigenvalues with the change of power levels

由图6可知，特征值的振荡频率和阻尼系数均会随着功率的增大而减小，当功率大于54.1 kW时，特征值从左半平面穿越至右半平面，系统失稳，表现为幅值增大的振荡。因此，为确保系统的稳定运行，应尽量保证运行功率在额定功率以下。

功率水平是影响系统稳定性的一个重要因素，当375 V直流侧的运行功率超过额定功率时，系统失稳，呈现不同程度的振荡。0～5 s时，系统处于稳定状态，0.5 s时将375 V直流侧的功率从原先的9.3 kW分别提升至14.0 kW，54.1 kW，70.3 kW，观察3种功率水平下直流电压的波形变化，如图7所示。结合图6中特征值随功率水平的变化可知，功率从9.3 kW增加至14.0 kW时，系统的主要特征值仍在左半平面，系统仍保持稳定，即图7中0.5 s后，电压经过一段动态过程后仍恢复稳定。当功率从9.3 kW增加至54.1 kW时，系统的主要特征值位于虚轴，系统发生等幅振荡，即图7中0.5 s后，电压波形发生等幅振荡，频率约为4 Hz。功率从9.3 kW增加至70.3 kW时，系统特征值位于右半平面，系统失稳，即图7中0.5 s后，电压波形发生幅值不断增大的振荡。

图7 不同功率水平下375 V直流侧电压波形Fig.7 Waveforms of the 375 V DC side voltageunder different power levels

2.3 控制参数

2.3.1 Buck变换器电流内环PI控制器积分系数

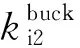
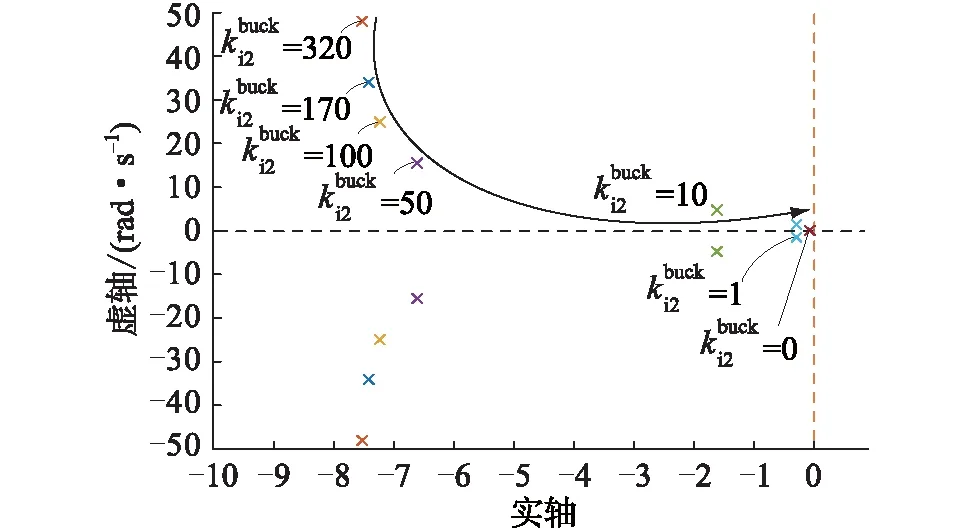
图变化时主要特征值的变化趋势Fig.8 The variation trend of the main eigenvalues with the change of

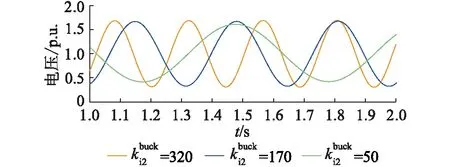
图对375 V直流侧电压波形的影响Fig.9 The influence of on the 375 VDC side voltage waveform

2.3.2 Buck变换器电压外环PI控制器比例及积分系数

图变化时主要特征值的变化趋势Fig.10 The variation trend of the main eigenvalueswith the change of

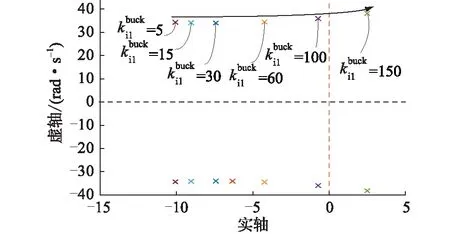
图变化时主要特征值的变化趋势Fig.11 The variation trend of the main eigenvalues with the change of

电压外环PI控制器比例及积分系数变化时，375 V直流侧电压波形的变化情况如图12所示。

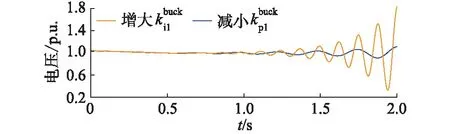
图12 电压外环PI控制器参数对375 V直流侧电压波形的影响Fig.12 The influence of voltage outer loop PI controllerparameters on 375 V DC side voltage waveform

3 直流侧低频振荡抑制策略

目前电力电子装备中振荡问题的主要解决方法有改进硬件结构、改变控制参数和改进控制措施3种[9,15—19]。其中，改进硬件结构在实际工程中难以应用，所以一般不采纳。电力电子装备的运行离不开控制器的设计，控制器参数直接影响了装备的稳定性，改变控制参数的方法可以在不改变装备硬件和控制器结构的情况下削弱振荡，但大量的模态分析会增加工作量，且参数的多样化使得分辨哪些参数起主导作用变得更为困难，有时改变参数也并不能抑制振荡发生。改变控制策略的方法往往行之有效，通过在现有控制方法下增加附加控制器，起到抑制振荡的作用。附加控制器的加入可以使系统的阻尼增加，提高系统的小扰动稳定性。文中将分别从改变控制器参数和增加附加控制器2个方面，提出抑制交直流配电网低频振荡的措施。

3.1 基于改变控制器参数的振荡抑制策略

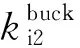
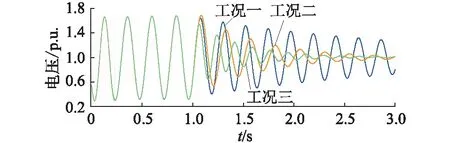
图13 改变电压外环PI控制器参数对375 V直流侧振荡抑制的效果Fig.13 The effect of changing the parameters of the voltage outer loop PI controller on 375 VDC side oscillation suppression

3.2 基于附加控制器的振荡抑制策略

电力系统稳定器(power system stabilizer,PSS)是最常见的附加控制器，其通过附加稳定信号控制励磁对发电机转子振荡提供阻尼。文中参照PSS原理设计附加控制器，即在Buck变换器的控制器侧增加附加控制器，如图14所示。

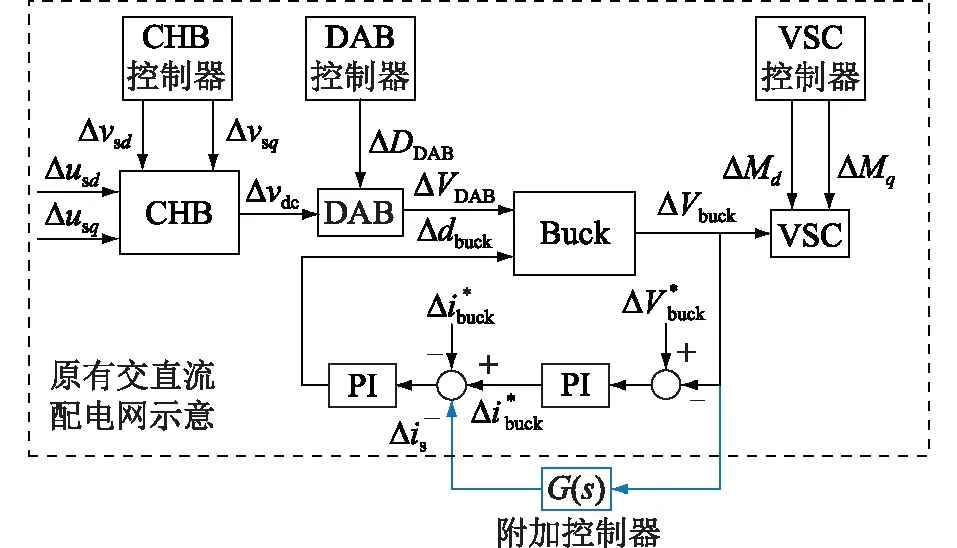
图14 含有Buck附加控制器的交直流配电网示意Fig.14 The schematic diagram of AC/DC distribution network with the Buck additional controller

Buck变换器采用电压外环和电流内环控制方式，其中低频振荡发生在375 V直流侧，采集该直流侧的振荡电压作为输入源，经过附加控制器G(s)，得到附加控制信号Δis，将该附加控制信号添加至控制器的电流比较环节，增加整个交直流配电网的阻尼，从而对振荡进行抑制。G(s)表达式为：

(28)

分别得到G(s)加入前后的主要特征值分布，如图15所示。可以看到，主要特征值将从右半平面穿越到左半平面，系统重新回到稳定状态。

图15 G(s)加入前后主要特征值变化趋势Fig.15 The variation trend of main eigenvaluesbefore and after G(s) is added

G(s)加入前后的低频振荡波形对比如图16所示。2 s前系统稳定运行，直流侧电压波形无振荡， 2 s时激发振荡，直流侧电压波形表现为低频振荡， 3 s时加入G(s)，直流侧电压波形经过短暂的动态过程后恢复稳定。可见，该附加控制有效，能够对振荡起到抑制作用。

图16 G(s)加入前后375 V直流侧电压变化情况Fig.16 The variation of the voltage on the 375 V DC side before and after G(s) is added

4 结论

文中基于某实际交直流配电网工程的小信号模型，开展了其在小扰动下的稳定性分析，明晰了其375 V直流侧低频振荡发生机理。通过理论分析和仿真实验，验证了电网强度、功率水平和控制参数对直流侧低频振荡的影响，最后通过改变参数和增加附加控制器对该低频振荡进行抑制，结论如下：

(1) SCR影响系统的稳定性。当380 V交流侧SCR变小时，VSC端电压将发生振荡，但对375 V直流侧影响不大。

(2) 功率水平是影响375 V直流侧低频振荡的重要因素。当375 V直流侧功率不断增大至超过额定功率时，将会发生低频振荡，因此在实际运行中，应尽量保证系统工作在额定功率以内。

(3) 控制参数影响系统的稳定性。Buck变换器电流内环PI控制器积分系数不影响系统的稳定性，但影响振荡发生后的振荡频率。Buck变换器电压外环PI控制器比例系数过小或积分系数过大会造成系统不稳定，因此在运行中应保证二者在合理范围内。

(4) 文中从控制器参数和附加控制器两方面，提出了抑制低频振荡的措施。增大Buck变换器电压外环PI控制器的比例系数和减小Buck变换器电压外环PI控制器的积分系数，可以有效抑制低频振荡。在Buck变换器的控制器侧增加附加控制器，可以增大系统阻尼，抑制375 V直流侧的低频振荡。

本文得到国网江苏省电力有限公司科技项目“多端口交直流混合配电网的系统稳定机理研究”(J2020078)资助，谨此致谢！