极端灾害下考虑动态重构的微网形成策略
2022-02-12张瑞曦徐青山程煜宋菁
张瑞曦, 徐青山, 程煜, 宋菁
(1. 东南大学电气工程学院,江苏 南京 210096;2. 南京南瑞继保电气有限公司,江苏 南京 211102)
0 引言
近些年,全球范围内的极端气象频繁发生,造成大规模停电及经济损失,这使得配电网应对极端自然灾害的能力得到广泛关注[1—2]。配电系统在台风、地震等极端自然灾害下,元件故障率大幅度升高,严重影响供电的安全性和可靠性[3]。而随着燃气轮机[4]、燃料电池等可控分布式电源(distributed generation,DG)的不断发展,其在极端事件下对重要负荷的支撑作用也逐渐被发掘。
可控DG需通过微网的方式,对脱离主网的负荷进行应急供电[5],并在灾害中合理重构,尽可能提高过程中恢复负荷的总价值,如此才能体现对重要负荷的支撑作用。微网的重构分成了静态和动态2种方式[6]。静态重构,即在一个负荷断面上对微网的结构进行优化。文献[7]采用静态重构的方法,选取负荷的额定值作为负荷断面,优化区域孤立状况下的静态重构方案。负荷一般不会超过额定值,因此该方法具有良好的适应性和稳定性,但当负荷与额定值偏差较大时,该方法灵活性较差,优化的结果也并非是最优解。动态重构,通常采用分段的方法,将动态重构问题转化为若干静态重构问题。文献[8]提出了基于信息熵的日负荷曲线分段方法;文献[9]采用聚类的方法,通过比较相邻时刻负荷所属类别来划分时段;文献[10—12]通过比较相邻时段的判断量和阈值大小来合并时段,判断量包括网损标准差、功率矩以及切换收益等。
上述配电网动态重构研究大多在正常运行状态下,以网损最小为优化目标。而在极端灾害条件下,以恢复负荷价值最大为优化目标的动态重构存在2个问题:一是极端灾害条件下的负荷由多个DG供电,微网结构受其空间分布影响较大,且目标函数具有较强的个体敏感性,因此不能采用负荷整体变化状况划分重构时段;二是微网电源功率不足,决策偏于保守,预测值与实际值可能存在较大差别,负荷值应以该时段负荷的最大值为准,而不是平均值。因此在时段划分时,不能简单考虑负荷的平均值,而应考虑某时刻负荷的概率分布情况。
文中在极端灾害的场景下研究配电网动态重构策略,充分考虑负荷个体的状态变化,将基于Wasserstein距离的负荷状态划分与静态断面优化相结合,形成动态重构的最优方案。此方案在提升重构灵活性的同时保留决策的保守性,提升了配电网在极端环境下的系统性能。
1 负荷状态的划分方法
1.1 划分步骤
在极端灾害条件下,以额定功率作为决策输入量的微网静态重构方法缺乏灵活性,因此提出了一种微网动态重构方法。考虑到多电源供电的微网结构受负荷空间分布的影响较大,以及恢复负荷价值最大这一目标函数的个体敏感性,文中所提的状态划分以单一负荷为划分对象。另外,考虑到极端灾害条件下决策的保守性和预测曲线偏差所带来的风险,文中通过研究负荷概率分布的变化代替预测曲线的变化,确定状态划分时刻。
负荷状态的划分步骤包括:(1) 选取典型灾害日的负荷样本,例如针对广东地区台风天气,选取台风频发的7月至9月的历史负荷数据作为样本;(2) 将用电量最小值至最大值之间分成若干等分;(3) 计算全天每个小时的概率分布;(4) 计算相邻小时概率分布的Wasserstein距离大小,将距离较小的小时合并,将距离较大的小时分开,完成对负荷状态的划分。
1.2 Wasserstein距离计算原理
Wasserstein距离,又称推土机距离,指的是把概率分布q转换为p的最小传输质量,用于衡量2个概率分布之间的差异[13],广泛应用于计算机科学[14]、图像识别[15]等领域。传统的欧式距离,通过对2条曲线对应位置的差值平方和取平方根来衡量距离大小。但当2条曲线距离较远、没有重叠或重叠较少时,欧式距离无法反映p,q分布之间的相对位置关系。因此,文中引入Wasserstein距离,通过研究概率分布的变化来解决负荷概率分布距离的问题。每小时的负荷概率分布建模为离散分布,离散分布的Wasserstein距离计算过程如图1所示。
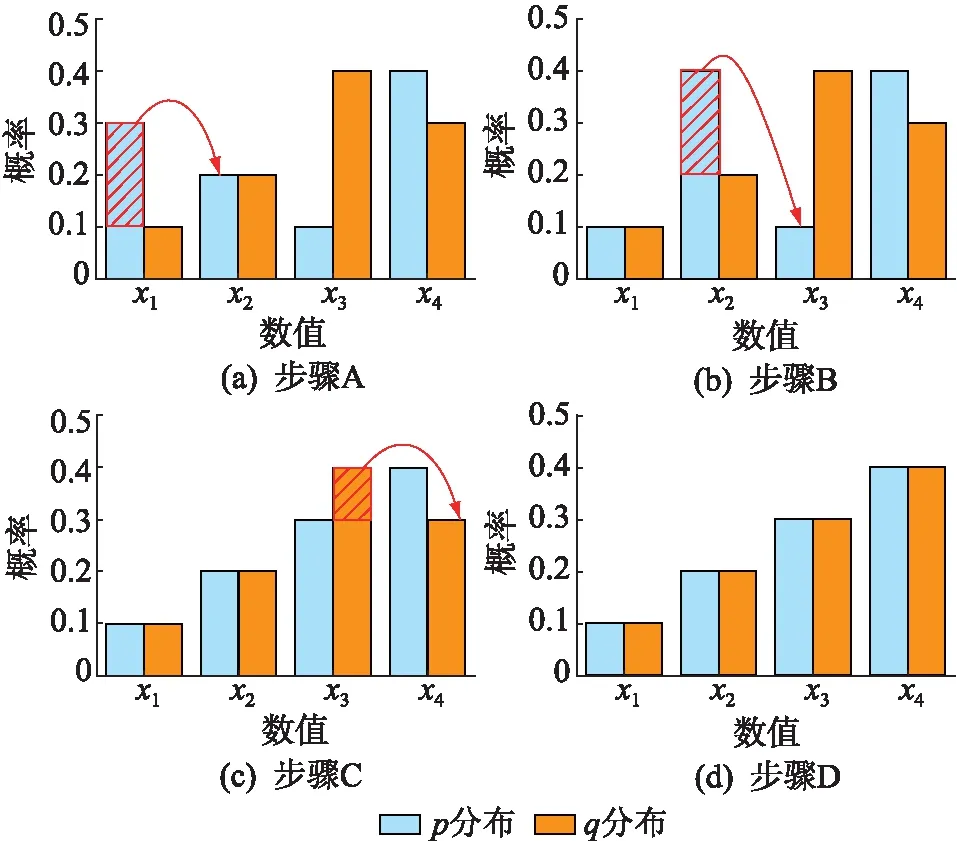
图1 离散分布Wasserstein距离计算过程Fig.1 Process of Wasserstein distance calculation between discrete distributions
计算每一个步骤需要移动的“质量”再乘以该步骤移动的“距离”,最后将这些乘积求和,便可获得将分布p与分布q“推”成相同分布所要做的“功”,从而反映2个分布之间的差异。
1.3 负荷状态划分算例
选取灾害典型月份的某负荷30 d样本,将负荷最小值和最大值之间划分为10个区间,离散化负荷概率分布如图2所示,其中,①~⑩为区间编号。

图2 概率分布的区间划分Fig.2 The interval division of probability distribution
由图2可见,样本在00:00—10:00及20:00之后,负荷集中在下方4个区间,而在10:00—20:00集中于上方6个区间,反映了负荷的用电习惯。
假设用户1 h内的用电状态相同,将每15 min计量一次的样本数据,按照每小时统计一个概率分布,部分时段的概率分布如图3所示。

图3 24 h负荷概率分布Fig.3 Load probability distributions of 24 hours
图3中,区间对应图2中有功功率从最大值到最小值划分的10个部分,概率为图2中的点落在各个区间内的占比。图3描绘了用户1 d用电水平的状态变化,早间时段负荷主要分布于功率水平较低的区间,午间时段负荷逐步转移到水平较高的区间,而晚间时段负荷分布返回水平较低的区间,同时体现了各时段内负荷的不确定性。
计算相邻时段负荷概率分布的Wasserstein距离,如图4所示。
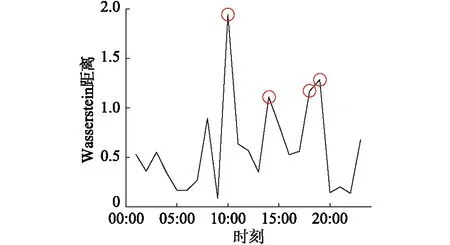
图4 24 h负荷概率分布的Wasserstein距离Fig.4 Wasserstein distance between 24 hours load probability distributions
图4中,10:00,14:00,18:00,19:00处的Wasserstein距离很大,表明在这些时段负荷水平的概率分布与上一时段发生了较大的变化,以此来表征用户用电行为的规律性变化,而随机性变化的影响通过概率分布的方式减弱了。
以相邻Wasserstein距离作为合并的依据,其定义为全部“质量”移动单位距离,即到相邻区间所做的“功”。全部“质量”概率分布之和为1,单位距离也为1,因此相邻Wasserstein距离为1。将距离小于相邻Wasserstein距离的时间段进行合并,大于相邻Wasserstein距离的时间段进行划分,图4中的圆圈处即为划分时刻。最终每日的负荷被划分为5个状态,用户状态划分结果如图5所示。

图5 负荷状态划分结果Fig.5 Result of load situations division
在不同的时间阶段,将负荷划分成不同的用电状态。在每一个用电状态中,为保证在这一时段任何时刻微网的供电能力均大于该负荷的电力需求,可以取每个状态的最大值作为微网形成决策的输入量,并设置一定的风险阈值来排除个别数据带来的影响,例如设置阈值为99%,即实际负荷高于决策提供负荷具有1%的风险。显然,相比于直接取负荷的额定功率作为输入量,上述方法可使微网随用户用电状态变化来进行调整,更具灵活性。
2 微网静态重构策略
将所有负荷划分成不同状态,这些状态的组合形成不同时刻的静态断面,将其作为本节模型的输入决策量。文中建模场景主要为含多个可控DG的辐射状配电网。系统配备远程控制开关等,使得开关动作可以完成,备用设备、恢复措施可以快速投入[16—17]。在极端灾害的场景下,将脱离主网的配电网划分为若干个微网,使得整个配电网恢复供电负荷的总价值最大。假设系统所有节点的集合为N,可控DG的集合为G。由于一个DG给一个微网供电,最终形成多个微网,因此微网的集合K与G相同。其中,某个微网由该微网的DG所在节点的编号表示,即若微网k的DG位于节点kg处,则k=kg。
2.1 目标函数
极端灾害发生时,恢复负荷的价值主要与负荷的重要程度以及功率有关,在关键负荷的量化评估方面[18—20]文中不再赘述。负荷的重要程度用负荷权重wi来表示,恢复负荷的功率大小由第一章负荷状态划分确定。恢复负荷的总价值可以用整个系统内所有负荷的负荷权重与恢复功率的乘积来表示,由于该值的单位与功率的单位相同,下文均称为“功率价值”。目标函数为:
(1)
式中:wi为节点i处负荷重要性权重;rik为节点供电状态,当节点被某一可控DG供电时,rik=1,否则rik=0;pi为节点i处负荷某状态下的最大功率需求。“功率价值”随时间的积分称为“电量价值”。
2.2 约束条件
2.2.1 节点微网关系约束
在模型中,每一个微网仅由一个可控DG供电,任意2个微网之间没有相同的节点,即:
(2)
式中:gik为节点微网关系,当节点i属于微网k时,gik=1,否则gik=0。同时,含有可控DG的节点kg必定属于自己供给的微网k,则有:
gkgk=1k∈K;kg=k
(3)
2.2.2 辐射状拓扑节点关系约束
若节点j为节点i的直接子节点,且节点j属于微网k,则节点i必然属于微网k。
gjk≤gikj∈C(i,k)
(4)
式中:C(i,k)为在微网k的辐射状拓扑中节点i的直接子节点。
2.2.3 线路开关状态约束
线路的开关状态与节点是否属于微网k存在如下约束关系:
(5)
(6)
其中,lij=1和lij=0分别表示节点i,j之间的线路闭合与断开。
2.2.4 节点负荷支撑约束
承压浆配方:基浆50m3(密度1.80g/cm3)+1.5%中酸溶性桥塞堵漏剂+1.5%细酸溶性桥塞堵漏剂+1%雷特随钻堵漏剂+果壳类材料,总浓度10%。
当节点i属于某一微网k,同时该节点的负荷连接微网的开关闭合时,节点i被微网k供电,即:
rik=giksi
(7)
式中:si为节点开关状态,当节点i处负荷连接到微网时,si=1,否则si=0。式(7)为非线性等式约束,考虑到3个变量均为0-1变量,可将其转化为式(8)的线性不等式约束。
(8)
2.2.5 微电网运行约束
微电网运行约束包括功率平衡约束、线路潮流约束、电压约束。潮流模型采用文献[21]中的配电网潮流模型,并将潮流线性近似形成约束条件[22]。
(1) 最大功率约束。
(9)
式中:Pi,k,Qi,k分别为在第k个微网中流入节点i的有功功率和无功功率;Pk,max,Qk,max分别为微网k的可控DG所能提供的最大有功功率和无功功率。
(2) 功率平衡约束。
(10)
(3) 线路潮流约束。
Pj,k≤Plijj∈C(i,k)
(11)
式中:Plij为线路lij的额定有功功率。
(4) 电压关系约束。
(12)
式中:Vi,k,Vj,k分别为节点i,j的电压;rij,xij分别为线路lij的电阻和电抗;V0,k为可控DG参考电压;oj,k为松弛变量,能使得当节点j与节点i不属于同一微网时上述约束仍有效,松弛变量约束为式(13)。
0≤oj,k≤(1-gjk)V0,k
(13)
同时,节点电压必须在线路额定电压容差的范围内,即:
VR(1-η)≤Vi,k≤VR(1+η)
(14)
式中:VR为线路额定电压;η为线路电压允许误差百分比。
2.3 求解方法
通过上述建模,将微网形成优化问题转化为一个混合整数线性规划问题。分支定界法是求解此类整数规划问题的常用方法,其主要流程如下:
(1) 求解松弛问题。先不考虑整数限制求解原问题,若求得最优解,检查是否符合整数约束,满足则为最优解,不满足则进入下一步。
(2) 分支。选择不符合整数约束的变量xj,其值为bj,构造2个约束x≤[bj],x≥[bj]+1 ,分别加入原问题中,形成2个子问题,[bj] 为小于bj的最大整数。
(3) 定界。检查子问题的解是否符合整数条件。将所有子问题中的目标函数最大值作为最优值z*的上界Uz,已经符合整数条件的分支中目标函数最大的作为下界LZ。
(4) 对于目标函数大于下界LZ的子问题,从目标函数最大的子问题开始,逐一分支,并更新问题的下界LZ。
(5) 当所有子问题的目标函数值都小于或等于LZ时,LZ对应的整数解则为最优解。
此方法可以利用Cplex求解器,方便快速求得在最大程度恢复负荷价值前提下的微网结构以及各微网所支撑的节点负荷。
3 微网动态重构寻优方法
求出每一个负荷断面的静态优化结果,就可获得全周期最佳运行状态。在无重构次数限制条件下,优化结果中需要重构的次数与负荷状态变化以及负荷水平有关,负荷水平较低,用电需求均能被满足,变化不大的时段优化结果往往无须重构。但实际上每天网络重构的次数是有限的,实际优化结果一般在7次以内。若优化结果为7次,则当重构次数限制为3时,最多有35 种情况;当重构限制次数为1或6时,有1种情况,因此可以采取枚举法。但当优化结果重构次数较多,最多23次(文中的状态是以1 h为基本单位,在这1 h中所有负荷的状态视为不变,全天24 h共有23个状态,因此最极端的状况是每小时之间都发生拓扑变化,最多23次),重构次数限制为11或12,此时产生的情况最多,有1 352 078种。对于此类情况,可以采用遗传算法[8]代替枚举法生成重构方案寻优。
4 算例分析
文中采用的IEEE 37节点系统[7]如图6所示,其中节点702、节点710、节点728含有可控DG。线路、负荷的恒开、恒闭状态可能由失去远程控制能力造成,也可以是其他强制性原因,例如某些节点不允许失负荷,因此可设置为恒闭负荷。

图6 IEEE 37节点系统Fig.6 IEEE 37-bus test system
各个节点的额定功率、权重以及节点状态信息可参考文献[7]。DG所在的节点及其最大功率如表1所示。

表1 DG基本信息Table 1 Basic information of DG
采用静态划分方法[7],利用节点的额定功率以及线路状况对微网进行建模,通过Cplex求解器求解,最终静态最优结果下的微网划分如图7所示。

图7 微网静态重构的优化结果Fig.7 The optimization result of microgrid static reconstruction
图7中,3块多边形区域为3个不同的微网,分别由3个可控DG供电。采用额定功率对微网进行静态划分的结果与文献[7]一致。
考虑负荷状态变化,根据第一章负荷状态划分方法,获得各时段下节点负荷的功率变化状况,在不考虑重构次数限制的条件下,微网的动态最优重构方式如图8所示。
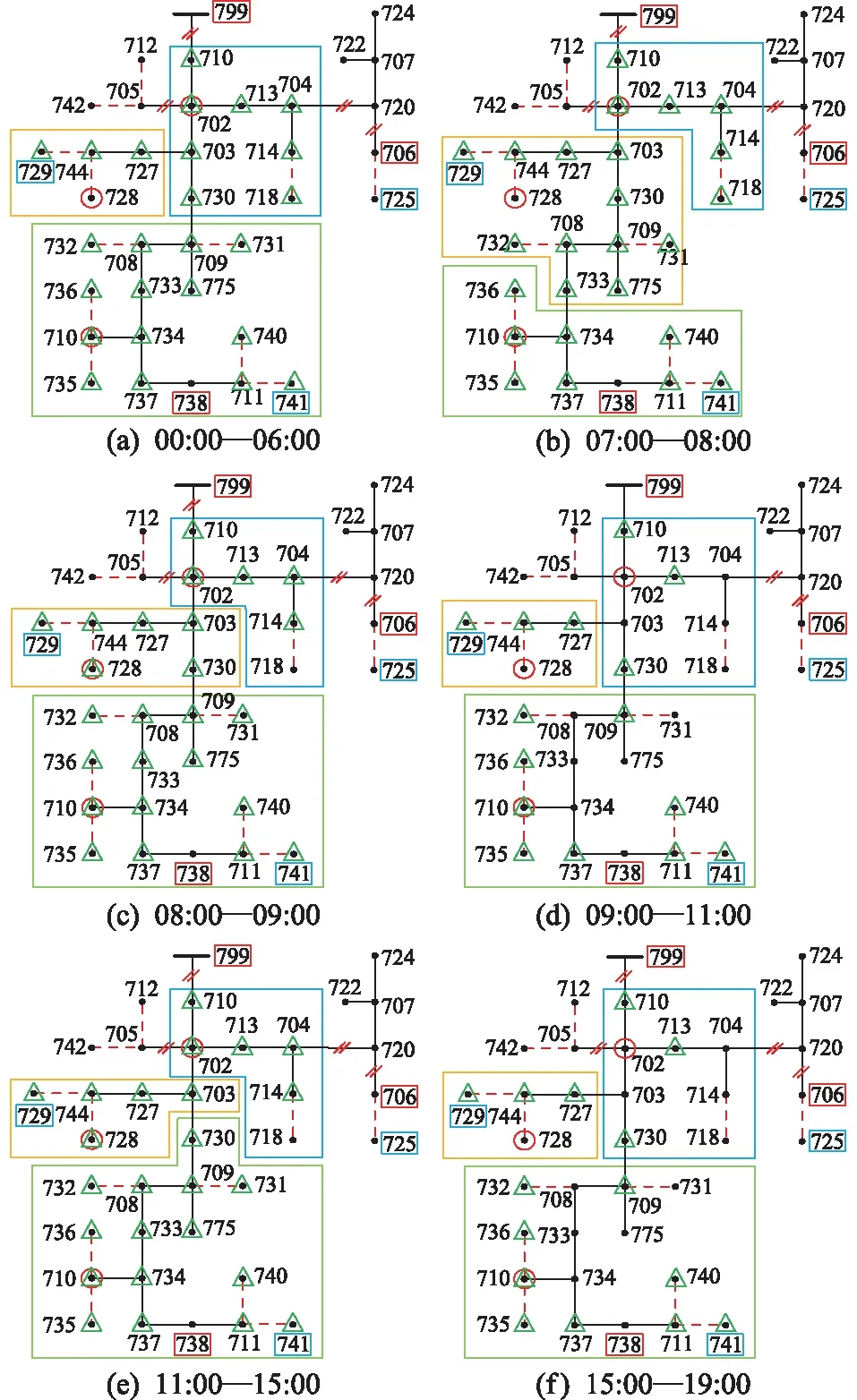
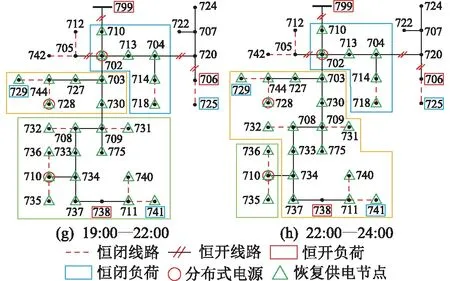
图8 不考虑重构次数限制的动态最优重构方案Fig.8 A dynamic optimal reconstruction scheme with-out considering the limit of reconstruction times
由图8可知,在不考虑微网重构次数的情况下,在07:00,08:00,09:00,11:00,15:00,19:00,22:00时刻重构微网结构,能在负荷变化的动态过程中使恢复供电负荷总价值最大。
考虑微网重构次数限制,设整日重构次数不超过3次,共有35种重构方案。枚举法具体操作方法为:将存在重构动作的7个时间点编号,利用Matlab中的组合函数,给出从7个时间点抽出3个的所有方案,并把所有抽到的方案输入到模型中,计算各方案全周期恢复的总电量价值,结果如图9所示。重构次数限制下动态重构方案的对比如表2所示。
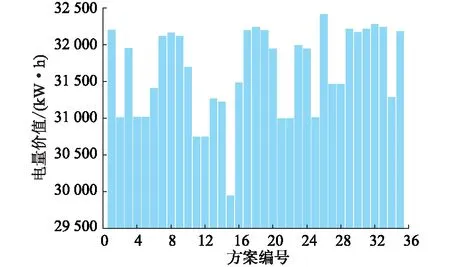
图9 重构次数限制下方案恢复总电量价值的比较Fig.9 Comparison of the total power recoveryvalue under the limit of reconstruction times
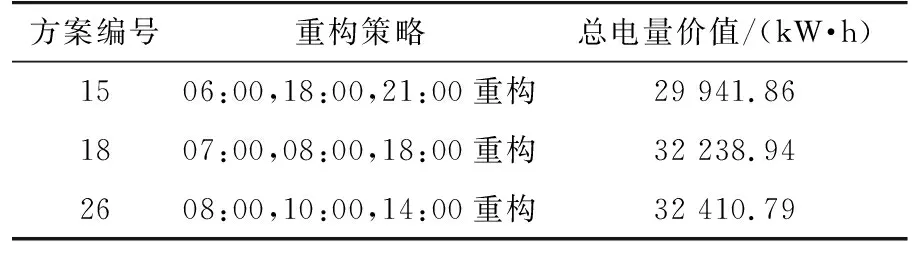
表2 不同动态重构方案对比Table 2 Comparison of different dynamic reconstruction schemes
由图9和表2可得,在考虑重构次数限制的条件下,方案26选择功率价值提升最大的时段重构,即在08:00,10:00,14:00这3个时刻对微网进行重构,总电量价值最大。
是否考虑重构次数的静、动态重构方案的恢复负荷总功率价值变化如图10所示。

图10 微网动态重构与静态重构过程对比Fig.10 Comparison of dynamic and static reconstruction of microgrid
由图10可知,静态重构的优化结果以负荷额定功率作为输入量,当实际负荷接近额定值时,静态重构与动态重构的结果相近,但随着负荷水平的降低,动态优化可以通过转移供电的方式支撑更多负荷,提升恢复的电量价值。计算图10中的功率价值曲线和时间轴包围的面积,获得3种情况下恢复的总电量价值,如表3所示。

表3 不同重构方法对比Table 3 Comparison of different reconstruction methods
不考虑重构次数的动态重构为理想状态,实际应用中需要根据重构次数限制,保留重构效果最好的方案26,其恢复总电量价值为32 410.79 kW·h。
5 结语
文中分析了负荷的概率分布特性,充分考虑了目标函数的特殊性以及决策的保守性,利用Wasserstein距离将负荷状态划分为不同的时段,作为微网划分策略优化模型的输入。同时,动态重构使得微网划分更加灵活,可在脱离主网的情况下最大化可控DG恢复负荷的总价值,从整体上提高配电网应对极端灾害的能力。目前,对配电网基础网架进行划分可以充分发挥联络线及柔性负荷的作用。文中主要从拓扑方面提升系统性能,而源荷储的优化调度对系统性能的提升也是值得深入研究的。
