多通道长短期记忆卷积网络的风速预测

修春波， 苏欢， 苏雪苗

(天津工业大学控制科学与工程学院，天津 300387)

0 引言

风能作为一种清洁、无污染的可再生能源得到了快速开发和应用，而大规模风电并网是风能利用最有效的途径之一。但风能具有明显的间歇性、波动性，因此风电具有较强的不确定性、随机性和不可控性[1—3]，风电会对电网产生较大的冲击，甚至影响电网的稳定运行。通过对风速进行有效预测，及时调整调度计划，能够有效减少电力系统备用容量，降低风电成本，改善电能质量[4—6]。因此，风速预测一直是风电领域的研究热点之一。

风速序列的预测方法较多[7—11]，主要分为基于数值气象预报的预测方法和基于历史数据的预测方法。前者根据实际的气象条件，如温湿度、风向、气压等数据，利用气象预报模型实现风速预测。而后者是从历史数据序列中提取蕴含的规律信息，由此实现对未来数据的预测。如持续预测法是早期的一种较实用有效的风速序列预测方法，但其预测机理过于简单，预测准确性较低。随着研究的深入，时间序列分析法[12]、神经网络法[13]、卡尔曼滤波法[14]、支持向量机(support vector machine,SVM)法[15]以及混沌理论[16]等都被应用于风速序列的预测分析中，改善了风速序列的预测性能。但这些方法均涉及到一个难以确定的关键参数，即被预测风速与历史输入数据的关联长度。历史关联数据过长会导致陈旧冗余的信息影响预测结果，而历史关联数据过短则会导致信息丢失或不足，同样会降低预测性能。在实际应用中，通常采用经验法或根据相空间重构理论进行构造，但对于混沌特性不明显的风速序列，样本的构造方式缺少相应的理论指导，预测性能不稳定。

近年来，深度学习理论发展迅速，在时间序列预测分析领域中表现出优异的应用性能[17—18]。例如，基于深度学习的循环神经网络(recurrent neural network，RNN)可应用于时间序列预测分析的求解中[19—20]，但该网络存在梯度消散和梯度爆炸等问题。为此，可采用长短期记忆(long short-term me-mory，LSTM)网络模型[21]实现时间序列的预测分析。LSTM网络结构独特，是RNN的改进网络，对时间序列预测分析问题具有很好的求解性能[22—25]。尽管深度学习网络能够利用大数据样本获取时间序列中的规律信息，但预测数据关联长度等参数仍须人为选定，这限制了深度学习网络在风速序列预测中的应用性能。

为了避免不恰当的关联数据长度等影响网络预测性能，提出一种多通道LSTM网络与一维卷积神经网络相结合的风速序列预测方法。该方法通过构建多通道LSTM子网络获得与不同输入数据长度相关的风速序列计算值，对各LSTM子网络的输出值进行一维卷积操作，并利用全连接网络层输出预测值。同时，为了避免预测过程中可能出现的误差累积及漂移，对预测值进行误差补偿修正，进一步提高预测精度，改善风速预测性能。

1 LSTM网络模型

通常，实际时间序列中各个数据点之间具有时间上的顺序关联性。采用传统的前向型神经网络进行时间序列预测分析时，时间序列中数据点之间的顺序关联性只能体现在构建的训练样本中，而网络自身结构中不具有体现数据点时间顺序关联性的机制。相比而言，RNN利用隐藏层节点之间的连接，能够很好地描述时间序列中数据之间的顺序关联性，从结构上更符合时间序列预测要求。但RNN对序列信息的利用缺少选择性，当序列长度过长时会出现梯度消散的问题，因此，RNN不适合用于复杂时间序列的预测分析。

LSTM网络模型是一种改进的RNN模型，解决了梯度消散问题，利用门结构实现了对序列信息的选择性利用，适合复杂时间序列预测问题的求解。LSTM网络模型的基本单元如图1所示。

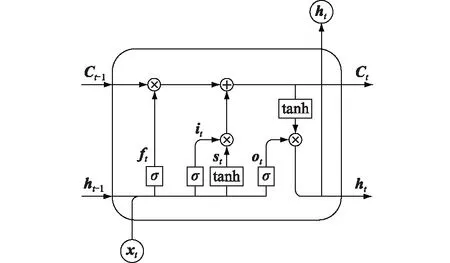
图1 LSTM网络模型的基本单元Fig.1 Basic unit of LSTM network model

图中，ft，it，ot分别为遗忘门、输入门和输出门的状态；st为输入节点状态；ht，ht-1分别为当前时刻和前一时刻的输出；xt为当前序列的输入；Ct，Ct-1分别为当前时刻和前一时刻记忆单元的状态信息。LSTM网络的基本单元中包含了门结构和记忆单元，利用遗忘门、输入门、输出门可实现记忆单元信息的添加或删除。LSTM网络基本单元的输入包含xt，Ct-1以及ht-1。在遗忘门中，xt和ht-1共同决定Ct-1的遗忘部分。在输入门中，xt，ht-1经过Sigmoid和tanh函数变换后共同决定当前记忆单元状态信息的更新部分。通过遗忘门和输入门，将Ct-1更新为Ct。在输出门中，xt和ht-1经过Sigmoid函数变换得到ot，Ct经过tanh函数变换后和ot共同组成ht。该单元的具体计算过程如下：

ft=σ(Wf·[ht-1,xt]+bf)

(1)

it=σ(Wi·[ht-1,xt]+bi)

(2)

st=tanh(Ws·[ht-1,xt]+bs)

(3)

Ct=ft∘Ct-1+it∘st

(4)

ot=σ(Wo·[ht-1,xt]+bo)

(5)

ht=ot∘tanh(Ct)

(6)

其中，[ht-1,xt]表示将ht-1和xt这2个列向量拼接成1个列向量，即：

(7)

Wf，bf分别为遗忘门的权重系数矩阵和偏置项；Wi，bi分别为输入门的权重系数矩阵和偏置项；Ws，bs分别为输入节点的权重系数矩阵和偏置项；Wo，bo分别为输出门的权重系数矩阵和偏置项；σ(·)和tanh(·)分别为Sigmoid函数和双曲正切函数。式(4)和式(6)中“∘”表示按元素乘运算。

遗忘门和输入门是LSTM网络基本单元的核心结构，能够使网络更有效地保持长期记忆。一般来说，网络输入数量的多少表明了网络输出值与历史数据的关联长度。由于风电场风速序列的形成机理复杂，未来风速值与历史数据的关联长度难以人为有效确定，即网络的输入数据数量不容易有效确定，输入数据量较少时会造成信息丢失，输入数据较多时会造成信息冗余，均会降低模型的预测性能。为此，文中针对风速序列预测问题，结合卷积网络结构，构建对输入数据量具有一定适应性的多通道LSTM网络预测模型，实现预测特征信息的有效提取。

2 多通道LSTM网络预测模型

2.1 网络结构

作为一种气象数据，风速时间序列通常短期可预测、长期难以预测，且预测值与历史数据的关联长度也很难利用先验知识进行选取。为提高预测模型的有效性，构建多个具有不同输入长度的LSTM子网络，并利用卷积网络将各子网络的输出进行结合，从而构成多通道LSTM网络预测模型。例如，对预测步长为n的风速序列预测问题，多通道LSTM预测网络与卷积网络(multi-channel LSTM and convolution neural net-work，MCLSTM-CNN)相结合的预测模型结构如图2所示。

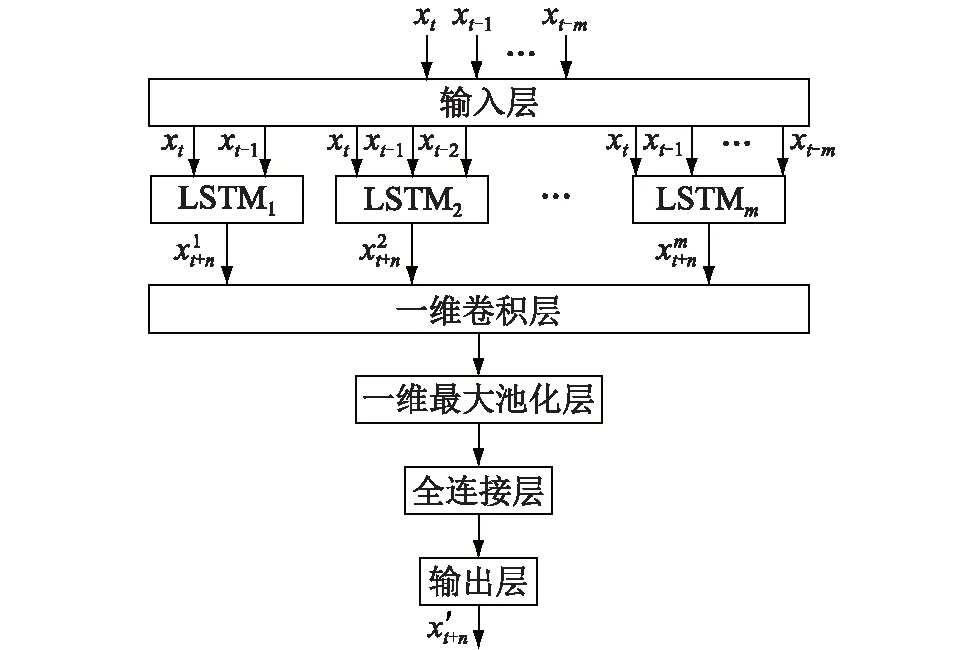
图2 MCLSTM-CNN网络模型Fig.2 MCLSTM-CNN network model

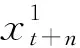
将网络第一部分中m个LSTM子网络输出的风速预测值构成一维信号，作为一维卷积神经网络的输入，卷积网络中卷积操作的卷积核大小为2，最大池化操作的池化窗口大小为2。使用卷积网络对一维信号进行特征提取，最后通过全连接层输出最终的风速预测值x′t+n。

一维卷积神经网络是一种用于处理时序数据等一维信号的特殊神经网络，由卷积层、池化层和全连接层组成。卷积层利用权值共享和不同尺度的卷积核可以实现网络所需特征的自动提取。池化层则从卷积层中提取到主要的特征，并在时间维度上进行降维操作，减小数据计算量。全连接层对全局特征进一步抽象组合，得到最终输出预测值。

上述预测模型利用卷积层实现了预测信息的自动提取，避免了单一LSTM网络输入数据量等参数须人为选取的问题。当模型输入历史数据长度足够，即m值足够大时，模型就能够利用历史数据构成的训练样本自动实现网络参数的调整，并确定各子网络的预测权重，从而有效提高网络的泛化能力，改善网络的预测性能。

2.2 误差补偿法

随着预测过程的进行，误差累积及漂移不可避免，为此，对网络预测结果进行动态误差补偿来进一步减小预测误差。

对于预测步长为n的风速序列预测问题，利用MCLSTM-CNN模型连续预测可得到各个时刻的预测值，设t-n时刻，t时刻，t+n时刻的预测值分别为x′t-n，x′t，x′t+n，则对x′t+n进行动态预测误差补偿，得到最终的预测结果x″t+n为：

x″t+n=x′t+n+γ(t)e(t)

(8)

式中：e(t)=xt-x′t，为t时刻的网络预测误差；γ(t)为动态补偿系数，其值根据补偿结果误差的负梯度方向进行调整，即满足式(9)—式(11)。

(9)

E(t)=(x″t-xt)2

(10)

x″t=x′t+γ(t-n)e(t-n)

(11)

式中：η为动态调整步长；E(t)为步长结果误差；x″t为t时刻序列点的最终预测结果。

根据历史预测误差漂移情况，对第n步预测结果进行动态误差补偿，能够在一定程度上有效克服连续预测过程中出现的误差累积漂移问题，从而进一步提高风速序列预测的有效性。

3 风速预测仿真实验与结果分析

3.1 数据集与预处理

选取某风电场检测的风速数据进行预测分析，风速数据的采样间距为15 min,以时间先后为序构成风速数据集。该风速数据集的最大风速为18.72 m/s，最小风速为0.91 m/s。将数据集中前90%的数据作为训练样本，用于网络模型的训练，后10%的数据作为测试样本，用于测试网络模型的预测性能。

采用min-max方法对数据进行归一化处理，将风速数据的数值映射到[0，1]内，归一化计算方式为：

(12)

式中：xi为第i个数据归一化后的数值；yi为第i个数据归一化前的数值；ymax为数据集中的最大值；ymin为数据集中的最小值。

采用3种评价指标评价模型的预测性能，分别为均方根误差(root mean square error，RMSE)，平均绝对误差(mean absolute error，MAE)，平均绝对百分比误差(mean absolute percentage error，MAPE)，其计算如下：

(13)

(14)

(15)

式中：N为预测数据总个数；y″i为第i个数据的预测值。

3.2 实验结果与分析

分别采用具有预测误差补偿(error com-pen-sation，EC)的MCLSTM-CNN预测模型(MCLSTM-CNN-EC)、SVM、反向传播神经网络(back pro-pa-ga-tion neural network,BPNN)、LSTM[23]、卷积循环神经网络[20](convolutional recurrent neural network,CRNN)、MCLSTM预测模型以及未进行误差补偿的MCLSTM-CNN预测模型对风速序列进行超短期预测分析对比实验。其中，CRNN模型采用一维卷积神经网络先对输入风速序列进行特征提取，再利用LSTM网络对风速值进行预测输出。MCLSTM模型采用文中所提出的多通道LSTM子网络直接与全连接层相结合，即省去了卷积层与池化层。

设预测步长n为16，即对4 h后的风速值进行预测分析。选取历史输入序列长度为10，即上述各预测模型的输入层神经元个数均为10，输出层神经元个数均为1。预测模型的训练批次大小为32，训练迭代次数为300次，将归一化后数据的均方误差作为损失函数，优化算法为Adam算法。

MCLSTM-CNN模型训练过程中损失函数值随迭代次数的变化如图3所示。

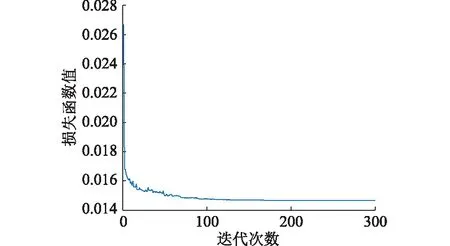
图3 MCLSTM-CNN在数据集上训练时的损失函数Fig.3 Loss function of MCLSTM-CNN on dataset

由图3可见，预测网络能在300次迭代内完成参数训练。图4为上述各预测模型的预测结果。图5为图4的局部预测结果(前150个预测数据)。

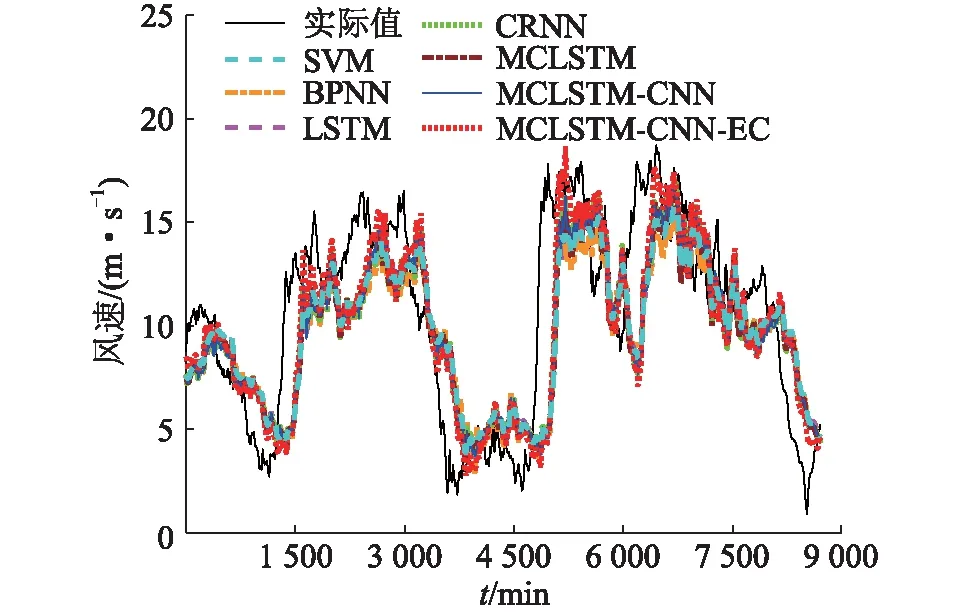
图4 各预测模型的预测结果Fig.4 Prediction results of each prediction model

由上述预测结果可见，虽然各种预测方法相对于实测数据均出现了一定的滞后现象，但MCLSTM-CNN-EC的预测曲线与实测数据具有更好的拟合度，表现出更好的预测性能。

表1和表2分别为图4与图5所示预测结果的误差评价指标。

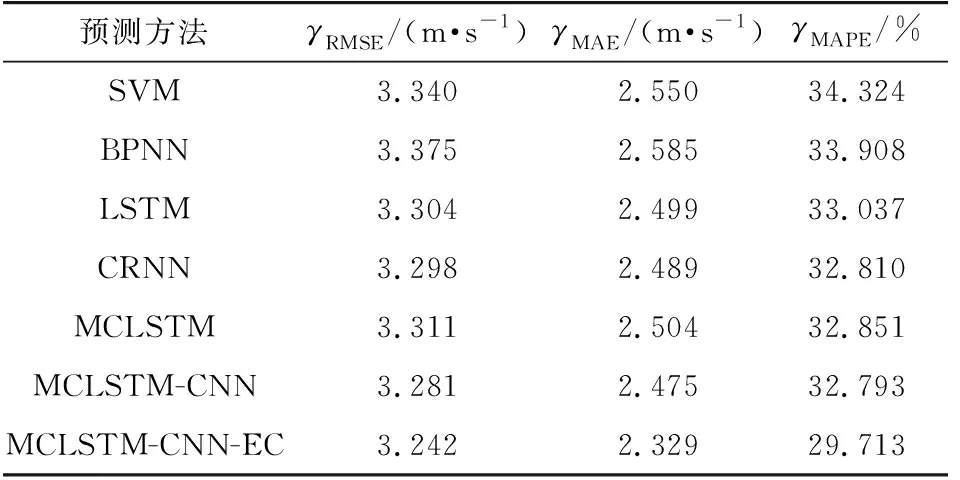
表1 数据集的预测误差指标Table 1 Prediction errors of dataset

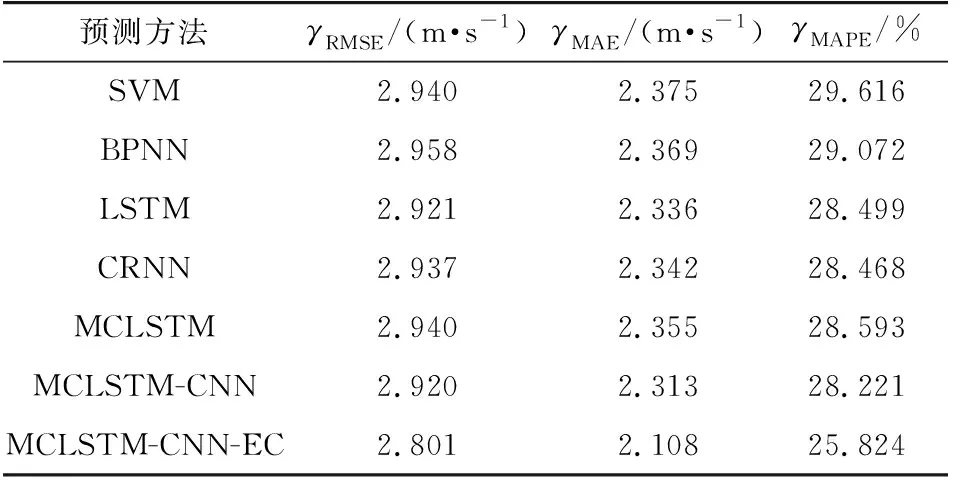
表2 数据集前150个预测数据的预测误差指标Table 2 Prediction errors of the first 150 prediction results of dataset

由上述预测结果以及预测评价指标可知，基于深度学习的LSTM网络和CRNN模型的预测性能优于传统BPNN和SVM模型，说明基于深度学习的预测网络对历史数据信息具有更强的预测特征提取能力，可有效提高风速序列的预测精度。而CRNN模型利用卷积神经网络提取风速序列的深度特征信息，以此为基础利用LSTM模型进行预测，与单一的LSTM网络相比，CRNN模型具有更好的预测性能。MCLSTM-CNN模型利用多通道LSTM子网络结构实现不同关联数据长度信息的提取，可有效提高模型对预测序列的适应性，根据子网络的输出，利用卷积层自动提取预测信息，能够从历史数据中获得适合序列预测的特征参数，避免了输入数据长度参数难以选取的问题，因此，预测结果相比于LSTM、CRNN等预测模型更优。同时，MCLSTM-CNN模型在各项误差指标上也优于缺少卷积层和池化层的MCLSTM模型。可见，MCLSTM-CNN模型中的一维卷积神经网络能更好地提取多通道LSTM子网络的特征信息，说明了MCLSTM-CNN模型结构的合理性。在此基础上，MCLSTM-CNN-EC方法对MCLSTM-CNN模型输出的预测值进行动态误差补偿，克服了预测过程中产生的误差累积与漂移，因此其各项预测误差指标明显降低，预测性能得到了进一步改进。在上述的各种网络模型中，MCLSTM-CNN-EC模型具有最优的预测性能和良好的泛化能力，可有效提升风速的超短期预测精度。

4 结语

针对风速序列超短期预测问题，提出了多通道LSTM子网络与一维卷积神经网络相结合的预测模型。利用多个LSTM子网络实现基于不同历史数据长度的风速序列预测计算，采用一维卷积网络对各子网络的计算结果进行特征信息的自动提取，得到网络的预测值，利用动态误差补偿方法对网络预测值进行校正，能够有效克服预测过程中所产生的误差累积与漂移。该方法在风速序列超短期预测中表现出良好的预测性能，实验对比结果验证了该网络结构的合理性。文中方法研究了基于历史数据信息的风速预测方法，为进一步提升风速预测有效性，未来可开展结合数值气象预报信息的深度学习风速预测方法研究，从而提升风电并网的性能。