考虑地层应变软化的盾构下穿密集建筑物沉降分析

2022-02-12黄兴贾少东姚超凡何有成马杲宇王士民徐一帆

铁道建筑 2022年1期

黄兴贾少东姚超凡何有成马杲宇王士民徐一帆

1.西南交通大学交通隧道工程教育部重点实验室，成都 610031；2.南宁轨道交通集团有限责任公司，南宁 530029

盾构施工中地表变形的预测、监测、控制是盾构法城市地铁隧道施工和研究的重点。早期的地表变形研究以1969年Peck［1］提出的地表沉降估算公式为代表。此后，基于圆孔扩张理论建立的地层位移解析解被广泛使用［2］。近年来，围绕盾构施工地表变形问题，国内学者展开大量研究。

在地表变形的预测方面，郑刚等［3］考虑土体小应变硬化特性，建立预测隧道变形的有限元模型并对地表位移特征进行分析。刘旭东［4］将摩尔-库伦本构模型（MC）、硬化土本构模型（HS）和小应变硬化土本构模型（HSS）的沉降模拟结果与过江隧道现场监测数据进行对比，证明HSS本构模型预测结果最优。郭社军等［5］对小半径曲线隧道地层损失的影响因素进行分析，并对Peck公式进行修正。在地表变形的监测方面，陈庆章等［6］对富水砂性地层盾构施工参数进行优化。郭建宁［7］、尚艳亮［8］系统研究了无水砂层的地层沉降特性，提出相应优化措施并建立预警机制。在地层变形的控制技术方面，李士中［9］研究了不同地层加固范围和加固方案对应的盾构下穿既有铁路引起的路基变形规律。刘学彦等［10］对盾构侧穿、正穿建筑物时的地表沉降特性进行分析，并优化了软弱地层的盾构施工参数。何力超、陈传平等［11-12］研究了盾构下穿密集建筑群的沉降规律，并建议通过优化施工方法减小地层变形。

本文以南宁市轨道交通5号线五一立交站—新秀公园站隧道工程为背景，考虑砂质地层应变软化效应，采用数值模拟分析盾构下穿密集建筑物区的地表变形及建筑物不均匀沉降规律，以掌握盾构连续下穿密集建筑物互馈机制。

1 工程概况

五一立交站—新秀公园站区间隧道采用土压平衡和泥水平衡双模式盾构施工，全长约2101.09 m。邕江南岸地质纵断面如图1所示。盾构于邕江南岸采用泥水平衡模式始发，随即下穿密集建筑物区，而后换为土压平衡模式进入越江段施工。隧道开挖直径为6.3 m，内径为5.3 m，衬砌为预制钢筋混凝土管片，混凝土强度等级为C50。隧道穿越的地层主要为第四系和古近系地层，其中邕江南段施工地层多为粉土-粉细砂、粉细砂-圆砾、粉土-圆砾、圆砾-泥岩等复合地层。

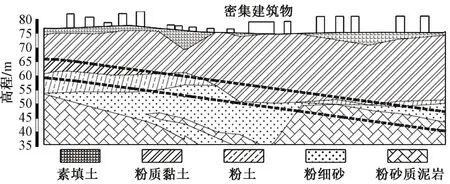
图1 邕江南岸地质纵断面（单位：m）

2 数值模型

2.1 地层应变软化本构模型

针对砂质地层的数值模拟，采用应变软化本构模型的计算结果较理想弹塑性本构模型计算出的结果更大［13］，与实测地层变形结果更加吻合。采用考虑应变软化的摩尔-库伦本构模型，该本构模型常在断层错动数值仿真中使用［14］。土体受扰动后，应变软化特性主要表现为内摩擦角和膨胀角随剪切应变发生变化，计算公式［15］为

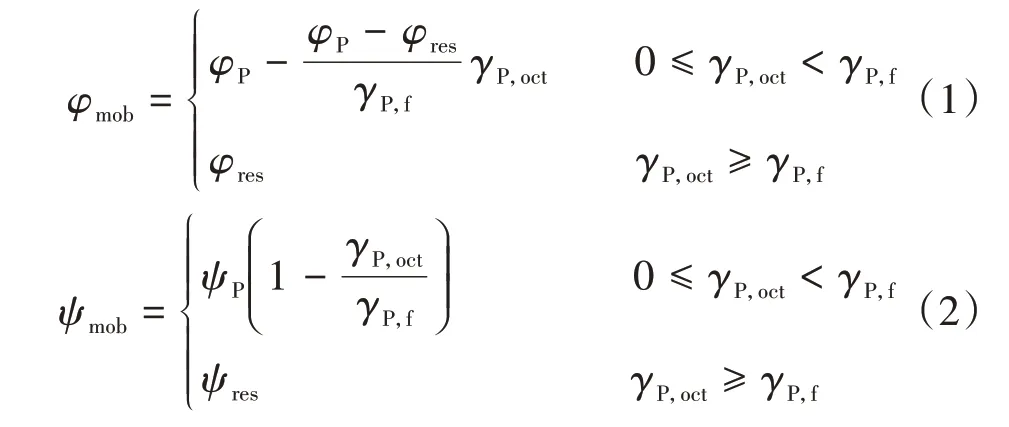
式中：φ为摩擦角，ψ为剪胀角，角标mob、P、res分别代表实时值、峰值、残余值；γP，oct为塑性八面体剪切应变；γP，f为软化阶段结束时的剪切应变值。

由上述计算式可知，砂质土达到峰值强度后，因材料性质发生劣化而进入软化区。该过程中土体的摩擦角φ、剪胀角ψ均会随塑性应变的增加而逐渐线性衰减；当土体剪切应变超过γP，f后便认为残余强度为一定值，不再发生改变。该过程也可用图2进行描述。模拟计算时，基础本构模型仍选用摩尔-库伦本构模型，利用ABAQUS内置的VUMAT用户子程序模块，通过编写自定义程序及时修改场变量以动态调整砂质土峰后强度，实现对砂质土应变软化特性的模拟。

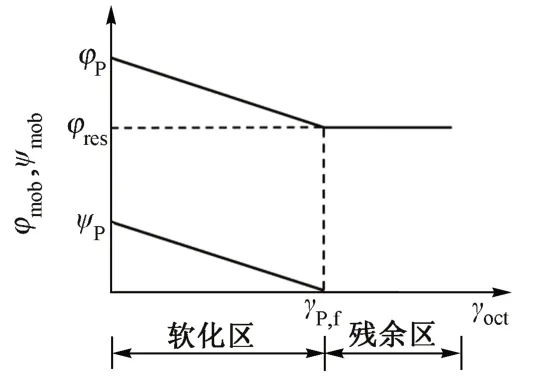
图2 应变软化模型

2.2 计算模型的建立

施工现场监测数据表明，隧道浅埋段的地层变形较为严重，地表老旧建筑物对地层变形十分敏感。选取隧道埋深10 m处的断面进行计算分析，该处隧道断面整体处于砂质地层中。利用ABAQUS建立如图3所示的模型。模型各部分材料参数见表1。土体黏聚力为1.0 kPa，峰值摩擦角为20°，残余摩擦角为15°。

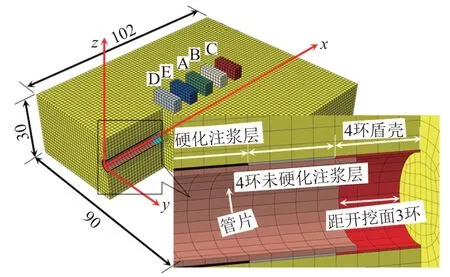
图3 计算模型（单位：m）

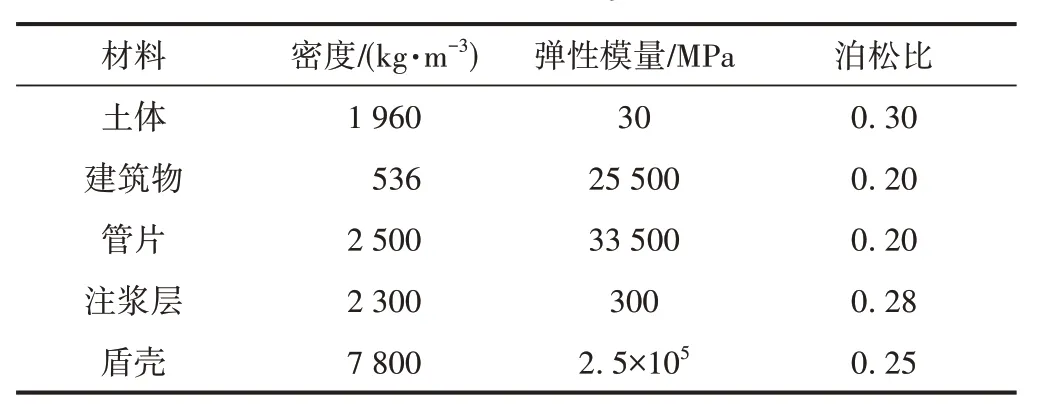
表1 模型材料参数

区间隧道采用的管片幅宽1.5 m，外径6.0 m，厚0.35 m。双模式盾构机盾壳纵向长6 m，厚0.15 m。施工时与地层之间会产生15 cm的盾尾间隙，该间隙通过同步注浆进行填充，计算时采用注浆等代层进行模拟。浆液硬化前的弹性模量取为硬化后的20%。

模型尺寸设为90 m×102 m×30 m，模型前后表面施加纵向约束，左右侧面施加横向约束，底面施加横向、纵向、竖向约束，上表面为自由面。模型单元类型均为C3D8R六面体减缩积分实体单元，单元尺寸约为1.5 m×1.5 m×1.5 m。注浆层与周围地层之间、建筑物与地层表面、盾壳与地层间的相互作用采用摩擦接触模拟，摩擦因数设定为0.9的地层残余摩擦角正切值；注浆层与管片间的相互作用采用tie约束进行模拟。

计算时首先在建筑物的作用下进行地应力平衡，而后利用model⁃change功能模拟盾构逐环开挖施工过程：①杀死第1环开挖范围内的土体单元；②激活该位置处的盾壳单元；③在开挖面上施加80%的开挖面不平衡力以模拟盾构机对开挖面土体的支撑作用；④鉴于盾壳纵向长度为6 m（4环管片长度），管片激活滞后开挖面3环，盾壳内保留1环管片、注浆层单元激活滞后开挖面4环、注浆层硬化处理滞后开挖面8环，注浆未硬化段为4环。以此类推直至开挖结束。

2.3 计算模型的验证

2.3.1 与现场实测数据对比

在不考虑建筑物的影响时，利用摩尔-库伦本构模型及应变软化本构模型计算出的自由场地地表横断面沉降如图4所示。可知：两种本构模型计算出的地表沉降变形规律基本一致，盾构施工造成的地层扰动范围集中在隧道中心线两侧18 m，约为3D（D为隧道开挖直径），该范围内地表沉降值从1 mm快速增长至最大沉降值；两种本构模型计算出的地表最大沉降数值存在明显差异，摩尔-库伦本构模型计算出的最大沉降为14.76 mm，应变软化本构模型计算出的最大沉降为17.21 mm，增幅16.6%；在隧道中线两侧12 m（约2D）的范围内，应变软化本构模型计算出的地表沉降明显大于摩尔-库伦本构模型，越靠近隧道中线两种本构模型的计算结果差异性越强。这表明，地层扰动较剧烈时，砂质土的应变软化特性十分明显，因砂质土峰后强度降低引起的地表沉降增量不容忽视。从现场监测数据来看，应变软化本构模型计算出的地表沉降曲线比摩尔-库伦本构模型更符合实际监测结果。说明针对砂质地层，在预测盾构施工引起的地层变形时，考虑应变软化特性是必要的。

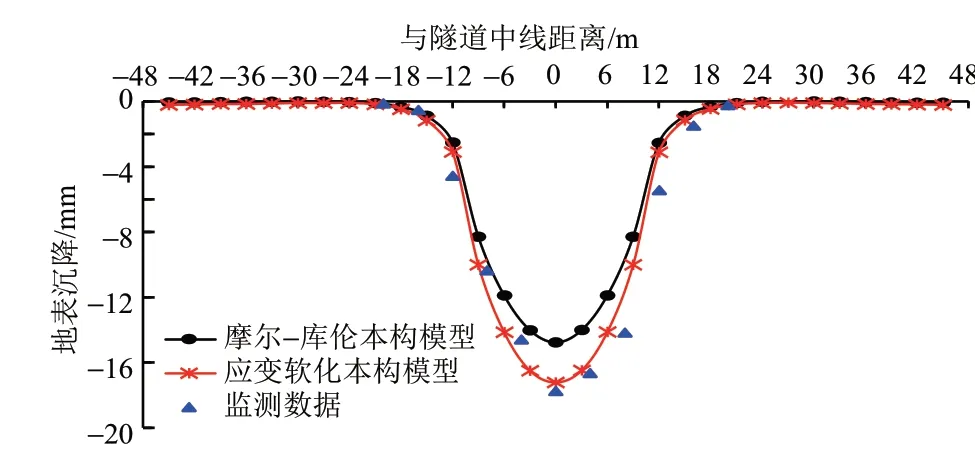
图4 自由场地地表横断面沉降

选取地表中心点（x，y，z）=（51，45，15）为监测点，得到自由场地地表沉降在盾构施工过程中的变化规律如图5所示。可知：①两种本构模型计算得到的地表沉降均表现为三段式沉降特性，第一部分为开挖面位于监测点前方24 m（约为4D）及以上时，盾构施工造成监测点处仅有少部分地层扰动，监测点处于轻微变形阶段，地表有微微的隆起或沉降产生；第二部分为开挖面位于监测点±24 m范围内，掌子面周围土体扰动区对监测点有强烈影响，监测点处于急剧变形阶段，当开挖面位于监测点正下方时，地表沉降速率达到最大，此时已产生的变形约占最终沉降量的65%；第三部分为残余变形，该阶段产生的沉降约占最终沉降量的3%，基本可忽略不计。②当开挖面位于监测点前方9 m（约1.5D）时，应变软化与摩尔-库伦本构模型的结果差异性开始凸显。两种本构模型的计算结果差值从0.39 mm增至2.46 mm，因砂质土应变软化特性引起的沉降占最终沉降量的14.3%。这表明，砂质地层受到较强扰动时应变软化特性明显，地层变形的发展较摩尔-库伦本构模型更快。同监测数据相比，应变软化本构模型更能揭示砂质地层的变形规律。

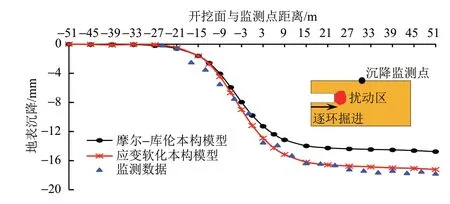
图5 掘进过程中自由场地地表沉降

2.3.2 与Peck公式对比

盾构施工引起的地表沉降一般采用Peck公式进行预测，其表达式［1］为

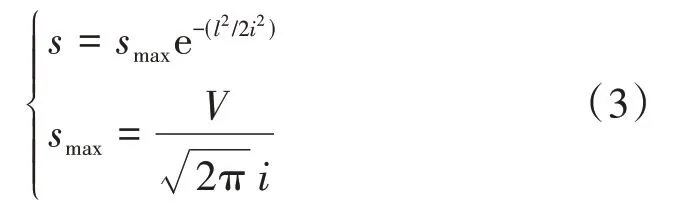
式中：s为任意点地表的沉降值，mm；smax为沉降曲线对称中心处的沉降值，mm；i为沉降槽的宽度，m，应结合具体地层条件确定；l为沉降计算点到对称中心的距离，m；V为单位长度地层损失率，m3/m，与施工方法等有关。

综合考虑现场监测统计数据及以往类似工程经验，确定该隧道区间开阔地段的沉降槽宽度i≈7.5 m，单位长度地层损失V≈0.34 m3/m，地层损失率约为1.2%，最大沉降量smax≈18 mm。Peck公式预测结果与应变软化本构模型计算结果的对比见图6。可知，地表沉降影响区域都集中在隧道中线两侧约3D范围内（-18～18 m），二者计算结果极差为1.58 mm，应变软化本构模型的计算结果与Peck公式预测结果基本吻合，地表横向沉降表征出明显的高斯函数分布规律。

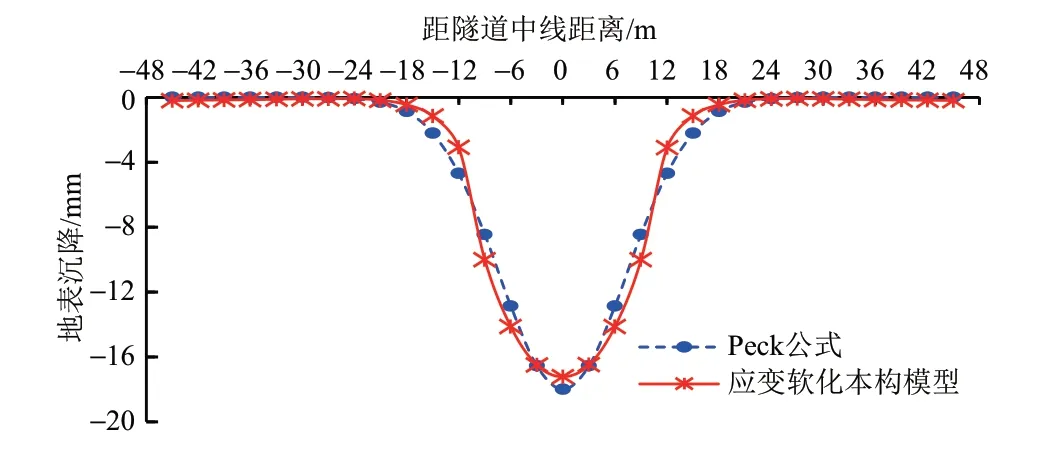
图6 地表沉降Peck公式预测结果与应变软化本构模型计算结果

综上，考虑应变软化的摩尔-库伦本构模型能更好地反映砂质地层的变形特性，表明应变软化本构模型在砂质地层地表沉降预测中的适应性。因此采用应变软化本构模型对砂质地层进行模拟，在此基础上探究建筑物分布形式及两建筑物间的净距对地层变形的影响规律，得出盾构施工连续下穿密集建筑物的地表变形特性及建筑物不均匀沉降规律。

3 地表变形规律

根据该区间隧道的实际下穿情况，选取典型建筑物尺寸为12.0 m×4.0 m×5.6 m（普通2层平房），建筑物荷载按每层15 kPa等效为均布面荷载施加在模型选定位置。如图7（a）所示，取两建筑物间的净距为5 m，依次考虑自由场地、建筑物A、建筑物AB、建筑物ABC、建筑物ABCDE五种计算工况（依次为工况1—工况5），探究不同建筑物分布形式对地表沉降及建筑物不均匀沉降的影响。如图7（b）所示，在仅有建筑物A、B的情况下，保持建筑物A的位置不变，通过改变建筑物B的位置，使两建筑物间的净距SAB依次为2.5、5.0、7.5、10.0 m，探究不同建筑物净距对地表沉降变形及建筑物倾斜的影响规律。图7中的横向中线及纵向中线为地表沉降的监测线。

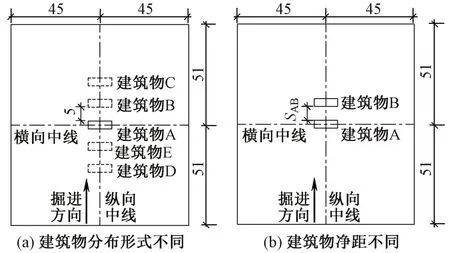
图7 计算工况选取图示（单位：m）

3.1 建筑物分布形式对地表变形的影响

盾构下穿不同分布形式建筑物时，地表变形曲线见图8。可知：①仅有建筑物A时地表横向最大沉降为18.72 mm，较工况1增加1.5 mm，增幅为8.7%；在建筑物A两侧增加建筑物，地表横向沉降增加，工况5对应的地表横向沉降最大，为-20 mm。这表明地面建筑物超载会使地表横向、纵向变形增大。②地表纵向变形表现出显著的多峰性，每个建筑物所引起的地表变形呈正态分布，且不同建筑物引起的沉降槽相互叠加，导致纵向地表变形影响区域改变。③建筑物净距为5 m时，每添加一处建筑物将导致相邻两建筑物处地表沉降增加约0.5 mm。④工况3与工况4对应的地表纵向沉降曲线在建筑物A附近基本重合，建筑物A处的地表沉降分别为19.37、19.38 mm，建筑物C对建筑物A处的地表沉降影响甚微。这表明地表沉降的叠加效应与距离有关。本研究中，建筑物引起的距其14 m之外的场地地表附加沉降增量可忽略不计。

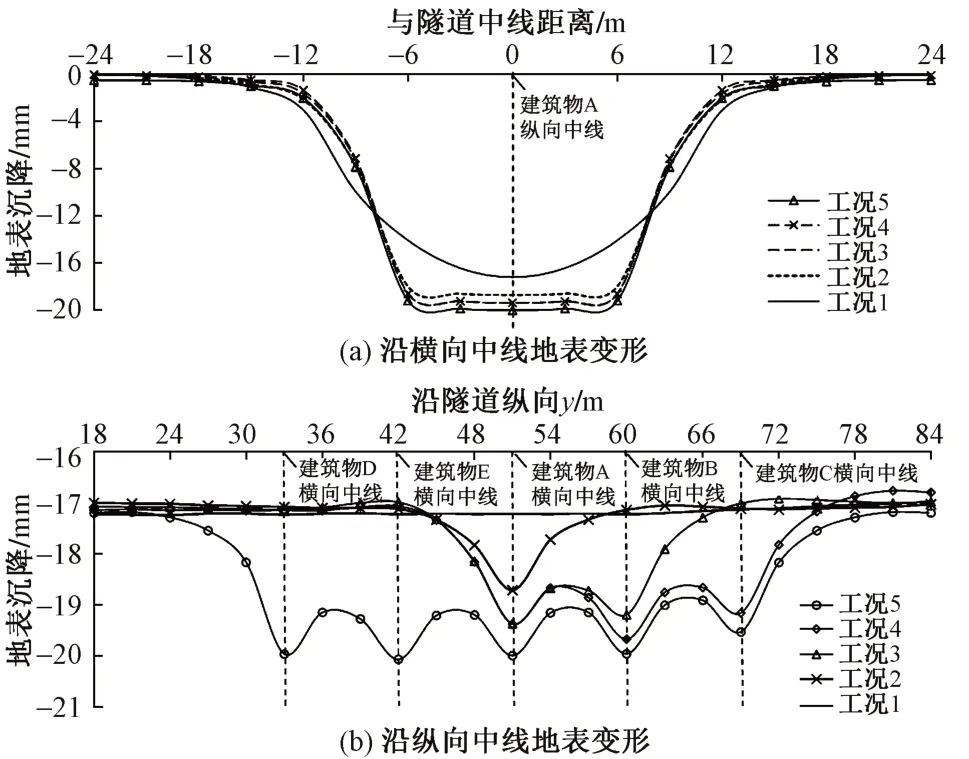
图8 盾构下穿不同分布形式建筑物时地表变形曲线

3.2 相邻建筑物净距对地表变形的影响

改变建筑物A、B间净距SAB得到盾构下穿不同净距建筑物的地表横向变形（图9）和纵向变形（图10）。由图9可知：地表横向变形影响范围与建筑物间的净距关系不大，地表横向变形仍集中在隧道中线两侧3D范围内；SAB对建筑物A处的地表沉降变形影响显著，随着净距增加，建筑物A处的沉降值明显减小。这验证了净距越小，建筑物间的相互影响越大的变形特征。由图10可知：地表纵向沉降影响范围及沉降变形大小与SAB关系密切，净距越小建筑物A、B之间的地表沉降值越大；地表纵向变形曲线呈非对称的W形，建筑物B处的地表沉降均小于相应工况建筑物A处的地表沉降。主要原因是：施工至建筑物A时，由于建筑物A、B间的衬砌结构尚未施工，建筑物A受前方建筑物B超载作用影响较大，地层沉降变形加剧；盾构施工至建筑物B时，后方建筑物A超载对建筑物B的影响由于衬砌结构的存在而削弱，建筑物B处受到建筑物A超载的影响相对较小。

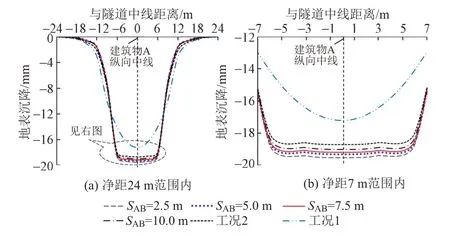
图9 盾构下穿不同净距建筑物时沿横向中线地表变形曲线

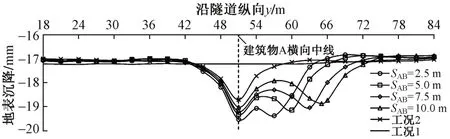
图10 盾构下穿不同净距建筑物时沿纵向中线地表变形曲线

4 建筑物不均匀沉降规律

4.1 建筑物分布形式对建筑物不均匀沉降的影响

将盾构掘进先达到建筑物A的一侧定义为前侧，另一侧定义为后侧。建筑物A前后两侧的沉降变形在盾构施工过程中的变化曲线见图11，前后两侧的沉降差值反映建筑物A的不均匀沉降大小。可知，工况2—工况5下盾构施工中建筑物A前后两侧沉降发展速率存在差异，盾构掘进至建筑物A正下方时不均匀沉降达到最大，依次为2.75、2.73、2.76、3.03 mm，工况5的不均匀沉降较其余工况增加约11%，可见建筑物A前侧存在建筑物超载对其施工中的不均匀沉降影响较大。由于建筑物A的不均匀沉降是由前侧受到地层扰动先产生沉降，而后侧沉降变形相对滞后造成的，随着盾构施工的推进建筑物A前后两侧的不均匀沉降值逐渐减小并趋于平稳，施工完成时不均匀沉降明显小于施工中的不均匀沉降。可见，盾构施工中的地层变形控制对保证建筑物安全至关重要。

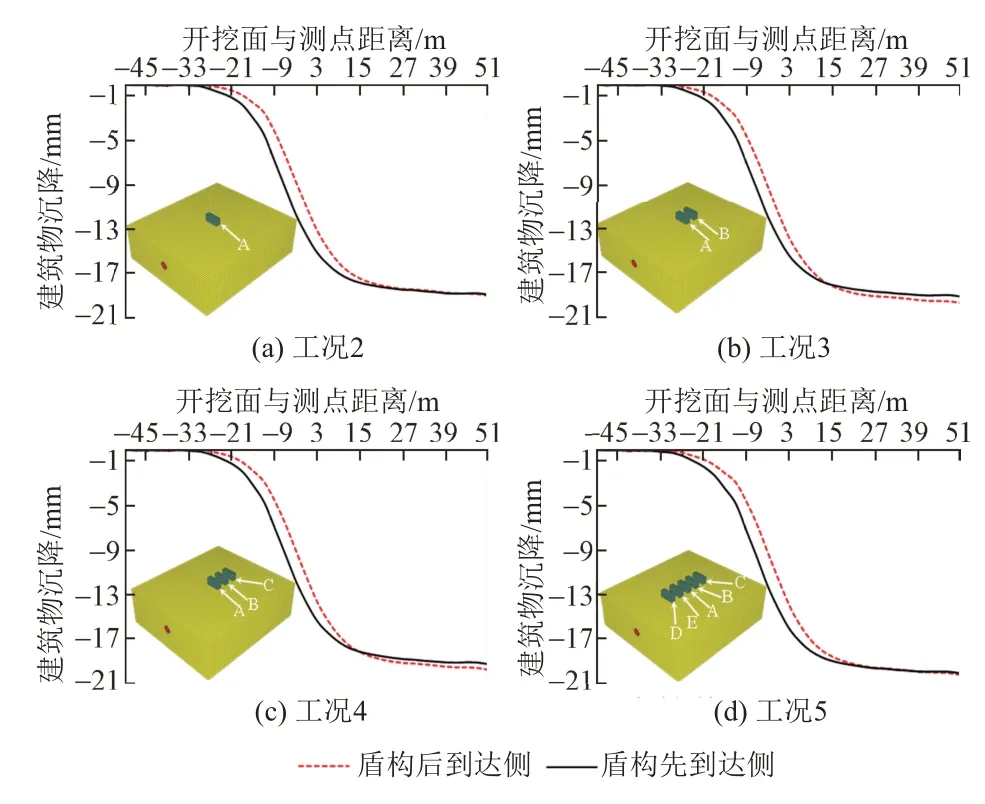
图11 掘进过程中建筑物A的不均匀沉降变化曲线

图11显示，建筑物A两侧地面超载分布形式与建筑物A在施工完成时的最终不均匀沉降关系明显。若建筑物A两侧地面超载对称分布（工况2与工况5），施工结束时建筑物A的最终不均匀沉降较小，约为0.069、0.130 mm；若建筑物A两侧地面超载不对称分布时（工况3与工况4），建筑物A在施工结束时的最终不均匀沉降则上升为0.580、0.520 mm。可见建筑物A前后两侧超载分布不对称将导致盾构施工完成时不均匀沉降急剧增大，约为对称超载时的5倍。

4.2 相邻建筑物净距对建筑物不均匀沉降的影响

改变SAB，在盾构施工模拟时对建筑物A、B前后侧的沉降变形进行监测。根据建筑物不均匀沉降数值及建筑物高度计算出盾构施工过程中的建筑物A、B最大倾角θA，max、θB，max及施工完成时的稳定倾角θA、θB。倾角随两建筑物净距的变化曲线见图12。

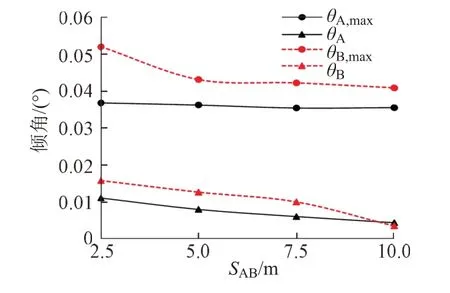
图12 建筑物倾角随建筑物净距变化曲线

由图12可知：①建筑物A、B在盾构施工过程中的最大倾角均大于施工完成时的稳定倾角，其中θA，max波动性小，稳定在0.035°左右；θB，max明显大于θA，max，约高出15%～41%，反映出前方存在地面超载将导致建筑物在盾构施工中的不均匀沉降增加的现象。SAB为2.5 m时，θB，max为0.052°，SAB=7.5～10.0 m时，θB，max稳定在0.042°左右，可见θB，max与SAB有关，最大倾角随建筑物净距的增加而减小并趋于稳定。可能的原因是盾构施工至建筑物A附近时，B处的地层变形尚未完全发展，对建筑物A的影响相对有限，建筑物A的最大倾角也相对稳定；开挖面位于建筑物B附近时，建筑物A处的地层变形已剧烈发展并对建筑物B产生较大影响，使建筑物B的最大倾角较大并随净距增大而渐减小。

②建筑物A、B的稳定倾角均随SAB增大而减小，θA由0.0110°减小为0.0040°，θB由0.0158°减小为0.0035°；除SAB=10.0 m工况外，其余工况θB比θA高出42%～65%。稳定倾角反映了盾构施工完成时建筑物的不均匀沉降，鉴于建筑物A、B沉降槽的叠加效应随净距增大而逐渐减弱，施工完成时两建筑物的稳定倾角也随净距增加而减小。