基于神经网络的飞机着陆速度预测模型*

潘卫军 张衡衡 吴天祎 刘 涛 尹子锐

（中国民航飞行学院空中交通管理学院 广汉 618307）

1 引言

美国联邦航空管理局（FAA）计划在2025年前实施下一代航空运输系统（NextGen）[1]实现国家空域系统（NAS）的现代化，在已经拥挤的终端空域中提高其容量以满足预期的交通需求增长，实现这个目标需要建立在安全间隔的前提下，为了保证航空之间的安全间隔，一个是缩减终端区的尾流间隔[2～3]，另一个是控制着陆飞机的跑道占用时间[4～5]。三是进行飞机间隔碰撞危险性分析[6]。因为上述建议都依赖于对飞机飞行进行精确的预测，基于精确的着陆速度预测和跑道占用时间预估，来提供连续到达的飞机之间的精确间隔，目前，管制程序规定了飞机在大部分空域的飞行速度，只有在飞机准备进近着陆时的进场速度由飞行员决定。着陆速度的不确定性会导致飞机间隔过大或过小，引起飞机碰撞的可能性增大或者降低终端区运行效率和机场跑道吞吐量。

当两架相继进近着陆的飞机接近着陆跑道时，前机在后机之前减速时两机之间的距离会产生压缩[7～8]。为了控制两机之间距离压缩的程度，必须在清楚前机的着陆速度后描绘出后机的进场速度变化曲线。由于管制程序没有规定确定的着陆速度，前机的着陆速度数据须通过飞机飞行数据和场面监视系统得出。本文建立了一个后机着陆速度预测模型，该模型基于前机的进近着陆速度参数进行分析计算，从而得出精确的后机进近着陆速度，使得后机以合适的速度进近着陆，在保证安全的间隔前提下，增大跑道吞吐量和机场运行效率。

2 模型数据预处理

该建模方法使用神经网络回归技术，用于构建预测模型的原始数据通常需要彻底的预处理步骤。所采用的着陆速度预测方法是多变量非线性回归，将输入值拟合成相应的历史着陆速度输出值。选择以下三步方法进行数据预处理[9～10]：数据收集、筛选和参数选择决策。

数据收集：识别和收集尽可能多的数据，保证数据集的充足性。飞行原始数据由机载的飞行参数（如燃油消耗、飞机重量等）提供。机场环境条件数据由场面监视雷达记录的数据和提供。选取成都双流机场30天的飞行数据和机场监视数据作为该模型的初始数据。

筛选：筛选出直接影响建模任务的变量上。检测对着陆速度影响最大的参数，筛选出模型输入信息中的重复和冗余信息，对整体模型精度没有影响的变量进行删除。

参数选择决策：基于筛选结果决定输入到模型的最终参数。最终模型输入值中只使用变量的实际测量值。

3 神经网络模型

3.1 基本原理

神经网络是一种基于回归的数学建模技术。神经网络可以模仿人脑的认知和推理功能，能够模拟高度非线性的行为。一般来说，当线性建模方法表现不佳时，神经网络可以作为一种替代建模方法[11]。最容易构建和实现的神经网络类型之一是前馈反向传播（FFBP）。FFBP是建立模型的良好起点，因为前馈神经网络在理论上可以拟合输入和输出之间的任何非线性关系。然而，从外部看模型是全封闭的，对于使用者就像一个黑盒子，不能看出每个输入参数是如何进行计算分析和对输出值的影响的[12～13]。

在体系结构上，FFBP神经网络由输入层、隐藏层和输出层组成，如图1所示。

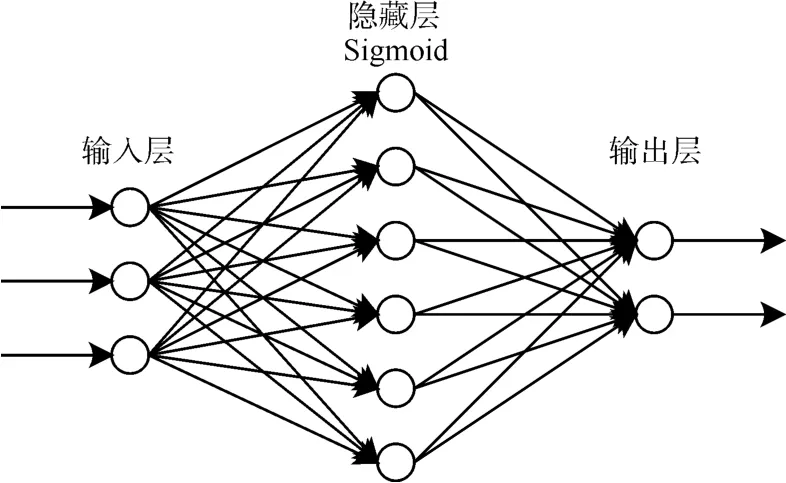
图1 三输入两输出前反馈神经网络示意图

而隐藏层是网络的数据处理中心，输出层是对模拟的响应。第一层是由神经元组成的，每个输入元素通过权重（w）连接到每个神经元，添加偏置（b）后加权输入[14]。

数学上，隐藏节点的值是通过构成逻辑函数来计算的，如式（1）所示：

使用一个符合Xi设计变量的线性函数。隐藏节点的形式如式（2）所示：

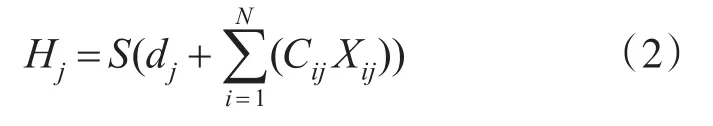
其中：dj为第j个隐藏节点的截距项；Cij为第i个设计变量的系数；Xi为第i个设计变量的值；Hj为第j个隐藏节点的值；N为输入变量的数量。

由式（1）定义的逻辑Sigmoid函数用于对输入参数进行归一化处理，使得其输出是0和1之间的值。通常，构建神经网络有三个主要步骤：训练、验证和测试。因此，数据集被分为三组。训练集（Training set）用来拟合模型，通过设置分类器的参数，训练分类模型。后续结合验证集作用时，会选出同一参数的不同取值，拟合出多个分类器。验证集（Cross Validation set）是当通过训练集训练出多个模型后，为了能找出效果最佳的模型，使用各个模型对验证集数据进行预测，并记录模型准确率。选出效果最佳的模型所对应的参数，即用来调整模型参数。最后测试集（Test set）通过训练集和验证集得出最优模型后，使用测试集进行模型预测。用来衡量该最优模型的性能和分类能力。即可以把测试集当做从来不存在的数据集，当已经确定模型参数后，使用测试集进行模型性能评价[15]。

在现有的许多神经网络训练算法中，当需要快速训练时，Levenberg-Marquardt的算法是前馈网络最常用的算法。基于该研究的目标，为了对输入变量进行回归建模以预测相应的着陆速度，使用网络训练方法进行函数逼近。神经网络训练需要基于已知输入和对应目标输出的训练集。神经网络也可进行多次训练以提高拟合质量。使用式（3）中定义的均方误差（MSE）性能函数作为训练过程停止的标准[16]。

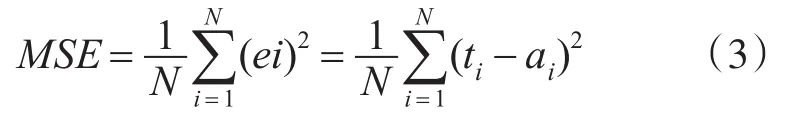
其中：MSE为均方误差即神经网络输出结果和参考结果之间的均方误差；ei为第i个神经网络输出结果和参考结果之间误差；ti为第i个参考结果；ai为第i个神经网络输出结果。

3.2 模型评估

模型评估中包括神经网络模型的预测着陆速度误差和参考速度误差，为了进行比较，定义了以下两个指标。

参考误差：实际着陆速度和参考速度之间的绝对差值。

模型误差：定义为实际着陆速度与神经网络模型预测的着陆速度之间的绝对差值。

其中：VActual为实际速度为地面速度和机场报告风速之和；VTarget为参考速度为基于飞机类型和飞机重量的飞行手册推荐的进近速度，此速度用作比较的参考着陆速度；VModel为神经网络模型预测的着陆速度。

每种飞机都有飞行操作手册，其中有基于飞机类型和着陆飞机重量的着陆速度称为参考速度。为了评估着陆速度模型的质量，将其预测结果与参考结果进行比较。模型数据使用的飞机类型是A320，最常见的单通道飞机之一。对于这种飞机类型，飞行操作手册定义：弱阵风条件降落和强阵风条件降落，定义为阵风低于10kn为弱阵风条件，阵风大于10kn为强阵风条件[17]。

在弱阵风条件下，操作手册建议飞行员将进近参考速度定为

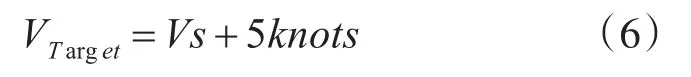
其中：VTarget为参考最后进近速度；Vs为标准最后进近速度，其作为该型飞机静风时的最后进近速度。

在强阵风条件下，操作手册建议飞行员的参考速度为

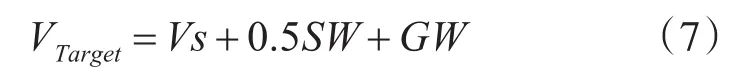
其中：VTarget为参考最后进近速度；Vs为标准最后进近速度，其作为该型飞机静风时的最后进近速度；SW为定常风，即为所报告风的逆风分量；GW为阵风，即报告风和报告阵风之间的逆风差异。限制条件是 0.5SW+GW不得超过20kn[18]。

确定选定机场固定参数（如机场高度、跑道长度）有助于飞机的最终进场性能。此外，每种飞机类型（如B737或A320）都有直接影响其着陆速度的特定性能参数。为了解决所有这些可能影响着陆速度模型的准确度的参数，使用历史数据创建选定机场和选定飞机的着陆模型。

本模型所提出的神经网络模型使用成都双流机场（CTU）的A320飞机类型的30天共计5569架次进近着陆数据。

第一步：数据收集

本研究使用的原始数据集包含300多个变量。这些数据包括机场跑道信息（例如跑道长度和配置）、气象环境信息（例如能见度、风力条件）、特定飞行参数（例如飞行的城市、燃料燃烧率、着陆重量等）以及A320飞机进近着陆的参数（如重量、飞机最大有效载荷）。

第二步：筛选

筛选即对参数预测值的识别。筛选分两步进行：消除无关性数据和消除模型的重复信息[19]。一开始就被确定为不相关的变量会被自动消除，冗余的消除是基于变量对之间的统计相关性，如果两个或多个变量提供相同的信息，则计算分析时只使用其中一个。

第三步：选择决定

基于尽可能使用最少数量参数的原则，最后筛选出的结果中包含与飞机着陆速度最相关的十三个参数的简化集合。然后，为了将该建模方法适用于其他机场，从中排除了其他机场不可获取的变量。最后，数据处理的结果是表1所示的五个变量参数。用表1选定的五个变量用作建立神经网络模型的输入变量，输出则是着陆速度。

表1 模型所需的变量

4 神经网络建模及运算

因为参考着陆速度预测是根据着陆阵风条件来划分的，所以数据也分为两组：弱阵风和强阵风条件。

表1所示的五个输入变量用作模型输入，使用Matlab软件为两种阵风条件建立前馈神经网络。图2所示的神经网络示意图有三个隐藏层和一个输出层。

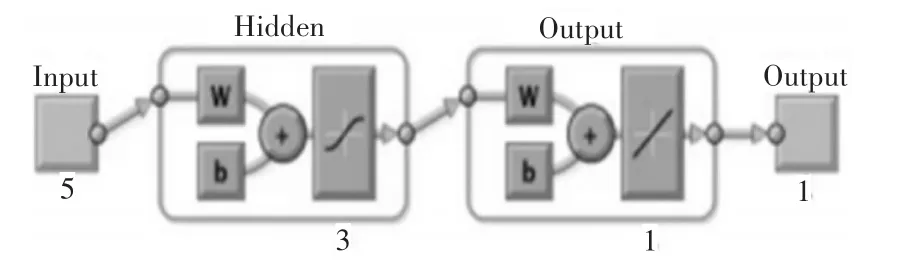
图2 神经网络简介图

基于在可用数据点数量有限的情况下允许足够大的训练集大小，数据集被随机分成如下三组：70%用于训练，20%用于验证，其余10%用于测试。训练过程包括调整权重和偏差，直到验证数据集收敛。

在图3所示的强阵风情况的例子中，收敛发生在第六次迭代之后。

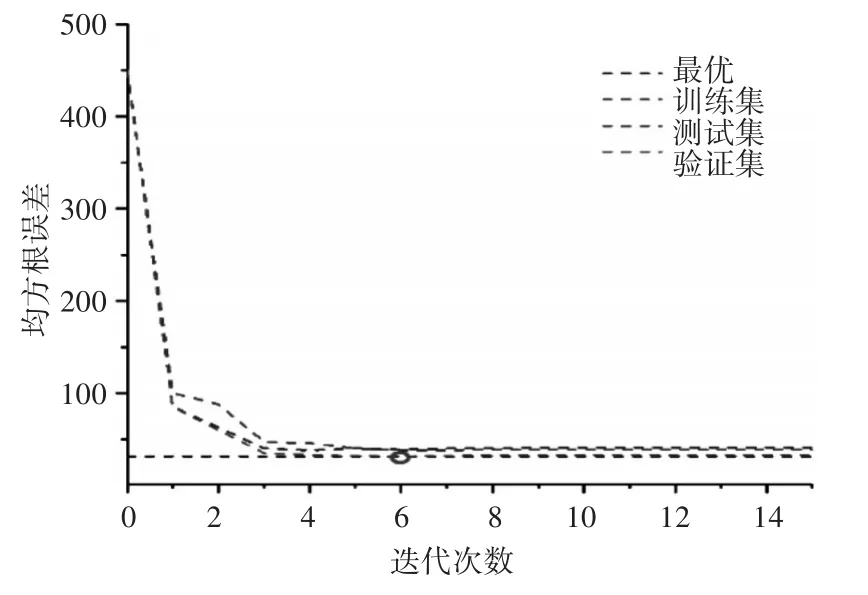
图3 强阵风条件下的均方误差

5 结果分析

在建立模型和预测着陆速度之后，进行评估预测的质量。图4和图5分别表示了弱阵风和强阵风时实际着陆速度与预测着陆速度的函数关系，如果模型能精确预测实际着陆速度，所有的红三角都会落在绿线上。

预测结果的质量使用确定R2系数和均方根误差进行评估。对于上述数据集，弱阵风的R2误差和均方根误差分别为0.42和3.48，强阵风条件下分别为0.57和3.5。

此外，从图4和图5可以推断，尽管使用相同的数据集进行建模和测试，但在弱阵风和强阵风条件下，着陆速度预测存在相当大的偏差。

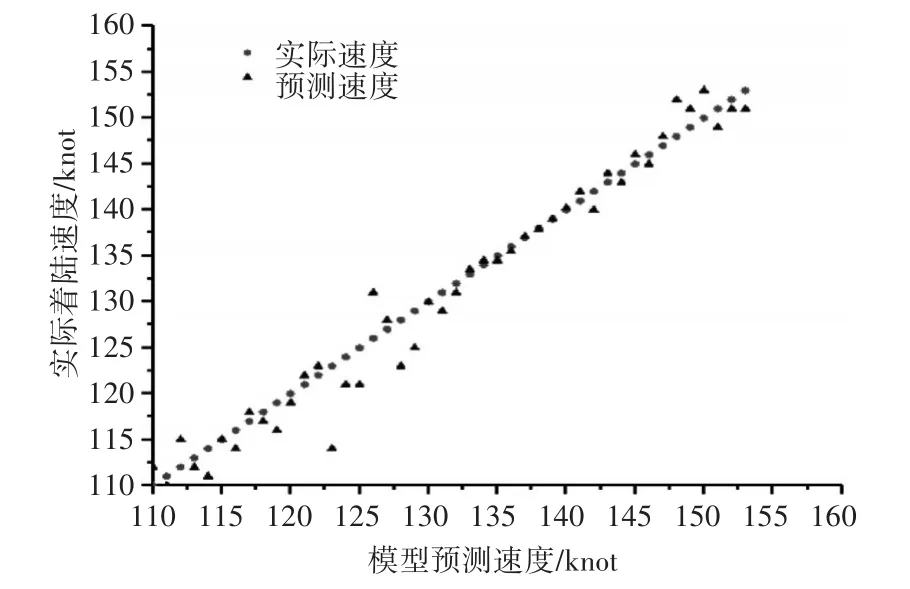
图4 弱阵风条件下实际速度与预测速度对比图

基于图4和图5所示数据点的聚集性质，表明实际和预测着陆速度呈现正态分布特征。因此，模型误差分布也具有正态分布特征。

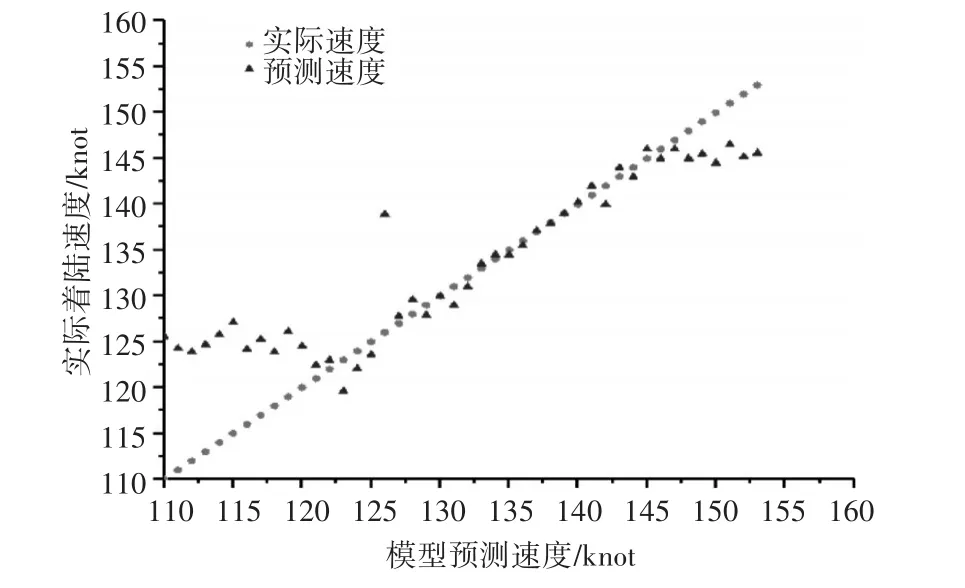
图5 强阵风条件下实际速度与预测速度对比图

如图6所示的正态概率图所示，因为所有数据点都落在测线附近，正态分布的假设对于弱阵风条件是合理的，对于强阵风情况，也观察到类似的趋势。因此，正态分布统计可以用来比较模型结果与其相应的标准之间的差异。表2是计算出的统计参数的汇总。

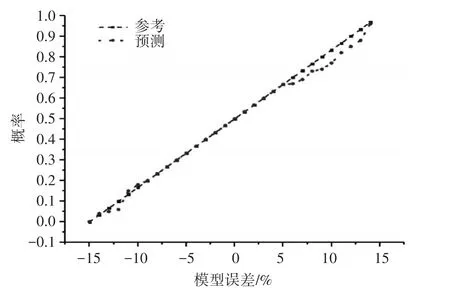
图6 弱阵风条件下正态概率图

表2表明，弱阵风和强阵风条件下模型结果误差平均值比参考值小一个数量级。此外，模型结果的偏差值小于参考结果的偏差值。表2统计数据表明，神经网络着陆速度预测模型结果在弱阵风和强阵风条件下都优于参考结果。

表2 着陆速度误差统计总结

对于两种阵风条件，模型结果和参考结果的误差分布近似为正态分布，如图7和图8所示，神经网络模型的方差较低。对于弱阵风条件，模型结果误差从25%～75%的扩展为5.3%（-3%～2.3%），而参考结果误差的扩展为6.6%（0.8%～7.4%）。

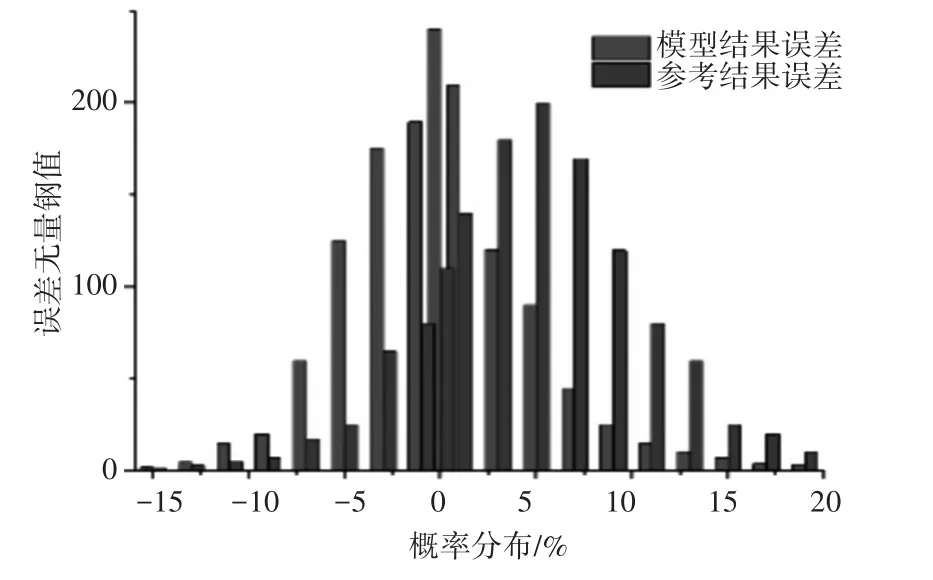
图7 弱逆风误差分布

类似地，对于强阵风条件，从模型结果误差的25%～75%的扩展是5.3%（-3%～2.3%），参考结果误差扩展是5.7%（-9.9%～-4.2%）。

在弱阵风情况下，当模型结果误差的峰值为0时，参考结果误差的概率密度函数达到约5%的最大值，即参考结果误差显示系统误差分布向右移动。相比之下，对于强阵风情况，参考结果误差分布向左移动，概率密度函数最大值约为8%。

对弱阵风条件的定量分析表明，神经网络建模方法结果提供了比参考结果更准确的着陆速度预测。第一因为神经网络模型误差分布的平均值约为0%，这表明它们比参考结果具有更高的精度。第二因为神经网络模型结果误差在弱阵风和强阵风条件下的标准偏差分别为4.2和4.0，而参考结果误差的标准偏差在两种情况下为4.9和4.4。

实际上神经网络模型结果误差分布说明弱阵风和强阵风的误差分布标准偏差分别减少了18%和9.5%。即对于弱阵风和强阵风，神经网络模型结果误差相比参考着陆速度结果误差分别减少了18%和9.5%。

根据图7，对于弱阵风条件，飞行操作手册给出的参考结果倾向于低估着陆速度；即在弱阵风条件下，与飞行手册推荐值相比，飞行员的着陆速度超过了参考着陆速度。相比之下，在图8所示的强阵风条件误差分布中，飞行操作手册给出的参考速度超过了实际着陆速度。

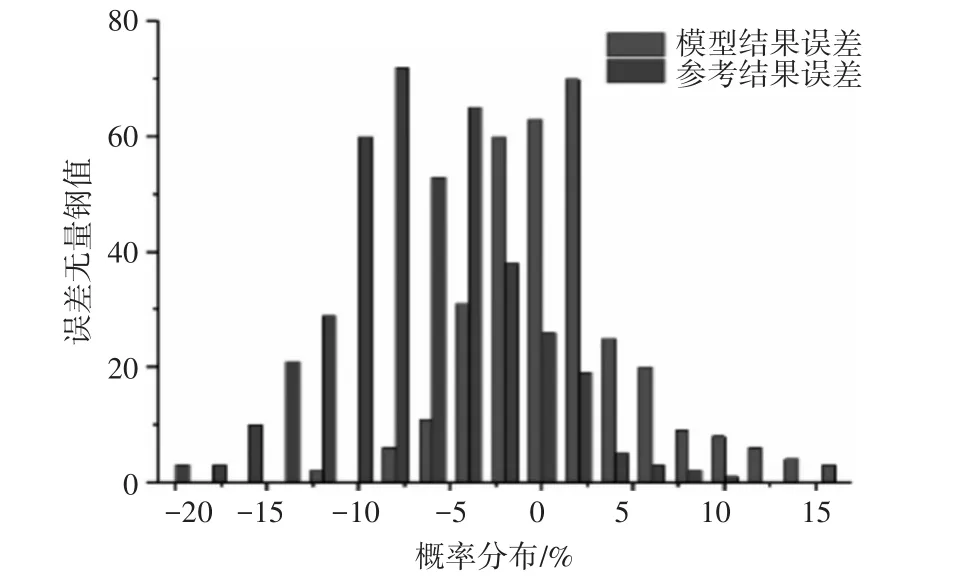
图8 强逆风误差分布

总之对于正常的着陆速度范围，神经网络建模方法能够精确的预测大多数数据点的着陆速度。

6 结语

为表1中所列变量开发的神经网络的拟合质量通过确定系数R2进行评估，弱阵风模型的确定系数为0.43，强阵风模型的确定系数为0.56。基于误差分布的正态分布性质，发现神经网络模型在96%的情况下准确预测着陆速度，在弱阵风条件下误差为12.2%，在强阵风条件下误差为11.9%。在使用窄体飞机作为实验机型的情况下，神经网络模型将弱阵风和强阵风条件下着陆速度预测的不确定性分别降低了17.2%和9.35%。此外，飞行员在弱阵风条件下倾向于过补偿着陆速度，在强阵风条件下倾向于欠补偿着陆速度。