海上搜救力量配置问题研究*

任东彦

（海军军医大学海军卫勤训练基地 上海 200433）

1 引言

海上搜救是一个世界性难题，特别是海上作战中对落水人员的搜救工作难度更大。这是由于海上环境恶劣，且海域广阔，伤员分布广泛，人员落水后，若长时间得不到救治，受低温、海洋有害生物侵袭、淡水和食物缺乏等影响，极易死亡，因此，加强战时海上落水人员搜救工作的相关研究具有十分重要的意义。海上落水人员包括由于战损、碰撞、故障、触礁、火灾、倾覆、进水、失控等各种原因而导致的处于海面险境的舰船落水人员、战斗机落水飞行员等人员，对落水人员搜救的关键是争取时间[1～2]。这其中，搜救力量能否科学配置并迅速准确到达搜救海域是搜救工作成败的关键，本文针对海上搜救力量配置问题进行研究，在定性分析的基础上建立海上搜救力量配置解析模型，为海上搜救力量配置提供理论参考，有助于提高海上搜救效率。

2 搜救作业区的优化配置

达到高效率，是海上搜救工作所要达到的基本目标之一。为了以最快速度搜索到落水人员，海上搜救力量配置的前提是要合理划分搜救作业区。

2.1 搜救作业区的选择

在搜救过程中，为了将搜救区域限制在尽可能小的范围内，需要确定基本搜救区。基本搜救区就是根据已知落水人员信息或已发现落水人员的位置结合海区海流流向和风向初步确定的搜救区。理论上，基本搜救区的形状可以有很多种，但在实际应用中，为便于搜救行动，一般情况下，多将搜救区确定为矩形。确定基本搜救区的原则是搜救区既包含所有搜救目标又满足面积最小。

按照这一原则，基本搜救区是包含某一组中所有搜救目标且面积最小的外接矩形。为满足这一要求，就要针对已发现搜救目标计算多个面积。一般而言，由于这里所确定的搜救区仅仅是概略的，因此只要大致方向差不多就可以满足要求，例如选取0，60°，90°三个方向的外接矩形进行计算和比较，从中选出面积最小的。但现代搜救舰船多携带有直升机，对直升机搜救而言，风向对直升机飞行稳定性、航迹保持和悬停点间的过渡影响很大。因此，在对基本搜救区进行选择时，一般按照风向选择外接矩形[3]。

2.2 搜救作业区的合理划分

当搜救海域面积较大时，为便于搜救行动，可将搜救作业区划分为若干地段，对每个地段编号并划定作业区，由搜救力量按编号逐段搜索。划分搜救地段时按下列要求进行。

1）尽量将某一类搜救目标划分到一个作业区内；

2）保持搜救带为直向配置；

3）便于转向机动。

2.3 搜救方向的确定

搜救方向是指舰船或直升机在划分好的搜救作业区内实施搜索时的起始方向。确定搜救方向时，应根据下列情况综合分析比较，抓住主要矛盾：

1）尽量与搜救作业区边长方向一致；

2）尽量与风向平行，以便直升机搜索发现目标时迎风悬停；

3）便于舰船和直升机转向机动；

4）尽量减少转向次数。

2.4 搜救起点和顺序的确定

搜救起点是指舰船或直升机在划分好的搜救作业区内实施搜索时的起始位置。确定搜救起点，应考虑下列因素：

1）一般应从搜救作业区边缘开始，逐带顺序搜索，也可从航道或地域中心线开始，逐带向两侧扩大；

2）搜救带按顺序以罗马字母标注，确定了搜救起点，也即确定了搜救的顺序。

3 海上搜救方法

海上搜救一般结合具体任务由舰船或直升机完成。实施海上搜救，搜索目标是前提，只有及时准确地搜索到目标才能实现以最大的效率救治目标。在搜救过程中，多数情况下，应根据搜救任务的需要，在搜救作业区的优化配置的基础上，进一步确定搜救方法。搜救方法就是指舰船或直升机相邻搜索带之间的配置方法[4～5]。搜救方法为相邻搜索航路的搜索宽度之间有一定的重叠，重叠宽度一般为二倍航迹均方误差（2δ），见图1。搜索带的实际宽度，可按下式求得：BS=B-2δ。

图1 搜索航线

4 海上搜索样式

搜索样式是指在确定搜救作业区的位置、大小、形状后，对搭载搜索设备的搜救力量在搜救作业区的路线规划和运用方式。选择搜索样式的主要依据有落水人员位置坐标预测的准确性、搜救作业区的大小和形状、搜救力量的定位精度。适用于对海搜索的方法主要有扇形搜索、扩展方形搜索、横移线搜索和平行线搜索。分析四种搜索方式，对比如表1所示。

表1 搜索方式对比

从表1中可以看出，扇形搜索样式和方形扩展搜索适用于定基点小范围的小散布区域落水人员的搜索，但不适合多个搜救力量协同搜索；平行线搜索适合于不定基点的大范围区域搜索，能够运用多种搜救力量协同搜索；横移线搜索适合不定基点的长且窄的大范围区域搜索，适合直升机或舰机协同搜索。

5 海上搜救力量配置算法

战时，为了提高海上落水人员救治效率，要求搜救兵力在规定的时间内必须完成规定海域的搜索，因此，提高海上落水人员救治效率的前提是要达到较高的搜索效率。在搜救作业区满足战术要求并合理划分的基础上，应科学配置搜救兵力并迅速完成各项搜索任务。

假设在某海域内（面积为S）内实施搜索，预先只了解该海域存在落水人员，并不了解有关落水人员的具体位置。可假设目标在该区域内均匀分布，在搜索过程中，将搜索海域划分为若干小段（设其个数为n），每一小段采用平行线样式对搜索海区进行覆盖。

搜索区域是长为L1、宽为L2的矩形，搜索宽度为l，搜救力量速度为v，相邻搜索带之间的重复区域为二倍航迹均方误差（2δ），每次180°转向所需的时间为Δt。

搜索区域面积即为L1·L2，如图2所示。则目标出现在某一小段之内的概率为

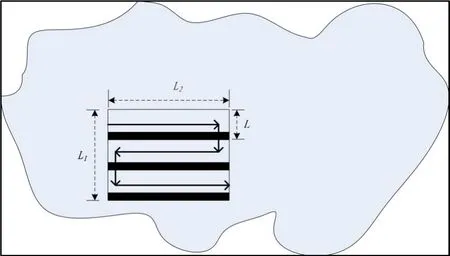
图2 平行线搜索覆盖区域

如图2根据几何关系可得，对该矩形搜索区域进行一次全覆盖搜索，搜救力量所需要往返次数为

其中n1为进位取整的正整数。

则搜索力量搜索过的航路距离长为

所需的时间为

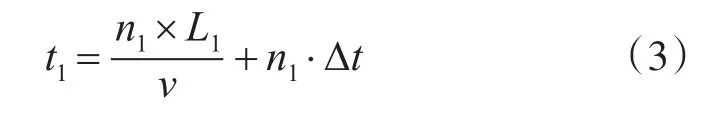
由此，在计算海上搜救力量配置数量时，可结合具体的搜救任务，根据要求的搜救时间t1反向计算出航线距离长为d1和搜索力量所需要往返次数为n1，进而可计算出海上搜救力量配置数量。

6 示例

假设在某次海上作战中，红方1艘护卫舰被敌方一枚反舰导弹击中，导致15名人员落水（位远海某岛西南15海里附近海域），见图3。编队指挥部接到求救信号后即组织搜救舰船对落水人员的搜救。

1）搜救作业区的优化选择

根据受损舰船位置或已知落水人员信息或已发现落水人员的位置并考虑风向、海流流向等海区地理水文气象资料，初步将70°方向的外接矩形确定为搜救作业区，编号为S，搜救作业区长L为10km，宽W为6km，如图3所示。

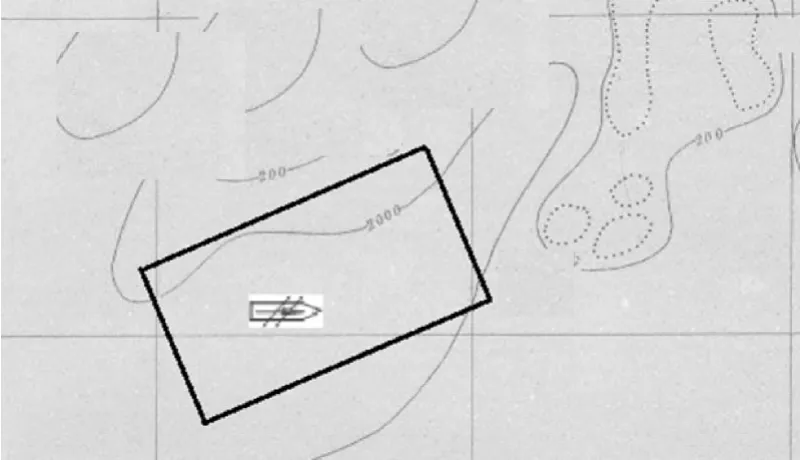
图3 受损舰船搜救作业区

2）海上搜救力量配置数量

在S海域内实施搜救，因为预先只了解该海域存在落水人员，并不了解有关落水人员的所有具体位置，可假设目标在该区域内均匀分布。根据对海上落水人员的搜索样式分析，平行线样式完成全覆盖的时间更少，所需航路距离更短，具有较高的搜索效率。可将搜索海域划分为若干小段（设其个数为 n），编号分别为 S1，S2，…，Sn，每一小段采用平行线样式对搜索海区进行覆盖，n即为搜救力量配置数量。

考虑伤员的时效救治，上级要求搜救兵力在1h内必须完成全部海域的搜索；搜索海域S1，S2，…，Sn是长L1为10KM，宽为L2待定的矩形区域，搜索宽度l综合考虑海区气象条件设定为1000m，搜救舰船速度v设定为15kn，相邻搜索带之间的重复区域（二倍航迹均方误差2δ）设定为50m，舰船每次180°转向所需的时间Δt设定为3min。

根据几何关系可得，对该矩形搜索区域进行一次全覆盖搜索，搜救力量所需要往返次数为

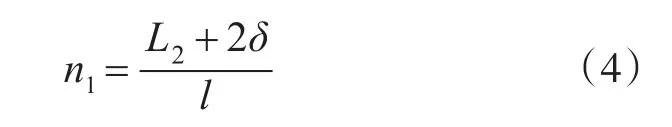
其中n1为进位取整的正整数。

所需的搜救时间为

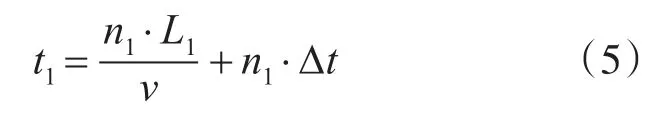
且满足约束条件：t1≤1。

由式（4）、（5）可计算出搜救海域宽L2，则：搜救力量配置数量为

其中n为进位取整的正整数。

将数据代入式（4）、（5）、（6）计算可得：

由于n为进位取整的正整数，则：n=3。

根据计算结果，完成上级要求在1h内对全部海域的搜索，指挥部结合现有搜救力量，需至少配置3艘搜救舰船分别完成对搜索海域S1，S2，S3的搜索，见图4。

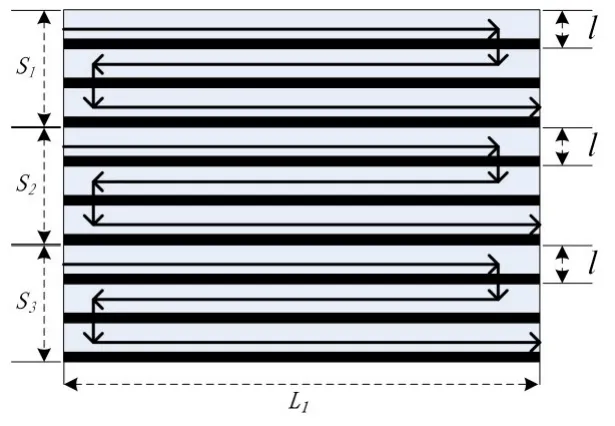
图4 平行线搜索覆盖区域

7 结语

由于海上环境的复杂性，各国海军都十分重视海上搜救的研究。本文首先对搜救作业区的优化选择方法进行了研究，明确了舰船或直升机在划分好的搜救作业区内实施搜索时的起始方向、搜救起点和顺序，在对海上搜索方法和搜索样式分析的基础上，重点对海上搜救力量配置数量计算方法进行研究，在定性分析的基础上建立海上搜救力量配置解析模型，以期进一步丰富海上搜救理论，为海上搜救力量配置提供理论依据，辅助海上搜救指挥决策。