基于PCA算法和K-means聚类算法的医用耗材库存分类管理研究

张林灵，郑焜

1. 浙江大学医学院附属儿童医院 a. 医疗设备科；b. 后勤保障部，浙江 杭州 310052；2. 国家儿童健康与疾病临床医学研究中心，浙江 杭州 310000

引言

医用耗材是指经药品监督管理部门批准的使用次数有限（包括一次性及可重复使用）的消耗性医疗器械[1]。自2019年国家发展改革委提出“取消公立医疗机构医用耗材加成”[2]以来，公立医院资金周转压力变大，医用耗材管理跃变为公立医院的管理重点[3]，其中医用耗材库存管理尤为重要[4]。这就需要医院的医用耗材管理部门对医用耗材进行有效的库存管理，采用科学严谨的管理方法，在不影响医院运营的情况下，提高医院的经营效益。

为了降低医院库存成本，Rosales等[5]研究了定期补货策略与连续补货相结合的混合补货策略。Akcan等[6]提出了库存可以与供应商共同管理的模式。Zhang等[7]研究了两个独立医院之间的库存共享机制的运作。目前，国内普遍医院将医用耗材分为低值医用耗材与高值医用耗材两类来管理[8-11]，低值医用耗材通常采用基本库存量备货的库存管理办法，高值医用耗材通常采用“零库存”模式来管理[12-14]。虽然对医用耗材做了分类，但是分类标准不明确且易受到客观因素的影响[15]：① 在库房管理系统中，并未对低值医用耗材和高值医用耗材做出明确的区分，完全依靠库房管理人员和临床科室的主观判断；② 临床科室使用的高值耗材种类繁多、更新频繁，难以确定高值医用耗材清单。模糊的医用耗材分类会引起混乱的库存管理，这不仅会影响日常医疗服务的开展，还会增加医院的资金压力。考虑到医用耗材的特征维度具有多样性，如价格、有效期、到货周期、消耗量、科室数量等，不利于提取关键特征维度。且为了便于制定简明清晰的库存管理策略，分类类别不宜过多。本文提出一种基于主成分分析（Principal Component Analysis，PCA）算法和K-means聚类算法的医用耗材分类方法，并制定相对应的库存管理策略，预期在降低医用耗材库存成本的前提下提高库存的有效性。

1 方法

本文以某儿童医院2020年全年医用耗材历史数据为基础，随机抽样100种医用耗材数据进行研究。

1.1 PCA算法

考虑到信息中包含过多的维度会使得研究变得复杂，并且某些维度之间存在相关性，本文选用PCA算法对医用耗材的多维度信息进行降维处理。PCA算法是一种在降维中使用非常广泛的无监督算法，主要目的是用较少的维度去表达原始数据[16]。本文使用100个样本数据，每个样本有9个维度，分别是价格、月消耗量、到货周期、有效期、周转天数、存贮温度、外包装体积、使用科室数量、不良率，构成一个100×9阶矩阵，见式(1)。

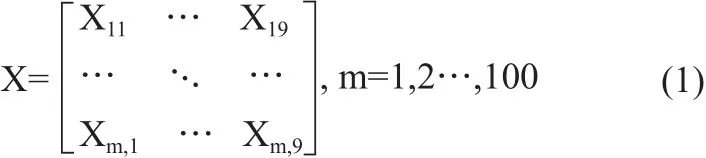
PCA算法将9个特征向量综合成K个新的特征向量，即主成分。在进行主成分分析前，需要先对数据进行预处理。由于各个维度的量纲不同，需要先对各个维度进行零均值化处理，再采用标准差标准化法，见式(2)。

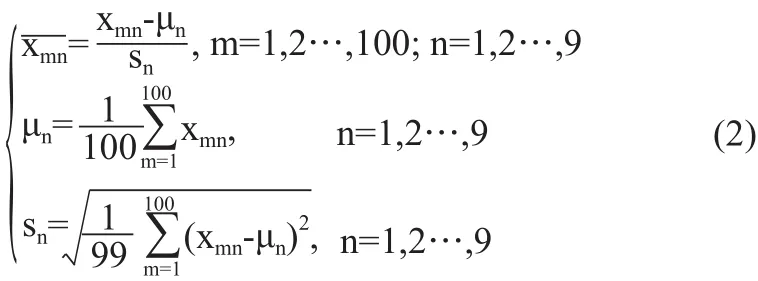
主成分分析步骤如下：

（2）对协方差矩阵进行对角化处理，求得协方差矩阵C的9个标准正交特征向量，并按照对应的特征大小进行排序，特征值与特征向量一一对应。

（3）根据各个成分累积贡献率的大小选取前K个主成分，见式(5)。

1.2 K-means聚类算法

K-means是聚类算法中最经典、最实用的无监督算法，能够将一个没有标签的数据集进行大致的划分，最终使得每个数据点都有固定的类别[17]。本文以100个样本数据为数据集X，K-means算法的工作流程如下：

（1）根据对数据集X的先验知识，确定数据集X的类簇数k。

（2）在X中随机指定k个数据点作为首次聚类的k个类簇的中心点ci(i=1,2,…,k)，其中，每个中心点同样具有d维属性，即cij(j=1,2,…,d)。

（3）计算除中心点之外的其余数据点与k个中心点的距离，根据计算结果，将其余数据点分配到最邻近的那个中心点所属的类别，最终形成k个类簇ci。距离计算一般使用欧氏距离计算公式，见式(6)。

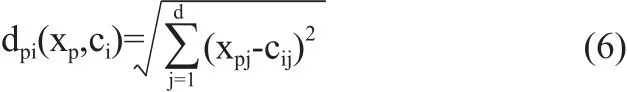
（4）由于第（2）步中的中心点为随机指定，所以需要重新计算各个新得到的类簇ci中所有数据点的d维度均值，将计算结果赋值给新的中心点。如此往复步骤（3）～（4），直至聚类目标函数收敛。本文采用簇内误差平方和作为目标函数，其定义如式(7)所示，式中的x代表属于簇ci的所有数据点。

1.3 确定最佳类簇数

由于K-means聚类算法是无监督算法，所以无法用交叉验证的方法来评价算法结果[17]。轮廓系数是评价聚类效果的最常用方式[18]，本文选用轮廓系数来确定最佳类簇数，计算方法如下：

（1）计算样本xi到同簇其他样本的平均距离a(i)。定义a(i)为样本xi的簇内不相似度。a(i)越小，说明样本xi越应该被聚类到该簇。

（2）计算样本xi到其他簇类Yj的所有样本的平均距离bij，称为样本xi和簇Yj的不相似度。定义bij为样本xi的簇间不相似度，b(i)=min{bi1,bi2,…,bik}。

（3）根据样本xi的簇内不相似度a(i)和簇间不相似度b(i)，样本的轮廓系数s(i)计算公式如式(8)所示。

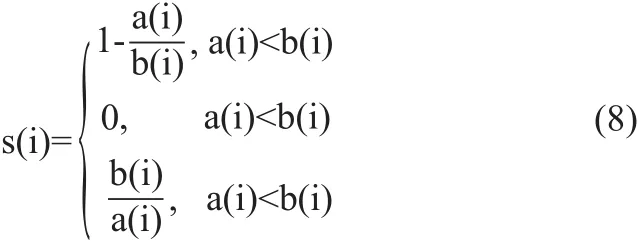
所有样本的s(i)的均值称为聚类结果的轮廓系数。

2 结果

利用PCA算法对随机抽样的100种医用耗材数据提取其主成分。有研究表明累积贡献率e≥95%能够较好地解释原始数据[19]，所以提取4个主成分，结果如表1所示。

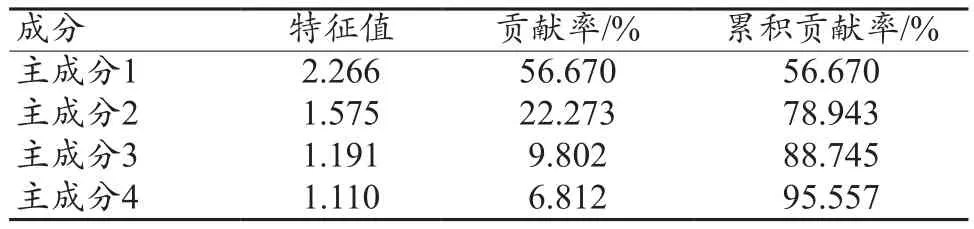
表1 主成分贡献率和累积贡献率

根据主成分特征值对应的特征向量得到主成分向量分别为F1、F2、F3、F4，从而得到最终降维结果F的表达式，见式 (9)。

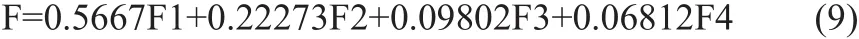
其中，F1、F2、F3、F4特征向量的系数如表2所示。

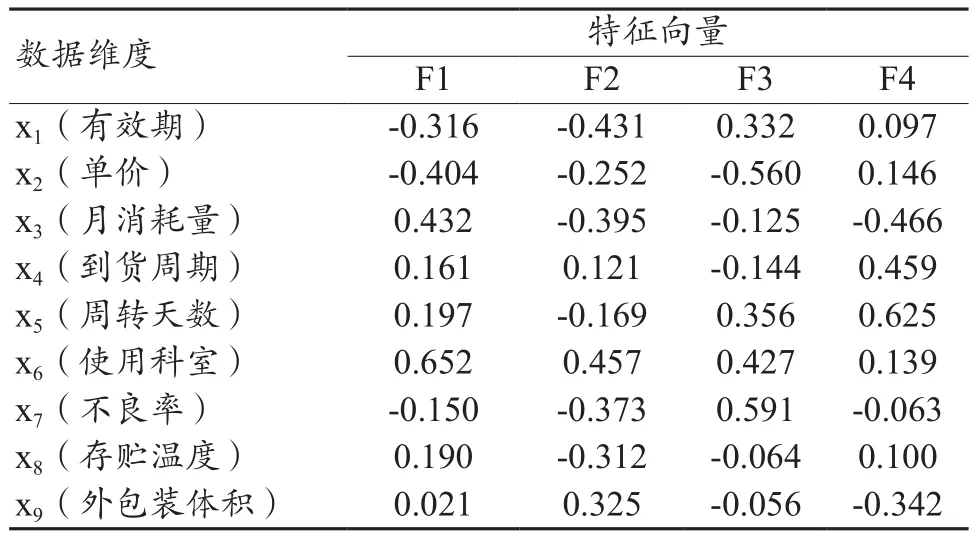
表2 各主成分特征向量的系数

将PCA后的降维结果F作为K-means的计算数据集，对数据集进行分类。由于K-means算法需要指定类簇数k，同时考虑到医用耗材分类过多或过少都不利于管理的实际情况，本文选取k值为2～10计算轮廓系数，从而确定最佳类簇数。经计算各k值下的轮廓系数如图1所示。

轮廓系数越大，表示簇内各数据点之间越紧凑，簇间距离越大，聚类效果越好[20]。由图1可知k取3、4、5、6时的聚类效果相对较好，同时考虑到库存管理的实际可操作性，故选取k值为3较为合理。K-means算法将100种医用耗材分为三类的结果如下。

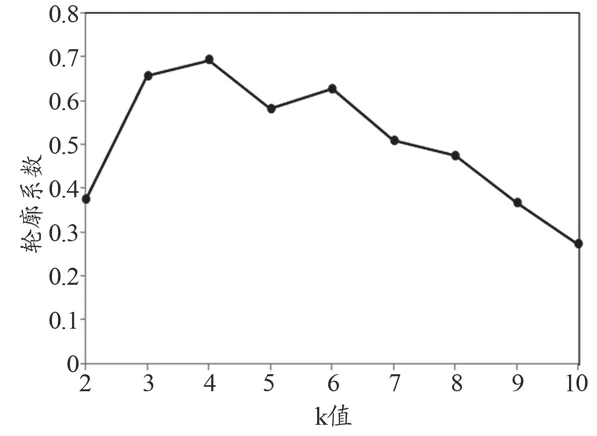
图1 各k值下的K-means聚类结果的轮廓系数

（1）第一类医用耗材共有44种，列举其中20种如表3所示。第一类医用耗材普遍具有单价低、使用科室多、使用量大的特点。而且第一类医用耗材对保证医院的运转非常重要，需要保证其不出现短缺的情况。在库存策略上适当增加该类医用耗材库存，例如按临床需求量上浮10%储备。这样既能保证临床可能出现的计划外需求，又不会给医院现金流造成压力。

表3 第一类医用卫生耗材

（2）第二类医用耗材共有42种，列举其中20种如表4所示。第二类医用耗材普遍具有单价比较高、使用科室少、消耗量大的特点，且对维持医院正常运转起到非常重要的作用。这类医用耗材需要在日常管理中给予最大关注。在库存管理策略上，一方面需要时刻关注它们的消耗量；另一方面，为了降低库存持有成本，它们的安全库存应维持在较低水平，例如按日常临床需求量上浮5%储备，以保证不断供。

表4 第二类医用卫生耗材

（3）第三类医用耗材共有14种，结果如表5所示。第三类医用耗材普遍为非必要的医用耗材，为三类医用耗材类别中重要性最差的一类。在采购策略上实行周期性采购，同时控制采购的数量以降低不必要的经费支出。在库存策略上采用零库存管理，按照采购周期，到货后一次性全部领用出库给临床使用科室。

表5 第三类医用卫生耗材

3 应用实践

将本文研究的基于PCA算法和K-means聚类算法的医用耗材库存分类管理方法模拟运用到某儿童医院2021年第一季度的医用耗材库存管理中，模拟对象依旧选取上文研究中抽样的100种医用耗材。以库存金额、周转天数以及响应时间为指标，将模拟结果和2021年第一季度的实际数据进行对比，对比数据如表6所示。

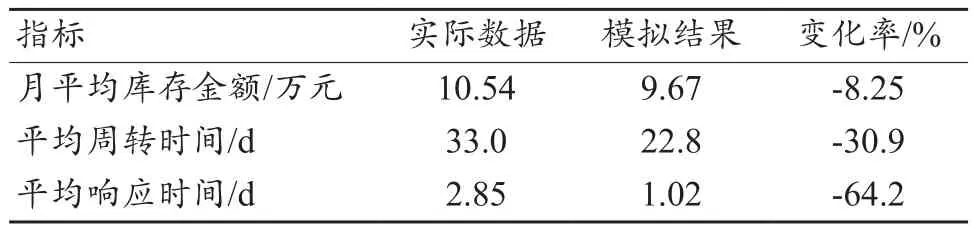
表6 2021年第一季度医用耗材库存管理模拟结果和实际数据对比

从表6中可以看出，月平均库存金额的模拟结果较实际数据减少了8.25%，医用耗材库存周转天数模拟管理后提升了30.9%，有效降低了库存对医院资金流的不利影响。除此之外，模拟管理使得医用耗材库房对临床科室的医用耗材需求响应天数降低了64.2%，大大提升了库存的有效性，同时也提升了医院临床科室的服务质量。

4 讨论与总结

针对医用耗材分类标准不明确、库存管理易受主观因素影响的问题，本研究提出利用PCA算法和K-means聚类算法对医用耗材进行分类，将医用耗材分为三类，对三类医用耗材采用不同的库存策略。并对2021年第一季度的历史数据进行模拟实验，实验结果表明本文研究的分类方法能够降低库存成本，同时提高库存的有效性。

将本文研究的方法与其他关于库存分类的方法进行对比，相较于谢海源等[21]提出的专家系统分类法，由于专家系统的设计需要知识库、推理机、综合数据库等结构，是一个复杂的程序系统，本文使用的方法只根据数据特性进行分类，具有依赖性少、简单高效的优势。对比陈震等[22]提出的ABC-VED矩阵分类法，本文研究的方法从模拟的结果来看，资金占用率、周转天数、平均响应天数的提升效果都优于ABC_VED矩阵分析法，同时ABC_VED矩阵分析法需要人工将每种耗材进行标记归类，依赖于分类人员的主观性，而本文使用的方法提取耗材的数据特性进行分类，具有客观性强、效率高的优势。

当然，本文使用的研究方法也存在一定的局限性，比如PCA算法在非高斯分布情况下，得出的主元可能并不是最优的；K-means算法中聚类簇数需要人为指定，并多次取值进行分类效果的比较，方可确定最佳聚类簇数。但对于医用耗材分类而言，PCA算法和K-means聚类算法有不错的效果。