基于鲁棒接续时间的铁路空车调运优化

罗 霞 ，胡剑鹏 ，甘易玄

（1.西南交通大学交通运输与物流学院, 四川 成都 611756；2.西南交通大学综合交通运输智能化国家地方联合工程实验室, 四川 成都 611756）

空车调运是实现铁路资源优化配置的重要内容，空车调运的优劣直接影响铁路车辆的利用效率、市场需求的满足程度以及运输组织的现代化水平.

近年来空车调运优化问题的研究多从供需及环境的随机性出发建立动态随机规划模型.文献[1]基于广义旅速建立时空服务网络，提出了空车调配多阶段动态优化方法；在此基础上，文献[2]着重考虑了实际运输生产中的能力约束，建立了考虑车种替代动态规划模型；文献[3]则将空车调配分为基于固定需求的优化调整和基于客户实时需求的策略再优化两个阶段，解决了空车需求的动态变化问题；文献[4]基于供需的不确定性，为约束条件和目标函数设置了一定的置信水平，建立了多车种调配优化模型；文献[5]考虑了路网中转能力和通行能力不确定性的影响，建立多目标随机期望约束模型；文献[6]则针对列车走行时间的不确定性，提出了鲁棒优化模型，并利用对称和对偶变化降低了模型求解难度，提高了求解效率.

在上述研究的基础上，考虑到实际铁路生产中空车的产生以及空车的需求是一个时空问题，除了物理层面的连接外，还应当结合空车与列车接续时间关系进行列车之间的空车配流.同时，网络中列车的旅行时间以及车站的技术作业时间具有不确定性，时间的波动会直接对供需网络的接续关系造成影响.因此，本文基于鲁棒优化理论对多车种、可替代条件下的空车调运问题进行了研究.

1 问题描述与建模

1.1 问题描述

供应站与需求站的车站技术作业时间以及站间旅行时间不确定性时，如何确定需求站的空车来源、类型与空车数量是鲁棒接续时间要求下空车调运的核心问题.模型中包含下述参数.

定义集合及索引：I、i分别为空车供应站集合和索引，i∈I；J、j分别为空车需求站集合及索引，j∈J；E、e分别为供应站内产生空车的到达列车集合及索引，e∈E；F、f分别为供应站发出的可挂运空车的列车集合及索引，f∈F；G、g分别为需求站内需使用到达空车装车的发出列车集合及索引，g∈G；η为实际的空车类型， χ 为考虑车种替代后按用途归类的空车类型，空车类型集合H包括平车（N）、棚车（P）和敞车（C），H={N,P,C} ，且 η , χ ∈H.

定义供应站相关变量：ci、ti分别为供应站i的等待车小时费用及车站技术作业时间；Sie,η、Sif分别为供应站i内第e列到达列车产生 η 型空车的数目及第f列发出列车的最大空车挂运数目；Aie、Lif分别为供应站i第e列到达列车的到达时刻及第f列发出列车的最晚编组时刻.

定义需求站相关变量：pj、cj和tj分别为需求站j的空车装车后产生收益、空车等待车小时费用及车站技术作业时间；Sjg,χ为空车需求站j第g列发出列车需要的 χ 型空车数量；Ljg为空车需求站j第g列发出列车的最晚编组时刻.

定义0-1变量：xi,e,f表示供应站i的第e列到达列车与供应站i的第f列发出列车间是否存在接续关系，xi,e,f= 1 为是，xi,e,f= 0 为否；yif,jg= 0 表示供应站i的第f列发出列车与需求站j的第g列发出列车间是否存在接续关系，yif,jg= 1 为是，yif,jg= 0 为否.

定义决策变量：di,e,f,η为供应站i的第e列到达列车为供应站i发出的第f列列车供应的η型空车的数量；dif,jg,χ为供应站i第f列发出列车为需求站j发出的第g列列车供应的χ型空车的数量；dif,jg,η为供应站i第f列发出列车为需求站j第g列发出列车供应的η型空车的数量.

另外定义了空车供应站i和空车需求站j间的空车输送费用cij及站间旅行时间tij.

1.2 名义模型构建

名义模型是将供应站与需求站车站技术作业时间以及站间旅行时间看作确定值时的空车调运模型.

1）目标函数

以空车调运效益最大化为目标函数，如式（1）所示，其中：等号右端第1项表示空车到达需求站后由需求站装车发出所产生收益；第2项表示空车调运时产生的路径消耗费用[7]；第3项表示空车在需求站的等待费用；第4项表示空车在供应站的等待费用.

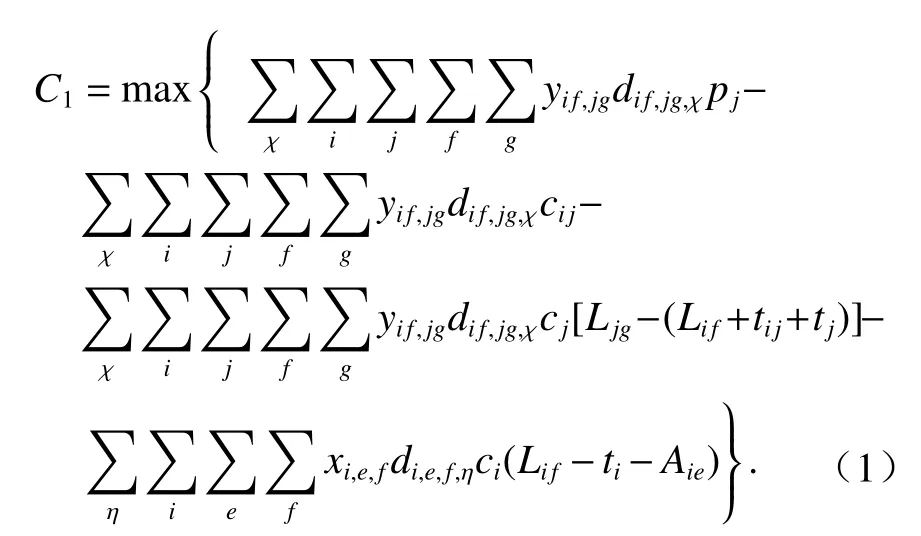
2）约束条件

式（2）表示供应站i的第e列到达列车给该站各发出列车f提供的η型空车总数不得超过第e列到达列车产生η型空车总数.

式（3）表示供应站i的各次到达列车e为该站第f列发出列车供应的空车总数不得超过第f列发出列车的最大空车挂运数目.

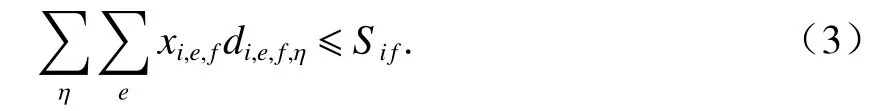
式（4）表示dif,jg,η中 η 型箱的数量等于其实际替换的各车型dif,jg,χ的数量总和.设Rη为 η 型箱可替代的车型集合，参考文献[8]，平车代替敞车有90%概率，棚车代替平车和敞车有75%的可能，敞车代替棚车有30%的可能，故有RN= {N,C}，RP= {N,P,C}，RC= {P,C}.

式（5）表示供应站i发出的第f列列车中挂运的各型空车均用于满足需求站的空车需求[9-10].

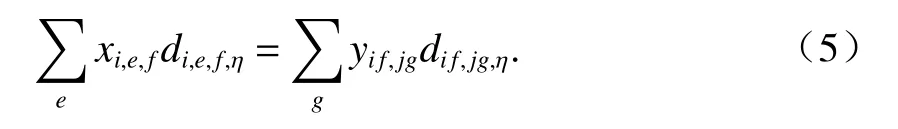
式（6）表示各供应站发出的列车为需求站j发出的第g列列车提供的χ型空车数量等于该列车对χ型空车的需求量.

式（7）表示列车间空车输送数量非负.

式（8）表示如果供应站i的第e列到达列车在供应站i完成相关技术作业后，到达调车场的时刻不晚于i站第f列发出列车的最晚编组时刻，则该组供应站到达列车与发出列车之间满足最小接续时间要求，即xi,e,f= 1，否则，xi,e,f= 0.供应站到达列车产生的空车来自重车卸车时，ti= (ti,dj+ti,zx) + (ti,jt+ti,zx) +(ti,xc+ti,zx)；到达列车本身挂有空车时，ti= (ti,dj+ti,zx) +(ti,jt+ti,zx)；其中：ti,dj、ti,zx、ti,jt和ti,xc分别为i站的到达技术作业时间标准、转线作业时间标准、解体作业时间标准（含推峰时间）及卸车作业时间标准.

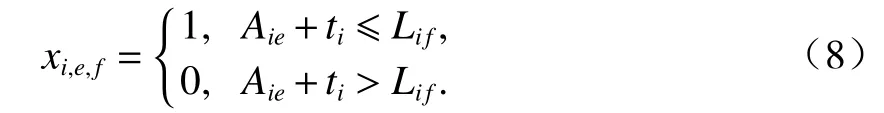
式（9）表示若供应站i发出的第f列列车在需求站j完成相关技术作业后，到达调车场的时刻不晚于j站发出第g列列车的最晚编组时刻，即yie,jg= 1，否则，yie,jg= 0.列车在需求站j的技术作业时间tj=(tj,dj+tj,zx) + (tj,jt+tj,zx) + (tj,zc+tj,zx)，其中：tj,dj、tj,zx、tj,jt、tj,zc分别为j站到达技术作业时间标准、转线作业时间标准、解体作业时间标准及装车作业的时间标准.

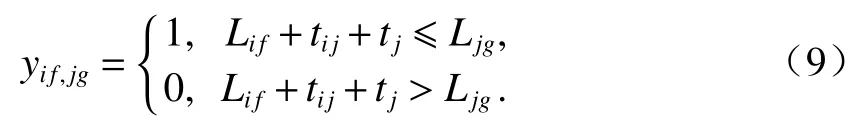
式（10）表示只有当供应站i第f列发出列车存在满足接续时间要求的空车来源时，即xi,e,f= 1时，才考虑该发出列车与需求站发出列车的接续关系.

为便于说明，本文定义了属于关系、连接关系和车流关系，如图1所示，图中：三角框为供应站，正方形框为需求站，圆圈为列车，后同.

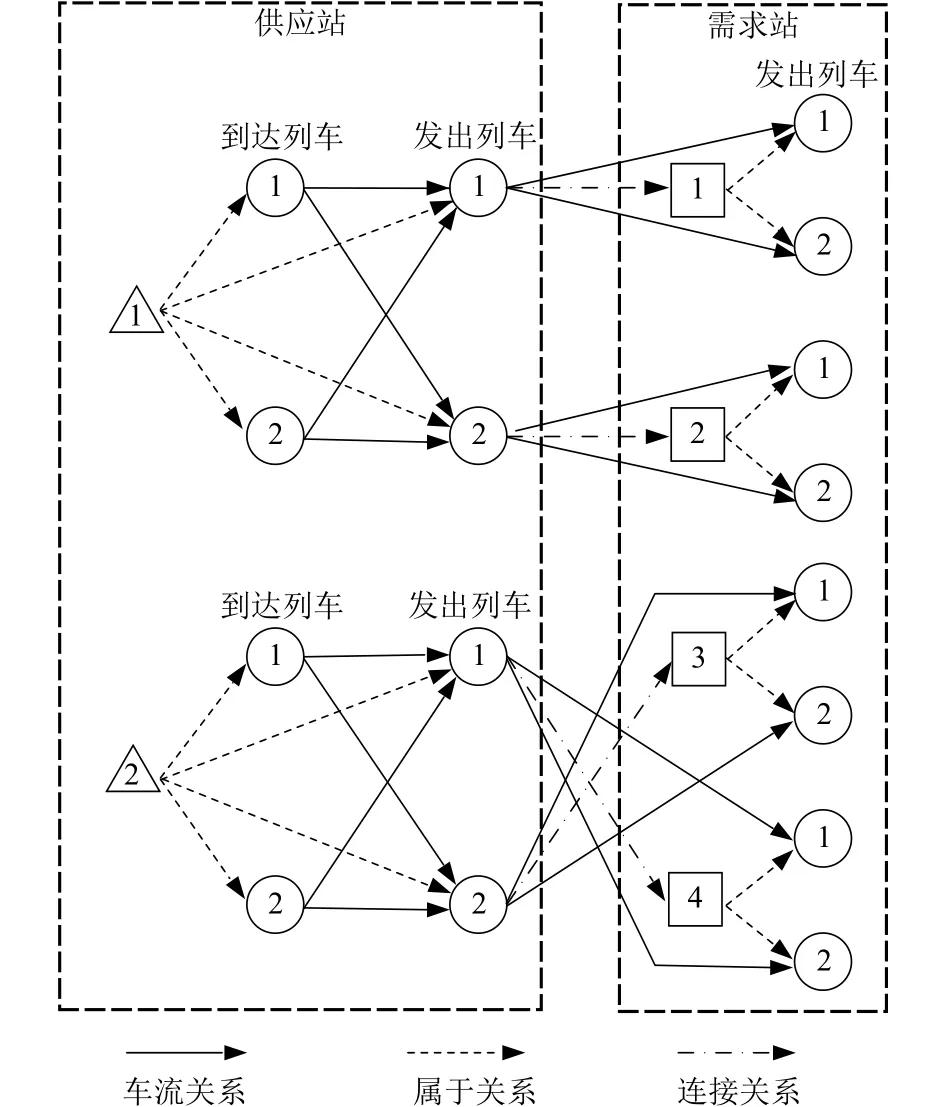
图1 空车调运网络Fig.1 Empty wagon allocation network

定义1属于关系指供应站到达列车e、发出列车f与供应站i之间的关系以及需求站发出列车g与需求站j之间的关系.

定义2连接关系为供应站发出的列车f与该列车到达的需求站j之间的关系，供应站发出的任一可挂运空车的列车有且只与一个需求站建立连接关系.

定义3车流关系是指当某一列车中的车辆可以成为另一列车中的车流来源时，两列列车之间存在的关系.车流关系可以定义为两部分：

1）供应站到达列车e与该站发出列车f之间的车流关系定义为第1阶段车流关系；

2）供应站发出的列车f与需求站发出的列车e之间的车流关系定义为第2阶段车流关系.

车流关系由约束条件式（8）～（10）确定.

1.3 鲁棒优化模型构建

实际运输中由于设备因素、环境因素和人为因素的影响，列车站间旅行时间以及车站技术作业时间是不确定的，若以固定的旅行时间和技术作业时间作为空车接续时间的判断依据，当接续条件Lif-(Aie+ti)≥0或Ljg-(Lif+tij+tj)≥0 ，但取值较小时，技术作业时间和旅行时间的波动可能使得既有的接续关系失效，导致求得方案不可行.因此，基于Dimitris等[11]提出的鲁棒优化理论建立了空车调运鲁棒优化模型.

1）目标函数

鲁棒优化模型的目标函数如式（12），约束关系如式（13）所示，结合波动程度与波动下限约束，式（12）中的C2如（14）所示，矩阵表达如式（15）所示.

式（13）、（15）中： δij、 δi、 δj、 θij、 θi、 θj为松弛系数；n为供应站数目 ；m为需求站数目；En为n×n的单 位 矩 阵 ；Zn为 元 素 全 为 1的 1 ×n矩 阵 ； δn=(δ1,δ2,···,δn)T； θn=(θ1,θ2,···,θn)T；Unm=(α11,α12,···,αnm)T；Vn=(β1,β2,···,βn)T；Wm=(γ1,γ2,···,γm)T.

证明一个矩阵为完全幺模矩阵的充分条件为：① 矩阵中元素仅包含 0、1、-1；② 矩阵每列最多两个非0元素；③ 矩阵的行可分划成两个子集，使得同列中两个非零元素符号相同时，对应的两行在不同的行子集中，当符号不同时，对应的两行在同一行子集中.易得：约束矩阵式（15）满足条件 ①、②，并且当矩阵行划分为(1,4)和(2,3,5,6)两个行子集时满足条件 ③，故该约束矩阵为完全幺模矩阵.结合完全幺模矩阵的性质，当 Γ1、 Γ2和 Γ3均取整数时，式（13）、（14）的最优解 α*、 β*、 λ*也为整数，因αij,βi,γj≥0，且 αij,βi, γj≤1 ，故其最优值取0或1.

2）约束条件

原约束条件中式（2）～（7）、（10）不变，式（8）、（9）分别变更为式（16）、（17）.

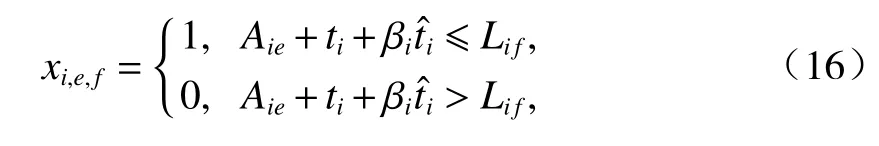
2 求解算法

2.1 名义模型求解算法

名义模型为非线性整数规划模型，求解困难，因此，求解前结合约束关系式(8) ～ (10)对模型进行简化.

以算例中的供应站3为例，为便于表示，此处仅保留三列供应站发出列车，变化前后网络结构如图2所示.与原网络相比，新网络中仅保留了xi,e,f=1 和yie,jg=1时所对应的决策变量di,e,f,η和dif,jg,η，进而去除模型中的约束条件式（8）～（10），转化为线性规划模型，可调用CPLEX进行求解.

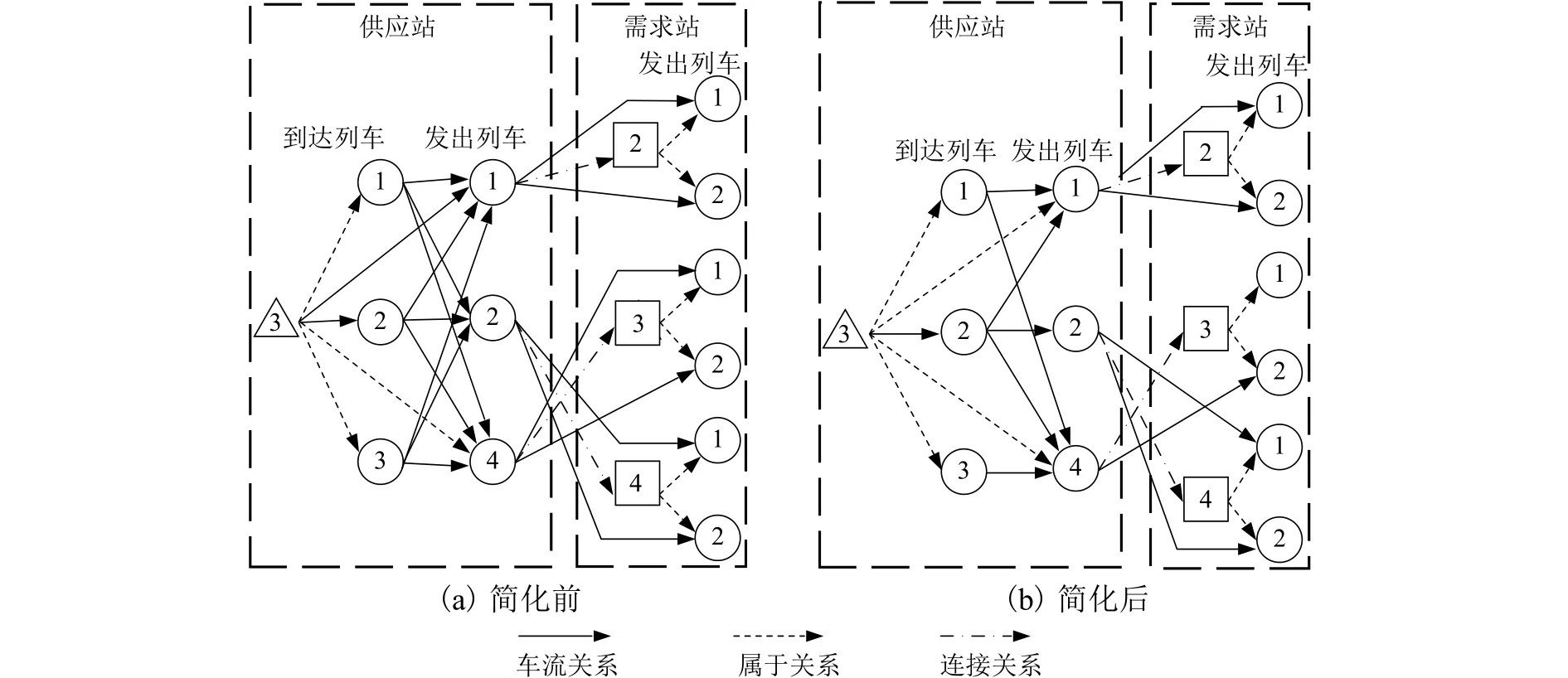
图2 简化前后网络图Fig.2 Network diagrams of pre- and post-simplification

2.2 鲁棒优化模型求解算法

鲁棒优化模型中引入了变量 αij、 βi、 γj，这些变量会导致供需网络中既有车流关系的变化，但对于每组 αij、 βi、 γj存在唯一的网络结构，求解时可以看作名义模型.

遍历满足约束的每组 αij、 βi、 γj是最准确的求解方法，但当 Γ1、 Γ2、 Γ3取值较高时模型的求解复杂度会剧增，导致求解困难.研究发现，只有当网络结构中的车流关系减少时，最优调运方案才可能改变，故设计下述步骤求解.求解时 Γ1、 Γ2、 Γ3和为已知值.

步骤1结合式(8)～(10)，得出固定出行时间下供需网络中存在的车流关系，令供应站i的第1阶段车流关系集合为 Ω1,i，供应站i的第2阶段车流关系集合为 Ω2,i，形式如下：

式中：Ω1,i中(e,f)表示i站第e列到达列车可以为i站第f列发出列车供应空车；Ω2,i中(f,j,g)表示i站发出的第f列列车可以为j站发出的第g列列车供应空车.

步骤 2令集合U、V、W中的各项元素均为 1，即所有的tij、ti、tj都存在波动，结合式（10）、（16）、（17），得出绝对鲁棒下的网络中存在的车流关系 Π1,i、Π2,i，形式同 Ω 1,i、 Ω 2,i.

步骤 3比较 Π 1,i、 Π 2,i和 Ω 1,i、 Ω 2,i中的车流关系数量，确定此时减少的车流关系.若 Π1,iΩ1,i，说明第1阶段车流关系发生了变化，若 Π2,iΩ2,i，说明第2阶段车流关系发生变化.假设此时减少的车流关系为 Ω1,1的 (1,1)， Ω1,2的 (1,2)， Ω2,2的(1,1,1)，Ω2,3的(2,2,1).

步骤4找出减少的车流关系中包含的供应站集合I1、需求站集合J1以及连接关系集合O，以步骤3中假设为例，减少的车流关系中包含的供应站为I1= {1,2,3}，包含的需求站为J1= {1,2}，包含的连接关系为O={(2,1),(3,2)}.

步骤5令集合U、V、W中的各项元素均为0.同时，根据供应站n1、需求站n2、连接关系n3及波动下限 Γ1、Γ2、Γ3，按下述方法确定 βi、 γj、 αij的取值：

1）若 Γ1≥|n1| （ |n1| 表示n1中元素个数，其余同），则令I1内各供应站的系数 βi为 1，以I1={1,2,3} 为例

即 β1=1 、 β2=1 、 β3=1 ；若 Γ1＜|I1| 则得到从I1中取Γ1个元素的全排列集合N1，令每组排列的系数为1；

2）针对 Γ2的调整方法同T1，当 Γ2＜|J1| 时，得到从J1中取 Γ2个元素的全排列集合N2；

3）若 Γ3≥|O| ，则令O中各元素的系数 αij=1 ，以步骤3中假设为例， α21=1 ， α32=1 ；否则，得到从O中取 Γ3个元素的全排列组合N3,令每组排列的系数为1.

步骤 6输入由N1、N2、N3中元素组成的 αij、 βi、γj排列，调用CPLEX求解各网络结构下的最佳效益值，取其中的最小值作为鲁棒解.

该算法在给定波动量tˆij、tˆi、tˆj的情况下，找出最劣网络结构较理想网络结构中减少的车流关系，以此为入手点找出波动下限 Γ1、 Γ2、 Γ3下最可能引起网络结构变化的 αij、 βi、 γj排列，避免了无效遍历，减少了求解时间.

3 模拟计算及结果分析

3.1 参数输入

以5个需求站和4个供应站构成的网络进行分析.供应站列车的到达时刻Aie、产生的各型空车数量Sie,η见表1.供应站发出列车f的最晚编组时刻Lif、发往需求站j和最大空车挂运数量Sif见表2.需求站发出列车g的最晚编组时刻Ljg及空车需求量Sjg,χ见表3.站间空车输送费用cij、名义旅行时间tij见表4.各车站等待车小时费用ci、cj，固定作业时间ti、tj，空车装车后的发送效益pj见表5.规划阶段起始时刻为 0，1 天为 1 440 min，表中负号对应前一天的时间.前一阶段残存空车也按照其实际列车到达情况加入供应站到达列车数据.

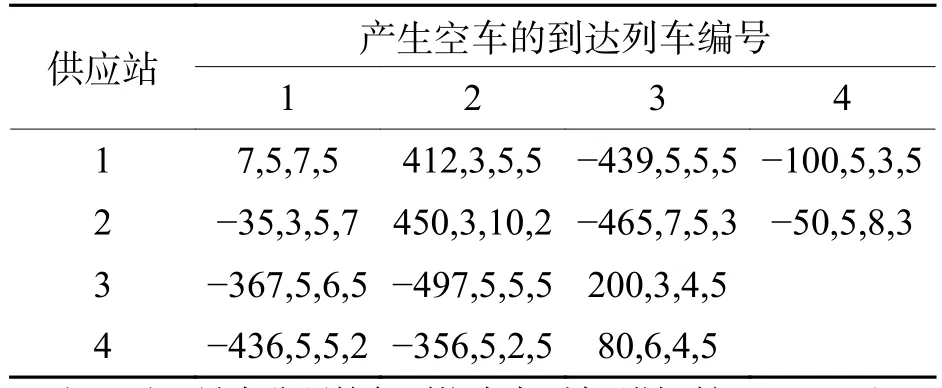
表1 供应站列车到达时刻及空车产生数量Tab.1 Time of train arrival and number of empty wagons produced in supply stations

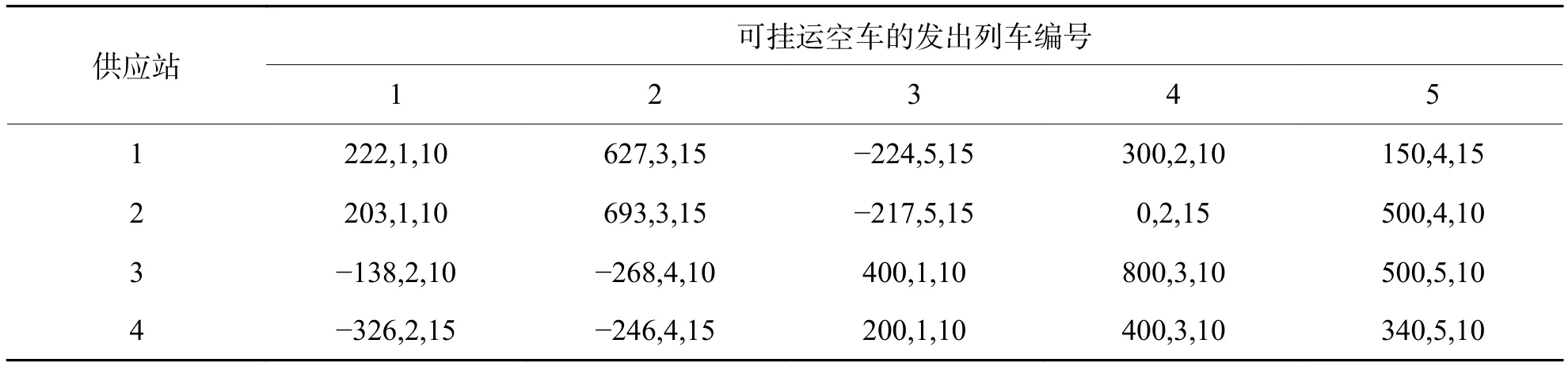
表2 供应站列车最晚编组时刻及最大空车挂运数量Tab.2 Train marshalling time limit and maximum number of empty wagons in supply stations

表3 需求站列车最晚编组时刻及所需空车数量Tab.3 Train marshalling time limit and number of empty trains required in demand stations

表4 站间空车输送费用及名义旅行时间Tab.4 Empty wagon transportation cost and nominal travel time between stations

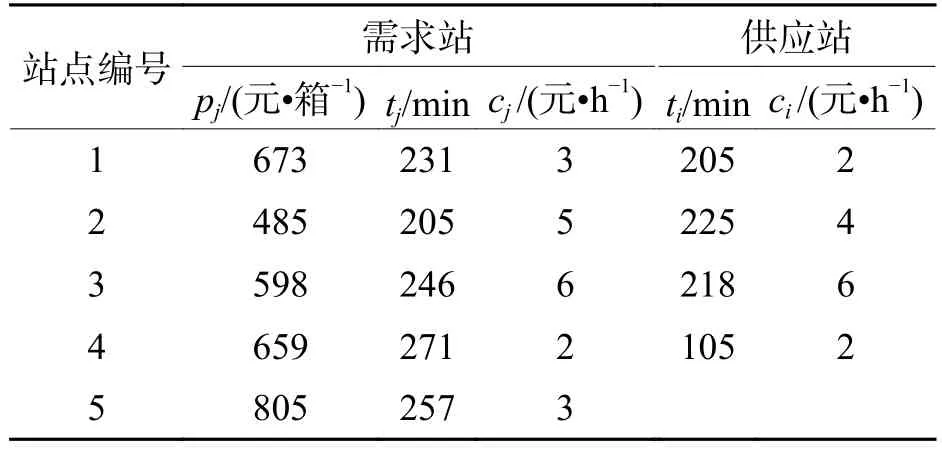
表5 车站参数数据Tab.5 Station parameter data

3.2 名义模型求解结果

通过MATLAB 2018a调用数学优化软件CPLEX编程求解，得到该供需网络下的最优空车匹配方案，供应站各发出列车挂运的空车来源见表6.各需求站发出列车的空车来源见表7.该网络下存在474个第1阶段车流关系，204个第2阶段车流关系，空车输送效益值为53 708元.

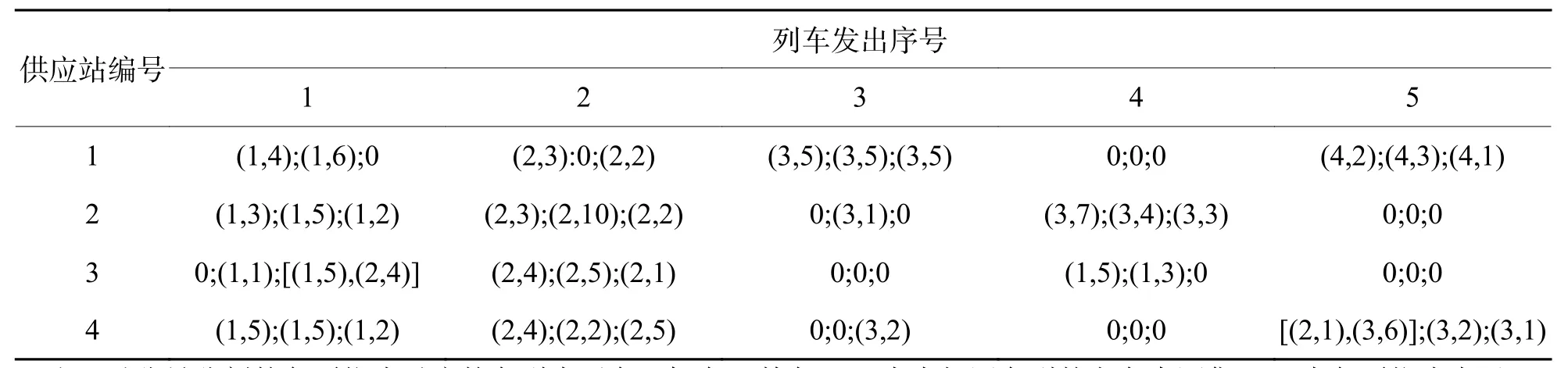
表6 供应站发出列车的空车来源Tab.6 Empty wagon source of trains leaving from supply stations

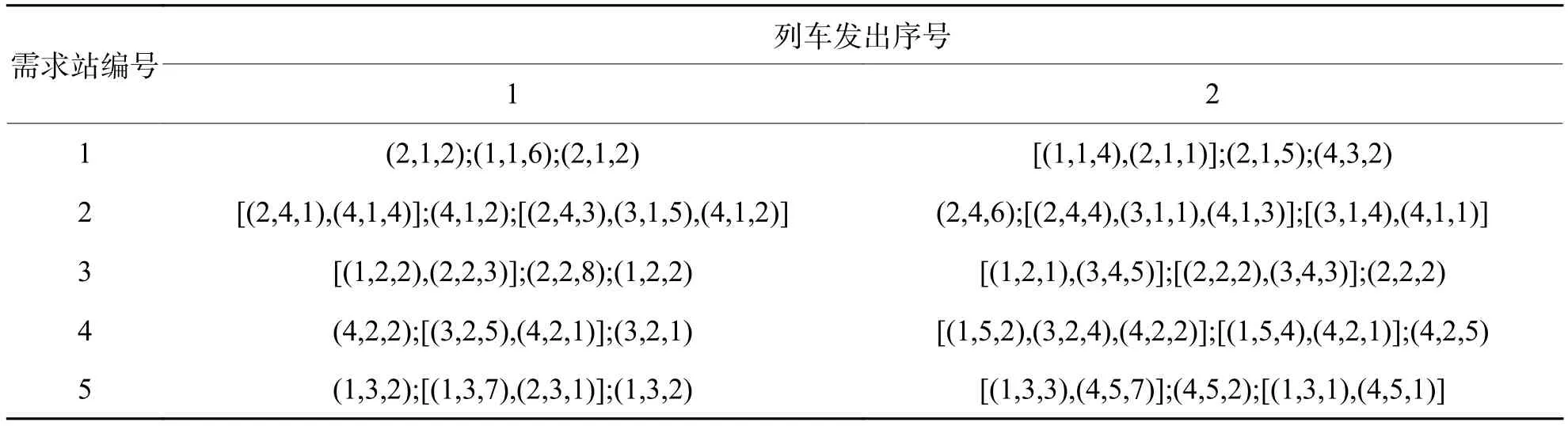
表7 需求站发出列车空车来源Tab.7 Empty wagon source of trains leaving from demand station

空车替代情况：需求站2发出的列车2中由列车(4,1,1)供应的1辆敞车为平车用作敞车.需求站4发出的列车2中由列车(1,5,4)供应的棚车中，有1辆为敞车用作棚车.需求站5发出的列车1中由列车(1,3,7)供应的棚车中，2辆为敞车用作棚车.

3.3 鲁棒优化模型分析

波动量和波动下限造成的网络结构变化可能导致无可行解，为保证可行解的存在对网络进行下述变化.

1）为各供应站增加一辆虚拟到达列车，该列车与供应站所有发出列车f均存在接续关系，且挂有充足的各类型空车；

2）任一供应站与所有需求站间均增加一列虚拟发出列车，该列车与需求站所有发出列车g均存在接续关系且发出列车的空车挂运能力充足；

3）当供应站发出列车空车来源为供应站虚拟到达列车时，供应站库存费用取较大常数，当需求站发出列车车流来源为供应站虚拟发出列车时，需求站发车效益为0.

4）求得最优解后，除去供应站虚拟到达列车和虚拟发出列车对应车流关系，结合式（1）求解实际效益，作为当前方案下的效益值.

3.3.1 单因素波动影响分析

模型中的不确定因素包括站间旅行时间、供应站及需求站作业时间3项.各因素的不确定程度由波动量和波动下限 Γ1、 Γ2、 Γ3共同决定，令不同波动下限下效益值随的变化即可看作效益值随波动率q1、q2、q3的变化.单因素波动导致效益值和网络结构的变化如图3所示.

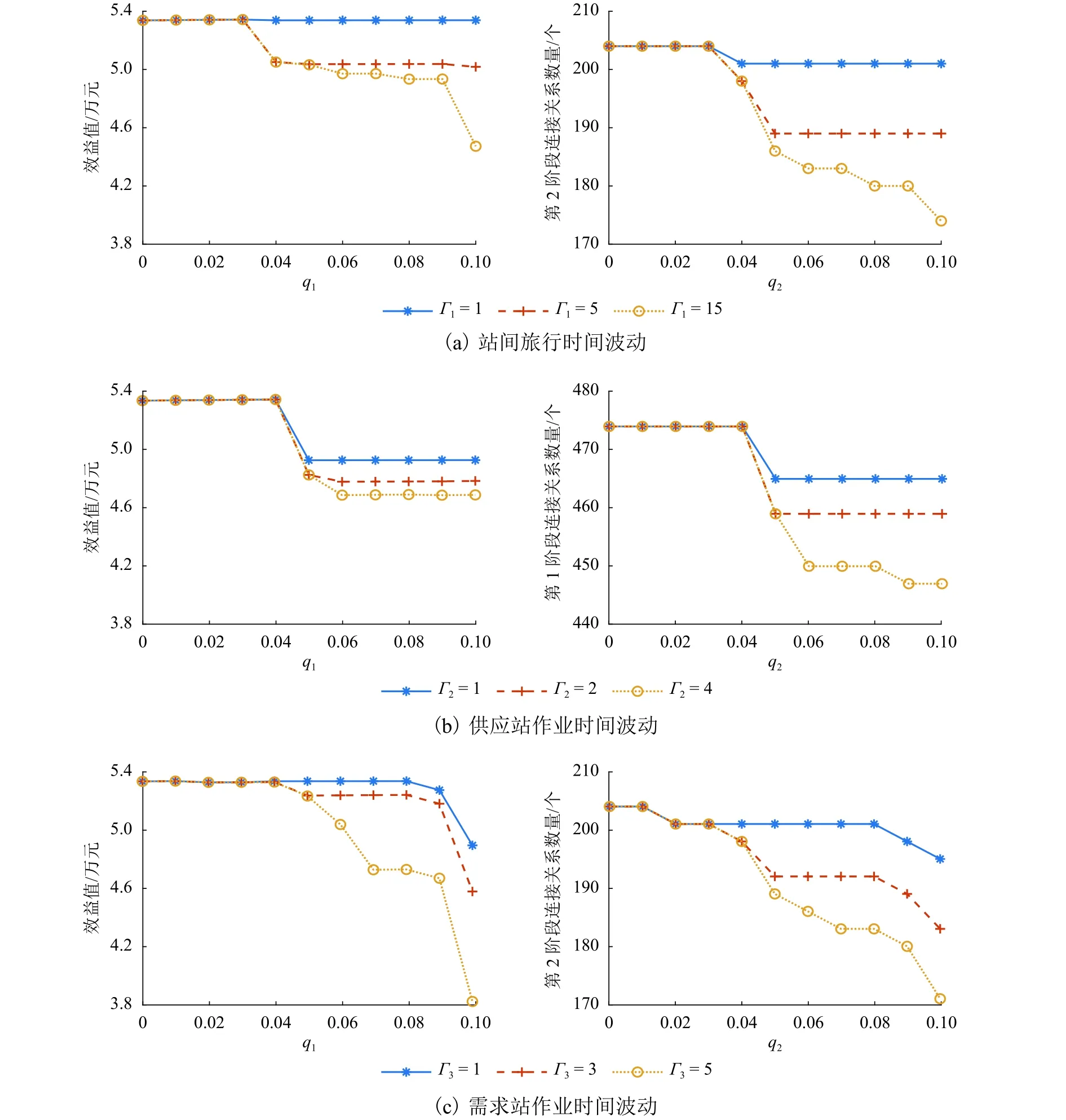
图3 单因素波动率影响分析Fig.3 Fluctuation influence analysis from single factor

由图3可知：

1）单因素的不确定性导致效益值出现较大变化时，必然伴随车流关系的变化.只有当减少的车流关系属于当前最优调运方案时效益值才会有较大变化.

2）相同波动率下效益值差距较大时，波动下限越大效益值越小.此时，相同波动率下的最优调运方案不同，波动下限越大，网络中存在车流关系越少，网络结构越劣，效益越小.

3）相同波动率下效益值很接近时，波动下限越大效益值越大.此时最优调运方案一致，波动下限越大，受到影响的作业或旅行时间越多，车辆的等待时间越小，效益值越大.

4）从单因素的绝对鲁棒性来看，波动率相同时，效益值越小则受波动率影响越大，故各因素对效益的影响程度为tj＞tij＞ti.

3.3.2 多因素波动率影响分析

给定 Γ1=15 ， Γ2=2 ， Γ3=3 ，q1 、q2 、q3 之间互动关系如图4.q2的大小决定第1阶段连接关系的数量，也决定了优化结果的上限.随着q2的增大，效益值整体波动幅度逐渐减小，q2不变时效益值随q1、q3的增大而减小.

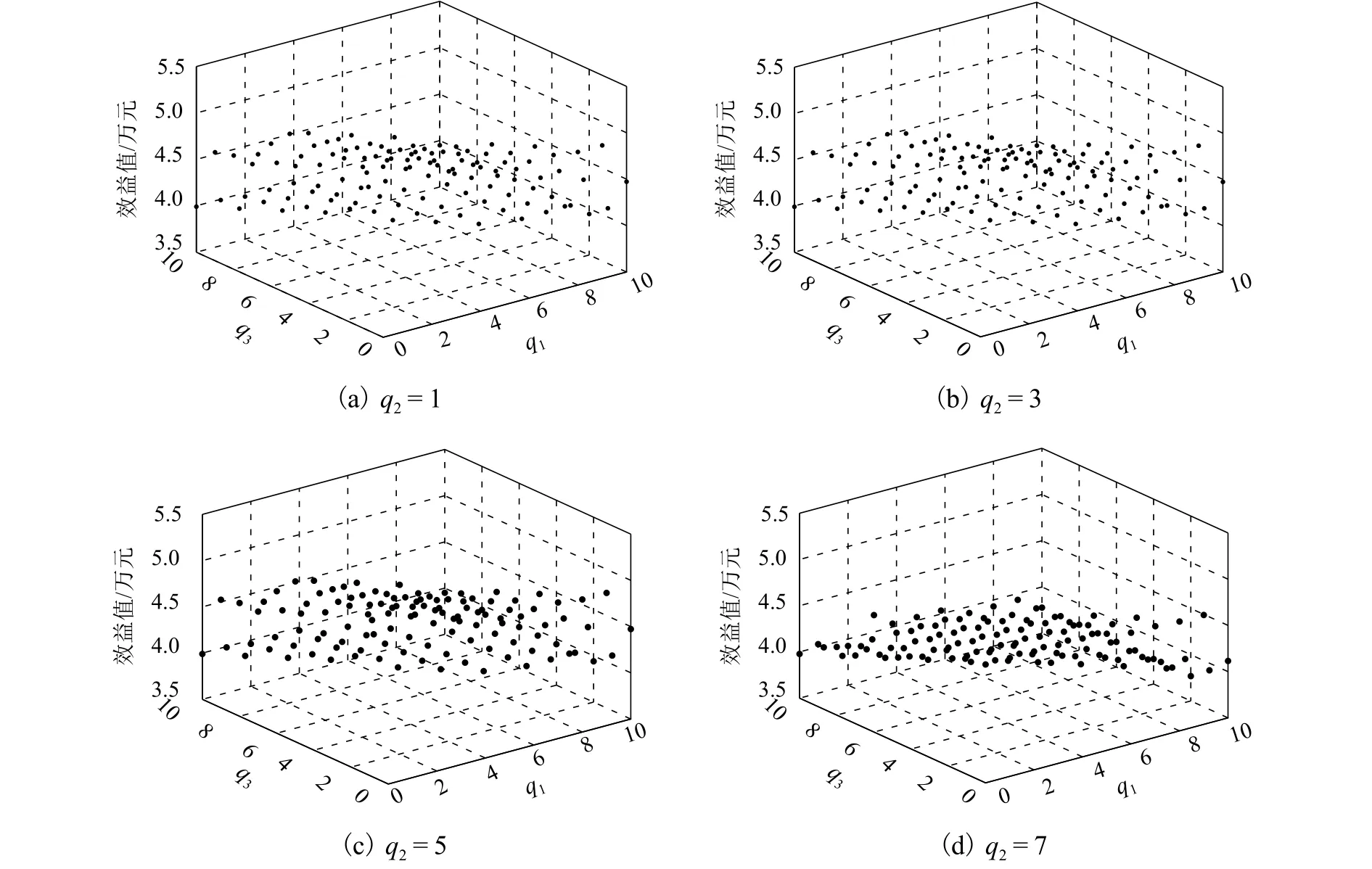
图4 多因素波动率影响分析Fig.4 Fluctuation influence analysis from multiple factors

3.3.3 波动下限影响分析

当q1=5% ，q2=4% ，q3=5% 时，不同Γ1、Γ2、Γ3下方案效益值如图5所示.

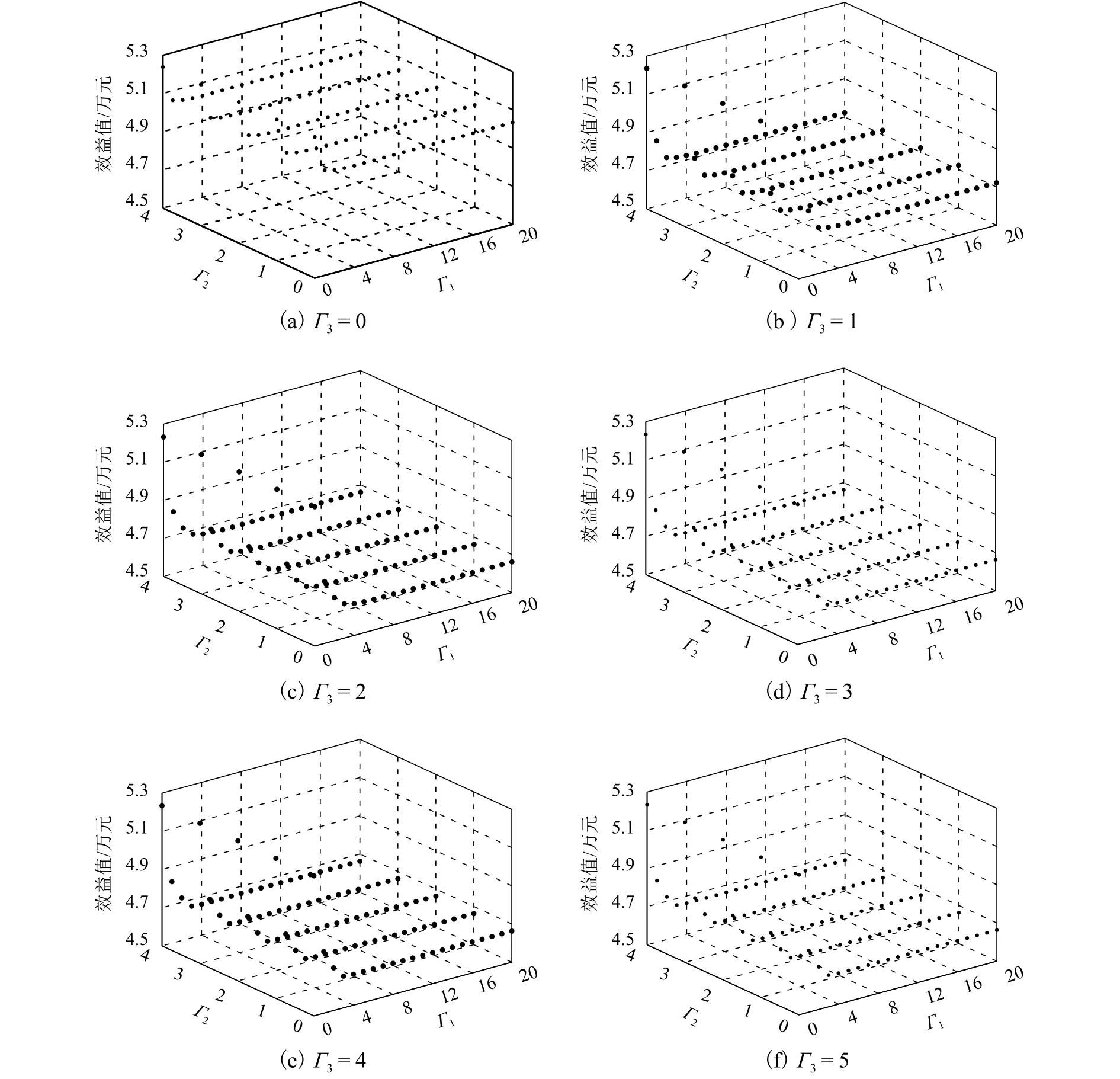
图5 波动下限影响分析Fig.5 Influence analysis of lower limit of fluctuation

1）站间旅行时间波动下限影响分析

Γ2、 Γ3取值相同， Γ1∈[0,2]时， Γ1对效益有显著影响，并且 Γ1越大效益越小.Γ1∈[3,20]时， Γ1对效益无显著影响， Γ1越大效益值越大.

2）供应站作业时间波动下限影响分析

Γ1、 Γ3取值相同， Γ2的取值对效益无较大影响，并且 Γ2越大效益值越大.

3）需求站作业时间波动下限影响分析

Γ1、Γ2取值相同，Γ3∈[0,1]时的效益明显大于 Γ3∈[2,5]时的效益，且效益与 Γ3的呈负相关.但当Γ3∈[2,5]时，虽然效益仍与 Γ3呈负相关，但无显著差异.

综上，供应站作业时间波动下限对效益值的影响最小.旅行时间波动下限和需求站作业时间波动下限取值较小时，它们对效益值有较大影响，并且二者间存在相互影响.

4 结 论

1）提出供应站到达列车、发出列车以及需求站发出列车间的空车接续时间关系判断方法，并据此分别建立了确定环境与不确定环境下的空车调运优化模型.

2）考虑构建模型的特征，将确定环境下的模型转化为了线性模型，并结合车流关系的变化是效益值变化的主要原因这一特点，设计了鲁棒优化模型的求解算法，求得了考虑车种替代的空车配流方案.

3）需求站技术作业时间波动率对效益值影响最大.供应站技术作业时间波动下限对效益值影响最小.方案效益值随方案鲁棒性的提高而下降.