“双软”顶底板薄煤层沿空留巷底鼓机理分析

张 帅，徐金海，李 冲

(1.中国矿业大学 矿业工程学院，江苏 徐州 221116；2.中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州 221116)

底鼓是由于掘进、回采、留巷及其他因素影响引起的围岩应力状态发生变化以及在维护过程中围岩性质的变化造成的[1]。目前，综放沿空巷道底鼓现象越来越突出，这类巷道的底鼓不仅造成巷道的破坏，对窄煤柱、巷旁充填体乃至整个巷道的稳定性也有重要影响，强烈的底鼓带来大量的维护和翻修工作，严重影响矿井正常的生产，大大增加了巷道的支护和维修费用[2-4]。由于巷道所处的地质条件、底板围岩性质和应力状态的不同，巷道底鼓的方式及机理也各不相同，一般可分为四类：挤压流动性底鼓、压曲褶皱性底鼓、剪切错动性底鼓、遇水膨胀性底鼓[5-7]。学者针对沿空留巷底鼓机理进行研究，康红普院士[8]指出岩层的压曲、扩容和膨胀是引起巷道底鼓的重要原因；柏建彪教授[9]提出底板岩性、水平应力对底鼓影响至关重要，采动巷道底鼓控制重点是加固破碎底板，增大其峰后强度和残余强度，以加固的方法实现改良底板岩性，同时控制水平应力对底鼓的影响；姜耀东教授[10]探讨了巷道底鼓的基本特征，分析了4种类型底鼓的机理及影响因素，提出了巷道底鼓控制技术；华心祝教授[11]建立深井大断面沿空留巷底板受力模型，利用最小势能原理对底板变形量进行计算和分析；徐营[12]指出沿空留巷底鼓原因是巷道底板在一次回采后发生破裂，底板破裂岩体随后在一次回采和二次回采采动应力的作用下发生峰后蠕变。

目前研究已对沿空留巷底鼓问题进行了初步探讨，但是对于薄煤层沿空留巷底鼓机理研究成果尚处于深化过程。因此，本文以赵宫能源煤矿1701工作面为研究背景，采用温克尔理论建立沿空留巷底板力学模型，揭示沿空留巷底鼓机理。

1 工程概况

1.1 煤层赋存

赵官能源煤矿1701工作面开采煤层为七煤层，该面构造形态为一宽缓的单斜构造，工作面煤层走向50°～75°，倾向正北，煤层倾角为3°～5°，较为平缓。煤层厚度1.05～1.20m，平均煤厚1.15m，厚度变化较稳定。

1.2 工作面布置

1701工作面位于-415m水平一采区东翼，东至F17断层保护煤柱，西到工业广场保护煤柱，南部为1701上工作面，北部为上一工作面采空区。1701工作面走向长1190m，倾向长162m，距地面垂深360.18～388.50m。工程实践过程中在1701上巷沿空留巷，并与一采区回风上山、运输上山相连，工作面布置如图1所示。

图1 工作面布置

1.3 巷道顶底板岩层岩性

1701工作面巷道直接顶为泥岩，平均厚度1.8m；基本顶为粉砂岩，平均厚度1.2m；老顶为细粒砂岩，平均厚度4.4m；直接底为泥岩，厚度为1.0～1.2m；老底为浅灰～灰色细砂岩，厚度为3.7m，煤层围岩如图2所示。

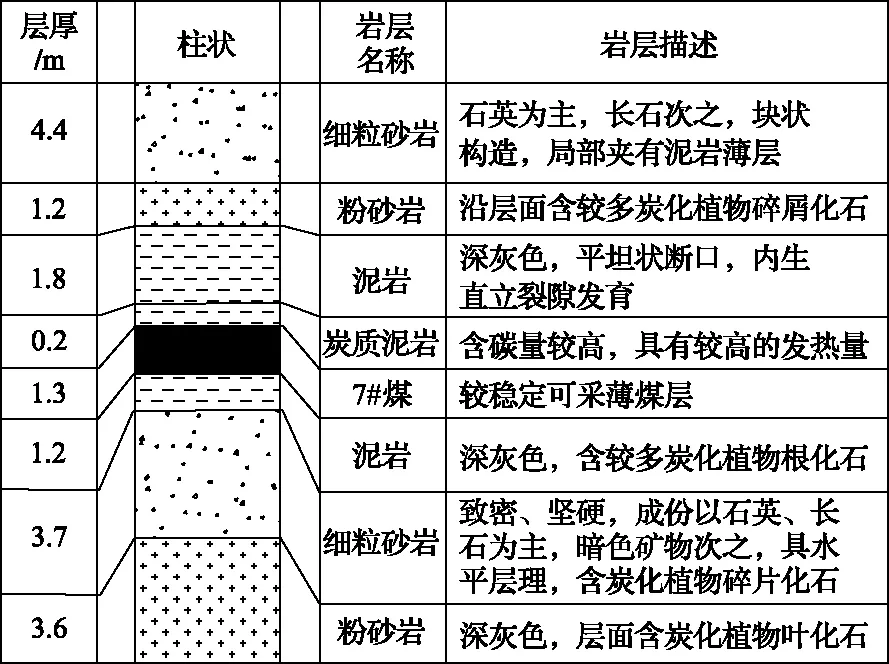
图2 煤层顶底板岩层柱状

由图2可知，7#煤层直接底为岩性较差的泥岩，在沿空留巷过程中无疑会加剧底鼓引起的巷道围岩变形。此外，巷道底板岩层中含有一定量的植物碎片化石，遇水具有一定的膨胀性，但是由于水文地质条件简单，顶底板含水层富水性较差，因而对巷道底鼓的影响程度较小。

1.4 沿空留巷支护方案

1701上巷支护方案采用“锚网+钢带”支护形式。顶板锚杆规格为∅18mm×2000mm的全螺纹钢等强锚杆，间排距800mm×800mm，巷帮锚杆规格为∅18mm×1800mm全螺纹等强锚杆，间距排800mm×900mm，巷道全断面铺网；沿空留巷采用原位留巷，巷旁充填体采用膏体充填，巷旁充填体宽1.5m，与煤层顶板接顶，高1.15m，在采空区侧人工垒砌宽为2.0m的矸石墙，具体布置如图3所示。

图3 沿空留巷初始方案(mm)

1.5 底鼓特征

现场观测发现，上巷顶帮支护密度及强度较大，底板无支护。滞后留巷一段时间，巷道出现底鼓。主要表现为：底板隆起，局部达到1m左右，严重影响了巷道的正常使用；部分巷旁支护体发生倾斜，在靠近顶板和底板的部位支护体发生剪切破坏；实体煤侧巷帮变形较小，未出现破损现象；顶板破坏程度小，较为完整。

2 沿空留巷底鼓力学模型

2.1 沿空留巷底鼓机制分析

根据关键层理论和沿空留巷覆岩移动规律可知[13-15]，工作面推过后，关键顶板在靠近采空区侧断裂形成砌体梁结构，此时，侧向集中应力向实体煤侧转移，围岩应力发生二次分布，并出现集中应力。

随着关键块的回转、下沉，巷旁充填体和实体煤承受的载荷迅速增大，巷道的基角处会产生强烈的应力集中现象。所以底板岩层的两端最容易发生破坏。当基角处破坏以后，基角基本失去了垂直向上的承载能力。因而，当巷道两帮发生相对移近时，强度较弱的底板分层在巷旁充填体与实体煤的挤压以及底板应力的作用下发生压曲变形，最终底板隆起形成底鼓。沿空留巷底鼓破坏形式如图4所示。

图4 沿空留巷底鼓破坏

2.2 沿空留巷受力分析

根据上述分析，可建立沿空留巷底板受力分析如图5所示，其中k1为工作面超前支撑压力的应力集中系数；k2为侧向支撑压力和超前支撑压力叠加形成的高支撑压力区的应力集中系数；k3巷旁充填体应力集中系数；γ为上覆岩层平均容重，N/m3；H为采深，m。

图5 沿空留巷底板受力分析

为了便于研究沿空留巷底鼓力学行为又不失其本质，取巷道左侧形成侧向支撑压力和超前支撑压力叠加形成的高支撑压力区和右侧的巷旁充填体应力集中区，都将其简化为均布载荷。基本底对直接顶的力简化为弹性地基，如图6所示，图中x1为沿空留巷宽度，m；x2为巷旁充填体应力集中区宽度，m；x3为高支撑压力区宽度，m。

图6 弹性地基底板沿空留巷力学模型

根据弹性地基温克尔假设[16-18]，地基表面任一点的沉降量和该点单位面积上所受压力成正比，即：

q=kω(x)

(1)

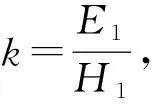
根据弹性地基岩梁理论，顶板挠度ω(x)与顶板岩梁所受载荷q之间应满足地基梁挠曲线基本微分方程：

式中，E为弹性模量，MPa；I为截面惯性矩，m4。

顶板岩梁的挠曲线微分方程为：

对于式(3)，整理可得：

方程(3)的齐次方程为：

齐次方程(6)的通解为：

ω1(x)=e-αx(A1cosαx+A2sinαx)+

eαx(A3cosαx+A4sinαx)

(8)

又因为非齐次方程(6)的一个特解为：

因此，非齐次方程(6)的通解为：

ω1(x)=e-αx(A1cosαx+A2sinαx)+

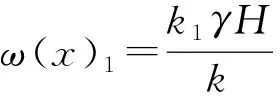
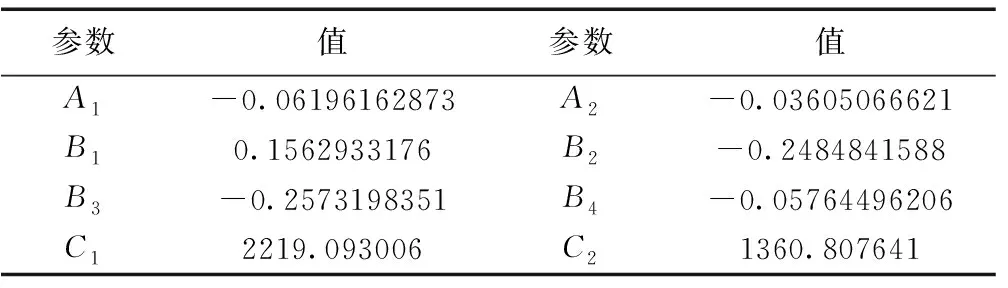
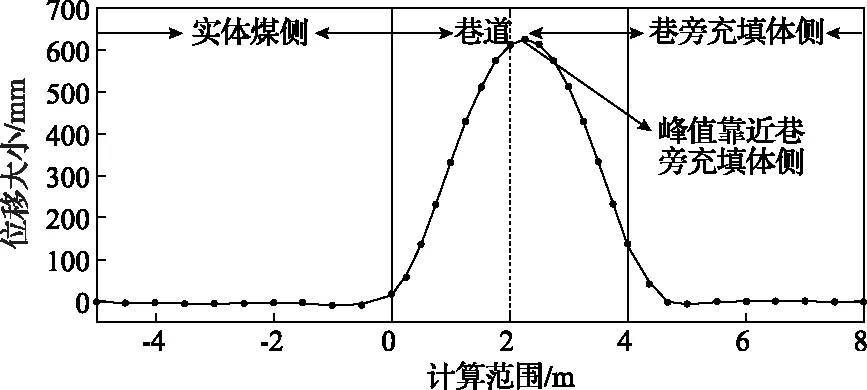
同理，当x2

当0

综上所述，顶板梁的挠曲线微分方程为：

梁的挠曲线求出后，任意截面的转角θ(x)、弯矩M(x)、剪力Q(x)可由下列方程求出：

考虑边界挠曲值和挠曲线方程连续性条件：

可解得参数A1、A2、B1、B2、B3、B4、C1、C2，由于参数形式过于复杂，这里不具体予以给出。将解得参数带入式(13)中即可得顶板岩梁的挠曲线方程。

3 工程计算实例

3.1 计算参数的确定

根据1701上巷采用巷旁膏体充填沿空留巷技术现场地质条件。参数选取如下：

工作面直接底厚度1.2m，基本底厚度H1=3.7m，煤层埋深为400m，取q0=10MPa。根据实验室实测结果可得，直接底和基本底岩层的弹性模量分别为E=0.5GPa，E1=15GPa；实体煤侧应力集中系数k2为2～2.5，取k2=2.5，膏体充填体应力集中系数k3为0.25～0.45，考虑到膏体充填体的长度较短，计算范围选取到采空区压实区10m，取k3=0.8。

3.2 计算结果分析

根据图6所示的力学模型，将相关参数带入，根据求解条件(15)，可以求得沿空留巷底板挠曲线方程。由于方程形式复杂，给出主要参数见表1，将参数带入式(13)可得底板挠曲线方程ω1(x)、ω2(x)和ω3(x)。

表1 沿空留巷底板挠曲线方程主要参数

将挠曲线方程ω1(x)、ω2(x)和ω3(x)用软件成图，得出巷旁膏体充填沿空留巷底板位移曲线如图7所示。

图7 沿空留巷底板位移曲线

由图7可知，实体煤与巷旁支护体侧底板变形接近零，巷道区域底板变形呈现为“抛物线”特征，具有非正对称现象，底鼓最大变形处位于靠近巷旁支护体侧，最大值为628mm。分析原因可知由于临空工作面采动影响，巷道底鼓靠近采空区侧变形更为剧烈。

3.3 模型验证

对1701上巷底板变形进行观测，沿空留巷底板100d变形曲线如图8所示。

图8 沿空留巷底板变形实测曲线

由图8可知，1701上巷底板变形随着时间的增加而变大，在初期50d内，巷道底鼓变形速率较快，达到13.3mm/d；后期达到50d之后，巷道底鼓变形较为缓和，变形速率为0.9mm/d，100d后变形最大值为645mm，理论模型最大值与实测最大值误差为2.6%。

4 结 论

1)采用Winker弹性地基建立了沿空留巷底板底鼓力学模型，给出了底板底鼓变形挠度方程解析解。

2)理论计算结果表明实体煤与巷旁支护体侧底板变形接近零，巷道区域底板变形呈现为“抛物线”特征，具有非正对称现象，底鼓最大变形处位于靠近巷旁支护体侧，最大值为628mm。

3)1701上巷底板变形随着时间的增加而变大，在初期50d内，巷道底鼓变形速率较快，达到13.3mm/d；后期达到50d之后，巷道底鼓变形较为缓和，变形速率为0.9mm/d，100d后变形最大值为645mm，理论模型最大值与实测最大值误差为2.6%。