基于改进卡尔曼滤波的结构损伤识别方法研究
2022-02-10沈皓,常军
沈 皓,常 军
(苏州科技大学 土木工程学院,江苏 苏州 215011)
卡尔曼滤波算法是近几十年发展起来的一种行之有效的结构损伤识别方法。卡尔曼滤波算法是一种基于最小方差准则的线性无偏估计方法,能够实现有限观测量下的结构状态的实时估计[1]。对于土木工程结构的卡尔曼滤波算法损伤识别,国内外学者已经做过很多研究。王坚等[2]提出了扩展卡尔曼滤波,解决了一般的线性问题,但原始状态误差较大或非线性程度较高时,会严重影响滤波精度;宝志雯等[3-4]提出了基于推广卡尔曼滤波算法的剪切型结构模型的参数识别方法,实现了结构刚度和阻尼的识别。周丽等[5]提出了基于自适应卡尔曼滤波的识别方法,并对剪切线性模型实现了刚度和阻尼的识别。
在系统识别方面,已经有很多时域分析方法在相应文献中提出,比如:最小二乘估计[6],卡尔曼滤波[7],序列非线性最小二乘法等[8]。Julier[9]提出了无迹卡尔曼滤波,采用Sigma点近似其均值与方差,简化了计算,但带来的问题是对高于3维状态向量估计时,其精度达不到要求;王路[10]提出了自适应迭代无迹卡尔曼滤波,其实现了自动迭代的功能,不需要人工设置迭代,可还是不能解决高维的非线性问题,精度不够理想;Arasaratnam等[11]提出的容积卡尔曼滤波(Cubature Kalman Filter,CKF),其核心思想是对于非线性高斯系统,利用数值积分理论,保证任意非线性高斯状态的后验均值和方差可以近似为三阶多项式,但由于初始误差较大,降低了CKF对其估计的精度;为了提高CKF运行速度,穆静[12]提出了迭代容积卡尔曼滤波(Iterated CKF,CKF),但其不具有自动迭代的功能,需要人工设定迭代的次数。为此,本文借鉴遗忘因子的滤波算法和AIUKF的思想,把遗忘因子与自适应迭代容积卡尔曼滤波(Adaptive Iteration CKF,AICKF)相结合,这样既可以起到遗忘因子的作用,减少历史数据对滤波结果的影响,又可以提高滤波算法本身的准确性和处理非线性问题的能力。
1 KF算法的结构损伤识别
1.1 离散状态空间方程和KF算法
线性系统的结构动力学方程可写成连续的状态空间方程。如式(1)和(2)所示。

KF算法是无偏移递归算法,可最优估计未知状态向量。经典KF算法为第k步时估计先验状态向量

第k步时刻的状态向量

先验误差方差

状态向量估计均方差

卡尔曼滤波增益

在经典KF算法中,非线性动态系统中过程噪声协方差矩阵Q,在实际中往往很难准确获得,而导致滤波器发散;滤波算法本身精度不高,会降低处理问题的能力。因此本文借鉴遗忘算法因子的滤波算法与AICKF相结合,这样既可以发挥遗忘因子的作用,减少历史数据对滤波结果的影响避免发散,又可以提高滤波精度和处理非线性问题的能力。
2 改进后KF算法结构损伤识别
2.1 AICKF算法
借鉴AIUKF算法的思想,在CKF基础上加入自适应迭代,在滤波算法上CKF精度就高于UKF,在加入自适应迭代后一方面迭代再次提高了滤波的精度,另一方面自适应省去了人工去设置迭代的问题。
考虑如下离散时间非线性动态系统

式中,xk为系统状态向量;zk为量测值。假设过程噪声wk-1和量测噪声vk相互独立,是均值为零,协方差分别为Qk-1和Rk的高斯白噪声。
容积卡尔曼滤波算法首先计算加权函数为标准正态分布密度的积分的基本容积点和对应的权值

m为系统的状态维数;ζj为第j个容积点;基本容积点按照下列方式产生,记n维单位向量为e=[1,0,…,0]T,使用[1]表示对的元素进行全排列和改变元素符号产生的点集,称为完整全对称点集,[1]j表示点集中[1]的第j个点;wj为对应点的权值。
2.2 遗忘因子的计算
遗忘因子[13-14]是为了限制滤波器的长度,让滤波值中的历史数据占的权重变小,新数据权重变大。

2.3 遗忘因子和AICKF结合的滤波算法
该算法的不同之处在于方差预测加入遗忘因子,即

这就意味着随着过程噪声协方差矩阵不准确时,加入遗忘因子不会对预测协方差产生较大影响,遗忘因子降低了历史数据对滤波结果的影响,增加了当前测量值在估计中的比例,提高了滤波精度[15-16]。具体算法步骤如下。
(1)初始化。初始化公式

(2)时间更新。首先,计算容积点及经非线性状态方程传播的容积点

式中:Sk-1=chol(Pk-1),chol()表示矩阵的乔列斯基分解。
然后,计算状态和方差预测,见下式

(3)计算容积点经量测方程的传递值和测量值。见下式。

(4)判断是否迭代。计算出预测值与实际观测值的适应度函数,体积点的传递值与实际观测值的适应度函数,并根据适应度函数的比值确定采样点与目标真实估计值的偏差,从而自适应确定是否进行迭代重采样。具体步骤,首先是定义适应度函数,预测测量值与实际观测值的适应度函数为

容积点传递值与实际观测值的适度函数为

适应度函数比

其中:zk为实际观测值;z^k为预测测量值;Zj,k为容积点传递值;Rk为观测噪声方差。
然后,判断是否迭代数据。
(5)若ρ<1,表示采样点有效逼近真实估计,则不进行迭代;接着往下计算量测更新。首先,计算新息方差和协方差
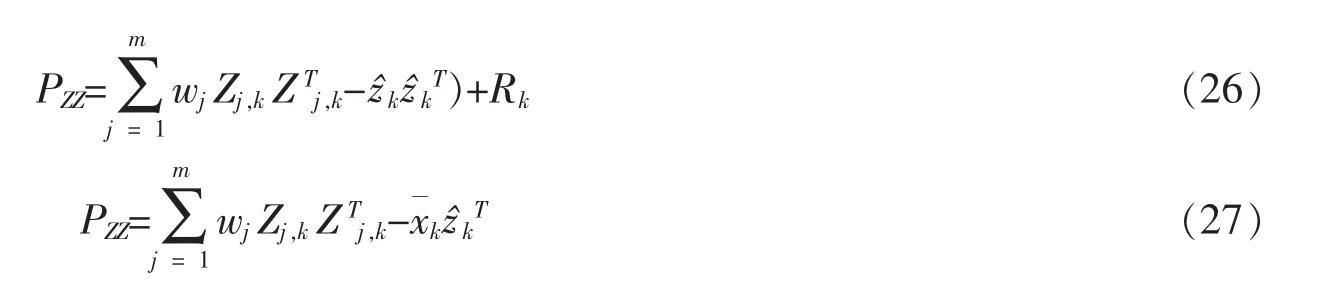
然后,计算增益。见下式

最后,计算系统的状态更新和协方差更新。见下式


(6)若ρ≥1,表示采样点与真实估计偏差较大,则进行迭代,步骤如下。
第二,重新时间更新。
第四,重新量测更新。
设迭代终止时的迭代次数为N,则k时刻的状态估计与协方差估计为
3 数值模拟分析
采用简支梁为数值算例验证所提方法的有效性和可靠性。该简支梁共20个单元,每个单元长1 m,梁截面尺寸0.5 m×1 m,结构的弹性模量2×107Pa,泊松比0.2,密度2 500 kg/m3。利用有限元分析软件ABAQUS建立了相应的有限元模型。通过降低单元刚度来模拟结构损伤状况,简支梁模型如图1所示。

图1 简支梁模型
对各节点输入不同的高斯白噪声,模拟环境激励。激励频率为500 Hz,激励时长20 s。每个单元的初始刚度为103 136 N/m。首先模拟单元3处发生损伤,刚度损伤5%,损伤后刚度值为97 980 N/m。考虑噪声影响,以白噪声激励模拟随机荷载,作用各节点,取噪声水平5%。图2是以上述工况为例,得到3号节点的加速度响应信号;图3是3号单元KF刚度识别曲线;图4是改进后KF刚度识别曲线。

图2 3号节点的加速度响应
从图3可看出,简支梁模型发生损伤时,传统卡尔曼滤波算法对损伤状况较为敏感,能够有效识别其损伤。图4表明改进后的卡尔曼滤波识别损伤结果。通过图3和图4的比较能够很直观的看出改进后的卡尔曼滤波识别值能够快速且稳定地收敛到真实值。表1是选取简支梁的部分单元参数识别结果对比。可以看出改进后的卡尔曼滤波误差值普遍降低了2%左右,说明改进后的卡尔曼滤波更能够准确有效的识别损伤。

表1 简支梁参数识别结果对比

图3 3号单元KF刚度识别曲线

图4 3号单元改进后KF刚度识别曲线
图5是噪声下刚度收敛时程曲线。从图5可以看出,改进后的卡尔曼滤波相比于传统的卡尔曼滤波的刚度识别曲线能够更快,更稳定的收敛到真实值。表2可以看出改进后的卡尔曼滤波算法在5%噪声水平时,刚度参数识别误差为1%左右,相比于传统卡尔曼滤波误差降低了5%,说明改进后的卡尔曼滤波对于结构损伤识别具有较强的抗噪性能。

表2 噪声下简支梁参数识别结果对比

图5 噪声下刚度收敛时程曲线
为了研究改进后的卡尔曼滤波不仅能识别单点损伤,还能识别多点损伤,假定单元2和单元4模拟损伤,模拟刚度下降10%,刚度值和为92 822 N/m,取噪声水平为5%。
表3是多点损伤简支梁结构参数识别结果。从表3可以不难看出,简支梁模型发生两点损伤时,改进后的卡尔曼滤波识别精度相比于传统的卡尔曼滤波识别能力更强,它能够有效地提取结构的损伤信号,进而准确的识别结构损伤状况,说明改进后的卡尔曼滤波具有多点损伤识别的能力。

表3 多点损伤简支梁结构参数识别结果
4 结论
(1)新改进的算法与传统的卡尔曼滤波算法相比较,通过数值模拟的简支梁进行参数识别,结果表明能够更加精确的识别结构构件的刚度进而诊断结构损伤位置和程度效果。
(2)通过上述数据结果表明该方法还可以有效减少误差,提高滤波精度。数值模拟结果表明该方法可以排除噪声因素的干扰,识别结构损伤发生的部位和程度,具有较好的抗噪性。
