小行星动能防御精确相对导航与制导方法研究

普渝皓，程实，陈杨*

(1.航天科工空间工程发展有限公司，北京100854；2.中国航天科工集团二院研究生院，北京100854)

1 引言

近地小行星对地球的威胁持续存在，特别是大量未发现编目的近地小行星对地球持续造成严重突发撞击威胁。从历史情况看，直径1km以上小行星撞击地球概率较低且短期内难以有效防御，直径10m以下小行星危害较小无需针对性进行防御，因此监测预警的重点目标为直径10m至1km的近地小行星。进一步考虑工程可行性、应对必要性等因素，防御任务重点为直径十米级至百米级的小行星。近年来，小行星防御技术成为研究热点，其中任务末段的相对导航技术与制导技术是关键技术[1]。

“双小行星重定向测试”(Double Asteroid Redirection Test, DART)任务于北京时间2022年9月27日，对Didymos双小行星系统中直径160m的次星Didymos B进行动能防御，仿真命中点距瞄准点约15m[2]，实际命中点距离图像中心17m。根据公开报道，DART任务主飞行器经过深空机动与多次中制导修正，满足中末交接班条件后，进入末制导阶段，在此阶段使用源于比例引导的制导律，制导算法使用扩展卡尔曼滤波(Extended Kalman Filter, EKF)对交会时刻的投影脱靶量进行估计[3]。滤波器的观测量是由图像解算出的惯性坐标下的视线角，并且假设任务飞行器与目标小行星之间无相对加速度。根据投影脱靶量大小进行修正，在交会前5min进行连续修正，并在交会前2min停控，准确命中目标小行星。面对目标尺寸更小、目标轨道预报精度更低、交会精度要求更高的任务场景，上述方法还有改进的空间。

首先，考虑提升滤波算法的精度。以视线角为观测量的相对导航系统是典型的非线性系统。EKF算法在线性化过程中忽略了非线性函数泰勒级数展开的二阶及以上的高阶项。在初始误差较大的情况下，特别是在目标轨道预报精度较低的情况下，有可能引入较大的线性化误差。无迹卡尔曼(Unscented Kalman Filter, UKF)算法不需要对状态方程和观测方程线性化，没有对模型高阶项的截断误差，可以获得比EKF更好的估计精度和滤波稳定性[4]。EKF和UKF算法均需要已知系统噪声和观测噪声的统计特性。噪声统计特性的偏差将导致滤波精度下降甚至导致滤波发散。为了克服这一问题，需要引入在线估计噪声统计特性和修正滤波增益的自适应滤波技术，如基于协方差匹配的自适应滤波[5]、基于极大似然方法的自适应滤波[6,7]和基于模糊逻辑的自适应滤波[8,9]等。

其次，考虑提升制导指令的计算精度。在公开文献中，DART任务在进行投影脱靶量估计时，忽略了相对加速度对制导精度的影响[2]。根据Lorenzo F的研究表明，DART任务在四体动力学环境下引起的轨道误差均值为238m，目标轨道不确定性引起的平均轨道误差为10m[10]。因此，为应对更小尺寸小行星的更高精度的防御场景，在投影脱靶量的估计时，需要考虑复杂引力环境产生的相对加速度。

本文首先以B平面坐标系作为相对导航坐标系，并给出该坐标系下的自主相对导航系统模型。其次将适用于线性系统的Sage-Husa噪声估计器推广到非线性系统，结合UKF算法得到一种自适应无迹卡尔曼(Adaptive Unscented Kalman Filter, AUKF)滤波器，并引入协方差匹配的思想，进一步提高滤波的快速性和稳定性。在投影脱靶量的估计计算中，考虑复杂引力环境下的影响，提出一种利用投影脱靶量直接计算制导指令的制导方法。最后以具有潜在威胁的小行星Bennu为目标，设计典型任务场景并生成飞行数据，对本文提出的模型及算法进行仿真验证。

2 自主相对导航方法

2.1 系统模型

2.1.1相对导航坐标系

本文考虑单目仅测角相对导航系统，以目标天体的俯仰角和方位角为观测量。任务末段飞行器相对目标天体的位置矢量和速度矢量夹角很小，甚至重合，沿视线方向的信息无法通过连续观测获得。若在J2000日心黄道坐标系中描述状态方程，视线方向距离无法估计的特性将反映到三个惯性坐标轴上，导致三轴的位置估计均不可信，无法保证三轴的位置信息的估计精度。因此，需要将沿视线方向的距离独立出来，提高垂直于视线方向的估计置信度。

B平面坐标系是根据任务飞行器相对目标天体进入渐近线方向定义的参考坐标系，如图1所示，其数学定义为：以目标天体为中心原点，S轴为进入轨道双曲线渐近线的方向矢量，某参考方向矢量记为N，S与N叉乘作为T轴，R轴由S轴和T轴按右手螺旋法则确定。在本文中，S矢量方向可选为初始时刻任务飞行器相对目标天体的速度V∞的方向。取N为任务飞行器轨道平面的法线。即：

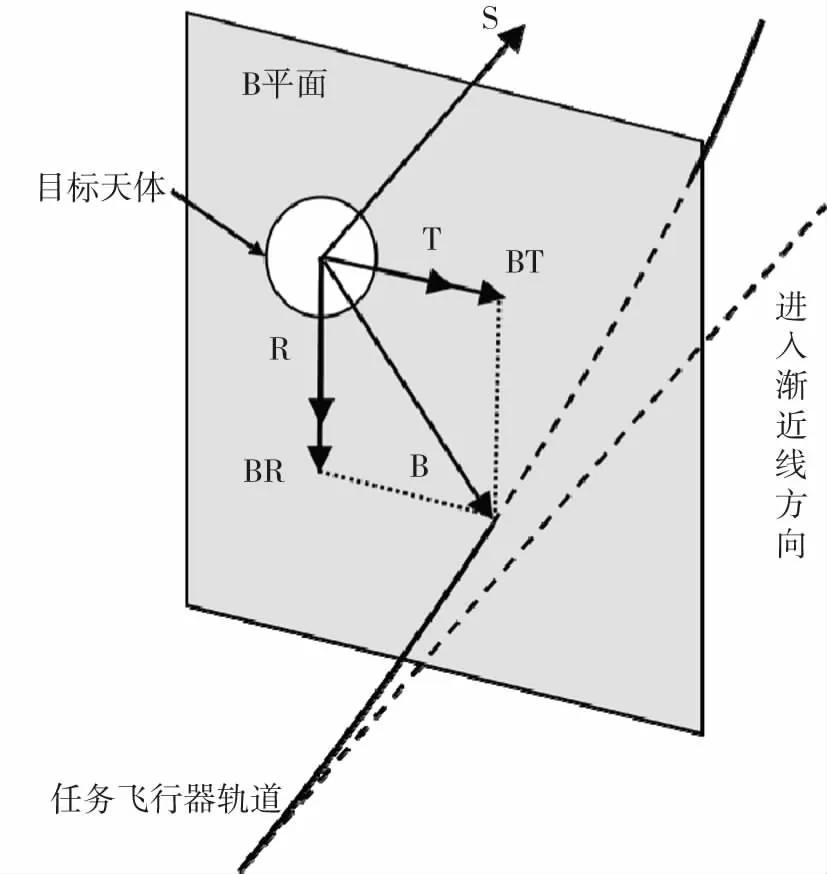
图1 B平面坐标系示意图

(1)

式中：r和v分别表示任务飞行器在惯性系下的位置和速度矢量。则B平面坐标系惯性坐标系的转换矩阵为：

(2)

视线方向与相对位置方向重合，相对位置方向和相对速度方向几乎重合。因此B平面坐标系可以将视线方向的距离独立出来。由于S轴近似表示飞行器进入B平面的方向，T轴和R轴方向的位置信息可以描述任务飞行器与小行星在B平面内的相对位置。故选取B平面坐标系作为相对导航坐标系。

2.1.2 系统状态和观测方程

该任务的中心天体为太阳，同时飞行器与小行星还要受其他大行星引力及太阳光压力等摄动力的影响。飞行器在接近目标天体的末段，其与目标天体所处的位置相差不大，二者所受的太阳引力、摄动力相差很小。在不进行机动时，任务飞行器相对目标小行星近似做匀速直线运动。由于近似所忽略的加速度可视为系统状态噪声。任务飞行器在B平面坐标系下的离散系统状态方程为：

(3)

式中：X=[xyzvxvyvz]T表示任务飞行器在B平面坐标系下的相对位置和速度；t表示滤波步长，Wk-1表示系统状态噪声。

假设光学相对导航相机捷联安装在任务飞行器本体，输出在飞行器本体坐标系下描述的目标视线角，包括俯仰角和方位角。因此观测模型如下：

(4)

式中：qγ和qλ分别表示目标的俯仰角和方位角；Vk表示观测噪声；xb、yb、zb表示r在本体坐标系b系下的投影。xb、yb、zb与系统状态x、y、z的转换关系为：

(5)

2.2 AUKF滤波算法

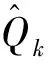
假定非线性系统的状态方程和观测方程具有离散形式，可表示为：

(6)

式中：X表示被估计的随机向量，Z表示对X的观测为随机向量，f和h表示非线性向量函数，Wk和Vk表示不相关的噪声序列，且Wk和Vk满足：

(7)

式中，δkj表示Kronecker算子。

针对线性系统，Sage和Husa提出了基于极大后验估计的噪声统计估值器[11]。将此噪声统计估值器推广到非线性系统，可以得到式(6)对应的非线性时变噪声统计无偏递推估值器为：

(8)

(9)

(10)

(11)

(12)

(13)

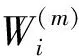
基于无迹卡尔曼滤波算法，结合式(8)～(11)所示的Sage-Husa噪声统计估值器以及协方差匹配思想，可以得到自适应无迹卡尔曼滤波算法。针对式(6)所示的非线性系统，本文提出的自适应无迹卡尔曼滤波算法实现步骤如下：

步骤1，选定滤波初值

(14)

(15)

(16)

(17)

对k=1,2,3…，执行：

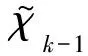
(18)

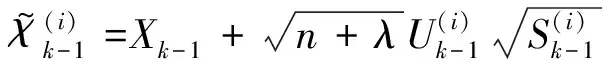
i=1,2,…,n

(19)

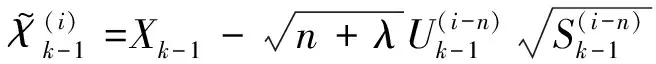
i=n+1,n+2,…,2n

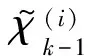
(20)

步骤3，时间更新

(21)

(22)

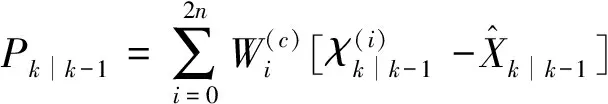
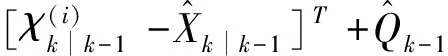
(23)

步骤4，观测更新

(24)

(25)

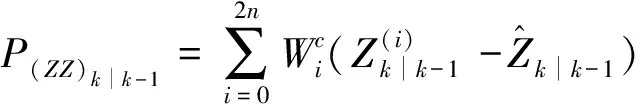
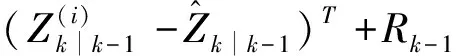
(26)

(27)

步骤5，状态更新

(28)

(29)

(30)

式(28)表示状态增益矩阵更新；式(29)表示状态变量值更新；式(30)表示状态误差方差阵更新。

步骤6，噪声更新

需要特别指出的是，当系统噪声方差阵Q和观测噪声方差阵R均未知时，由于无法从输出中区分系统噪声和观测噪声造成的影响，Sage-Husa噪声估计器无法同时对二者进行估计[12]。因此，需要在一种噪声已知的条件下估计另一种噪声。本文对飞行器相对目标小行星的运动采取了近似处理，忽略的相对加速度为系统噪声，且系统噪声为时变噪声，而观测噪声与敏感器的精度和安装有关，可以预先确定。故本文对系统噪声进行估计：式(8)表示对系统噪声均值的估计；式(10)表示对系统噪声方差的估计。

步骤7，滤波发散抑制

协方差匹配的基本原理是：检验残差与其理论统计特征的相容性，即在滤波过程中，判断残差的统计分布在原假设条件的相容性，当残差在原假设下不相容，则需要根据残差与理论统计特征一致的原则，对协方差阵进行修正。

根据协方差匹配判据，滤波器收敛时应满足：

(31)

式(31)中，εk表示残差序列；γ为事先设定的可调系数，取值范围为γ≥1;tr[·]表示求迹运算。若式(31)不成立，则对Pk∣k-1做如下修正：

(32)

式(32)中，λk的确定规则如下：

(33)

(34)

(35)

式(35)中，μ表示衰减系数，取值范围为0<μ≤1，一般取值为0.95。该系数能进一步提高滤波器的快速跟踪能力。当增大μ时，k时刻之前信息所占的比重减小，当前残差的影响增大。由于沿视线方向的分量是不可观测的，因此在进行修正时，沿视线方向的分量不进行修正。该方法有很强的关于突变状态的跟踪能力，并且在滤波达到稳态时，仍保持对于缓变以及突变状态的跟踪能力。

综上所述，AUKF滤波器计算流程图如图2。

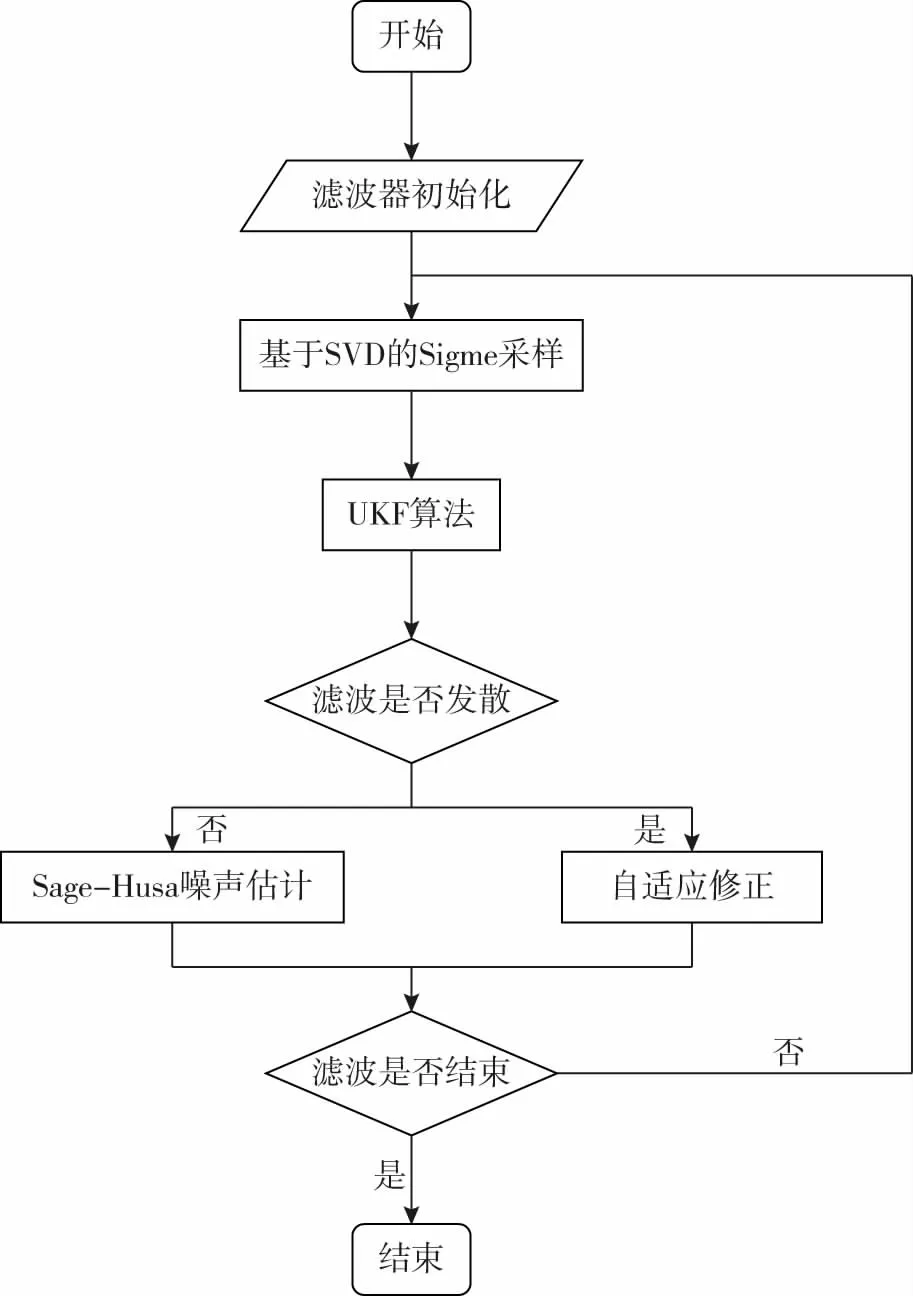
图2 滤波器计算流程图

3 投影脱靶量制导

3.1 投影脱靶量常值模型估计与计算

根据任务飞行器深空自主导航和相对导航结果，能够确定当前时刻任务飞行器与目标小行星在惯性空间的位置与速度，进而可以确定两者的引力加速度GT、GI和飞行器与目标小行星之间的引力差GT/I。针对交会过程的末制导段，交会时刻的引力差很小，即GT/I=0。因此，当前时刻引力差常值模型用式(36)表示：

(36)

式中：ti表示当前时刻，tf表示交会时刻。由式(36)可知，虽然投影脱靶量的计算是一个常数，但是在每次制导计算过程中，通过C0更新来反映当前的引力状态。将式(36)带入的式(37)中且令控制力F=0，并对其进行积分：

(37)

VT/I(t)=C0(ti)(t-ti)+VT/I(ti)

(38)

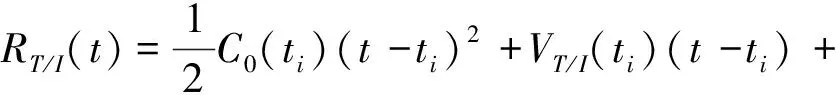
RT/I(ti)

(39)

式中，aT/I、VT/I(t)和RT/I(t)分别表示飞行器与小行星的相对加速度、相对速度和相对位置。

飞行器与小行星的相对距离到达最小值时，应满足的条件是:

VT/I(t)·RT/I(t)=0

(40)

将式(38)和式(39)带入式(40)后得到以交会时间为未知量的方程如下所示：

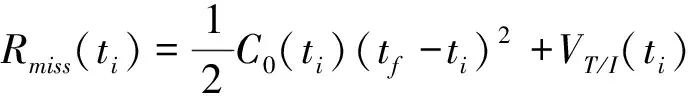
(tf-ti)+RT/I(ti)

(41)

式(41)中，Rmiss(ti)表示ti时刻的投影脱靶量(Projected Miss Distance)。根据式(36)-式(41)，当C0为0的时候常值模型下的投影脱靶量表达式与不考虑相对引力影响的表达式完全一致。另外，式(41)中通过C0引入了用于表达不同引力的高阶项，使得表达式能够更加准确的近似表达引力差的二次项。

3.2 制导律

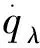
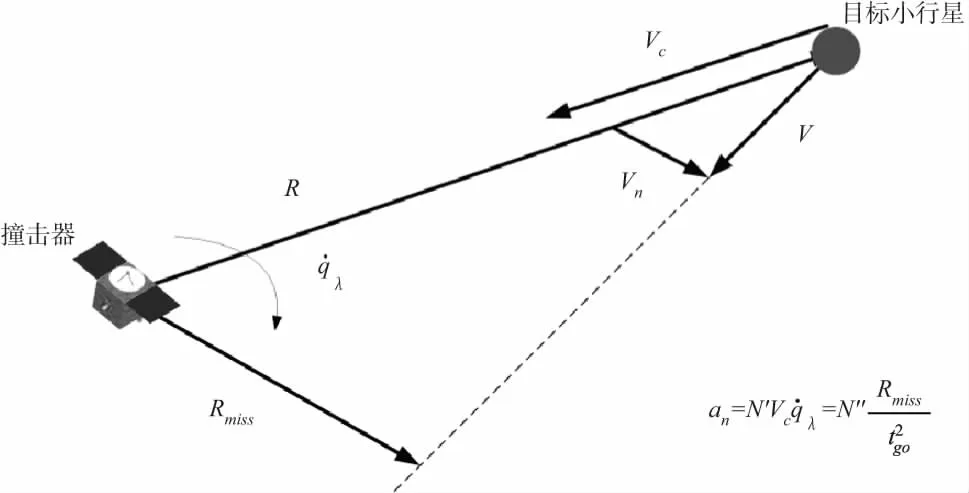
图3 比例导引与投影脱靶量的关系

从图3中可以看出，投影脱靶量还可以表示为：

(42)

(43)

比例导引法是根据飞行器的旋转角速度与目标视线角速度成正比得出的一种导引方法。广义比例导引是针对比例导引的一种改善形式，其一般形式为

(44)

将式(43)带入式(44)，可以得到基于投影脱靶量的制导指令计算形式：

(45)

令tgo=tf-ti，式(45)可以简化表示为：

(46)

上述给出的过载指令均为连续变大小控制量，考虑飞行器无法产生连续可变的制导过载，需要设计高精度的控制输出变换方法，通过脉宽调制等手段生成离散开关控制量，驱动推力器完成实际的推力输出。采用脉冲调宽调频方法(PWPF)，对推力指令进行分配。对于PWPF中的4个参数：放大系数、时间常数、推力器的开关阈值，在实际应用中，通过试凑的方法经仿真试验来确定。

4 仿真实验及分析

4.1 仿真场景

基于潜在威胁小行星Bennu构建小行星防御典型场景，进行仿真验证。Bennu开普勒轨道信息如表1所示[13]。以轨道信息标称值设计飞行任务，任务于2036年9月18日0时开始，交会时间为2037年1月16日0时，交会前4h进入末段导航与制导阶段。小行星实际轨道根据星历误差范围随机选择，小行星直径选择为30m。为验证算法在实际应用中的有效性，除星历误差外引入多种误差源，进行蒙特卡洛仿真分析，误差项及数值如表2所示。

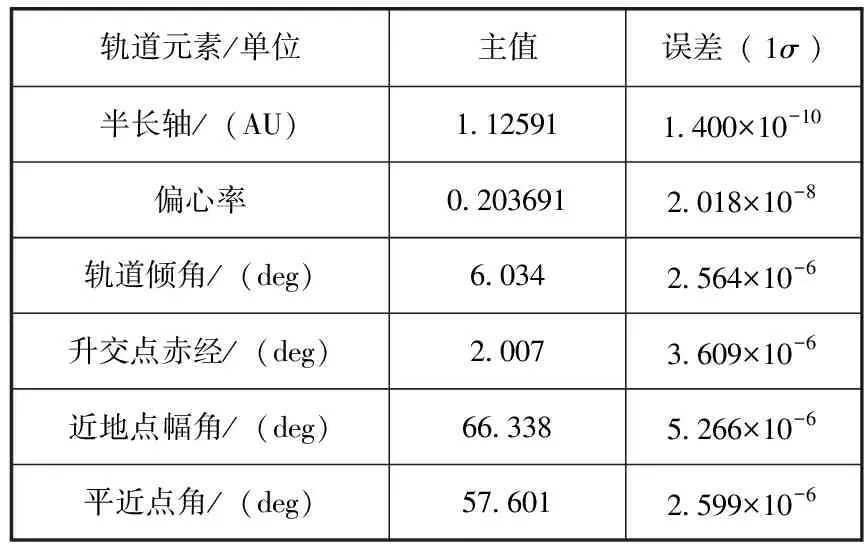
表1 Bennu开普勒轨道信息(时间：59000.0 MJD)

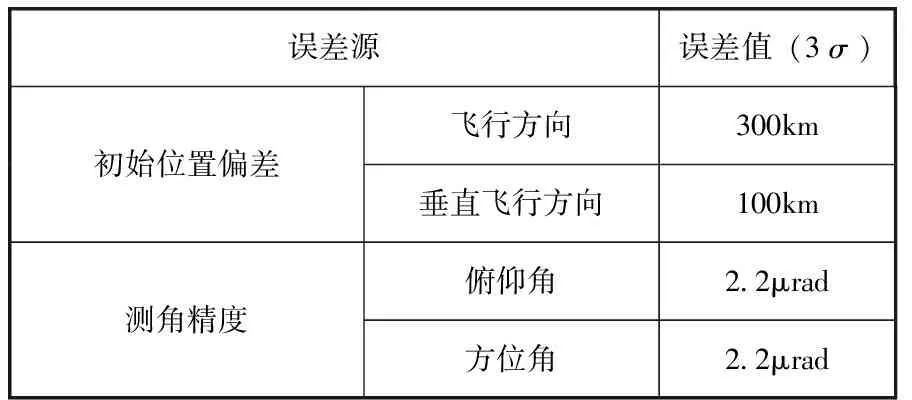
表2 误差源及误差值

4.2 仿真结果与分析

为对比本文提出的算法与其他算法的相对导航效果，在不施加机动的情况下，分别采用EKF算法、UKF算法、不含协方差匹配的AUKF算法以及含协方差匹配的AUKF算法(本文提出的完整算法)进行仿真。目标小行星在J2000日心黄道坐标系的初始位置为[-50119639522.77，130393530773.86，13960229459.83]m，初始速度为[-32208.87，-8047.33，-730.88]m/s，任务飞行器的初始位置为[-50183158838.61，130466720546.96，13974363604.73]m，初始速度为[-27784.43，-13118.19，-1716.38]m/s。在计算滤波器的初值时，目标小行星的初始位置和速度由小行星星历主值计算得出，任务飞行器的初始位置和速度根据真实位置设置测控误差，误差大小如表2所示。本文中采用的滤波初值为[-97946239.90，-241607.05，88444.30，6801.47，0.00，0.00]。滤波器的参数设置一致。系统状态噪声方差阵Q0=diag(1×105,1×105,1×105,1×102,1×102,1×102)，观测噪声方差阵R0=diag(6×10-8,7×10-8)，初始状态误差方差阵P0=diag(1×108,1×106,1×106,1×102,1×102,1×102)，滤波步长为5s，其他参数按上文推荐取值给定。由于飞行器沿视线方向不可观测，在滤波不发散的情况下，该方向的位置和速度的变化趋势与按照初始值递推一致。故仅列出Y轴和Z轴方向的滤波结果，如图4、5所示。

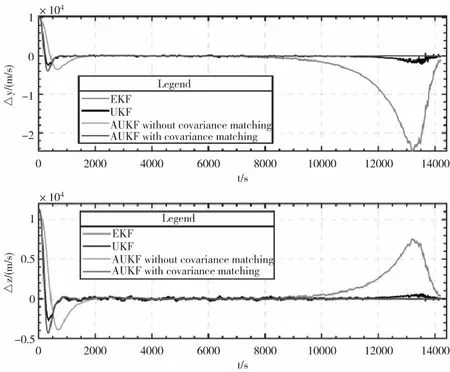
图4 B平面坐标系下位置估计误差

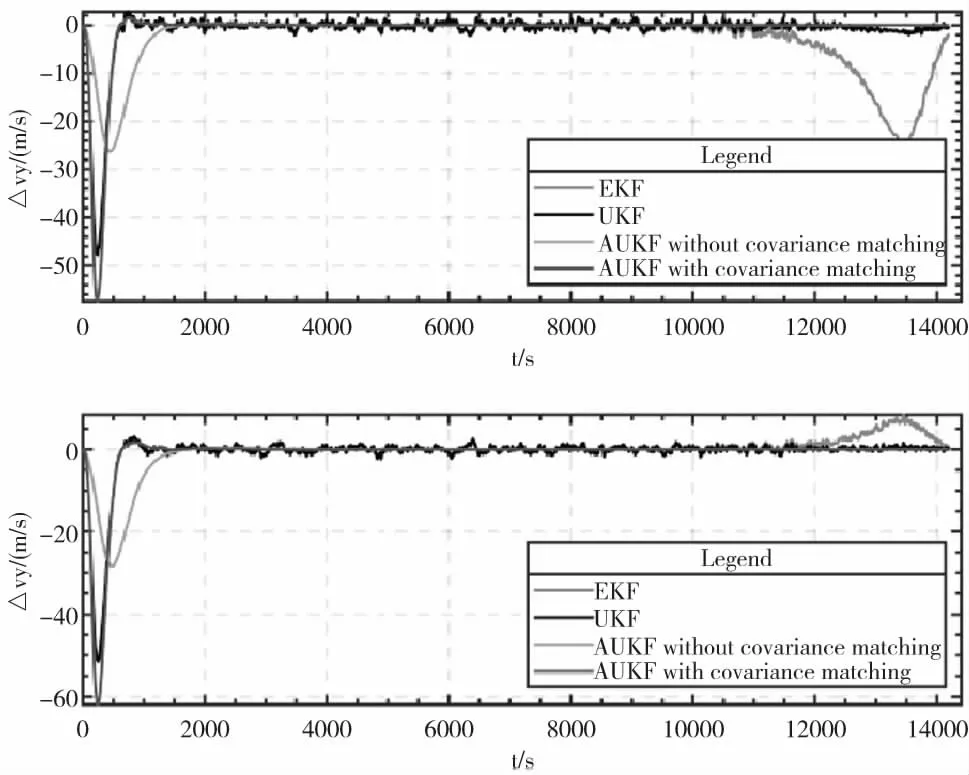
图5 B平面坐标系下速度估计误差

由图4、5可以看出，EKF算法随着滤波时间的增加，累计的误差变大，出现了发散的情况；UKF算法由于预先给出的噪声统计特性存在偏差，估计精度较差；引入噪声估计器后，滤波精度提高，但是收敛速度变慢；利用协方差匹配的思想进行修正，滤波收敛时间从约2000s减小至约1000s。交会前300s，y、z方向的位置滤波误差为6.89m和0.19m，速度滤波误差为0.0016m/s和0.00028m/s。本文提出的相对导航算法具有快速、高精度的特点。

在上述条件下对本文给出的仅测角导航模型相对导航和投影脱靶量制导算法进行仿真验证，飞行器质量800kg，推力大小为5N，交会前两分钟停止控制。制导过程中，B平面坐标系下垂直于视线方向的投影脱靶量的估计值和真实值变化如图6所示。进行200次蒙特卡罗仿真验证，最终交会误差散布图如图7所示。最终交会误差的均方差3σ=5.22m，最大交会误差为6.3m。

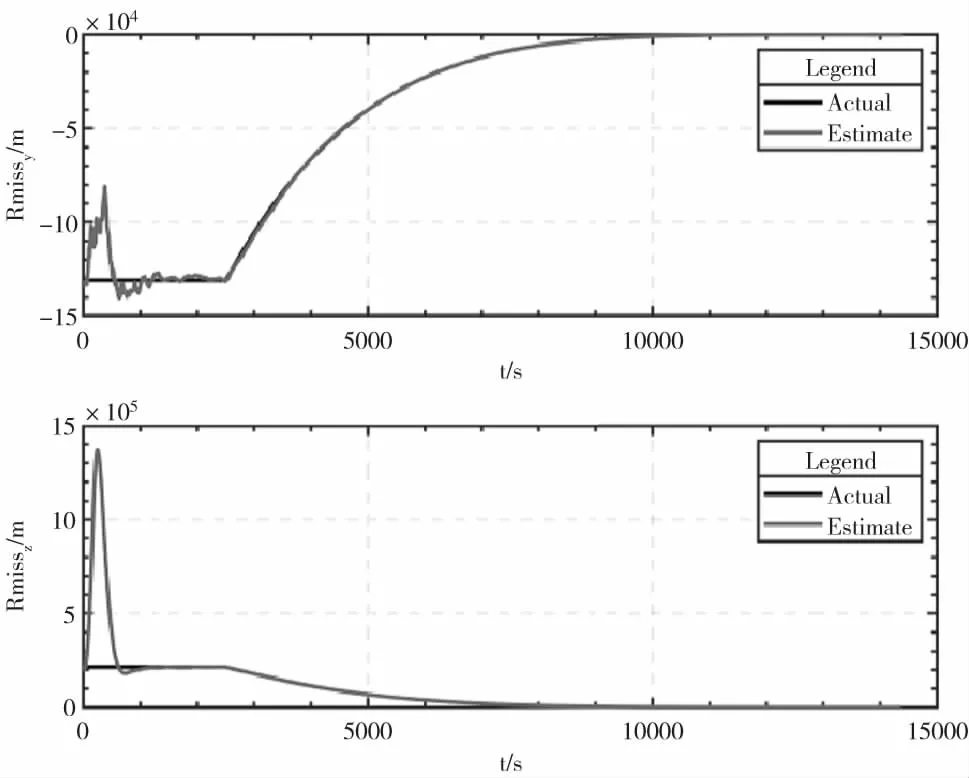
图6 末制导阶段飞行器与导航滤波器表现情况

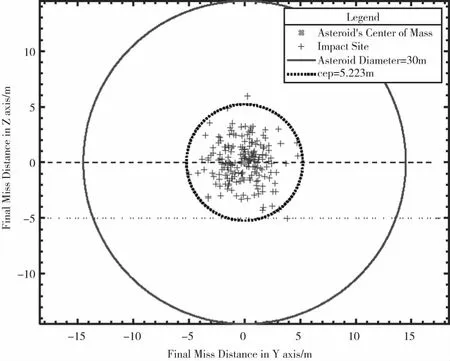
图7 B平面内命中点散布图

5 结论

小行星防御中的目标尺寸更小、目标轨道预报精度更低、交会精度要求更高等问题对相对导航的估计精度和制导精度提出了更高要求。本文首先采用B平面坐标系作为相对导航坐标系，分离出不可观的信息，建立仅测角导航的系统状态方程及观测方程。由于观测方程为非线性方程，本文以UKF算法作为基础滤波算法，避免了线性化后带来的截断误差。考虑系统方程含有未知统计特性的噪声，将Sage-Husa噪声估计器推广到非线性形式，对未知噪声进行在线估计。针对Sage-Husa算法对滤波稳定性及快速性带来的影响，采用协方差匹配思想和奇异值分解方法，加快滤波收敛，提高滤波的稳定性并且保证算法不失效。其次利用相对导航滤波结果，建立了引力差产生的相对加速度的常值模型，计算考虑相对加速度的投影脱靶量，并设计了基于投影脱靶量的制导指令计算方法。最后利用典型小行星防御任务场景进行算法精度验证。由计算机仿真结果表明，本文建立的模型及滤波算法可以对可观测坐标轴方向的状态进行快速准确估计。基于投影脱靶量的制导算法，在复杂引力环境下，能够实现5.22m(3σ)的交会精度。本文的相关研究，能够为我国未来小行星防御任务相对导航与制导系统的设计提供一定的参考和理论依据。