动能撞击偏转小行星的动量传递效率数值仿真研究
2022-02-10陈鸿李毅邹胜宇周浩
陈鸿,李毅,邹胜宇,周浩
(中国空气动力研究与发展中心超高速碰撞研究中心,绵阳 621000)
1 引言
小行星撞击地球可能导致全球范围内的地震、海啸、火山、恶劣气候等灾害,是人类未来面临的潜在危险之一。动能撞击和核爆炸[1]是当前技术条件下使小行星偏离原轨道的两种可行方法,其中,动能撞击方法具有技术成熟和成本低的优点,是应对小尺寸小行星撞击风险的首选手段。衡量动能撞击偏转效率的一个重要指标是动量传递效率,通常采用动量传递因子β表示,其定义为目标小行星获得的动量与撞击体动量之比。动量传递效率与撞击体尺寸、密度、相对速度、目标小行星材料特性和组成结构等诸多因素相关。研究机构和学者开展了大量地面试验研究[2-8],获得了多种材料在超高速撞击条件下的动量传递因子,但地面试验仍然有两项局限性:一是地面试验材料与真实的小行星材料有差异,二是地面试验的尺度有限。为评估动能撞击偏转小行星可行性,NASA和欧洲航天局(ESA)联合开展了AIDA(Asteroid Impact and Deflection Assessment mission)小行星撞击偏转评估任务[9-12],旨在通过真实的撞击,观测评估动能偏转效率,验证地面试验和数值仿真方法。在AIDA任务中,NASA已于2022年9月27日实施了DART(Double Asteroid Redirection Test)试验,这是首个针对近地小行星的撞击偏转试验。DART试验撞击的目标是Didymos(迪迪莫斯)双星系统中的Didymos-B(迪莫弗斯)小行星,观测结果表明该小行星为松散的石质小行星[10, 11],孔隙率和拉伸强度是松散石质材料的主要力学属性,因此,本文采用数值仿真方法研究孔隙率和拉伸强度对动量传递效率的影响。根据地面开展的动量摆试验,利用自主研发的基于欧拉网格的冲击动力学仿真软件NTS[13]开展数值仿真,验证数值仿真方法的可信度,在此基础上基于DART试验计划开展小行星动能撞击偏转过程仿真,分析孔隙率和材料拉伸强度对动能转换效率的影响。
2 数值仿真方法
对小行星的撞击偏转属于超高速碰撞范畴,涉及高温、高压、大变形、材料断裂和破碎问题,一般采用欧拉方法和无网格方法开展数值仿真研究。在小行星撞击问题中,撞击器的尺寸远小于小行星尺寸,网格/粒子尺寸由最小尺寸部件决定,若采用三维数值仿真,则在保证计算精度的前提下,必然导致网格规模过于庞大,对计算资源和时间需求过高。基于以上考虑,本文采用轴对称欧拉方法开展数值仿真。仿真计算中,采用基于自适应欧拉网格的碎片识别算法识别撞击反溅碎片[14],再根据每个反溅碎片的动量计算小行星的动量增量。由于Didymos-B小行星质量较小,在本文计算中不考虑引力作用。
一般情况下,为达到较好的偏转效果,撞击器与小行星相对速度较高,撞击器和小行器材料会发生气化现象,因此需要采用包含相变的状态方程。本文的计算中,撞击器和小行星均采用Tilotson状态方程,参数见表1,参数定义见文献[15]。

表1 AL2024和花岗岩状态方程参数
在本文的仿真中撞击器材料为AL2024,小行星材料采用不同孔隙率的花岗岩代替。金属材料在超高速碰撞下通常会产生软化效应,因此对于撞击器采用Steinberg强度模型。
Steinberg本构模型忽略应变率效应,将材料分为熔化前和熔化后两种状态,在熔化前材料的剪切模量和屈服强度分别如下:
(1)
(2)
式中:G为剪切模量,Y为屈服应力,p为压力,v为体积,T为温度,ε为有效塑性应变,β、n为常数,下标0对应初始值,下标p、T对应参考值。熔化后材料强度直接降为零。
Al2024 Steinberg本构参数见表2。

表2 AL2024 Steinberg本构参数
花岗岩属于脆性材料,而脆性材料本构通常较复杂,需要较多的经验参数,在缺少相关参数的情况下,本文采用弹塑性模型和von Mises屈服准则。碰撞成坑过程中的反溅碎片主要由冲击波在自由面反射形成的拉伸作用和材料的塑性流动形成,因此采用拉伸破坏模型来模拟花岗岩的材料失效。主要参数见表3。

表3 花岗岩本构参数
采用P-α模型[16-18]来模拟花岗岩的孔隙率。在P-α模型中,α为材料膨胀率,其定义为:
(3)
式中:ρS为基体材料密度,ρ为孔隙材料密度。P-α模型的基本假设是,孔隙材料的压力与基体材料压力呈线性关系,内能与基体材料相同,即
(4)
α仅与压力P有关。在本文仿真中采用以下形式的函数。
(5)
式中:Pe为材料处于弹性和塑性分界点时的压力,PS为孔隙完全压实即孔隙率为0时的压力。在本文仿真中Pe为1MPa,PS为213MPa。
3 数值方法验证
为确保数值仿真结果的可信度,对已开展的弹道摆试验[12]进行数值仿真对比验证。弹道摆试验在弹道靶设备中开展,通过发射弹丸超高速撞击采用钢丝悬挂的靶材,根据靶材的摆动测试动量传递因子。采用两种方法测量靶材速度:一是速度法,即根据高速摄影图像分析测量碰撞后靶体质心的平移速度;二是摆角法,即根据弹道摆摆动角度计算靶体在最低点的动能计算靶体平移速度。弹丸为球形铝弹丸,靶材为花岗岩材料,靶材尺寸为110mm×110mm×100mm。撞击参数见表4。采用轴对称模型开展数值仿真,网格尺寸为0.1mm,模拟时长为500μs。

表4 动量摆试验数据及数值仿真结果
在数值仿真中,以撞击点位置垂直速度方向的平面为基准面,计算过程中对通过基准面的反溅碎片的动量进行累加,直至靶材达到稳定状态,再根据反溅碎片动量计算靶材动量。图1是仿真获得的靶材动能变化曲线,靶材在撞击瞬间获得较多动能,此后迅速衰减,到碰撞后300μs之后基本保持不变,可认为300μs之后,靶材速度达到稳定状态,即动量不再变化。仿真计算中采用500μs的模拟时间,可确保此时靶材达到了稳定运动状态。图2是动量摆试验和数值仿真获得的动量传递因子对比。数值仿真获得的动量传递因子与采用速度法测量结果较接近。由于花岗岩断裂的随机性,试验结果具有一定的随机波动范围,而数值仿真中未引入随机因素,因此计算得到的动量传递因子随碰撞速度增加而单调提高[19]。
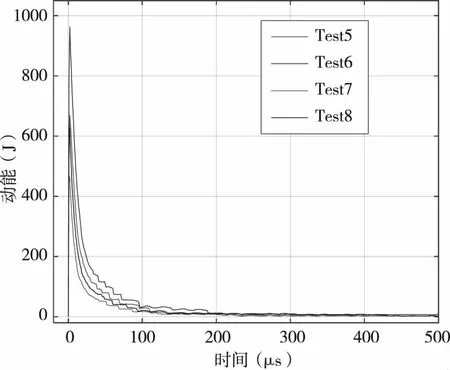
图1 碰撞过程中靶材动能变化曲线(test5)
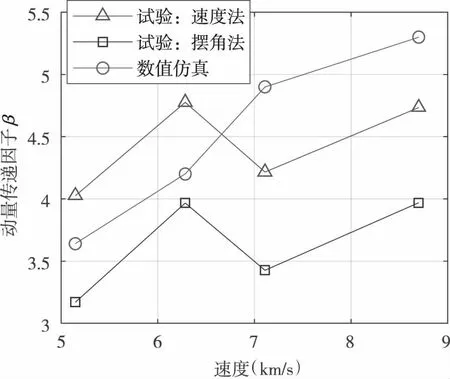
图2 不同工况下动量传递因子对比
4 小行星动能撞击偏转仿真
DART试验撞击的Didymos-B小行星为近似椭球体形状,直径约为160m,为便于计算,将Didymos-B小行星简化为直径160m的均质球形小行星。Didymos-B小行星为碎石堆结构,由岩石块和基体材料组成,目前无法通过观测手段获得其孔隙率和材料拉伸强度。由于基体材料结合力较弱、孔隙率高,参考典型土壤,假定拉伸强度为5kPa,孔隙率为20%;岩石块拉伸强度较高、孔隙率低,参考典型岩石,假定拉伸强度为300kPa,孔隙率为0%~5%。因此,在仿真中拉伸强度范围为5~300kPa,孔隙率范围为0%~20%。
DART试验设计的撞击器质量约600kg,设计撞击速度约6.1~6.6km/s。考虑燃料消耗,在仿真中撞击器简化为直径0.61m、长0.61m的铝合金圆柱体,质量为496kg,撞击速度取6.6km/s。NASA于9月27日实施了DART试验,据报道实际撞击器质量约570kg,撞击速度约6.1kg,本文工作在DART任务实施前完成,计算中采用的撞击器质量和撞击速度与实际情况有一定的差异。
图3是沿撞击方向设置的观测点在撞击过程中的最大冲击压力曲线。在撞击初始阶段,非孔隙材料对应的最大冲击压力高于孔隙材料。在距离撞击点0.2~1m范围内,非孔隙材料和孔隙材料对应的最大冲击压力基本一致。在距离撞击点1m以外,非孔隙材料对应的最大冲击压力随距离衰减速度明显低于孔隙材料。分析其主要原因为:在撞击初期,由于撞击器速度较快,孔隙能够较快从压缩阶段转为压实阶段,因而对应位置的孔隙材料最大冲击压力与非孔隙材料的最大冲击压力基本一致;随着侵彻深度增加,撞击器速度变慢,孔隙从压缩阶段向压实阶段转变速度变慢,从而导致对应位置的孔隙材料最大冲击压力比非孔隙材料有明显的衰减。
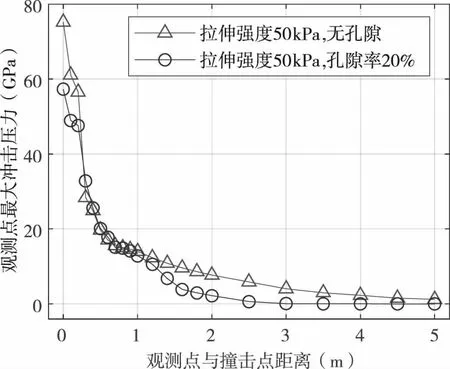
图3 沿撞击方向观测点最大冲击压力曲线
图4是典型仿真工况下的撞击坑形态。在相同孔隙率下,材料拉伸强度越低,则撞击坑尺寸越大,撞击坑的裂纹越长,反溅碎片的破裂程度越高。在相同的拉伸强度下,孔隙材料的成坑尺寸明显小于非孔隙材料对应的成坑尺寸,非孔隙材料撞击坑边缘的断裂程度明显强于有孔隙材料,其主要原因是孔隙材料冲击波衰减速度较快,自由面反射的拉伸波较弱,从而材料断裂程度较轻。
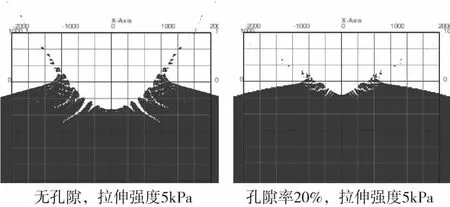
图4 不同工况下撞击坑对比
图5是在典型仿真工况下小行星动能变化曲线。小行星的动能在撞击后较短时间内达到最大值,随着冲击波的传播缓慢耗散直至保持不变,可以认为此时小行星的动量不再变化。当小行星由孔隙材料组成时,在碰撞过程中小行星获得的动能峰值要低于非孔隙材料,动能衰减过程也要迅速得多,能够更快达到稳定状态,这说明孔隙材料在压缩过程中对动能的耗散作用显著,不利于动量传递,这与前述撞击坑形态分析结果相吻合。
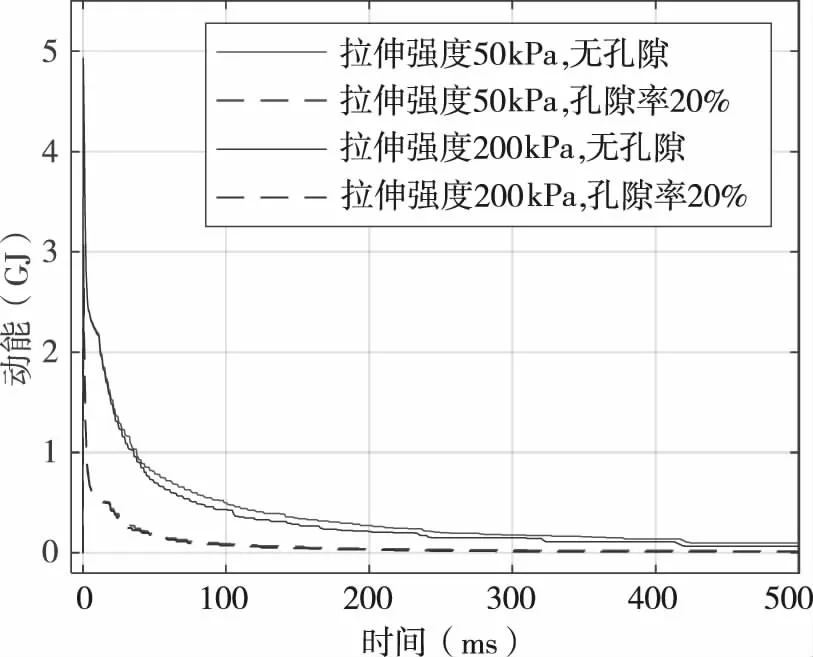
图5 小行星动能变化曲线
图6是典型孔隙率下动量传递因子与材料拉伸强度关系曲线,拉伸强度越高动量传递因子越低。孔隙材料对应的动量传递因子明显低于非孔隙材料。对于非孔隙材料,拉伸强度在200kPa以上时动量传递因子基本保持不变,对于孔隙材料,拉伸强度在100kPa以上时动量传递因子基本保持不变。动量传递因子主要取决于撞击反溅碎片的质量和速度,而材料拉伸强度越低则产生的反溅碎片越多,速度越高,小行星获得的动量越大。对于孔隙材料,在孔隙压缩过程中消耗了较多的动能,导致冲击波强度快速衰减,在边界反射回来的稀疏波较弱,从而导致发生断裂的材料更少,反溅碎片更少,小行星获得的动量越小。
图7是典型材料拉伸强度下动量传递因子与孔隙率关系曲线。当孔隙率范围在0%~10%的范围内时,随孔隙率的增加,动量传递因子迅速下降。当孔隙率大于10%时,随着孔隙率的增加,动量传递因子值基本保持不变。
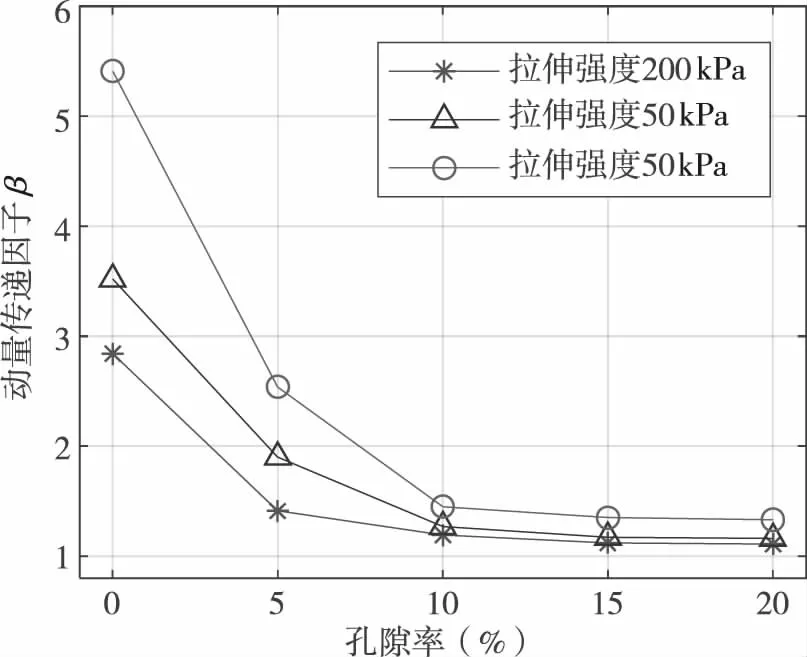
图7 动量传递因子与孔隙率关系曲线
5 结论与展望
基于NASA的DART试验计划,开展了动能撞击偏转小行星数值仿真,分析了材料拉伸强度和孔隙率对动量传递效率的影响规律,结果表明:
(1)采用轴对称欧拉方法开展动量传递效率数值仿真,仿真获得的动量传递因子与试验获得的动量传递因子较为接近,符合动量传递因子随速度变化规律;
(2)在动能撞击小行星偏转仿真中,材料拉伸强度越低,撞击过程产生的反溅碎片越多,撞击坑越大,小行星获得的动量增量越多,动量传递因子越高;
(3)在动能撞击小行星偏转仿真中,材料孔隙率越高,冲击波在传播过程中能量耗散越多,小行星获得的动量增量越少,动量传递因子越低。
小行星撞击动能偏转效率还与撞击点位置、速度、小行星结构形状等因素相关,本文仅考虑了球形小行星,且只考虑了微观孔隙。实际上一些石质小行星大多为非均质松散结构,存在宏观的孔隙和裂纹,因此在下一步工作中将针对宏观松散结构的小行星,开展动能撞击偏转数值仿真,研究动量传递效率的其它影响因素。
