自旋为1的系统的量子非经典性度量
2022-02-10徐为成
徐为成
(西南交通大学物理科学与技术学院, 成都 610031)
1 引 言
在经典物理中并不存在量子态的叠加,这是量子力学独有的特征,也是出现非经典现象的原因之一.量子纠缠就是这类非经典特征的体现.这种非经典特征成为了量子计算和量子信息发展的基础. 为了刻画这种非经典资源,产生了量子纠缠度量,这种度量已经有不少的研究[1,2]. 量子纠缠是描述两个子系统之间的关系,对于单个系统而言,如何刻画单个系统的量子特征成为了研究热点. 2014年, Baumgratz等[3]发表了量子相干度量的文献,这项研究启发了许多量子相干性度量.由不一样的物理背景和不一样的度量工具,产生了许多量子相干性度量的方式. 如l1范数相干性度量[3]、保真度相干性度量[3,4]、迹距离相干性度量[3]、相对熵相干性度量[3]和鲁棒性相干性[5]等.
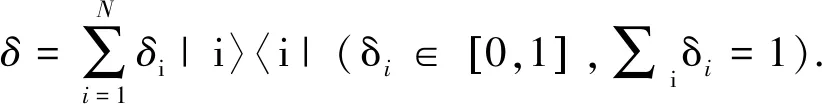

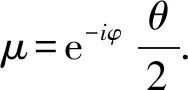
本文基于文献[15]提出自旋为1的态的非经典性度量, 给出一些性质和计算例子. 利用一个与态ρ有关系的矩阵Z是否为半正定的引出一个非经典性度量.Z的元素:
Zab=Wab-uaub
Wab=trρ(JaJb+JbJa)-δab
ua=tr(ρJa)
(1)
本文第二部分介绍经典的态的定义和特征,第三部分提出一个非经典性度量,第四部分为计算例子.
2 经典的态的定义和特征

(2)
一个自旋为1的密度矩阵ρ可以表示成:
(3)
其中Ja是j=1的角动量算子,ua=tr(ρJa),Wab=trρ(JaJb+JbJa)-δab,u∈R3,W是一个3×3的实对称张量. 通过文献[10] ,当且仅当3×3的实对称矩阵Z是半正定的,密度矩阵ρ是经典的,矩阵Z的元素Zab=Wab-uaub.
3 非经典性度量

现在提出一个度量, 即:
(4)
经过计算,

(5)


证明:
(6)
证毕.
性质c:纯态的非经典性N(|Ψ><Ψ|)≥N(|n> 通过简单运算知N(|1,1><1,1|)=0,由性质b得 N(|n> N(|1,1><1,1|)=0 (7) 证毕. ny,nz). (8) (9) 所以对于Dicke态ρ=|1,0><1,0|是非经典的. (10) |j+m>⊗|j-m>,(m=-j,…,j) |j,-j>=|0>⊗|2j> (11) 考虑最大纠缠态 (12) 意味着完全混合态对应的矩阵Z是半正定的,所以完全混合态是经典的,这也与文献[15]一致. P(1-min(2nx2+2nz2))- 选 (13)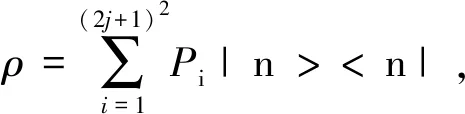
4 计算例子

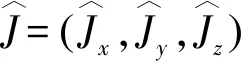



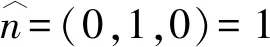
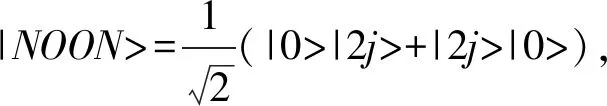
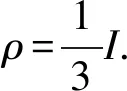
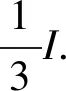


5 结 论

