基于最有价值球员算法的结构损伤识别方法 *

2022-02-10缪炳荣彭齐明杨树旺雒耀祥裘杨喆

重庆交通大学学报(自然科学版) 2022年1期

缪炳荣，彭齐明，杨树旺，雒耀祥，裘杨喆

(西南交通大学牵引动力国家重点实验室，四川成都 610031)

0 引言

由于材料疲劳、老化、过度变形以及超载和恶劣的环境条件等原因，轨道车辆结构不可避免地会累积损伤，最终严重危害轨道车辆安全运行和寿命，造成人员和基础设施重大损失。因此，对结构损伤进行早期检测，及时对结构损伤部位进行维修，以确保结构安全。

结构系统中的损伤会引起模态参数变化，如固有频率、振型、振型曲率、模态应变能、频响函数等，这些参数可作为判断损伤状态的信号，其中固有频率和振型在损伤识别中应用最广。李旭娟等[1]利用振型和离散小波变换对不同边界条件下的板进行损伤识别研究，用对角细节分量小波系数成功定位和量化损伤；殷红等[2]利用频响函数进行损伤识别，并对传感器布置优化进行了研究；夏志鹏等[3]利用交叉模态应变能和Tikhonov正则化识别一海洋平台结构损伤；蒋舸等[4]利用结构残余力和最小秩修正法来识别3D桁架结构损伤。考虑到结构损伤识别可看作是一个优化问题，近年来智能优化技术在结构损伤识别研究中得到了关注，如遗传算法(GA)、粒子群算法(PSO)、差分进化算法(DE)、蚁狮优化算法(ALO)等智能优化算法。张晓东[5]利用遗传算法和仅含固有频率的目标函数准确识别了损伤程度较大的简支梁单处损伤。N.B.GUEDRIA[6]提出了一种改进的DE算法，并对板和层合板进行损伤识别分析；D.C.DU等[7]提出了一种多阶段优化识别方法，提高了收敛速度和识别精度；D.C.DU等[8]利用Jaya算法研究了不同目标函数下结构损伤识别效果；M.MISHRA等[9]利用ALO算法识别结构损伤，并与改进的PSO算法识别效果进行对比，结果表明ALO算法识别结果更加可靠；CHEN Zepeng等[10]采用PSO和Nelder-Mead相结合方法，大大提高了结构损伤识别精度；V.D.TRUNG等[11]提出了一种基于模态应变能和改进DE算法的两阶段结构损伤识别方法；H.R.E.H.BOUCHEKARA[12]提出了一种新的智能优化算法，即最有价值球员算法(MVPA)，MVPA显著特点是需要确定的参数少，收敛速度更快、精度更高；J.MILAD等[13]采用MVPA及其他优化算法进行结构损伤识别，研究结果表明MVPA识别效果明显优于其他优化算法。虽然这些方法都取得了比较满意的识别效果，但它们均未考虑不确定性因素对识别结果的影响。不确定性因素包括计算模型参数的不确定性和模型误差；前者是结构进行数学建模所造成的，其参数可能会受到一定程度的统计变化；后者为建模过程可能会引入的建模误差[14]。

笔者基于MVPA，利用结构振型和固有频率构建目标函数来进行结构损伤识别。结构损伤在物理空间上具有稀疏性，即结构少量单元或子结构出现损伤，通过在目标函数中引入罚函数以加强求解结果精度。以一简支梁和桁架结构为例，考虑不确定性因素和噪声影响，对比不同目标函数下的损伤识别效果。研究结果表明：即使在不确定性因素和高噪声水平影响下，笔者的方法也具有准确可靠的识别效果。

1 最有价值球员算法(MVPA)

MVPA是一种求解优化问题的新型基于元启发式群体算法，其灵感来自于国际篮球锦标赛，具有简单易实现、控制参数较传统算法少、鲁棒性强、运行高效等优点。其核心思想是通过模拟运动员间以团队和个人形式的竞争来获得优化问题的最优解。通过团队成员随机组成和运动员竞争后个人技能的更新实现全局搜索，贪婪策略和精英策略的引入提高了团队多样性和算法寻优性能，加快算法收敛速度，避免陷入局部最优。MVPA流程如图1。

图1 MVPA流程Fig. 1 Flow chart of MVPA

1.1 团队形成

对于D维优化问题，假设共有N位运动员，每位运动员拥有D项技能，即每位运动员对应着优化问题的一个解。

xi={xi1,xi2,…,xiD}表示第i位运动员，其中：xij∈[lj,uj]为第i位运动员的第j项技能，uj和lj分别对应第j项技能的上限值和下限值。一旦运动员的数量确定，将以随机组队方式形成nT个团队，如式(1)：

(1)

式中：nP1、nP2分别为团队1、2中的运动员人数；nT1、nT2分别为团队中人数为nP1、nP2的团队数；N为团队总数；Ceil为一个将实数四舍五入为最小整数的函数，故可能出现nP1≠nP2，这大大增强该算法的灵活性。

1.2 技能提升

团队形成后，每个运动员将会提升自己技能。团队i中运动员Ti技能更新计算如式(2)：

Ti=Ti+Rand(Fri-Ti)+2Rand(TMVP-Ti)

(2)

式中：Rand为[0, 1]均匀分布随机数；Fri为团队i中的特许运动员，即团队i中最好或最有价值的运动员；TMVP为所有运动员中表现最优异的运动员。

1.3 团队竞争

团队组建且技能更新完成后，假设随机选取两个团队Tx和Ty进行团队间比赛，并规定团队间的比赛没有平局。为确定获胜球队，需对给定团队Ti的适应度进行归一化处理，如式(3)：

Fnorm,i=Fi-min(F1,F2,…,FnT),

i=1,2,…,nT

(3)

式中：Fi和Fnorm, i分别为团队i归一化前后的适应度值。

团队Tx打败Ty的概率如式(4)：

(4)

由于不确定性因素，即使Tx比Ty有更高的获胜概率，Ty仍有获胜可能。故为了确定最终获胜的团队，将产生一个随机数来决定最终获胜者。若该随机数大于两队中获胜较大的概率，则获胜概率低的团队获胜。

两队比赛结束后各队运动员技能如式(5)。当团队Tx获胜时取“+”，团队Ty获胜时取“-”。

Tx=Tx±Rand×(Tx-Fry)

(5)

式中：Fry为团队Ty中的特许运动员。

1.4 边界限制

由于技能存在边界限制，需对运动员xi技能作出如式(6)约束：

(6)

1.5 贪婪策略

(7)

1.6 精英主义

在此阶段，第k+1次迭代更新后的所有运动员中表现较差的一部分将由第k次迭代后表现最好的一部分运动员替代，如式(8)：

(8)

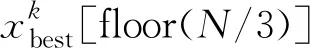
2 结构损伤识别

2.1 局部损伤参数化

对于一个n自由度无阻尼结构，其特征方程表征如式(9)：

(K-λiM)φi=0

(9)

式中：K、M分别为结构整体刚度矩阵和整体质量矩阵；λi、φi分别为结构第i阶特征值及相应振型。

结构损伤将通过每个单元的刚度折减变量dj(j=1, 2,…,Nele) 来模拟结构局部损伤发生；且由于结构损伤对其质量的影响可忽略，结构损伤情形可由式(10)表示：

(10)

式中：Kd为结构有损伤下的整体刚度矩阵；Kj为第j个单元在整体坐标下的单元刚度矩阵；dj为第j个单元的损伤因子，且dj∈(0,0.99)，其中dj=0表示第j个单元没有发生损伤，dj=0.99表示第j个单元已经完全损坏；Nele表示结构单元总数。

2.2 目标函数

从数学角度而言，损伤识别问题可看作是一个非线性优化问题。优化问题中目标函数一般定义为实际测量结构振动响应与有限元模型分析响应之间的误差，通过最小化该误差可定位和量化结构局部损伤。故目标函数选择对损伤检测过程成功与否有着广泛影响。

传统目标函数是根据固有频率和模态保证准则(MAC)变化来定义的，记为obj1，如式(11)～式(13)：

(11)

(12)

(13)

在obj1基础上引入罚函数，记为obj2，如式(14)～式(15)：

(14)

(15)

式中：L(d)为罚函数；M(d)为优化识别时，当前迭代步识别结果向量中数值大于零的个数。

根据结构固有频率和振型建立新的目标函数，记为obj3，定义如式(16)：

(16)

(17)

式中：E为期望值运算符。

在目标函数obj3基础上同样引入罚函数L(d)，记为obj4，定义如式(18)：

(18)

2.3 不确定性因素和噪声影响

为更加真实的贴近工程实际，考虑不确定性因素和噪声影响。在单元刚度参数中引入1%的变化量来模拟不确定性因素影响。为模拟噪声影响，按式(19)对固有频率和振型施加随机噪声：

γ*=γ(1+LnRn)

(19)

式中：γ*和γ分别为含噪声和不含噪声的模态参量；Ln为噪声等级；Rn为随机矩阵，矩阵内每个数均为[-1, 1]的随机数。

2.4 损伤识别结果误差表示

考虑到微小损伤设定损伤值较小，即使识别结果与设定真实损伤值存在微小差异都会使得损伤指标百分比误差(δerror)很大，因此规定其计算如式(20)：

(20)

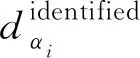
3 数值算例

采用MVPA最小化提出的目标函数求解得出结构损伤位置和程度，并对比4种不同目标函数下的损伤识别效果，另外考虑1%不确定因素和噪声影响。

以一简支梁和桁架模型为数值仿真对象，取结构固有频率和垂直方向上振型数据用于结构状态识别[15]。笔者分别对1～6阶模态数据代入验证，发现这6阶识别效果最佳，限于篇幅并未考虑模态阶数对识别结果影响。考虑到针对某一损伤工况，MVPA独立运行次数与计算结果精度和计算时间有关，即运行次数越大，计算结果精度越高，但计算时间越长。综合考虑，对每一损伤工况独立运行10次，取其平均值作为最终识别结果，通过标准差衡量MVPA在不同目标函数下的稳定性；标准差越小，其稳定性更强，得到的结果更加可靠。

3.1 简支梁模型

简支梁有限元模型如图2。模型参数为：弹性模量Eb=206 GPa；横截面面积Ab=3×10-4m2；惯性矩Ib=6.25×10-10m4；密度ρb=7 800 kg/m3。梁全长0.75 m，共划分为15个单元。图2中：①、②、…为单元编号，1、2、…、16为节点编号。MVPA参数设置为：运动员总数N=70，团队总数nT=7，最大迭代次数Gmax=500。简支梁损伤工况设置如表1。

图2 简支梁有限元模型(单位：mm)Fig. 2 Finite element model of simply supported beam

损伤工况损伤单元@程度C13@0.05C23@0.10C33@0.20、11@0.20

在obj1～obj4这4种目标函数下，分别独立运行10次，并取其平均值作为最终识别结果。值得注意的是，为确保识别效果具有可比性，每次独立运行时，各目标函数中添加噪声后的振型和固有频率数据完全一致，其中：对固有频率添加1%、振型添加5%的随机噪声。笔者以损伤工况C1和C3为例进行描述。

单处微小损伤工况C1识别结果如图3。

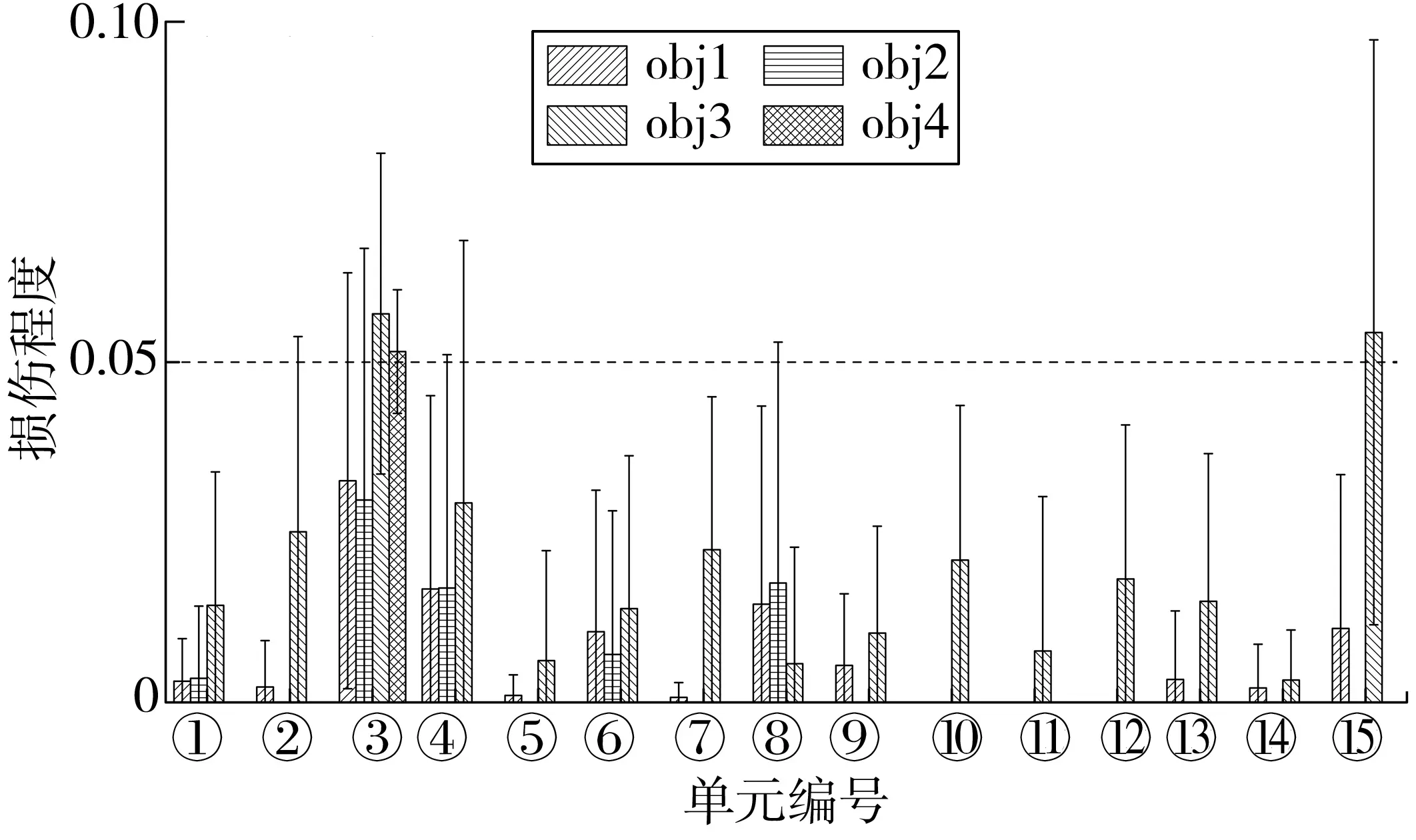
图3 简支梁损伤工况C1识别结果Fig. 3 Identification results of damage case C1 ofthe simply supported beam

假设单元③的刚度折损量为5%，即d3=0.05。从图3中可知：obj1～obj4均能准确定位和量化损伤；相比之下，obj1和obj2在损伤单元③处的损伤量化误差比obj3和obj4大；此外，obj1～obj3均引入了大量损伤误判单元，其中obj3尤为明显，特别是在边界单元号处出现严重误判；从识别稳定性而言，对微小损伤情形，各目标函数识别结果不太稳定。

损伤单元指标d3变化曲线和各目标函数适应度值收敛曲线分别如图4、图5。

从图5中看出：各目标函数的适应度值曲线分别在10、100、300和150次收敛；对应图4中各目标函数的d3变化曲线的收敛趋势，其中：obj1和obj2由于过早收敛，导致其识别效果不理想；而obj3和obj4在经过更多次迭代后更加接近真实损伤值。

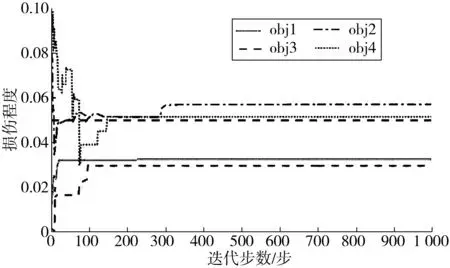
图4 不同目标函数下识别损伤指标d3收敛曲线Fig. 4 Convergence curve of damage index d3 underdifferent objection functions

图5 简支梁损伤工况C1适应度值变化曲线Fig. 5 The fitness value variation curve of simply supported beamunder damage case C1

多处损伤工况C3识别结果如图6。假设③、单元刚度折损量均为20%，即d3=d11=0.2。

图6中：obj1～obj4均能定位和量化损伤，量化误差程度上，obj1最大；obj1～obj3均引入大量误判损伤单元信息，但误判损伤程度均很微小，仍可看作无损单元。

图6 简支梁损伤工况C3识别结果Fig. 6 Identification results of damage case C3 ofthe simply supported beam

损伤单元指标d3、d11和各目标函数适应度值收敛曲线分别如图7～图9。从图8中看出：各目标函数适应度值曲线分别在80、120、550和800次左右收敛。obj1和obj2同样存在着过早收敛的问题，导致其识别精度不高；obj3和obj4虽收敛较晚，但是其收敛值更加接近真实损伤对应的适应度值。

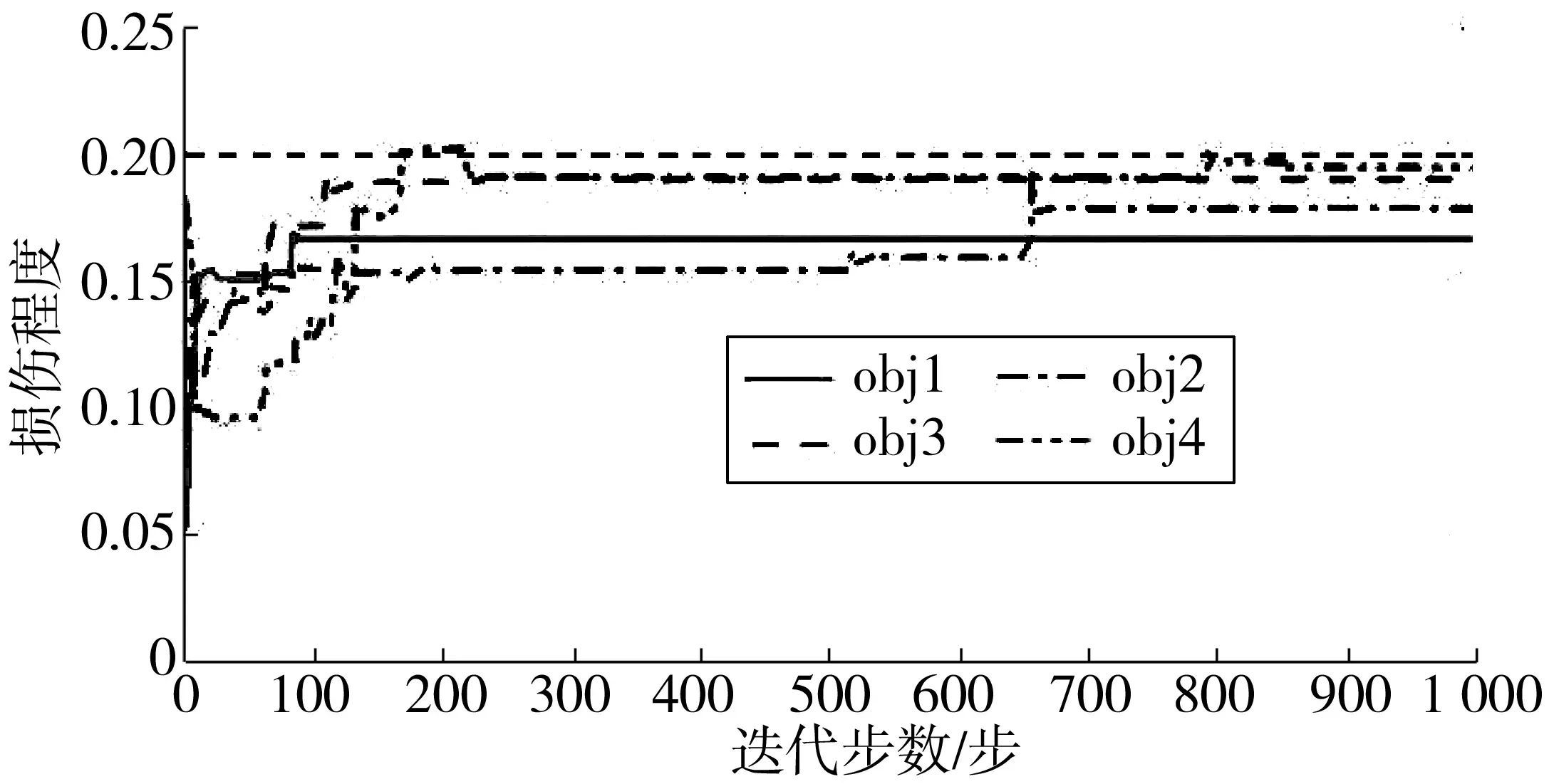
图7 不同目标函数下识别损伤指标d3收敛曲线Fig. 7 Convergence curve of damage index d3 underdifferent objection functions

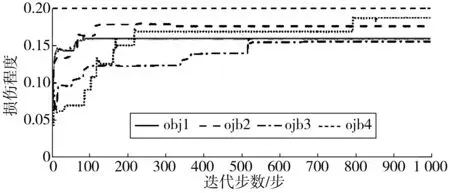
图8 不同目标函数下识别损伤指标d11收敛曲线Fig. 8 Convergence curve of damage index d11 underdifferent objection functions

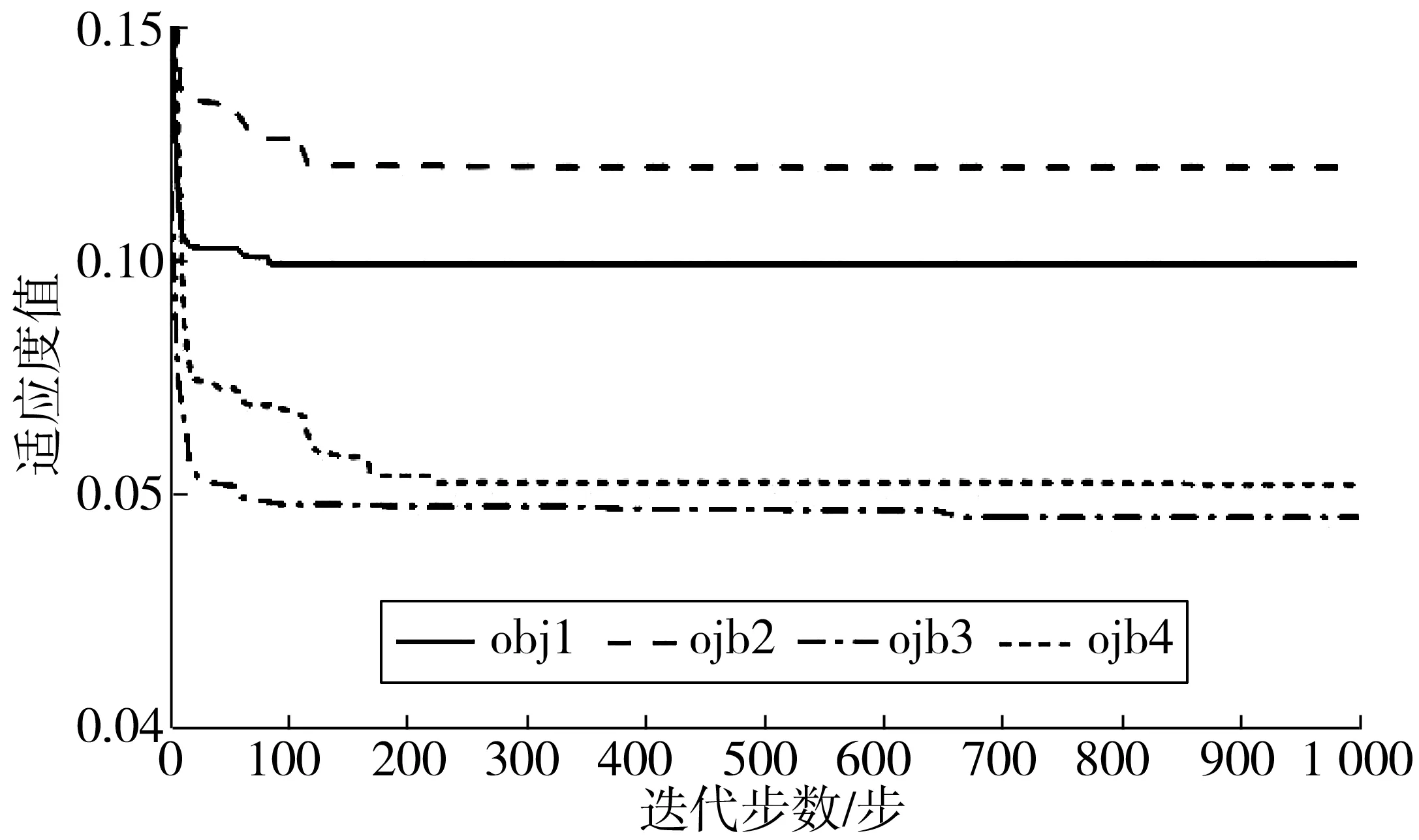
图9 简支梁损伤工况C3适应度值变化曲线Fig. 9 The fitness value variation curve of simply supported beamunder damage case C3

简支梁损伤工况C1～C3下各目标函数识别结果如表2。由表2可见：在5%噪声水平下，obj1和obj3识别损伤误差均小于6%；从各损伤工况识别误差和标准差来看，obj3识别效果要优于obj1。而分别在obj1和obj3基础上引入罚函数后的obj2和obj4误差分别小于3%、2%，可见罚函数的引入对识别精度有较大提升。obj4在4个目标函数中识别效果最佳，不仅定位和量化损伤能力最强，而且识别稳定性也最高，即识别效果最可靠。

3.2 桁架模型

桁架有限元模型如图10。模型参数：密度ρt=7 850 kg/m3；弹性模量Et=200 GPa；横截面面积At=7.85×10-3m2。桁架共划分为26个单元。图10中：①、②、…为单元编号，1、2、…为节点编号。MVPA参数为：运动员总数N=70，团队总数nT=7，最大迭代次数Gmax=300。取前6阶固有频率和垂直方向上振型用于结构状态识别。桁架损伤工况设置如表3，分别考虑了横杆、立杆和斜杆处损伤对识别效果影响。

表2 简支梁损伤识别结果Table 2 Damage identification results of simply supported beam

图10 桁架有限元模型(单位：mm)Fig. 10 Finite element model of truss

表3 桁架损伤工况Table 3 Damage cases of truss

在obj1～obj4这4种目标函数下，分别独立运行10次取其平均值作为最终识别结果，其中：对固有频率添加1%、振型添加3%的随机噪声。以损伤工况C1和C3为例进行描述。

单处损伤工况C1识别结果如图11～图13。假设单元②刚度折损量为5%，即d2=0.05。从图11可知：obj1～obj4识别效果很差，无法准确定位和量化损伤，在非损伤单元处识别出大量严重的虚假损伤；obj1～obj3虽在单元②处的损伤识别值接近真实值，但是其稳定性太差，表现为其每次识别的损伤值变化太大。

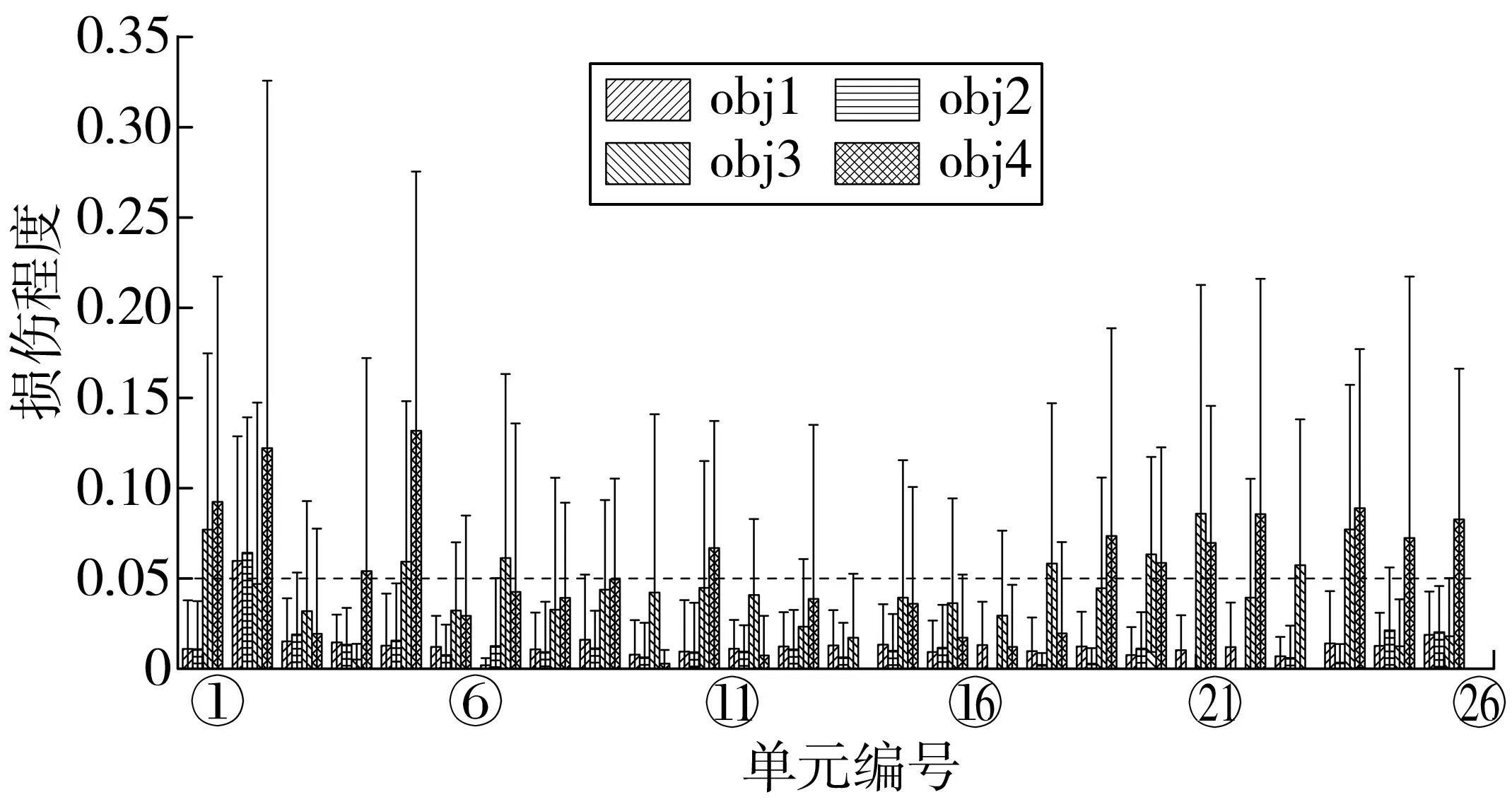
图11 桁架损伤工况C1识别结果Fig. 11 Identification results of truss under damage case C1

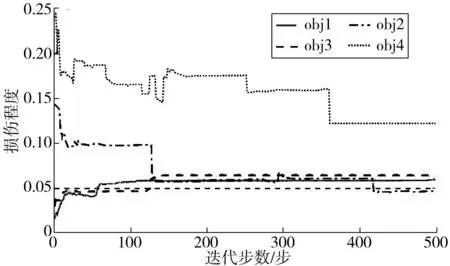
图12 不同目标函数下识别损伤指标d2收敛曲线Fig. 12 Convergence curve of damage index d2 underdifferent objection functions

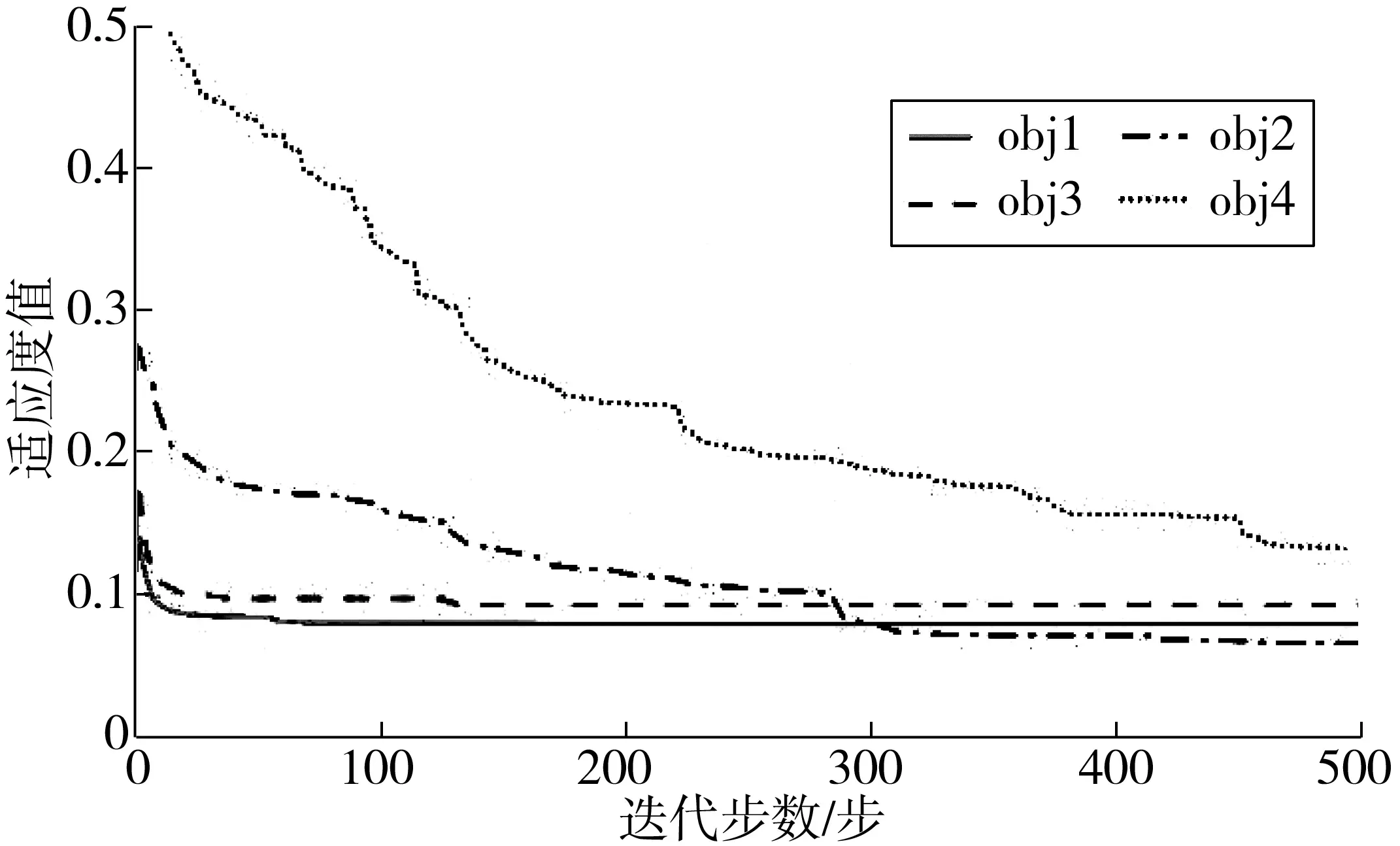
图13 桁架损伤工况C1适应度值变化曲线Fig. 13 The fitness value variation curve of truss under damagecase C1

多处损伤工况C3识别结果如图14～图16。从图14、图15可看出：obj1、obj2适应度值曲线过早收敛；obj3先振荡后收敛；obj4一直处于振荡过程，其损伤单元处识别损伤指标值一直处于振荡状态。总体来看，在微小损伤工况下，obj1～obj4无法达到理想的损伤识别效果。假设单元②、的刚度折损量分别为20%、30%，即d2=0.2，d18=0.3，各单元识别结果如图14。obj1～obj4均能定位和量化损伤，其中：obj3、obj4识别效果较好；虽然obj1～obj3均引入大量微小误判损伤单元信息，但可看作无损单元，对识别效果影响不大。损伤单元指标d2、d18和各目标函数适应度值收敛曲线分别如图15、图16。虽然obj2在obj1基础上引入了罚函数来增加识别结果稀疏性，但从两者适应度值变化曲线(图16)上来看，obj2没有出现过早收敛问题；从损伤单元指标变化曲线(图15)看，罚函数的引入并没有使其识别损伤值更加接近真实损伤值；而在obj3基础上引入罚函数的obj4来说，obj4的识别效果更好，不仅在真实损伤单元处量化误差更小，而且虚假损伤误判信息大大减少。

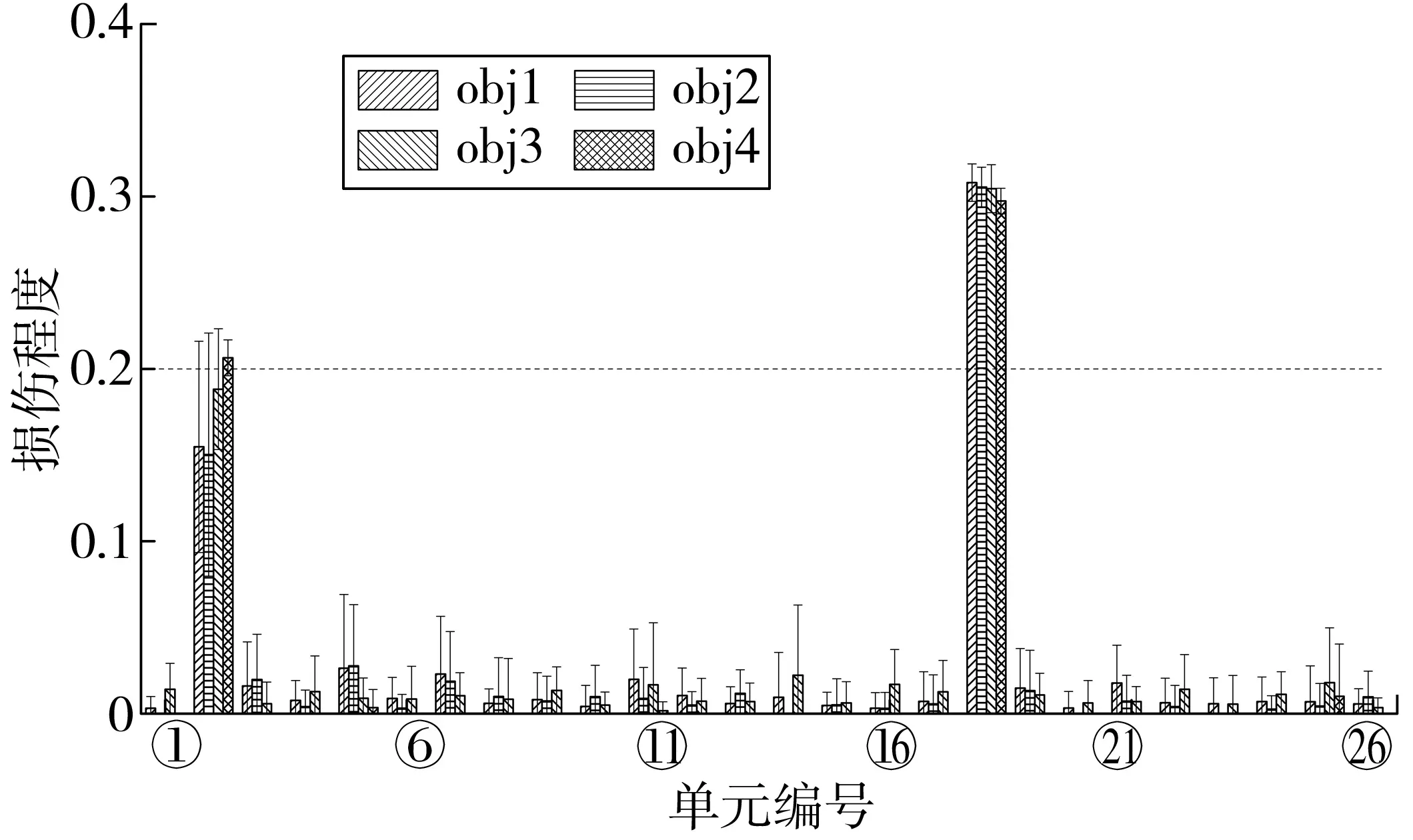
图14 桁架损伤工况C3识别结果Fig. 14 Identification results under of truss damage case C3

图15 不同目标函数下识别损伤指标d2和d18收敛曲线Fig. 15 Convergence curve of damage index d2 and d18 underdifferent objection functions

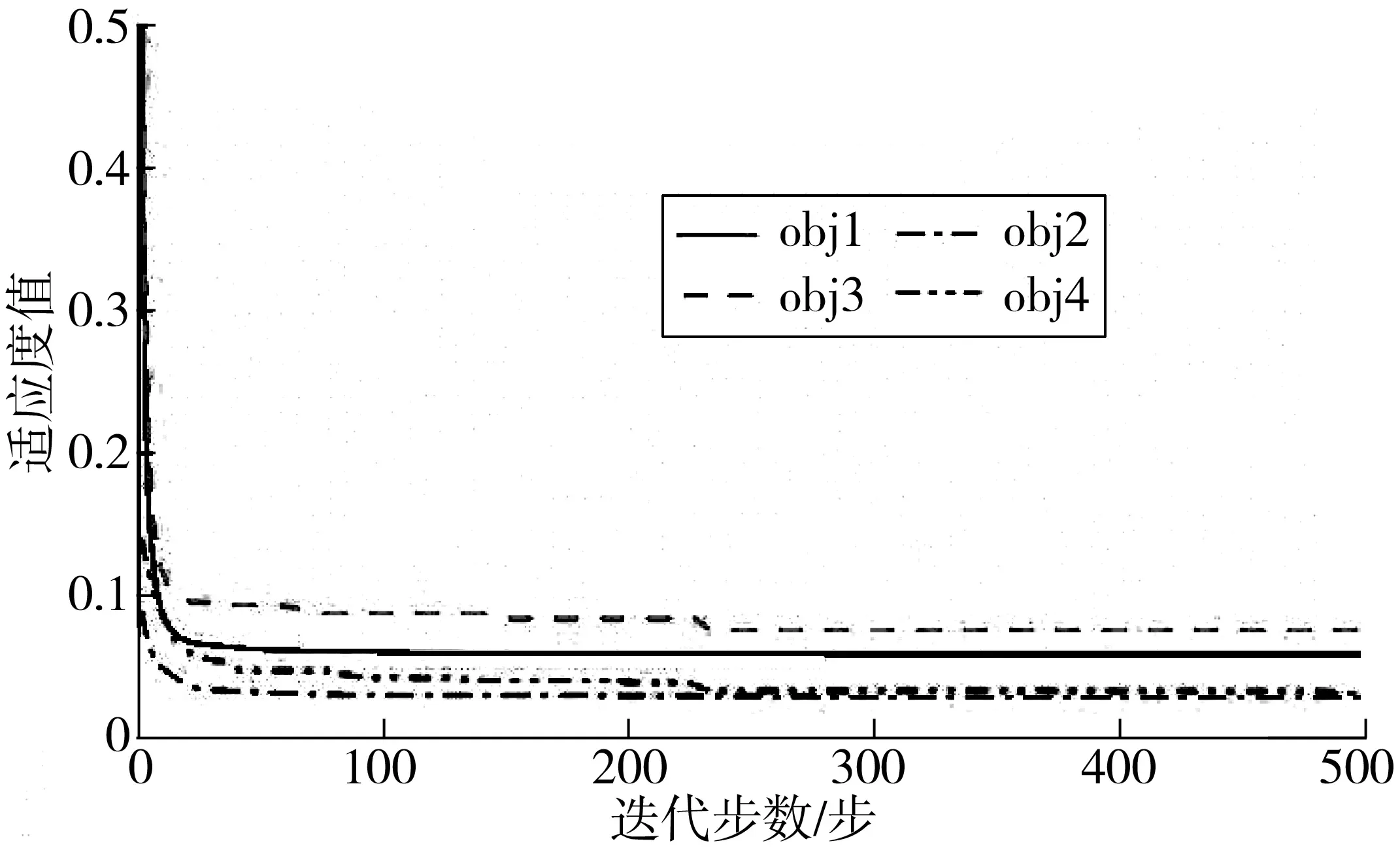
图16 桁架损伤工况C3适应度值变化曲线Fig. 16 The fitness value variation curve of truss under damagecase C3

桁架损伤工况C1～C4下各目标函数识别结果如表4。由表4可知：在3%噪声水平下，除了损伤工况C1，其他损伤工况识别效果均比较好，obj1～obj4最大识别误差分别为7.26%、9.18%、6.11%和7.81%，且均出现在C4中损伤程度设置较小单元处。对比obj1～obj4识别结果发现，罚函数的引入对obj1提升识别精度效果不明显，甚至有时起到反作用，例如工况C4；而罚函数的引入对obj3识别结果有较大改善效果，具体体现在C2～C4识别效果的改善。

表4 桁架损伤识别结果Table 4 Damage identification results of truss

3.3 结果分析

在简支梁模型和桁架模型中，MVPA在obj4下识别效果都是最好的，其次为obj3。对于微小损伤情形，在简支梁模型中的4种目标函数下识别结果均较好，但在桁架模型中却均失效，连损伤位置都无法准确定位。在obj1、obj2下的计算结果易陷入局部最优，出现过早收敛现象，导致其在某些工况识别效果不太理想。在这两种模型中，obj1～obj3识别效果中均出现损伤误判现象。比较明显的是：在桁架模型中，obj1、obj2对横杆单元损伤并不是特别敏感，导致其对横杆识别误差比立杆和斜杆要大；而obj3、obj4没有出现这种现象。从表2、表4识别结果来看，obj3损伤识别效果均要优于obj1。

相较于obj1，在obj1中引入罚函数的obj2在梁模型中有时会起到提升识别精度效果，但不太明显。而在obj3中引入罚函数的obj4总能取得比obj3好得多的损伤识别效果，这不仅大大减少了误判信息，显著提高了损伤识别精度，而且其识别损伤值标准差更小，即识别结果更加稳定可靠。由此可知：提出的罚函数不适用于目标函数obj1，但适用于obj3；故罚函数与目标函数的不同组合对识别结果有较大影响。