有色噪声下的抗差估计改进算法分析

刘俊钊，李浩军

(同济大学测绘与地理信息学院，上海 200092)

1 引言

GNSS技术的发展极大便利了人类的生产生活，在工程建设、车辆导航、授时同步、跟踪定位等方面都有着广泛应用[1-4]。利用GNSS获取动态目标的实时位置时，常采用卡尔曼滤波建立相应的动力学模型，结合观测数据得到动态目标的最优解，其要求噪声模型具有高斯白噪声特性[5]。然而实际中的观测数据和噪声往往难以满足要求，例如大气延迟的时间性变化使得观测噪声具有时间相关性[6]，而卫星信号受遮挡时则会产生周跳等错误观测信息。噪声的时间相关性和观测粗差使得传统卡尔曼滤波的解算精度受到严重制约。对此，文献[7-8]构造有色噪声和观测方程的组合模型，建立了等效的观测方程，实现对有色噪声的白化。文献[9]采用自适应滤波，利用自适应因子对有色噪声数据权重进行动态调节，实现对有色噪声的整体控制。但当观测数据中含有粗差等情况时，自适应因子的选取将会产生偏差，从而使得计算结果异常。针对观测数据含有粗差问题，许多学者提出相应的抗差估计方法。文献[10]将粗差纳入函数模型，利用均值漂移法得到粗差估值，再对观测数据进行剔除或修正处理。文献[11]基于等价权思想，提出了IGG抗差估计方法，此后发展了IGGII、IGGIII抗差方法，取得了广泛应用。文献[12]提出了改进的双因子抗差方案，通过设置降权临界值，判断观测量的粗差可疑性，对超出临界值的观测量单独降权，避免正常观测量的错误降权。文献[13]分析了有色噪声各历元间的相关性，推导出相邻历元噪声相关的抗差卡尔曼滤波，实现了对有色噪声的控制并具有良好的抗差性，提高了滤波的估计精度，但该方法不能有效处理包含高阶项有色噪声和多粗差的观测数据，算法适用性受到制约。对此，本文首先给出了相邻历元噪声相关滤波的基本原理，分析了有色噪声非相邻历元间的相关性，针对噪声协方差模型进行了改进，基于最小方差准则推导了改进的多步历元噪声相关滤波，最后同文献[12]中的抗差方案结合，通过仿真与传统卡尔曼滤波及文献[13]算法比较，得到了稳定的滤波估计结果，证明了算法的正确性和有效性。

2 相邻历元噪声相关滤波基本原理

传统线性离散卡尔曼滤波的状态模型和观测模型可表示为[14]

(1)

式中，Φk|k-1为k-1历元的状态转移矩阵，Bk为观测系数矩阵，Ωk-1为k-1历元的状态噪声，Δk为k历元的观测噪声，噪声Ω和Δ须满足高斯白噪声特性。

当动态模型的数据包含有色噪声，且状态噪声Ω和观测噪声Δ之间不具相关性时。假设k历元状态噪声Ωk仅与相邻历元的Ωk-1和Ωk+1存在相关性，不相邻的Ωk-1、Ωk+1间互不相关，对于观测噪声Δk-1、Δk、Δk+1同样满足假设。此时，相邻历元噪声相关下的噪声协方差矩阵为分块三对角矩阵[15]，可定义为

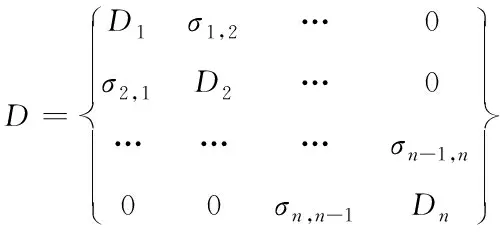
(2)

其中，D1，D2，…，Dn为噪声的自协方差，σ1，2…σn-1，n为相邻历元噪声的协方差。

现定义k-1历元的状态一步预测值为

Xk|k-1=Φk|k-1k-1

(3)

当相邻观测噪声历元相关时，存在

=(I-Jk-1Bk-1)Xk|k-1+Jk-1Lk-1

=(I-Jk-1Bk-1)Xk|k-1+Jk-1(Bk-1Xk-1+Δk-1)

(4)

由协方差传播定律得到观测噪声和状态一步预测值间协方差：

(5)

若相邻状态噪声历元相关，则式(4)可转化为：

=(I-Jk-1Bk-1)Xk|k-1+Jk-1Lk-1

=(I-Jk-1Bk-1)(Xk-1-Ωk-1)+Jk-1Lk-1

(6)

由此得到状态噪声和状态估值间协方差

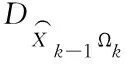
=(I-Jk-1Bk-1)DΩk-1|k

(7)

由式(5)和式(7)可知，当模型中存在有色噪声时，动态系统的状态值与状态噪声及观测噪声存在相关性，协方差不为零，故不能直接采用传统卡尔曼滤波公式进行计算。

最后将式(5)和式(7)分别代入卡尔曼滤波预测协方差矩阵和增益矩阵中，得到相邻历元噪声相关的卡尔曼滤波方法。

3 多步历元噪声相关滤波新算法

3.1 改进的多步历元噪声相关滤波

相邻历元噪声相关滤波认为相邻的历元噪声间存在相关性，计算了相邻噪声间协方差，并代入状态协方差矩阵中一同滤波。该过程简化了噪声的协方差模型，忽略了非相邻历元间相关性，在相关性弱的低阶噪声模型，如一阶AR模型中可取得较好的处理结果。在实际情况下，动态模型中的噪声普遍具有更为复杂的相关性，其非相邻历元间协方差数值较大在滤波过程中衰减缓慢，不可被忽略。为改善这一情况，基于此方法，本文设计了多步历元噪声相关的改进算法。

考虑到实际噪声中各历元间皆存在相关性

(8)

因此，式(2)中的噪声协方差矩阵应改进为

(9)

首先，状态估值的递推表达式定义为

k=Hk-1k-1+JkLk

(10)

定义估计状态误差

εk=Xk-k

(11)

将式(1)(10)代入式(11)中，计算等式两侧期望，顾及E(Wk)=0、E(Vk)=0，可得

E(εk)=(I-JkBk)Φk|k-1E(εk-1)

+[(I-JkBk)Φk|k-1-Hk-1]E(k-1)

(12)

Hk-1=(I-JkBk)Φk|k-1

(13)

将式(1)(10)(13)代入式(11)得到估计状态误差的递推表达式：

εk=(I-JkBk)Φk|k-1εk-1+(I-JkBk)Ωk-1-JkΔk

(14)

令εk|k-1表示预测状态误差

εk|k-1=Xk-Xk|k-1

(15)

将式(3)(13)代入式(10)，得到k历元下状态估值表达式：

k=Xk|k-1+Jk(Lk-BkXk|k-1)

(16)

将式(1)(3)代入式(15)可得

εk|k-1=Φk|k-1εk-1+Ωk-1

(17)

令Dk|k-1表示k-1历元预测状态协方差，Dk-1表示状态估计协方差，根据协方差传播定律得到

(18)

由式(14)得出k-1历元εk-1的递推表达式，随后将其展开为由全局状态噪声、观测噪声构成的函数表达式。令状态噪声与观测噪声互不相关，则存在

(19)

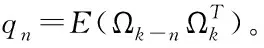
将式(16)代入式(11)得到k-1历元预测状态误差同k历元估计状态误差的表达式：

εk=(I-JkBk)εk|k-1-JkΔk

(20)

故k历元的估计状态协方差为

=(I-JkBk)Dk|k-1(I-JkBk)T

(21)

展开式(17)得到预测状态误差与观测噪声间的线性函数，由协方差传播定律可得

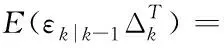
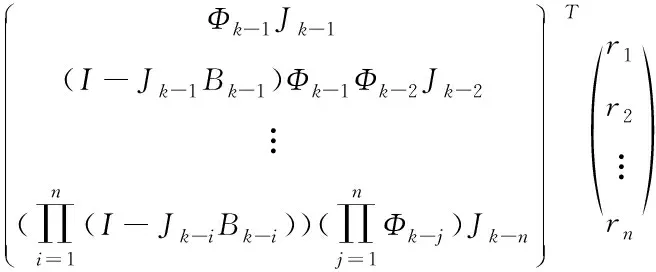
(22)

当增益矩阵Jk满足状态估计方差最小时，得到

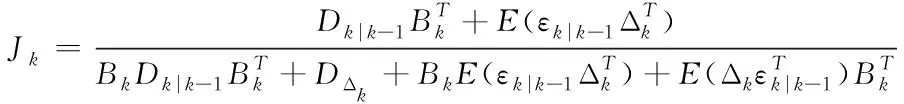
(23)

将式(23)代入式(21)，整理得到

(24)

由此可得多步历元噪声相关滤波的表达式

(25)

3.2 改进的抗差卡尔曼滤波

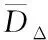
V=B-L=(I-BN-1BTP)∇=R∇

(26)

然而文献[12]中参数kt被直接设定为k0与k1的平均值，实际上k0与k1本身由显著水平决定，而kt的不当选取将使得正常观测量仍存在被错误降权的风险，同时算法的计算效率也将受其影响。鉴于标准化残差序列服从τ(n-t-1)，故本文以参数k0和k1对应的显著水平α0与α1的平均值为依据[16]，从而确定临界值kt的大小，抗差方案的流程如图1所示。

(27)

图1 抗差方案流程图

4 算法案例分析

现假设目标实体在二维平面内匀速运动，系统状态为x，y轴方向的位移和速度，采样间隔为1s，建立卡尔曼滤波运动模型。为验证改进算法的有效性，本文设计了两部分数值仿真，采用传统卡尔曼滤波、文献[13]算法、本文算法三种方法进行对比分析。第一部分针对不同复杂程度的有色噪声按上述三种方法滤波，第二部分在有色噪声的基础上加入粗差后滤波，最后分别比较三种方法得到的状态估值精度。

4.1 有色噪声实验分析

为检验三种方法在动态模型含有不同复杂程度有色噪声时滤波的解算效果，设定以下两种方案进行分析：

方案一：噪声模型为AR模型，状态噪声和观测噪声表达式为Ωk=aΩk-1+ωk-1，Δk=aΔk-1+ηk-1，式中a=0.8，ω～N(0，1)，η～N(0，1)。

方案二：噪声模型为ARMA模型，其表达式为Ωk=mΩk-1+ωk-nωk-1，Δk=mΔk-1+ηk-nηk-1，式中m=0.8，n=0.5，ω～N(0，1)，η～N(0，1)。

设定历元时间为1000s，分别采用三种方法按上述两种方案进行一次滤波，计算状态估计真误差，随后进行200次蒙特卡洛仿真，计算每一历元时间的位移均方误差(RMS)。图2和图4分别给出了两种方案下三种方法的位移真误差结果。图3和图5则分别给出两种方案下三种方法200次仿真的位移RMS。表1为两种方案下三种方法的位移RMS平均值。

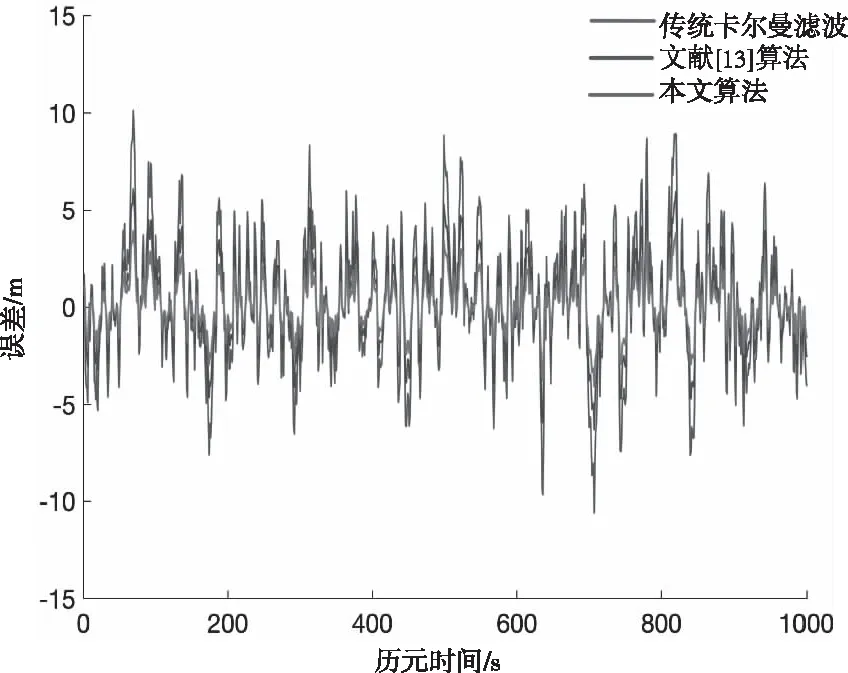
图2 方案一中三种方法位移误差

图3 方案一中三种方法位移RMS

由图2可知，受方案一中有色噪声的影响，传统卡尔曼滤波难以有效控制噪声对动态系统的扰动，即便是匀速运动模型，位移误差可达10m，这是由于其噪声模型被定义为不具相关性的白噪声，因此该方法在实际应用中将受到严重制约。文献[13]算法的结果优于传统卡尔曼滤波，位移误差显著减小。本文算法的结果则优于文献[13]算法，误差进一步缩小，位移误差被有效控制在5m以内，可见本文针对噪声协方差模型的改进能够提高滤波的解算精度。

由图3可见，三种方法的RMS变化都较为平稳，反映出滤波过程的有效性，文献[13]算法和本文算法的变化曲线较传统卡尔曼滤波振幅更小，说明了两种方法能够减弱有色噪声对状态估计的扰动，滤波过程更加稳定。从表1可以发现，在方案一中，相比于传统卡尔曼滤波，本文算法的RMS平均值更小，滤波精度更高；相比于文献[13]算法，本文算法的RMS平均值为1.7429，小于其2.1159，滤波精度有所提高。

图4 方案二中三种方法位移误差

图5 方案二中三种方法位移RMS

对比图2中结果，图4采用方案二噪声模型后，传统卡尔曼滤波的位移误差曲线振幅进一步增大，滤波精度下降，这是由于ARMA模型的有色噪声对状态系统扰动更大，传统卡尔曼滤波不能借助原有的白噪声函数模型实现对状态值的准确估计，大量的噪声被直接传递到状态估值中。文献[13]算法虽有所改善，但差异不大。本文算法中的位移误差仍被控制在5 m以内，优于其它两种方法。可见本文算法能够控制相关性更为复杂的有色噪声，在实际应用中具有更好的适用性。

表1 两种方案下位移RMS平均值

由图5和表1可知，受ARMA模型噪声的影响，三种方法RMS平均值增大，滤波解算精度降低，而本文算法精度始终优于其它两种方法，且本文算法的RMS曲线振幅较传统卡尔曼滤波和文献[13]算法更小，滤波稳定性更高。

4.2 有色噪声下的抗差实验分析

在4.1节实验的基础上，设定有色噪声为ARMA模型，对第150、350、550、750和950历元共5个点位添加5～10倍中误差。选取显著水平α0=0.1，αt=0.05，α1=0.001，得到本实验中的临界值k0=1.25，kt=1.34，k1=1.41。采用上述三种方法进行滤波实验，首先对5个点位的x方向位移添加20m粗差，此后在y方向位移添加30m粗差。

图6给出了x方向存在粗差时三种方法位移真误差的变化曲线，其中5个点位的x方向误差值见表2。图7给出了x、y方向存在粗差时位移真误差的变化曲线，其中5个点位的x方向误差值见表3，y方向误差值见表4。

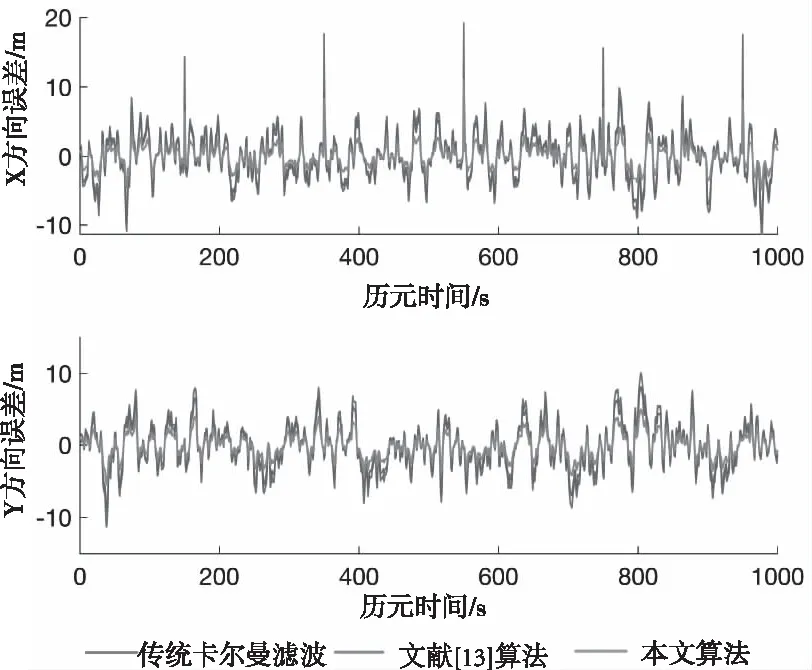
图6 x方向存在粗差

图7 x、y方向存在粗差

由图6可见，在不含粗差的点位中，本文算法得到的x、y方向位移真误差小于其它两种方法，这说明本文算法能够减弱有色噪声对状态估计的影响，而在含有粗差的点位中，位移估值误差受粗差影响较有色噪声更为明显，因此算法的抗差性能将影响最终的解算精度。结合表2可知，在设定的5个粗差点位中，传统卡尔曼滤波的x方向最大位移误差可达19.218 m，文献[13]算法和本文算法的位移误差较传统卡尔曼滤波显著减小，说明两种方法都能实现对粗差的抵抗，提高数据处理精度。

表2 单个粗差下位移误差

由图7可见，三种方法在含有粗差的点位中x、y方向的位移误差明显增大。由表3和表4可知，对于误差最大的1号点位，传统卡尔曼滤波在x方向上误差可达18.7959 m，y方向上误差可达27.1633 m；文献[13]算法x方向误差为9.6799 m，y方向为11.2728m，精度得以提高；本文算法的x方向误差8.5521 m，y方向误差9.8195 m，滤波精度较文献[13]算法有所提升。说明了多个粗差条件下，本文算法可实现对多个粗差的单独降权，进而减弱粗差间相互影响对降权过程的干扰，确保滤波的解算精度。

表3 多粗差下x方向位移误差

表4 多粗差下y方向位移误差

5 结论

针对实际应用中的观测数据包含复杂有色噪声和粗差导致卡尔曼滤波精度降低，本文提出一种改进的有色噪声抗差卡尔曼滤波，从有色噪声和抗差两方面对算法进行了实验分析，通过与传统卡尔曼滤波和文献[13]算法对比后发现：①当状态噪声和观测噪声为ARMA模型噪声时，文献[13]算法的解算精度较传统卡尔曼滤波有所提升但差异不大。本文算法则考虑了有色噪声非相邻历元间的相关性，改进了滤波增益矩阵和协方差矩阵，能够减弱有色噪声的对滤波过程的扰动，提高状态估计的精度。②在受单个粗差影响下，本文算法较文献[13]算法的抗差略有提升，而在多个粗差影响下，文本算法通过对最大标准化残差进行可疑性判断并单独降权，削弱了多粗差的相互影响，提高了算法的抗差性。