120 t LF炉液压比例控制系统研究

李 辉

(大冶特殊钢有限有限公司，湖北 黄石435001)

0 前言

LF精炼炉是通过石墨电极与钢液之间作用产生的电弧作为热源对金属加热冶炼的设备。要保证精炼炉能够持续高效运行，就要维持电弧长度的恒定，从而减少电流波动，故电极升降控制系统在精炼过程中至关重要。一直以来研究者针对如何最大限度改善电极控制系统调节作用，缩短精炼周期、减小电能消耗量等问题投入大量精力进行研究。此外，电弧炉炼钢的电极调节问题一直都是国内外学者非常关注的问题[1-2]。目前电极控制系统还存在很多的问题，比如电极折断现象严重，为了避免折断，通常操作人员会根据以往的经验来提起电极；但是对于国外引进设备，由于其系统不开放、维护性差，会产生“黑箱”问题，使得在处理设备故障、优化控制功能以及改造其他相关设备等方面造成极大障碍；此外，国产设备与国外引进设备在性能上还存在着一定差距，常出现电极工作时噪声大，电极臂柱剧烈晃动，炼钢吨耗电量增加，以及电网电流易引起波动等现象[3]。

目前，LF精炼作为重要的钢铁精炼手段，其电极调节系统工作性能是否优越最终导致电耗的大小和产能。故针对LF精炼炉的电极调节系统进行深入研究具有一定的应用意义[4]。目前LF精炼炉的电极调节系统通常采用的PID调节，无法有效发挥电极调节系统的优势。本文采用智能控制策略研究LF精炼的电极调节系统，在建模方面，通过对大量数据进行不断地训练学习，通过大量的自学习调整参数，在提高产能的同时最大程度的降低能耗[5]。

1 电极控制系统结构及作用

1.1 LF炉电极升降装置结构及作用

电极升降装置是LF炉的关键设备，其设计及制造水平直接影响到生产运行的电耗、电极消耗、三相功率平衡及整机电效率等指标。装置中导电横臂为供电主回路的主要环节，大电流载体，作业率高、工况恶劣，长期以来一直是电炉设备生产运行过程中故障率较高的设备，直接影响LF炉的运行可靠性、维护成本及热停工时间。横臂采用箱式结构的铜钢复合导电横臂，铜钢复合导电横臂(全水冷)电流密度 ≤4 A/mm2。为了保证横臂具有足够的热态强度及刚度，需对其进行强制水冷处理。电极升降装置主要由横臂、立柱装置两大部分组成。横臂由三套电极夹紧放松机构、三套铜钢复合导电横臂、三个水冷铬青铜夹头、电极喷淋装置、全套金属软管及绝缘件等组成；立柱装置包括立柱及与横臂联接的全套绝缘件、紧固件、电极升降液压缸、水路用管线及管件等。

1.2 LF炉液压系统结构及作用

LF炉液压系统包括LF-120t钢包精炼炉液压系统供电极的升降、包盖的升降、电极放松动作。本液压系统包含：(1)给主泵提供动力的主电机、恒压变量柱塞泵、使液压油循环过滤并使液压油冷却的循环系统、油液存放的油箱及相关液压附件等；(2)控制回路滤油器，调压回路、电极升降回路、电极夹紧放松回路、LF炉盖升降装置回路等控制阀件；(3)蓄能器组。其中各液压动作均采用滑阀，动作平稳并且冲击小，液压系统结构简单，各单元逻辑控制条理更为清晰，生产运行过程中故障的分析及排除更为容易，这样在保证运行可靠性的前提下，更为节省投资。

1.3 LF炉电极的作用

LF炉是通过大功率的交流电让电极得电后，使钢水与石墨电极之间产生温度高达几千甚至上万度的高温电弧，作为热源来加热钢水[6-7]。

LF炉电极控制系统如图所示，其由变压器、电极控制盘、短网、伺服阀及升降机构等构成，如图1所示。

图1 LF炉电极控制系统

在电极加热系统中，电流、电压设定值为其最重要的参数之一。在整个加热过程中须将电能消耗、耐材消耗、加热效率等因数考虑在内。合适的电流值不仅能充分发挥设备的能力，还可以迅速提升钢水的升温速度。

当前多数情况下，均是通过估计实际负载值来确定相关电压与电流曲线，其中变压器一次侧压降、短网电阻、变压器二次侧压降、短网感抗、最大视在功率、短网功率因数等非常关键值。在实际生产中，电弧阻抗不是一个常数。通过控制电极的快速反应工作与调节，使加热效率最优化。

2 电极升降液压系统设计

2.1 120t-LF精炼炉电极升降回路控制系统

系统利用液压缸来完成电极的升降，通过实时对现场电弧电流、电压对比设定值，将差值放大传给比例阀线圈[40]。从而通过调整电极使电压调整。

液压式电极调节系统结构如图2所示。

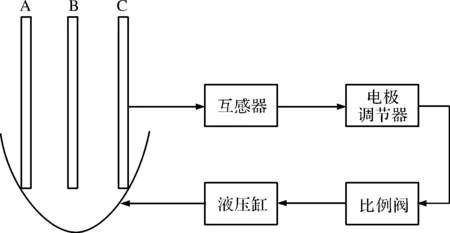
图2 液压式电极调节系统结构图

2.1.1 液压式电极升降回路系统结构

LF炉液压式电极调节系统主要由工业计算机、压力表、比例阀、单向阀、过滤器、油缸、油泵、溢流阀、电极和储能器构成，其工作原理如图3所示。同电弧系统不一样的是用于液压式传动调节系统的电极传动系统无需配重。水、油、乳化液均可作为该系统比例阀的载能液体，这些载能液体的调节响应速度高，便于控制。

图3 LF炉载能液体调节系统结构图

2.1.2 流体调节电极升降控制回路系统架构

流体式调节电级方法有更快速的反应速度，输出的功率比其它方式大等优点[8-9]。其具体工作方式：将电弧电流、电弧电压分别送入后计算比较，通过比例阀调节电极，从而达到控制整个系统的效果。

3 LF炉电极升降系统数学建模

通常将实际液压系统抽象成相近工况情况下的物理模型进行分析，物理模型能够反应出实际液压系统的某些特性，并且更简化，更便于对其进行研究。建立物理模型后，应假设模型的边缘条件，并提供各工况条件对应的系统内部参数及其相互作用关系。该液压系统的非对称液压缸(单出杆缸)的动力机构采用对称伺服阀控制。图4为非对称油缸组成的动力机构。

图4 控制系统物理模型

3.1 伺服阀信号电流和弧长增量间的关系

弧压增量ΔUh和弧长增量ΔH之间关系为

ΔUh=βΔH

(1)

式中，β为电弧压降梯度，随熔炼时间改变，熔化期较大，精炼期较小。

弧流增量ΔUh和弧压增量关系为

(2)

式中，Z—变阻器的单相总阻抗。

平衡电阻R1和R2的电压分别与弧电流及弧电压可用以下线性方程表示：

u1=B1Ihu2=B2Uh

(3)

式中，u1为平衡电阻R1的电压；u2为平衡电阻R2的电压；B1为电流互感比与调压器变换比常数；B2为隔离变压器的变换比常数。

伺服阀中的信号电流 根据克希霍夫定律,可表示为

Isv=A1u1-A2u2

(4)

联立式(1)～(4)；可得

Isv=K1ΔH

(5)

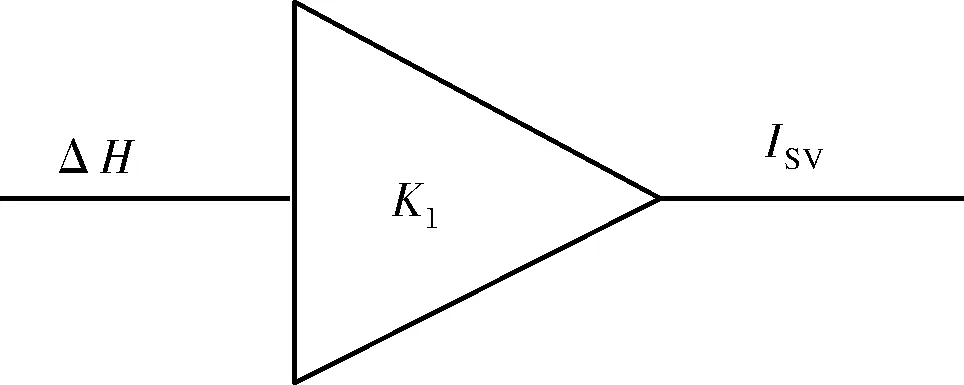
图6 高度控制系统方框图

3.2 弧长和油缸位移之间的关系

LF炉熔炼是物料从固态逐渐熔为液态的过程。由于固态物料表面存在不均匀现象，易产生物料变形，使电弧拉长后断裂，电极液压系统快速调整杜绝上述两种情况产生。电极在加热物料过程中必然会逐渐消耗缩短，因此必须通过电极液压系统实时调节电极升降长度。图7为电弧与液压缸位置关系图。

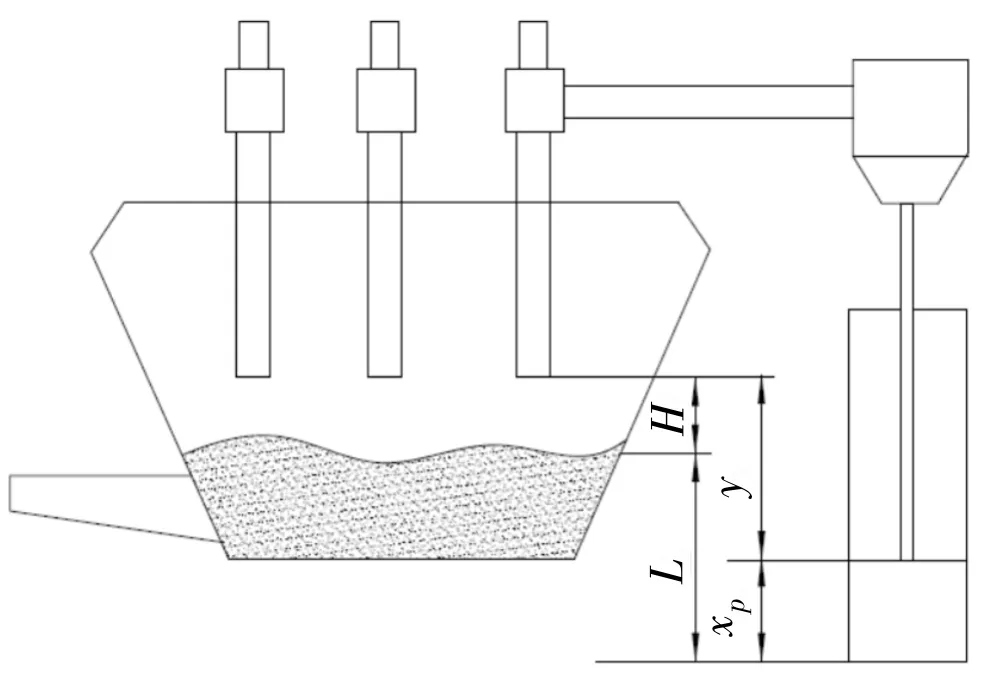
图7 电弧炉液压缸位置关系

由图可知，

H=xp+y-L

(6)

式中，H为弧长；xp为活塞油缸位移量；y为电极的烧蚀量；L为电极下物料的标高。

由式(6)可知，LF炉弧长受油缸位移控制。电极烧灼量和物料高度为系统外界干扰，烧灼量可近似等效为等速输入信号，物料高度可看做阶跃输入信号。

3.3 液压缸模型的建立

3.3.1 活塞杆收缩情况(xv≥0)

(1)滑阀的流量方程。假定本系统采用四个匹配对称的节流窗口，零开口四边滑阀，进油压力定值，无压回油。伺服阀进、回油腔的流量方程可表示成。

(7)

(8)

式中，q1为进油腔流量，m3/s；q2为回油腔流量，m3/s；ρ为液体的密度，kg/m3；Cd为流量系数；p1为油缸活塞杆腔的压力，Pa；p2为油缸活塞腔的压力，Pa；ps为系统压力，Pa；xv为伺服阀油量控制行程，m；xp为活塞位移，m；W为伺服阀窗口的面积梯度，m；A1为油缸有杆腔活塞有效面积，m2；A2为油缸无杆腔活塞有效面积，m2；

(2)流量连续性方程。假设油缸油管很短且所有工作腔压力相同。视油缸体积、油温弹性模量为常量，漏量为层流流动。

油缸进油口流量可表示为

(9)

液压缸回油口流量可表示为

(10)

式中，V1为油缸活塞杆腔容积，m3；V2为油缸；活塞腔容积，m3；

Cip为工作油缸内泄漏系数，m5/(N·S)；Cep为工作油缸外泄漏系数，m5/(N·S)；βe为工作体积的弹性模量，Pa。

当油缸处于稳态时，力平衡方程

N=p1A1-p2A21

负载流量方程可表示为

(11)

(3)液压缸的工作平衡。所有外力包括惯性力、弹力、粘性阻尼力及其它外力(本课题主要包括横臂和电极的自重)。液压缸负载力和输出力的平衡方程可表示为

(12)

式中，FL为外力；K为负载的刚度；Bx为活塞及受外力的粘性阻尼系数；mt为活塞及受外力的总质量，kg。

(4)伺服阀负载流量线性方程。利用泰勒公式将式(7)在系统其中一个工作位置附近展开(忽略高阶无穷小情况)，将压力—流量特性方程线性化，对系统进行线性化动态分析，可得：

ΔqL=kqΔxv+kcΔpL

(13)

分别对式(11)、式(12)和式(13)进行拉氏变换，可得

QL=kqxv-kcpL

(14)

(15)

N=A1pL=m1s2Xp+BpsXp+KXp+FL

(16)

联立式(14)、式(15)和式(16)可得

(17)

式中，kce为总流量-压力系数，kce=kc+Cte；Qtu为附加泄漏流量，Qtu=CtePs。

动态方程(17)是一个很常用的表达形式，其中附加泄露流量影响很小可忽略不计。由粘性摩擦所引起的泄漏而产生的活塞速度比活塞的运动速度小很多加之粘性阻尼系数Bp也很小，故在K=0时，可将式(17)可简化成：

(18)

式中，ωh为液压固有频率；ζh为液压阻尼比。

当考虑Bp影响很小时,ζh可表示为

指令输入Xv的传递函数可表示为

(19)

干扰输入FL的传递函数可表示为

(20)

3.3.1 活塞杆收缩情况(xv≤0)

xv≤0的建模过程与xv≥0过程类同，本文不再赘述，其中几个主要关键系数如下。

3.4 电液伺服阀输入信号电流至主滑阀之间的传递函数

利用电液伺服阀作转换元件组成的闭环系统称为电液伺服系统。它能将弱电信号转换成大功率液压信号流量和压力。液压元器件重量轻，惯量小，因此精度较高。利用电信号作为反馈信号和控制信号的好处在于其反应迅速，操作快捷。电液伺服阀自身是一个多级放大的闭环电液伺服系统，其不仅是液压执行机构的控制元件，同时也是液压系统的信号转换和功率方法元件。电液伺服系统由于其控制精度高、响应快的特点，在生产设备、军事、交通运输等方面得到广泛应用。

将伺服阀动态特性非线性方程通过线性化处理，得到伺服阀传递函数，进而对系统进行线性化研究，尤其是对系统稳定性的线性研究。伺服阀利用二阶震荡环节的传递函数可以保证其精度，当动态响应在负载响应10倍以上时，可以将伺服阀等效成比例环节。

伺服阀的二阶等效传递函数可表示为

(21)

式中，Wsv(s)为伺服阀的二阶传递函数；ωsv为频宽(rad/s)；ζsv为阻尼系数，一般为0.5～1；ksv为阀增益，假设输入为电流IN、输出为阀芯位移Xv时，ksv=Xv/IN。

3.5 LF炉电极升降液压伺服系统总方框图

(1)如图7为液压的伺服系统控制图。

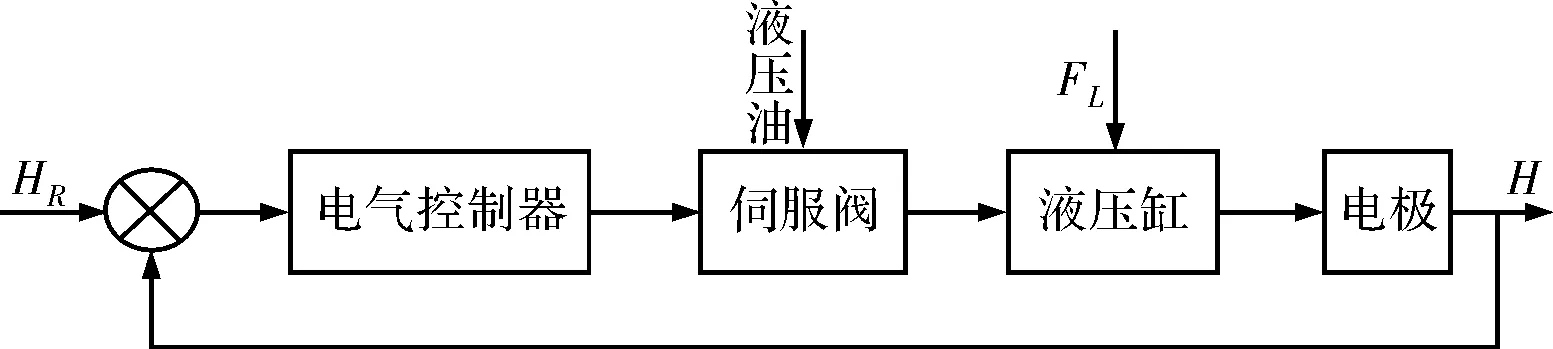
图7 系统控制方程

(2)当xv≥0时，图8为液压缸系统模型方框图。

图8 时系统模型方框图

(3)当时当xv≤0时，图9为液压缸系统模型方框图，

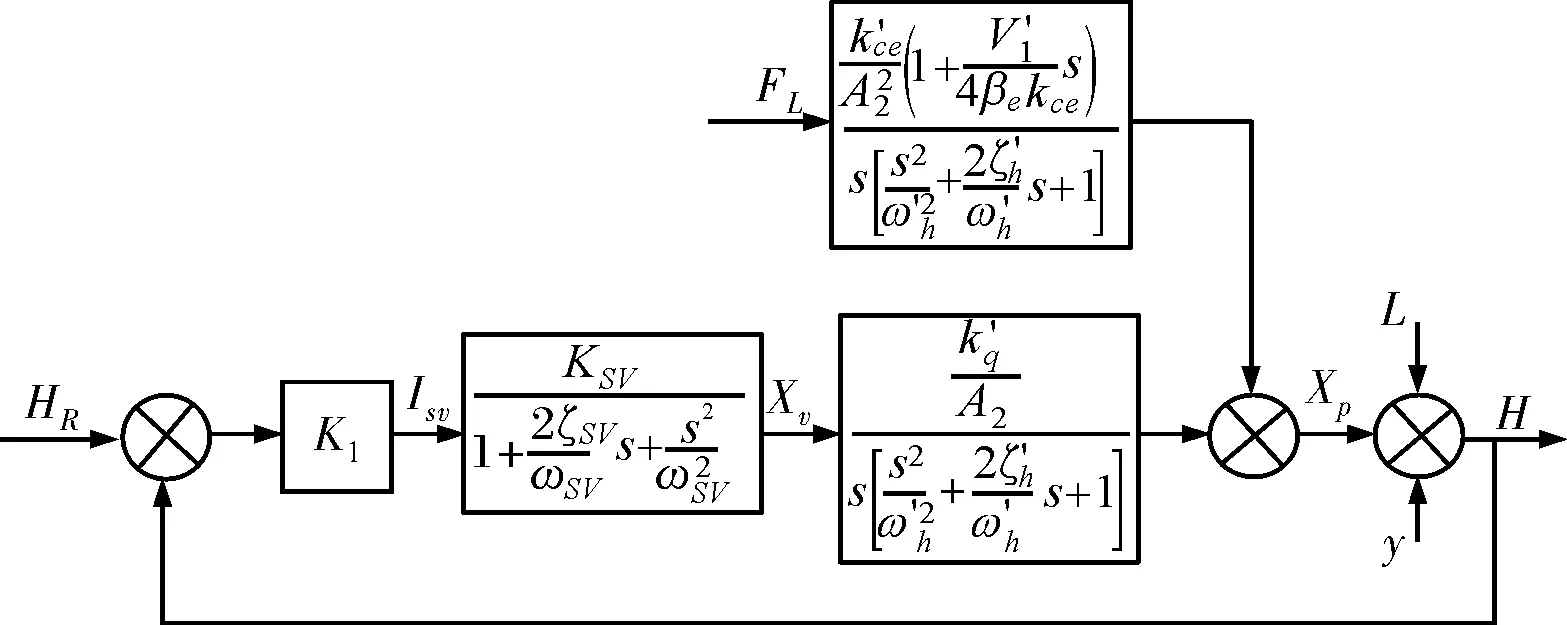
图9 时系统模型方框

4 电极升降系统模型的仿真与分析

4.1 液压系统模型参量选取

4.1.1 液压油参数选取

本文中液压缸工作介质选择N46#液压油，详细参数见表1。

表1 液压油参数表

4.1.2 电极升降液压系统原理

(1)电液伺服阀的参数选择

本系统选用的伺服阀型号为SV10-F200NF，额定流量为qn=250 L/min，伺服阀的空载流量q0=qn=250 L/min，选取流量系数Cd=0.28，阻尼系数ζsv=0.6；系统油源压力己知为Ps=12 MPa，IN=300 mA，Xvm根据阀最大行程取Xvm=80 mm。

2)液压缸的参数确定

通过代入前面公式计算得到以下结果：

(3)比例环节的参数选取

将相关参数选用，取K1=0.8。

4.2 液压系统动态特性原理

利用表 2中的相关系数带入系统开环传递函数，利用MATLAB软件进行开环波德图仿真，结构如图10所示

表2 液压缸模型参数表

图10 位置控制系统开环波德图

由图10得到，相位稳定裕度大于30°，本控制系统复值稳定裕度大于6 dB。复值稳定裕度在20>Kf>6 dB之间，相位稳定裕度在60°>Kf>30°之间才满足要求。反观该系统的这两个数值相对偏大，故可通过PID对其进行改进。

4.3 伺服系统闭环响应特性原理

本研究利用MATLAB/SIMULINK建立闭环系统仿真模型仿真计算闭环系统的响应特性。

当输入阶跃信号时，仿真得到图11和图12.

图12 xv≤0系统阶跃信号响应曲线

当输入正弦信号时，得到图13和图14。

图13 xv≥0，系统正弦信号响应曲线

图14 xv≤0，系统正弦信号响应曲线

从响应曲线可以看出，xv≥0时响应时间达到了5 s，xv≤0时响应时间约为4 s，通过正弦响应曲线看出系统跟踪曲线有滞后。系统可以利用控制器进行调整。

4.4 外界对系统性能的干扰

外界干扰都包括外负载力FL，电极烧蚀量y、炉内物料标高L等，其中每个影响因素的解析如下。

4.4.1 外负载力对系统性能的影响

当外界负载力为FL=120 000 N时，炉内物料标高L和电极烧蚀量y均设置为为零，忽略两者对系统稳定性的影响，得到系统阶跃信号响应曲线如图15所示。

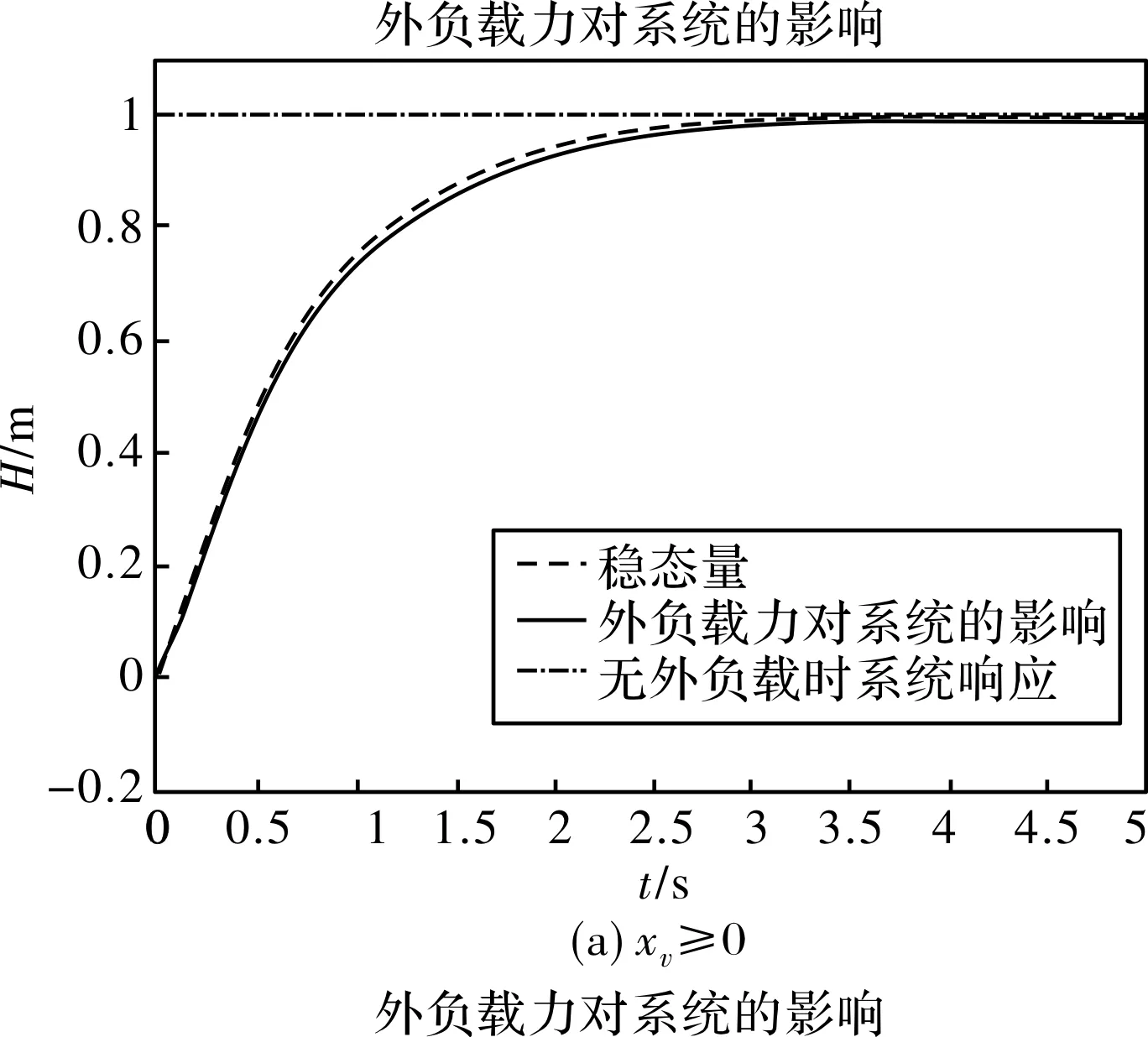
图15 加入外界负载力的系统阶跃信号响应曲线

通过对上述曲线分析可以看出外界负载力对原曲线的跟踪性比较好。同时可以看到，受外界负载力影响以后的曲线在4 s以后基本与原曲线重合，充分说明本系统抗干扰能力较强，进入稳定状态快。

4.4.2 炉内物料标高的影响

阶跃式变化为炉内物料标高的主要变化形式：

(22)

将外界负载力FL和电极烧蚀量y设置为零，设炉内物料标高L以0.1 m/s的速度变化，并对该种情况下的系统阶跃信号响应曲线与未加干扰的曲线进行比较如图16所示。

图16 炉内物料标高对系统影响的系统阶跃信号响应曲线

结果表面，在炉内物料标高L以0.1 m/s速度变化的曲线与原曲线的相似度较高，抗干扰能力比较好。

4.4.2 电极烧蚀量对系统性能的影响

电极的烧蚀量y可以视为等速变化形式为

(22)

设电极烧蚀量y的斜率为0.1，原曲线同仿真曲线比较如图17所示。

图17 电极的烧蚀量影响系统阶跃信号响应曲线

当xv≥0时，系统超调量虽有些滞后但还是有所增加，但当xv≤0时带干扰曲线同原系统曲线强关联，通过计算得到的曲线可知电极烧蚀量可以有效的抗干扰。

5 总结

通过以上分析可以看出本系统对炉内物料标高L、电极烧蚀量y、外负载力FL均具有较强的抗干扰能力。深受这些因素的影响，系统稳定性尚未出现较大波动。本研究成果对大型LF炉电极升降控制系统的设计提供了重要参考。对其建模分析过程中，只考虑了外负载力、炉内料高水平以及电极烧蚀量这三种因素的影响，后续还应该增加更多设计工况对电极升降控制系统的外界影响因素进行分析，在控制策略上还有很多工作要做。