基于趋势拟合模型的承德市献血人群血清学检测量预测
2022-02-08马清杰常缨张小伟刘明丽
马清杰 常缨 张小伟 刘明丽
目前,输血医学已成为临床医疗救助中不可或缺的手段[1]。根据临床用血随机性与时效性的特点,在随机情况下保证安全血液的供应已成为各个国家面临的一项重要课题[2]。随着现代统计学的发展,各类数学模型被广泛地引入到全人群疾病等方面预测中[3]本研究应用线性规划(linear regression)趋势拟合模型预测未来血站献血者常规血清学检测与HIV阳性(初筛与确证)样本检测量变化趋势。为保证血液安全建立与实验室血液检测业务相适宜的组织结构和人员配备、所需要的仪器与设备配置、试剂与材料的库存管理作出正确的预判[4]。
1 对象与方法
1.1 调查对象 2011年1月至2021年12月承德市中心血站献血者常规血清学检测HIV初筛反应性样本(人份)数据来自本血站计算机信息管理系统(唐山启奥,版本9.5),确证阳性样本(人份)数据来自承德疾控部门反馈数据(人份)。
1.2 方法
1.2.1 趋势拟合模型的原理与建立:时间序列是指把某一变量在不同时间上的数值按时间先后顺序排列起来所形成的序列,它的时间单位可以是分、时、日、周、旬、月、季、年等。时间序列模型就是利用时间序列建立的数学模型,它主要被用来对未来进行短期预测,属于趋势预测法。趋势拟合法是根据时间序列动态曲线的变化情况,可以用相应的函数方程对曲线进行拟合,由样本数据估计出函数方程后,通过该方程求出时间序列各观察值的趋势值。直线模型选择依据:①数据量少;②此年度数据无季节变动影响及周期变动特征。其预测步骤:①绘制观察期数据的散点图,确定其变化趋势的类型;②对观察期数据加以处理;③建立数学模型;④修正预测模型;⑤进行预测。
1.2.2 建立献血者常规血清学检测与HIV阳性样本量的趋势拟合法的时间序列预测模型:①数据资料的收集:将2011至2021年承德市中心血站常规血清学检测与HIV阳性(初筛与确证)样本量数据进行核查、整理、分组、归纳,将数据录入R软件(版本1.2.5033),进行统计分析。②将2011至2021年数据绘制散点图。③线性拟合模型建立:线性拟合公式是y=at+b的形式(a为t是0时的预测值;b为逐期增长量;t为时间,比如年次/月次等,y为预测值)。以酶免总数预测为例,y为阶段t酶免总数趋势值;a为趋势线的截距;b为趋势线的斜率。④改善修正模型和数学模型预测。
1.3 统计学分析 应用R软件进行统计分析。用拟合优度R-square和小误差概率P值检验线性拟合模型的可靠性,以判断拟合优度。在原先模型的基础上修正模型,即将不同年份的统计值进行不同预测权重,或将线性模型变为二次函数模型等方式,以提高模型的拟合优度。对变量进行线性回归分析,采用最小二乘法进行参数估计时,选取最高的R值最高的线性方程进行预测,P<0.05为差异有统计学意义。
2 结果
2.1 献血者常规血清学检测与HIV阳性样本量及发展变化 长期趋势有线性上升趋势,可以进行序列对时间的线性回归分析。通过绘制线图,可以看出常规血清学检测数、初筛反应性总数序列有明显的上升趋势。见表1,图1、2。
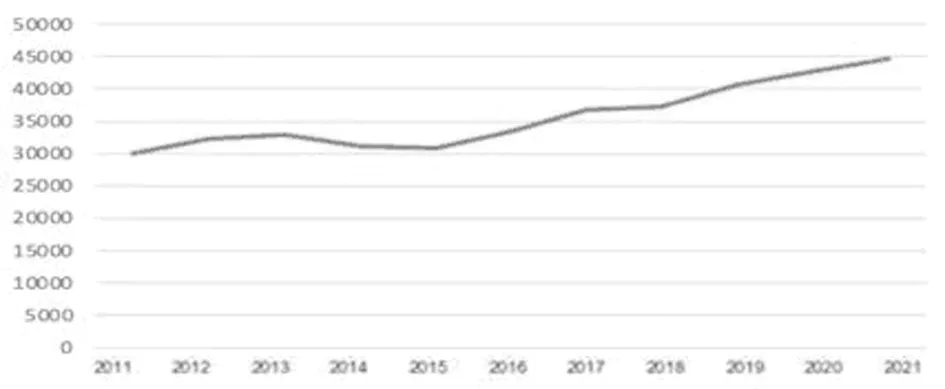
图1 2011至 2021年承德市中心血站献血者常规血清学检测量变化曲线
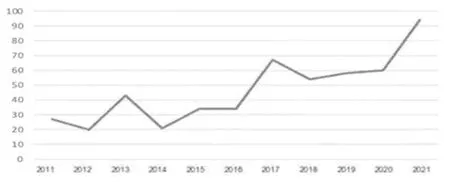
图2 2011至2021年承德市中心血站HIV阳性(初筛)样本量变化曲线

表1 2011至2021年承德市中心血站常规血清学检测与HIV阳性样本量统计表 人份
2.2 线性规划(linear regression)趋势拟合模型的建立
2.2.1 常规血清学检测数拟合公式:R-square为0.86,P=0.00002042 < 0.05。见图3。
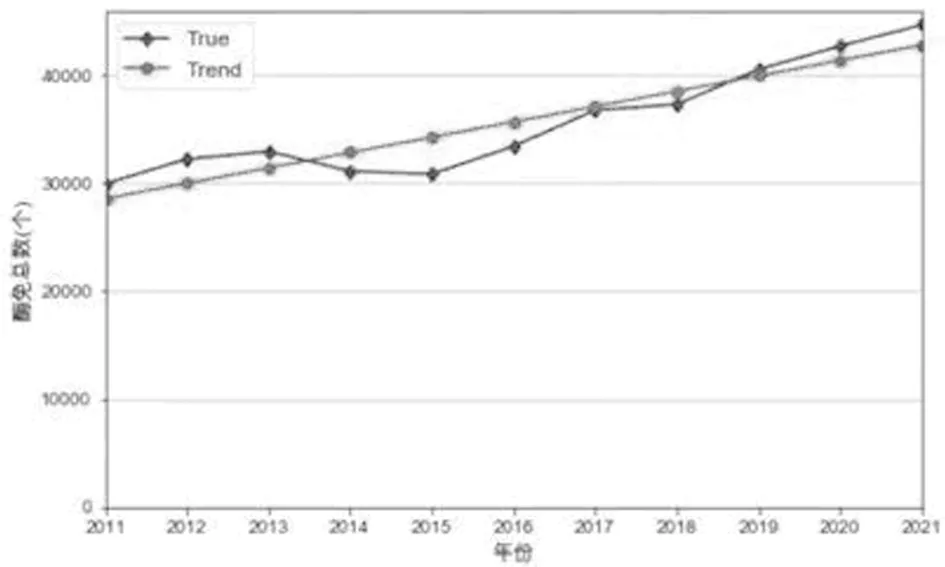
图3 2011至2021年常规血清学检测量线性趋势
2.2.2 HIV初筛反应性总数拟合公式:R-square为0.73,P=0.0008503< 0.05。见图4。

图4 2011至2021年HIV初筛反应性量线性趋势
2.2.3 HIV确证阳性数拟合公式:R-square为0.43,P=0.02894< 0.05。从拟合优度R-square可以看出,模型精确度不够,只能预测趋势,不能预测出准确值。2020年预测值10.6(相对误差为50.0%),2021年预测值11.5(相对误差为15.0%),2022年预测值12.4。见图5。

图5 2011至2021年HIV确证阳性量线性趋势
2.2.4 改善模型:①给年份数据加权重,假设2011年的数据对预测结果的影响最小,前三年数据对预测结果的影响最大,权重比例为:0.05,0.09,0.09,0.09,0.09,0.09,0.1,0.1,0.1,0.1,0.1。以HIV确证阳性数为例,拟合公式:,R-square为0.4,P=0.02688< 0.05,可以看出模型拟合效果改善。②不加权重,改模型为二次线性模型,以HIV确证阳性数为例,拟合公式:,R-square: 0.44,这里可以发现效果还不如线性模型。2020年预测值10.39(相对误差为48%),2021年预测值11.24(相对误差为12.4%),2022年预测值11.54。见图6、7。
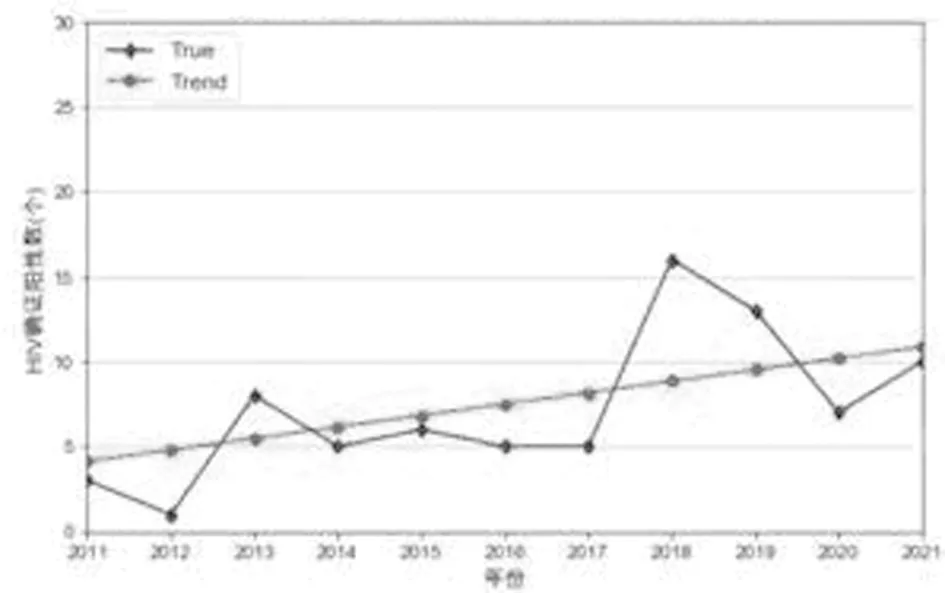
图6 2011至2021年HIV确证阳性量线性趋势(改善模型)
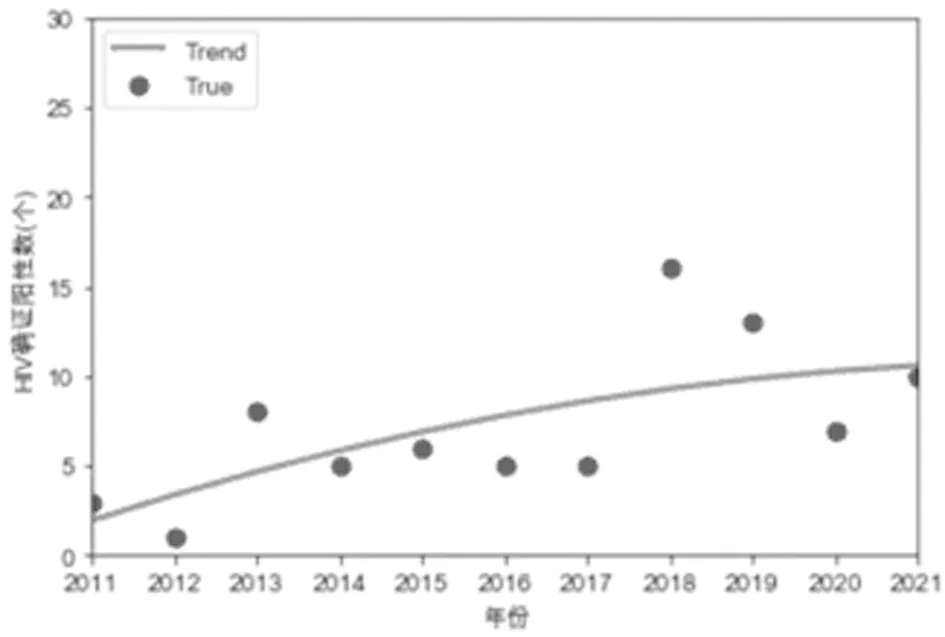
图7 2011至2021年HIV确证阳性量线性趋势(改模型为二次线性模型)
2.3 2020至2022年承德市献血者常规血清学检测与HIV阳性样本量趋势模拟法预测 献血者常规血清学检测量和HIV初筛反应性样本量有逐年持续上升趋势,R值分别为0.86和0.73,均较高,回归拟合效果越好,将2020至2021年的预测值同其真实值比较,其相对误差均较小;该模型的分析预测精度较高,效果良好,可用于对2022年的预测。HIV确证阳性样本数量变化不明显(或无显著性变化)。2022年常规血清学检测为44 251人份,HIV初筛反应性数预测值为81人份,HIV确证阳性数预测值为12人份。见表2。

表2 线性规划趋势拟合模型及预测结果
3 讨论
血液及血液成分的供应是全球范围内值得关注的公共卫生问题之一,保证无偿献血有效供应和血液安全,是采供血系统两项长期并行的重要任务[5]。血站的采供血过程,要确保血液检测结果的正确性,其基础要配备适宜数量的血站实验室血液检测人员、仪器与设备、试剂与材料,同时还需保护医护人员的人身安全与健康[6]。在输血医学领域针对无偿献血者血液检验结果分析的研究较多[7-12],应用于疾病发病率或感染率预测分析的研究方法主要有以下几种:时间序列分析(ARIMA模型、灰色预测法、Markov模型、季节周期回归模型等)、人工神经网络模型、回归分析法及组合模型等。时间序列线性规划(linear regression)趋势拟合模型预测血站系统献血人群血清学检测量尚未见报道。
时间序列线性规划趋势拟合模型是一种重要的时间序列预测方法,其模型比较简单,对资料的要求比较单一,只需变量本身的历史数据,有着广泛的适用性;采用大量的数据逐点分析其走势,作总体计算进行推测[13]。这种方法由细微的分析扩展到宏观的统计,形成规律曲线后再运用到实际的某年、某月,绘制出该月各个阶段的具体走势。客观地说,偶尔出现几次技术差错是难免的,比如数字和日期及时间看错等。但因走势图曲线是由无数个小点连续累积而成,因此,即使某个小点(或某一天)或某几个小点(或某几天)的走势出现偏差了,也不大会影响当月的总规律的准确度[14]。这就如同在某些具体科学实验中,所得数据中常会有少量“坏值”,但它不会对实验的最终结果构成根本性的干扰。本文的趋势分析法的优势就在于此。也就是说,其置信度是经得起实践检验的。我站应用趋势拟合模型预测研究下一年度的献血人群血清学检测量、快速筛查,以及日常联合检测管理[15],有利于指导献血招募工作开展,对降低血液报废率和成本及保障临床用血[16,17],具有积极意义;对血站实验室血液检测仪器设备、试剂物料、人员配备等方面因素提早做出工作计划,使血液检测工作有条不紊、合理有序;对于我站统筹制定检验计划和及时调整血液检测策略,降低检验人员职业暴露风险起到计划性的指导作用,保证血液供应具有重要意义。
