基于FFT-SVD 算法的转子轴心轨迹提纯与故障检测
2022-02-07肖鑫龙杨洪涛郭晓军
肖鑫龙,杨洪涛.2*,陈 贺,郭晓军,李 莉,沈 梅
(1.安徽理工大学 机械工程学院;2.安徽理工大学 矿山智能装备与技术安徽省重点实验室,安徽 淮南 232001;3.无锡市新久扬机械制造有限公司,江苏 无锡 214181)
转子作为重要的旋转机械零件,工作环境一般极为恶劣。在转子工作的过程最容易出现转子不对中故障[1]。转子不对中的原因主要是安装误差、承载后的变形和环境温度的变化[2]。目前,一种方法通过直接对转子振动信号的相位、幅值进行分析,提取故障特征[3-5],另一种方法是通过转子轴向和径向振动信号合成轴心轨迹来识别转子故障[6]。轴心轨迹是转子旋转中心轴相对于轴承座振动位移轨迹,它可以实时反映出转子的工作状态,相比于直接分析振动信号具有更强的分辨性,因此被广泛应用于转子的故障诊断[7]。但在采集转子振动信号过程中往往因为包含大量的噪声而使故障信号特征淹没,很难通过轴心轨迹来识别出转子产生的故障。因此把噪声和干扰信号从原始信号中分离出来对转子故障轴心轨迹的识别至关重要。
现在对轴心轨迹信号进行提纯的算法很多,例如主成分分析(Principal Component Analysis,PCA)[8]、小波 阈值(Wavelet Threshold,WT)[9]、变分模态 分解(Variational Modal Decomposition,VMD)[10]、经验模态分解(Empirical Modal Decomposition,EMD)[11]、数学形态学法(Mathematical Morphology,MM)[12]等。PCA 算法方差小的非主成分可能含有对样本差异的重要信息;WT算法存在各频带间能量交叠的现象;VMD算法会随着时间的推移在全局范围内造成信号重叠;EMD算法会造成信号的模态混叠;MM 算法存在结构元素形状和大小难以选择等问题[13]。
奇异值分解(Singular Value Decomposition,SVD)是一种非线性信号滤波处理方法,非常适合应用于非平稳信号和非线性信号的特征提取。钱征文等[14]通过仿真验证奇异值分解对白噪声和色噪声有较好的降噪效果;张景润等[15]通过奇异差分谱理论清晰的对轴心轨迹进行提纯;郭明军等[16]从能量损失角度提出有效奇异值的选取方法,进一步完善了差分谱理论并对轴心轨迹降噪提纯成功。但是在研究中发现当奇异值差分谱的第二个或者第三个峰值同样很大的时,只通过差分谱选取峰值进行信号重构会造成信号失真,故障特征会和噪声一起被过滤掉。
因此,本文针对转子轴心轨迹存在噪声、干扰等问题,研究了一种FFT-SVD 利用特征频率选取奇异值,对轴心轨迹进行降噪提纯的算法。经实验分析,FFTSVD 算法能有效提纯轴心轨迹,并成功检测出转子不对中故障。和奇异值差分谱、EMD、小波阈值降噪算法相比较,本文研究算法对轴心轨迹的降噪提纯更清晰光滑有效。
1 FFT-SVD降噪原理
图1 为FFT-SVD 降噪原理流程图,首先将采集到的转子轴向信号X和径向信号Y转换为Hankel 矩阵,再进行奇异值分解,对原始信号进行FFT 变换得到频谱图,根据特征频率选取有效奇异值来重构信号,最后将重构后的信号合成轴心轨迹。

图1 FFT-SVD降噪流程图
1.1 Hankel矩阵的构造
假设原始信号为x= [x1,x2, … ,xl],则构成的m行n列的Hankel矩阵X为:
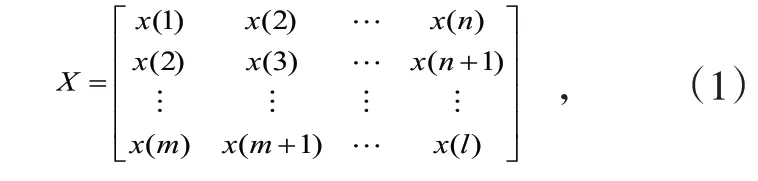
其中l=m+n- 1,研究表明Hankel 矩阵的行数和列数越相近信号提纯的效果越好,因此,当l为偶数时,m=l/2,n=l/2 + 1;当l为奇数时,m= (l+ 1)/2,n= (l+ 1)/2。
1.2 SVD分解
任意实矩阵X Rm n必存在正交矩阵U Rm m和V Rn n使下式成立

式(2)称为X的奇异值分解,其中左奇异矩阵

为X的奇异值个数,12r0。
式(2)可展开为:

或将矩阵U、V写成分量组合的形式
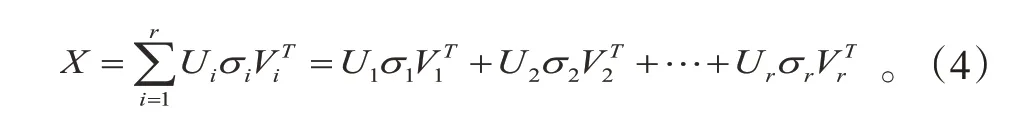
1.3 有效奇异值选取
上述将原始信号x构造成Hankel 矩阵X,假设有r个奇异值,则经奇异值分解得到各分量矩阵如式(5)所示:
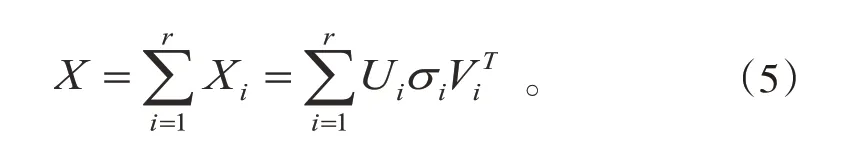
本文通过FFT-SVD 算法利用特征频率选取有效奇异值,假设有效奇异值个数为k,即

1.4 矩阵重构
由以上选取前k个有效分量矩阵进行信号重构,则重构后的矩阵X*为:
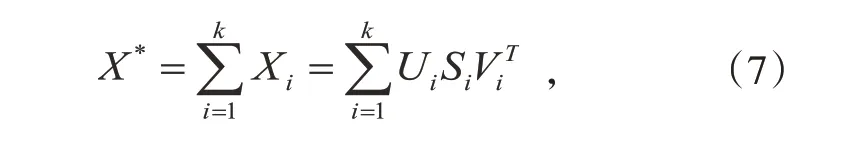
其中左奇异矩阵[U1,U2, ,Uk],右奇异矩阵,奇异值S[diag(1,2, ,k)],则重构后的矩阵为:
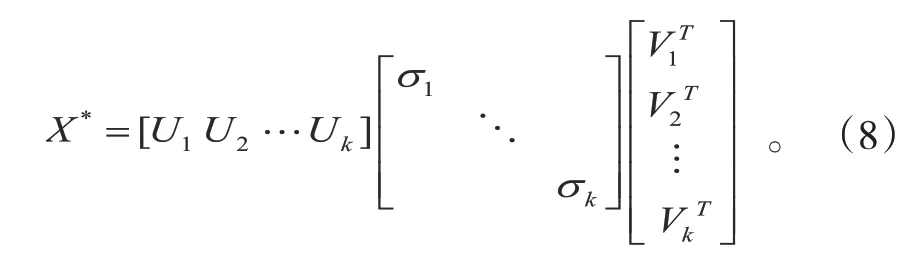
2 实验分析
实验流程如图2 所示,通过搭建转子故障试验台采集转子信号来合成轴心轨迹。

图2 实验流程图
2.1 实验装置
本文研究对象为如图3 所示的转子实验台装置,主要由800 mm*150 mm的实验台体、400 W伺服电机、10 mm 直轴钢、6200 深沟球轴承、可调偏心轴承座、联轴器和负载盘组成。
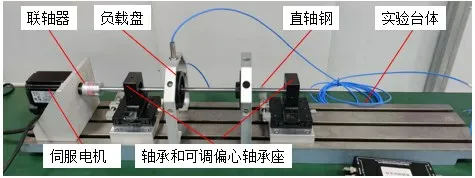
图3 转子实验台装置图
2.2 轴心轨迹数据采集系统
转子轴心轨迹信号采集系统主要由HD9200 数据采集器、2 个WT0150 电涡流传感器、HTX-V3 信号调理器、转速控制箱和上位机组成,如图4 所示。2 个相互垂直的WT0150电涡流传感器安装位置如图5所示,WT0150 电涡流传感器的频率响应为0~10 kHz,灵敏度为8 V/mm,通过采集转子的轴向位移信号X和径向位移信号Y合成轴心轨迹。

图4 HD9200数据采集系统

图5 电涡流传感器安装位置
2.3 模拟转子不对中及信号采集
本实验主要模拟转子不对中故障,通过电涡流传感器采集的转子轴向和径向位移信号,经FFT-SVD降噪提纯后拟合轴心轨迹。其HD9200数据采集系统中信号的采样率为10 240 Hz,采样时间为0.5 s,采样点数为5 120个,电机转速设置为3 000 r/min。
通过调节如图6所示可调节偏心轴承座的不对中距离,来模拟转子不对中,用HD9200数据采集设备采集转子不对中轴向信号X和径向信号Y,如表1为部分信号数据(前15个)。

表1 信号X和Y的部分数据

图6 可调偏心轴承座
2.4 合成轴心轨迹
对实验所采集的转子轴向信号X和径向信号Y,首先画出如图7所示的信号X时域图和Y的时域图,再将信号X和Y合成如图8所示的轴心轨迹图,可见直接通过X和Y合成的原始轴心轨迹杂乱无章,无法通过轴心轨迹来检测转子故障。
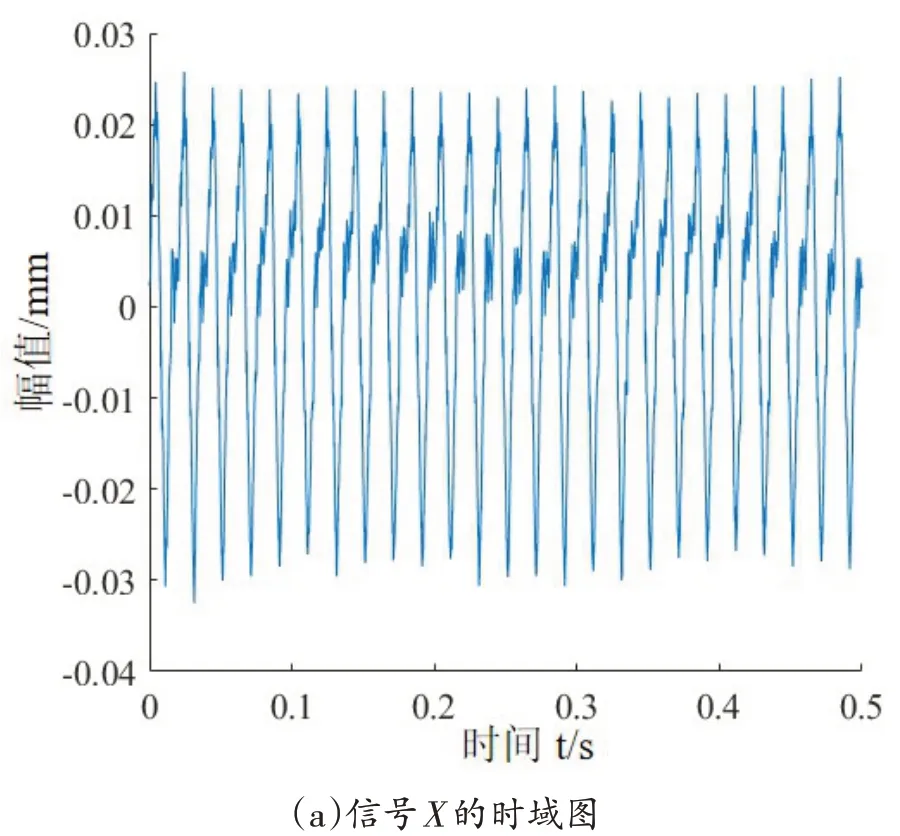
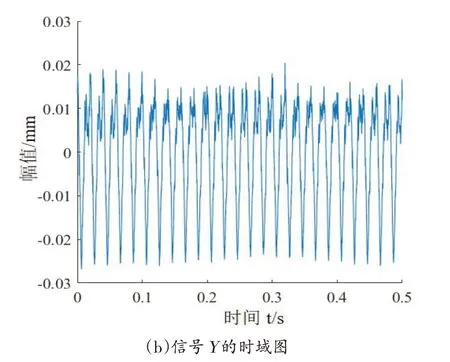
图7 信号X和Y的时域图
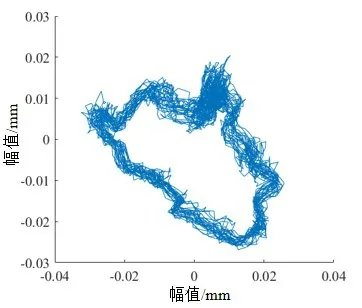
图8 原始轴心轨迹图
3 FFT-SVD轴心轨迹降噪
根据转子不对中实验采集转子的横向信号X和径向信号Y按照图1流程进行降噪,步骤如下:
(1)对采集的转子轴向信号X和径向信号Y按照式(1)构造Hankel矩阵;
(2)将矩阵按照式(2)进行SVD 降噪,如表2 所示为信号X和信号Y的奇异值(取前10个奇异值);
(3)对信号X和信号Y进行FFT变换得到如图9所示的频域图(取前500 Hz);
(4)根据频域图中主要频率个数选取奇异值个数;
(5)将确定的奇异值个数按照式(7)进行矩阵重构,得到重构信号X*和Y*;
(6)把重构后的信号X*和Y*合成轴心轨迹,完成轴心轨迹的降噪提纯;

图9 信号X和Y的频域图
表2 为信号X和信号Y前10 个奇异值的具体数据,表3为信号X和信号Y频域图中前5个幅值对应的频率数据。

表2 信号X和Y的奇异值
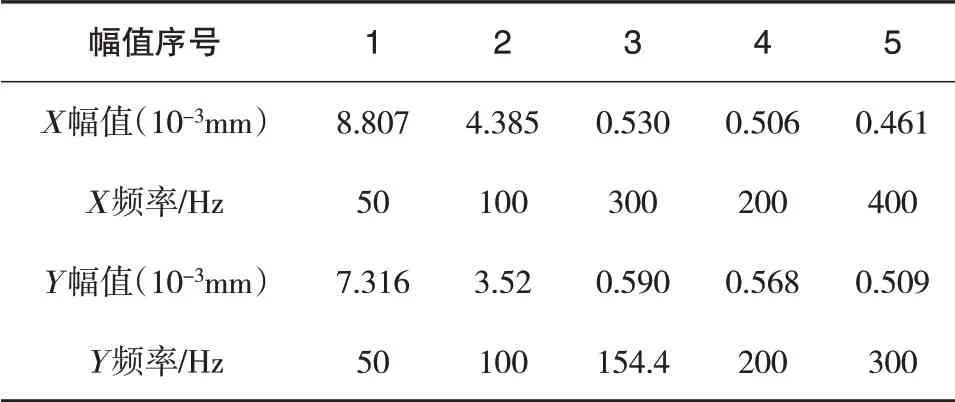
表3 信号X和Y频率幅值及对应频率
随机取表2 中信号X和信号Y第1 对奇异值(22.520,22.499)和(18.769,18.764)、第2 对奇异值(11.388,11.367)和(8.636,8.630)、信号X的第3 对奇异值(1.386,1.385)、信号Y的第5 对奇异值(1.308,1.307)来分别重构信号,经FFT变换后得到如表4所示的每对奇异值对应的频率和原始频率对比图。
实验研究发现,原始信号幅值频率和每对奇异值按照从大到小排列,每2个奇异值对应一个频率幅值,因此可以用特征频率个数选取有效奇异值来重构信号。
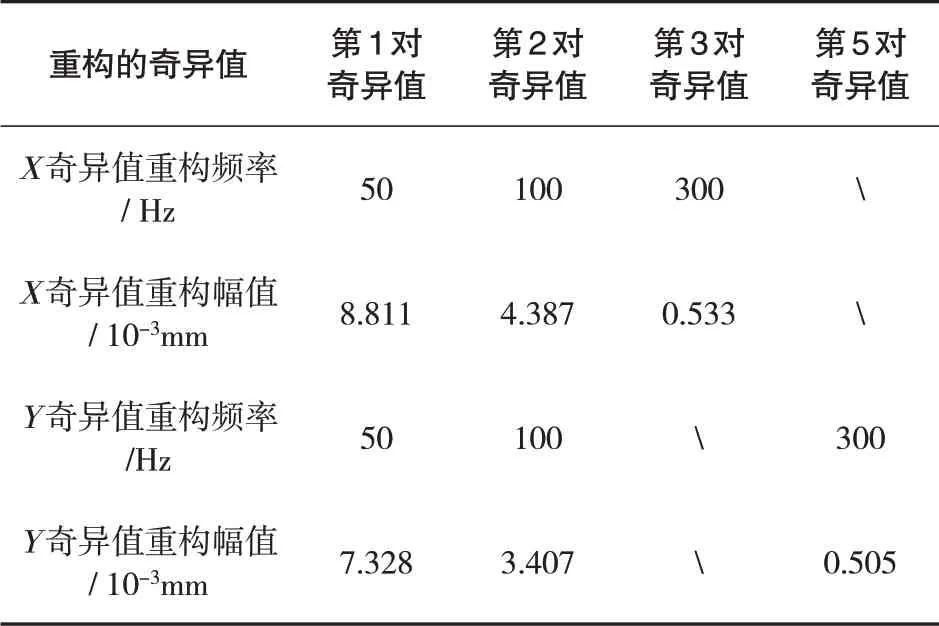
表4 奇异值重构后频率和幅值
由图9中信号X和信号Y频域图可知,特征频率主要有50 Hz 和100 Hz,分别为信号的基频和二倍频,和理论上转子发生不对中特征频率(主要是基频常伴随着二倍频)一致,根据频率和奇异值的对应关系,选取前4个奇异值按照式(7)来重构信号,则重构后的信号分别为X*和Y*如图10所示,把信号X*和Y*合成轴心轨迹,如图11为FFT-SVD算法降噪提纯后的轴心轨迹。
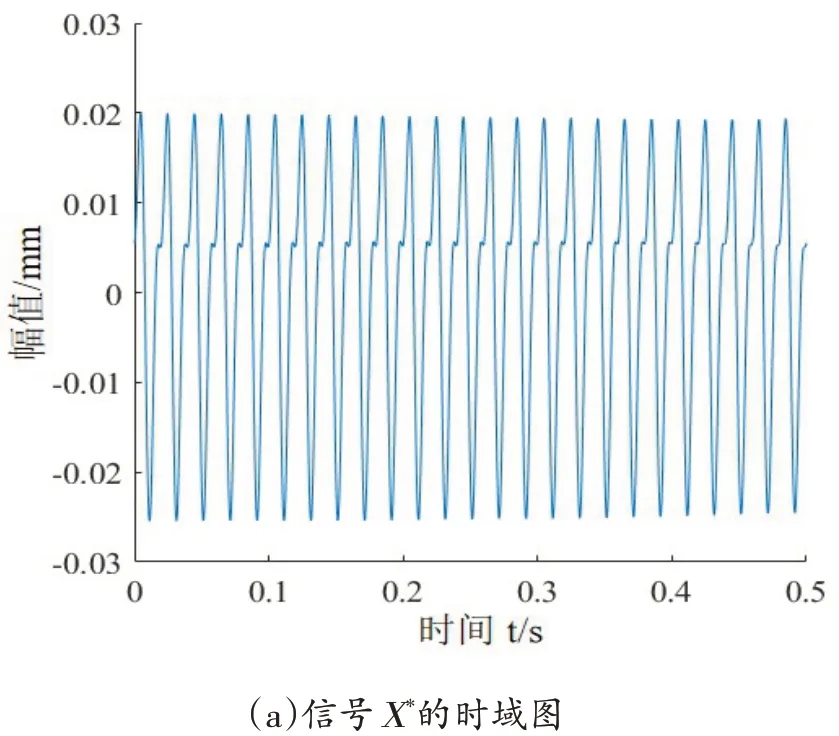
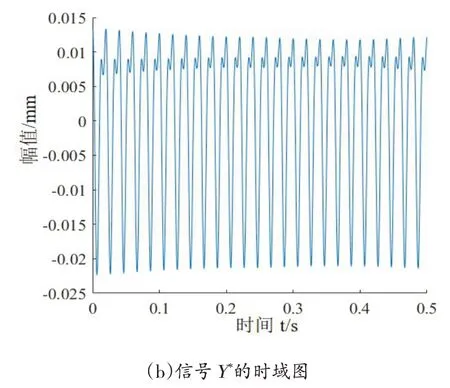
图10 信号X*和Y*的时域图
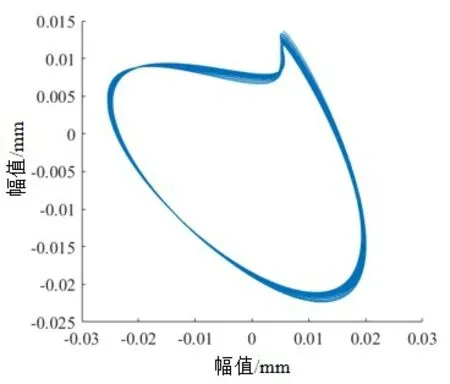
图11 FFT-SVD降噪后轴心轨迹
文献[13]表明转子系统出现不对中故障时理论轴心轨迹为香蕉形,严重为8字形。
图11 中降噪提纯后的轴心轨迹清晰光滑为香蕉形,与理论相符。因此,FFT-SVD 算法根据特征频率选取奇异值,能有效对转子轴心轨迹进行提纯,并成功检测出转子不对中故障。
4 其他算法轴心轨迹降噪
奇异值差分谱算法是通过上一个奇异值和下一个奇异值做差,按照差分谱峰值对应的序列来确定有效奇异值,再根据信号重构实现信号降噪提纯。如图12所示为信号X和Y奇异值和奇异值差分谱,图中差分谱的峰值均对应序列2,因此选取前两个奇异值进行信号重构,将重构后的信号合成轴心轨迹如图13所示。
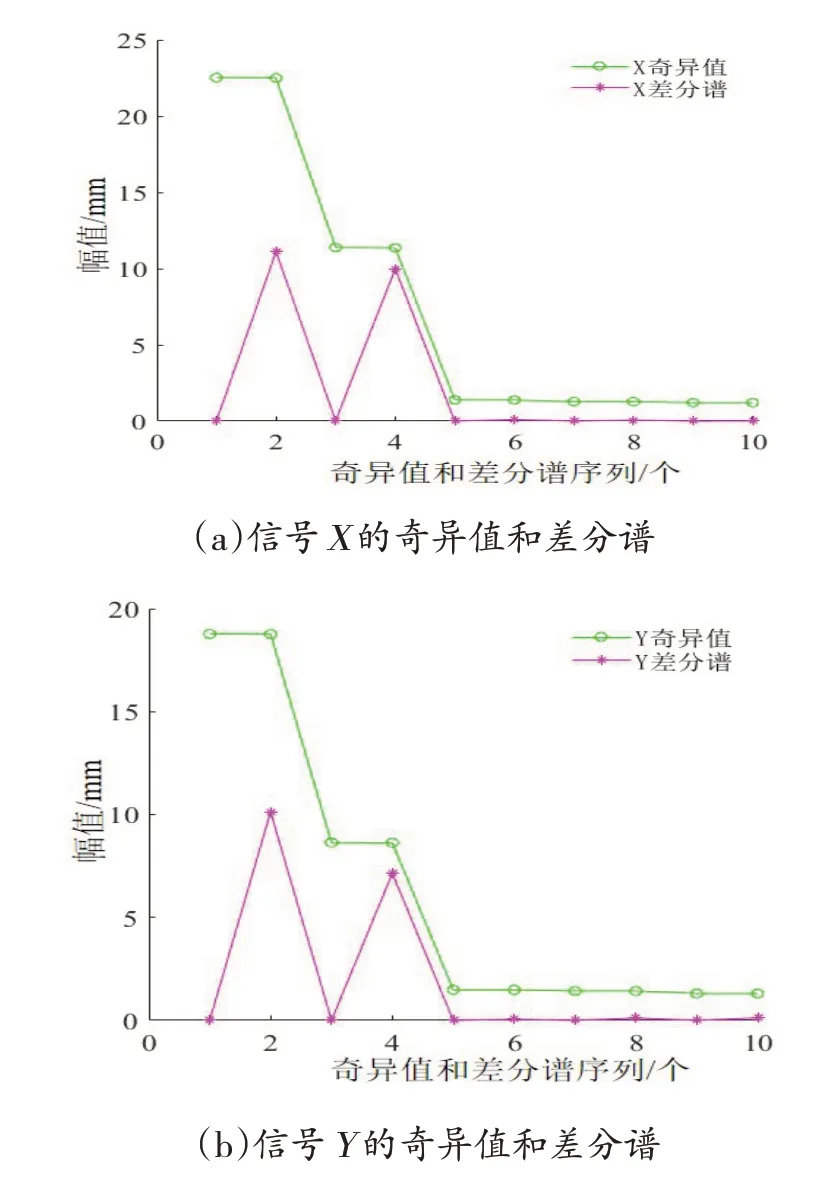
图12 信号X和Y的奇异值和差分谱

图13 奇异值差分谱降噪后轴心轨迹
按照EMD算法和小波阈值算法对信号X和信号Y进行降噪处理,将降噪后的信号合成的轴心轨迹如图14所示。
如图12 信号X和Y的奇异值差分谱所示,当差分谱的第1 个峰值和第2 个峰值相差不大时(信号X为89.8%,信号Y为70.6%),通过第1 个峰值选取奇异值重构信号会造成信号失真,合成的轴心轨迹畸形,无法通过轴心轨迹检测转子故障。
实验结果表明:和奇异值差分谱、EMD 和小波阈值算法降噪提纯相比较,FFT-SVD 算法通过特征频率选取奇异值,能有效对轴心轨迹进行降噪提纯,并成功检测出转子不对中故障。
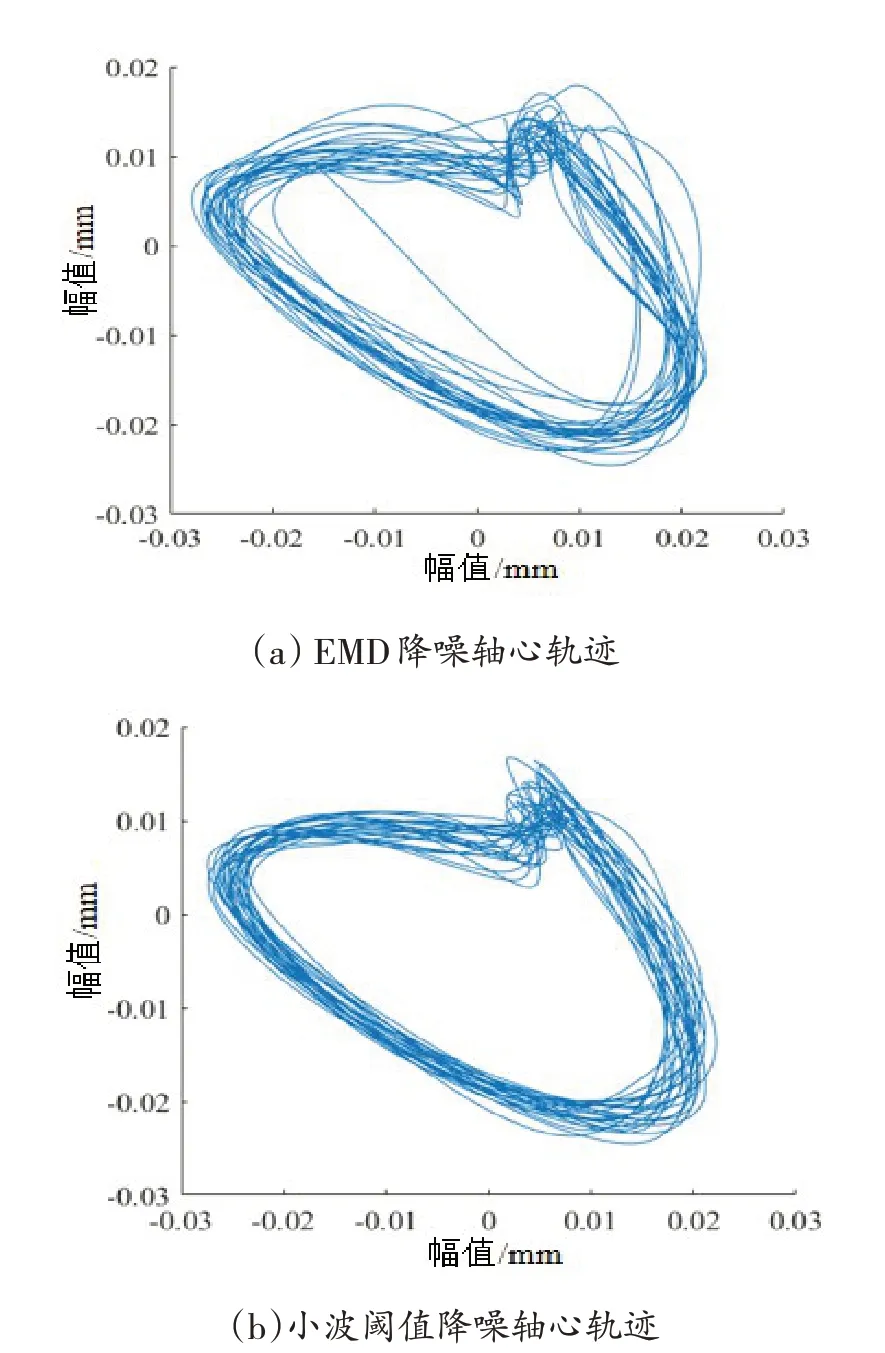
图14 EMD和小波阈值降噪后的轴心轨迹
5 结论
本文将采集的转子轴向信号X和径向信号Y进行FFT 变换和SVD 分解,发现频率和奇异值存在对应关系,因此,根据特征频率个数确定有效奇异值,进行信号重构并合成轴心轨迹完成降噪提纯,最后和奇异值差分谱、EMD 和小波阈值降噪算法相比较,得到以下结论:
(1)实验发现,信号频域图中频率和SVD分解后的奇异值存在对应关系,按照从大到小的排列顺序,每两个奇异值重构后的信号频率和原始信号频率对应。由信号X和Y频谱图中可见转子主要频率为2个(信号X和信号Y均为50 Hz,100 Hz),因此,选取前4个奇异值进行重构,将重构后的信号合成轴心轨迹。重构后的轴心轨迹清晰光滑,有效去除了干扰信号,并成功检测出转子不对中故障。
(2)使用奇异值差分谱算法对转子轴心轨迹降噪提纯发现:当差分谱中出现第二个峰值且和第一个峰值相差不大(信号X是89.8%,信号Y是70.6%)时,按照差分谱使用第一个峰值选取奇异值进行重构信号,会导致信号失真、丢失重要特征、合成的轴心轨迹畸形,很难去检测转子故障。
(3)和EMD、奇异值差分谱、小波阈值降噪算法相比较,FFT-SVD 算法对轴心轨迹的提纯最干净有效,小波阈值算法降噪次之,EMD分解算法降噪残留噪声最多。因此,本文研究算法能有效能用于转子轴心轨迹提纯,并成功检测出转子不对中故障。
