基于互质阵列的无人机载雷达空时自适应处理技术研究进展

汪小叶

（惠州学院 计算机科学与工程学院，广东 惠州 516007）

无人机载雷达是一种架设在无人飞机上的雷达传感器，通过下视工作方式采集低空或地面感兴趣运动目标信号，它可用于军事侦察与武器制导、战场监视与预警、空中交通管制、安防安保（如武警、消防、公安等政府部门应用）、高速路面巡查等，具有无人员伤亡危险、空间利用率高、自主控制能力强、任务种类多样等特点，在军事和民用领域都具有重要的应用价值。但是，无人机体积小、携带载荷能力和续航能力受限，如何实现无人机载雷达小体积、低成本、低功耗已成为人们关注的焦点。另外，机载雷达通过下视工作方式获取低空或地面感兴趣目标信息，面临的地杂波强度大，分布范围广。因此，杂波抑制是机载雷达需要解决的主要问题。

空时自适应处理（Space-Time Adaptive Processing，STAP）技术联合时域和空域二维数据，可以实现强杂波中的慢速目标检测，是机载雷达进行杂波/干扰抑制的关键技术。自1973年Brennan和Reed发表的一篇论文中提出了STAP以来［1］，雷达研究学者们开展了大量的STAP杂波抑制技术的研究工作。STAP技术的基本原理是利用参考距离单元空、时域的二维信息估计出待检测单元的杂波统计特性，并设计自适应匹配滤波器抑制杂波。这里要求利用参考距离单元估计得到的杂波统计特性与待检测距离单元的统计特性相同。但是由于实际机载雷达应用场景复杂，不同距离单元的杂波统计特性各不相同，特别是阵列模型非理想、杂波空间-多普勒频率非线性等情况下，利用参考距离单元估计的杂波统计特性很难与待检测单元的杂波统计特性匹配，因此，STAP 技术在实际应用中仍是面临着一些难点问题。目前STAP研究工作大致可分2个方面：一是针对实际环境中各类非理想因素（如杂波环境的非均匀、由阵列几何结构导致的杂波非平稳、杂波分布非高斯）的STAP 技术；二是针对降低计算复杂度的STAP快速算法设计。

近年来，随着压缩感知和稀疏恢复技术的快速发展，互质阵列作为压缩采样的新型空域实现方式，广泛应用于雷达的多维信号处理（如空间、时间维等），可以克服传统奈奎斯特采样限制的缺点，可以实现低复杂性、低成本、高频段的雷达系统需求。另一方面，稀疏分布的互质阵列具有增加自由度和增大阵列孔径的特性，可以有效解决传统机载雷达受载机平台重量和天线孔径约束的问题，从而有利于实现机载雷达的小平台、多任务的设计需求，并具有提高雷达信号处理的参数分辨性能和杂波抑制能力的潜能。因此，互质阵列STAP技术研究得到了雷达领域学者们的广泛关注，成为了当前的一个研究热点。但是，互质阵列引入机载雷达将使空时自适应处理面临许多新的问题。因此，针对互质阵列的无人机载雷达开展STAP 技术是值得进一步深入研究的方向。

1 互质阵列引入无人机载雷达的重要意义

随着电子硬件和信号处理技术的发展，无人机向体积小、成本低、功能多、续航能力强方向快速发展。由于无人机平台小，载荷重量、造价成本、工作频段、续航能力受实际应用的限制，对无人机载雷达提出了小体积、低成本、低功耗的需求。目前大部分的机载雷达阵列按照奈奎斯特采样进行配置，高频段高分辨力的雷达系统阵元数较多、系统复杂、阵列互耦严重、功耗高、成本较高。互质阵列（嵌套阵列可看作是一种特殊的互质阵列）是通过稀疏布置阵元，以一种不满足奈奎斯特采样的方式工作。例如，图1 是一种扩展互质阵列的示意图，它是由2 个均匀稀疏的线性阵列交织而成，其中子阵列1中的阵元数为2N1、阵元间距为N2d0；子阵列2 中的阵元数为为N2、阵元间距为N1d0。d0为满足奈奎斯特采样的最小阵元间距，N1,N2互为互质数，且N1＜N2。由于2个子阵列的第1个元素重合，所以扩展互质阵列的阵元数为N= 2N1+N2- 1。

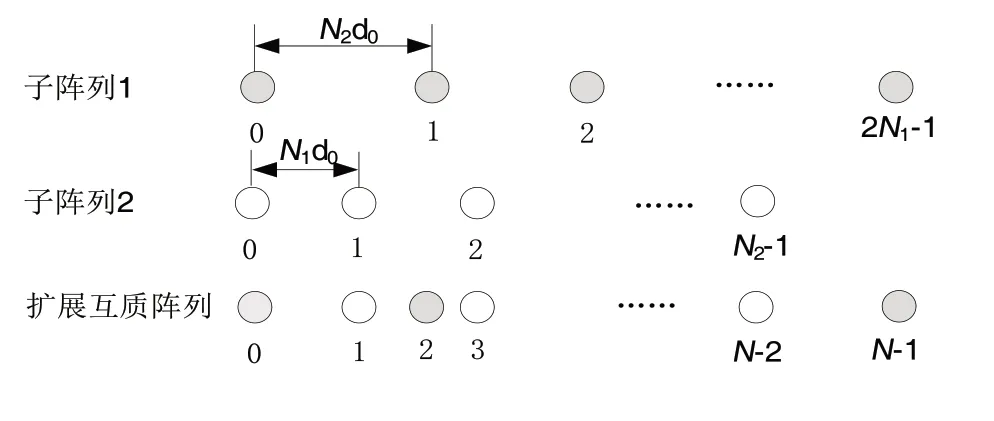
图1 扩展互质阵列示意图

令0 ≤n1＜2N1- 1，0 ≤n2＜N2- 1，定义下面差变量

那么遍历所有n1,n2的所有取值，得到的所有k的取值的集合称为差共阵，其可看作是子阵列1 和子阵列2产生的差共阵。由于N1,N2互为互质数（除了1以外没有其他公因子），差共阵中的k 的个数增多。例如，假设阵元数N= 6 的扩展互质阵列，其中N1=2,N2= 3，其变换得到的差共阵如图2所示。

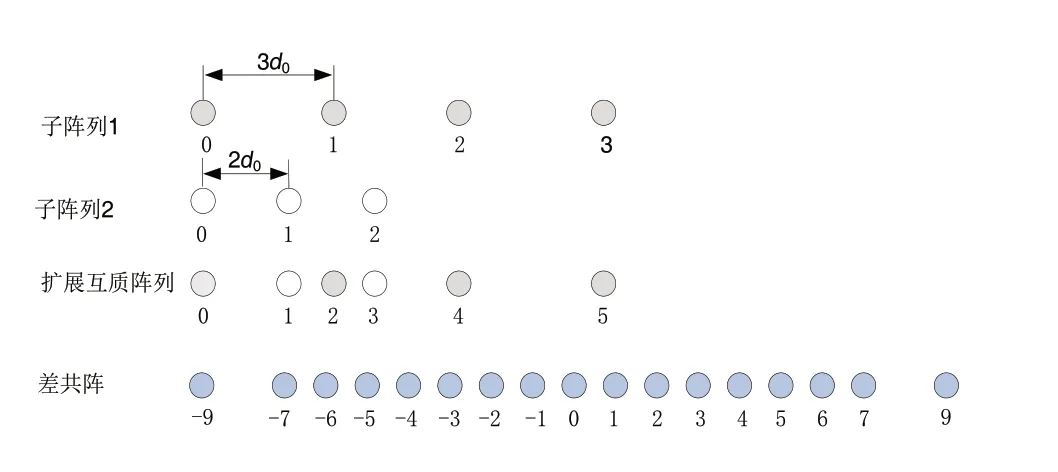
图2 N1 = 2, N2 = 3 的扩展互质阵列及差共阵示意图

由文献［1-4］可知，差共阵的物理意义即是阵列接收信号的自相关。因此具有更多自由度的差共信号可以由陈列接收信号的自相关变换得到，从而可以实现利用较少的物理阵元数等效得到更大阵列孔径的均匀阵列信号的杂波统计特性，即协方差矩阵。从而有望实现无人机载雷达小体积、低成本、低功耗的需求。由此可知，相比传统满足奈奎斯特采样的均匀阵列，互质阵列具有明显的优点：（1）采用更少物理阵列的互质阵列，通过变换可以得到与同孔径的传统均匀阵列相同数量的阵元，能够降低阵列冗余、减少接收通道数量和处理模块、降低成本和系统复杂性，从而实现雷达低成本、低功耗、小型化；（2）利用互质特性，互质阵列具有孔径扩展和阵列自由度增多的特性，从而具有显著提高杂波抑制性能的潜能；（3）对于高频段雷达半波长阵元间距小，均匀阵列可能存在安装困难，且阵元间的互耦影响较大。然而互质阵列本质上是稀疏非均匀的阵列，其阵元间距大部分大于半波长，阵元间的互耦影响减小且安装更容易。因此，将互质阵列应用于无人机载雷达，对促进雷达向小体积、低成本、低功耗和低互耦发展具有重要意义。

本文首先对互质阵列STAP 当前的主要研究情况进行综述，包括互质阵列STAP 回波信号建模、互质阵列STAP 杂波自由度分析、理想情况互质阵列STAP 技术和非理想阵列模型的稳健STAP技术等方面。然后，根据互质阵列STAP的研究现状，结合相关领域最新研究进展，对今后互质阵列STAP的研究方法进行进一步的思考和展望。

2 研究现状

2.1 互质阵列STAP回波信号建模

所考虑的机载雷达系统拟采用正侧视稀疏阵列脉冲多普勒机载雷达，如图3所示。图中直角坐标系（X，Y，Z）满足右手螺旋法则，雷达天线阵列位于（X，Z）坐标平面内，无人载机平台高度为h，以速度v沿X轴水平飞行，ψ为天线轴向方向与飞行方向的夹角，即载机偏航角。假设P为斜距为Rt的距离单元上的杂波散射体，β为散射体P相对于天线轴向的夹角，α为散射体P相对于飞行速度方向的夹角，θ为方位角，φ为俯仰角。

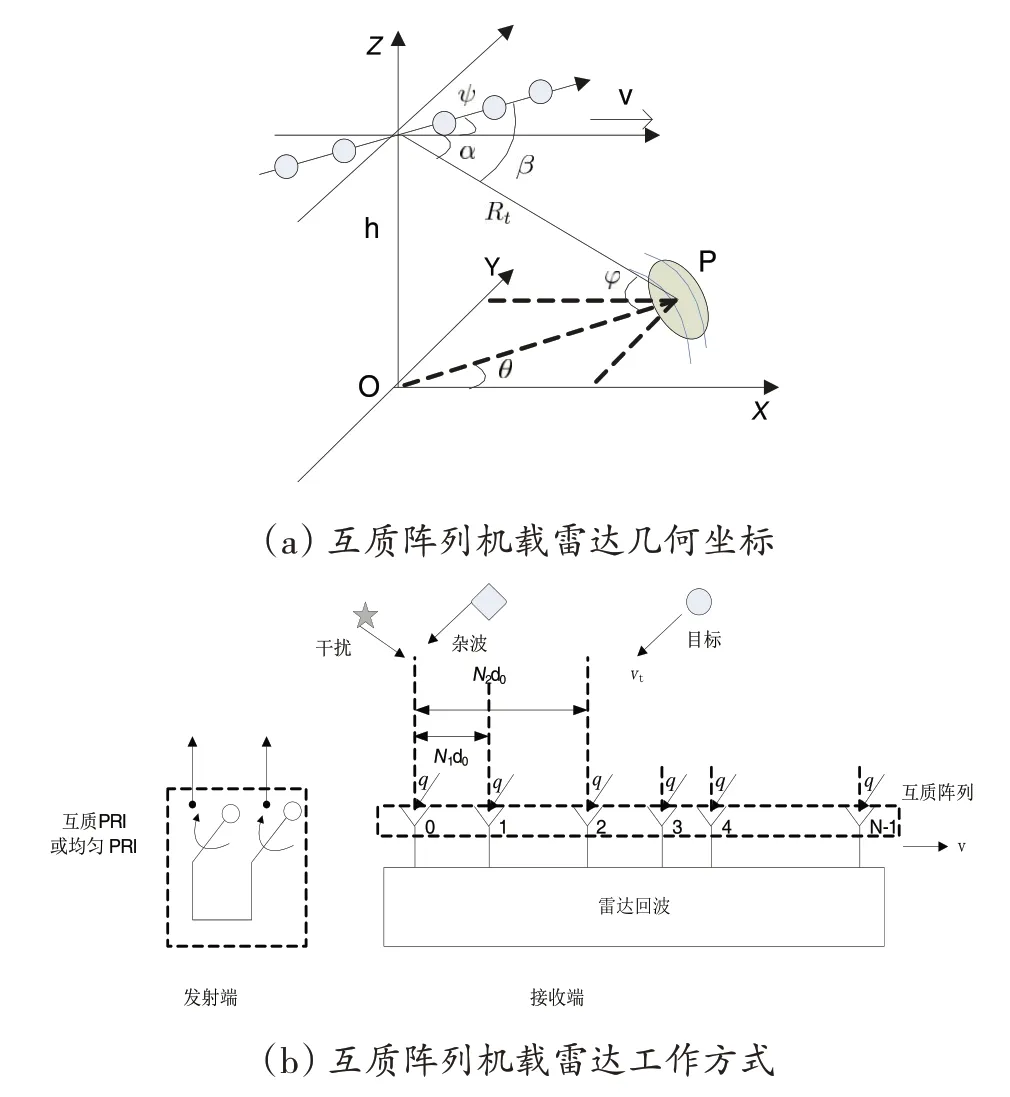
图3 互质阵列机载雷达

发射端的脉冲重复周期（Pulse repetition interval，PRI）可为互质结构或均匀结构。无人机载雷达回波一般由干扰、杂波和目标分量3 部分组成，这3 部分在接收端依次进行下变频和匹配滤波之后的信号分量称为基带信号，其基带信号可以表示为相应反射系数与导向矢量的乘积。文献［5，6］等建立了互质阵列STAP的回波信号模型，互质结构雷达基带信号模型对应的空时导向矢量v(ω,ϑ)可表述为阵列导向矢量a(ϑ)和时域导向矢量b(ω)的Kronecker积，如

其中ϑ，ω分别表示杂波的角度和多普勒频率参数。当载机非理想飞行时，其飞行方向极易偏离原定的方向，假设偏离的角度参数为Δθ，则杂波的角度频率和多普勒频率分别表示为

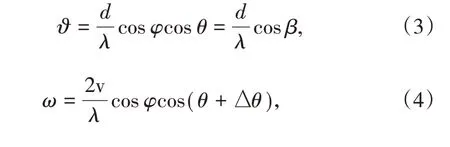
其中Δθ= 0表示载机理想飞行，Δθ≠0表示载机非理想飞行。其中cosβ= cosφcosθ。阵列导向矢量a(ϑ)和时域导向矢量b(ω)表示为

其中λ为载波波长，dn,n = 2,…,N表示相对于第1个阵元的阵元位置，以半波长为单位，tm,m = 2,…,M 表示相对于第1 个脉冲的脉冲发射时刻，以满足奈奎斯特采样定律的最小脉冲重复周期为单位。显然，阵列导向矢量a()与互质阵列阵元位置有关，时间导向矢量b(ω)与相干时间内脉冲发射时刻有关。基于已设计的互质阵列结构，导向矢量a(ϑ)和b(ω)中dn,n =2,…,N和tm,m = 2,…,M的具体值可表示出来。

最后，针对某一距离单元，雷达观测得到的回波表示为

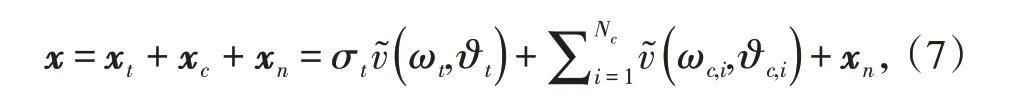
其中，xt=( ωt,ϑt)表示目标分量，σt表示目标信号反射系数，ωt,ϑt分别表示目标的多普勒频率和空域频率为杂波分量，σc,i表示第i个杂波块的反射系数，Nc为某个距离单元内的杂波块总数表示可能存在载机非理想飞行情况下的多普勒频率为ω 和空域频率为ϑ 的空时导向矢量，xn为噪声分量。对于杂波，针对均匀地面背景（如草地、沙滩、沙漠、水面、天空等）以及非均匀地面背景（如城市、树林、水陆交界等），采用网格剖分的方法计算杂波回波；对于目标，针对典型运动目标（如车辆、行人、无人机、船舶等）采用统计方法计算其回波；对于接收机热噪声，假设服从高斯分布。

2.2 互质阵列STAP杂波自由度分析

Wang 等［7］利用杂波自由度（即杂波秩）依赖于机载雷达的阵列结构的特性，从稀疏阵列下的杂波回波信号模型出发，结合孔径带宽积理论估计出杂波秩。例如，假定互质阵列可以划分为K个满足奈奎斯特采样的均匀子阵，每个子阵的孔径为Lk，接收信号带宽为B，则利用孔径带宽积估计的杂波秩表示为

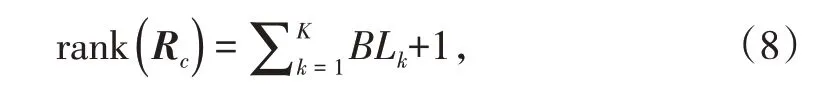
其中，rank(·)表示求括号内的矩阵的秩。最后，利用系统自由度和杂波秩的关系即可分析杂波抑制的理论最优性能。

针对实际雷达的平台速度和偏航角存在测量误差时，文献［8］利用先验知识约束误差范围，推导了一种扩展的互质阵列杂波秩估计方法。其结果表明了该方法在先验知识存在误差情况下，可获得较好的性能，且该方法可适用于正侧视和非侧视2种情况。刘等［5］从物理互质阵列和物理互质脉冲结构出发，提出了多种固定自由度模型，表明互质阵列和互质脉冲可用于解决无人机平台易变形、载荷有限的问题。

2.3 互质阵列STAP技术

由于互质阵列STAP 的空时维数相较于传统均匀阵列减少，且互质变换得到的差共阵样本是一维相干信号，如何有效估计协方差矩阵是一个难点问题。现有互质阵列STAP研究成果主要集中在以下3类方法：第一类是基于空时平滑的方法；第二类是基于稀疏恢复的方法；第三类是基于Toeplitz矩阵的等效样本空洞填充方法。

（1）基于空时平滑的方法：文献［9］首次提出了互质阵列互质脉冲重复周期的STAP方法，该方法利用互质结构特性推导了自由度增多和阵列孔径增大的虚拟空时快拍，利用空时平滑方法得到满秩协方差矩阵，改善了目标角度-多普勒参数的估计精度。文献［10］在嵌套阵列结构（可以看作是一种特定的互质阵列）的基础上，提出了一种阵列和脉冲联合设计的嵌套结构，并提出了两种基于虚拟等效信号的杂波抑制方法：一种是利用物理互质阵列接收的回波信号估计出的杂波协方差矩阵虚拟变换，并通过空时平滑得到自由度增加的满秩协方差矩阵；一种是基于等效虚拟的样本估计出杂波的角度-多普勒参数，然后设计自由度增加的滤波器。但是文献［10］未提及如何利用物理互质阵列接收的回波信息估计杂波协方差矩阵和角度-多普勒信号。不同于上述空时二维的互质结构，文献［11］考虑了互质脉冲重复间距（PRI）的STAP 方法，利用物理互质PRI 等效变换得到更多脉冲的虚拟等效脉冲，并基于空时平滑方法设计滤波器实现杂波抑制。Wang X等人［12］提出了一种空时二维互质采样的空时自适应处理方法。文献［7］进一步分析了空时二维互质采样的杂波秩及有限快拍下虚拟快拍估计误差分布。文献［13］提出了一种基于嵌套阵列嵌套脉冲重复周期的STAP方法，该方法利用空时平滑方法估计虚拟等效协方差矩阵，在一定样本数量下实现了机载雷达杂波的有效抑制。考虑到上述方法需要的样本数较多的问题，文献［14］提出了一种降维空时平滑空时自适应处理方法，相比全维互质空时采样STAP方法有更快的收敛性。注意空时平滑只能利用虚拟等效信号的连续采样部分的数据，然而虚拟等效信号中包含有非连续采样的数据。文献［15］考虑到典型嵌套阵列的最小阵元间距仍为半波长可能存在阵元间互耦效应的问题，提出了一种针对超嵌套阵列的基于空时平滑的STAP 方法，该方法利用嵌套阵列的较大的阵元间距减少了阵元间的互耦效应，同时仍可获得好的杂波抑制性能。文献［16］采用双载频空时互质采样结构等效出更多的自由度和更大的阵列孔径设计虚拟域STAP方法，相比单载频互质阵列STAP获得了更优的杂波抑制性能。

（2）基于稀疏恢复的方法：为充分利用全部的虚拟空时信号的数据，文献［17］提出了一种基于稀疏的互质空时采样的STAP 方法，该方法利用杂波的稀疏性，建立了杂波在虚拟域上的稀疏表征模型，然后利用最小绝对收缩选择算法（Least Absolute Shrinkage and Selection Operator，LASSO）高精度地重构杂波谱，最后基于估计的杂波谱计算协方差矩阵并推导STAP 权矢量。仿真表明在一定强度的杂噪比场景下，相比上述基于空时平滑的方法有更好的杂波抑制性能和收敛性。文献［8］针对上述基于稀疏的互质空时采样STAP方法计算复杂度大的问题，提出了一种基于知识的两阶降维稳健稀疏STAP 方法，降低了算法计算复杂度，提升了小样本下杂波抑制性能。

（3）基于低秩矩阵恢复的方法：由于空时平滑方法仅适用于均匀奈奎斯特采样条件，因此基于空时平滑的方法只能利用等效虚拟信号的连续样本信号，而基于稀疏恢复的方法虽不受均匀奈奎斯特条件的限制，可以利用全部等效虚拟信号。由于等效虚拟信号存在空洞，因此上述2 种方法并没有完全利用互质虚拟的特性。文献［18］利用杂波协方差矩阵的低秩特性，利用迹最小化的优化方法，借助CVX 工具箱，估计出物理互质阵列接收信号的协方差矩阵；然后借助互质特性等效出更多的虚拟样本用于设计滤波器，从而充分利用互质带来自由度增多和杂波抑制性能提高的优势。

上述STAP方法考虑的是理想的稀疏阵列结构，针对非理想的稀疏阵列结构，近几年公开报道了一些稀疏阵列模型失配（阵元位置误差、幅相误差、以及互耦）的研究成果［19-23］。例如，Lu R等人建立了阵列模型误差（如幅相误差、阵元位置误差、互耦）下的虚拟等效信号模型，证明了3 种阵列模型失配下虚拟等效阵列仍具有扩展自由度的特性，并提出了稀疏贝叶斯联合估计DOA和误差系数的方法［19，20］，仿真验证了该方法相比无校正的方法对阵列误差有更好的稳健性。Wang M等人从理论上分析了阵列位置误差对共阵MUSIC方法影响，推导了共阵MUSIC在阵列存在位置误差时仍具有增加自由度的特性［21］。文献［22］从理论上分析了虚拟等效阵列DOA估计的克拉美罗界，进一步从理论上分析了阵列误差对虚拟等效阵列DOA 估计的影响。另外，文献［24］提出了一种基于稀疏的幅相误差和杂波功率谱联合估计的杂波抑制方法，有效提高了阵列幅相误差下的杂波抑制性能。

3 讨论与展望

基于互质阵列的STAP 技术利用较少的物理阵元可以获得同孔径的均匀阵列的杂波抑制潜能，对于实现无人机载雷达的低成本、低功耗、高频段具有极大的潜力。但是该技术的研究尚处于理论探索阶段，特别是在实际复杂的应用场景以及小型化的无人机平台下，存在一系列关键科学问题值得进一步的研究。基于互质阵列的无人机载雷达STAP技术的特点是：一方面，无人机工作频段高，形状各异；且平台小、轻，载机平台的结构极易受环境影响发生变形；飞行速度易受风速影响发生偏航。另一方面，互质阵列的稀疏采样造成杂波秩增加，空时采样数据减少，且等效虚拟信号是一个存在空洞的单快拍信号。因此，针对上述特点，基于互质阵列的无人机载雷达STAP 技术未来值得重点解决和关注的研究方向总结为以下几个方面：

（1）考虑无人机非理想飞行下的稳健STAP 方法。目前，互质阵列STAP技术多是针对理想的载机平台下的STAP 方法。较少考虑无人机在恶劣天气等影响造成的载机偏航、及载机变形引起的阵列变形等情况下的稳健性问题。因此，针对无人机非理想飞行下的稳健STAP是一个值得关注的方向。

（2）考虑阵列模型失配的稳健STAP方法。现有文献中互质阵列的虚拟等效信号依赖协方差矩阵的块Toeplitz结构特性，当存在阵列非理想时，如幅相误差、阵元位置误差等，阵列非理想破坏了协方差矩阵的这种Toeplitz结构特性，从而造成互质阵列的虚拟等效信号阵列模型失配。目前，阵列模型失配下的一维阵列信号处理研究已有部分成果，研究发现了阵列模型失配下的互质阵列仍具有增加自由度和改善参数分辨力的优势。但是互质阵列STAP技术尚处于起步阶段，鲜有考虑阵列模型失配下的稳健STAP技术。因此，阵列模型失配下的互质阵列STAP技术有待进一步研究。

（3）考虑高斯和非高斯混合背景下的STAP 方法。目前文献中的互质阵列STAP 技术仅考虑了高斯环境下的STAP 方法。但是实际低空空域的无人机载雷达系统工作环境复杂，当雷达系统遇到雷电、采样通道故障等特殊情况时，雷达接收数据可能兼具有突变尖峰、长拖尾、相关等非高斯特性，这种噪声结构使得抑制杂波的任务更加困难。另一方面，杂波幅度的起伏变化，独立同分布的训练样本数据较少。由于非高斯分布类型的数据，其二阶统计量不存在，而传统的互质阵列杂波抑制STAP 方法都是基于雷达阵列接收数据的二阶统计量进行设计的，高斯、高斯非高斯混合背景下如何有效估计虚拟等效信号。这些都是未来值得进一步研究的方向。

（4）考虑小样本下的STAP 方法。现在互质阵列STAP假定了大量的独立同分布样本数，鲜有考虑小样本下的STAP方法。但是无人机工作场景复杂，一方面很难获得大量的独立同分布样本数；另一方面，无人机载雷达回波中可能包含强地杂波和强干扰。为了解决上述问题，未来可以结合传统的样本挑选法、深度学习方法、先验知识辅助等研究小样本下的STAP方法。

4 结语

本文综述了基于互质阵列的无人机载雷达STAP的研究进展，介绍了互质阵列引入无人机载雷达的重要意义；概述了当前互质阵列STAP技术及非理想阵列模型下的稳健STAP技术；讨论了目前基于互质阵列的STAP技术走向实用化面临的一些问题，提出了互质阵列STAP技术在互质阵列结构的优化设计、特定互质阵列结构下的杂波谱分布的分析、以及高斯非高斯环境的非理想阵列模型的稳健STAP 技术等方面开展进一步的研究。