1981—2020年安徽省不同重现期最大风速和极大风速时空变化特征

李丽，王业斌，鲁俊，王晓东，吴萍，陶寅

(1. 安徽省气象灾害防御技术中心，安徽 合肥 230031；2. 安徽省农业气象中心，安徽 合肥 230031；3. 国家气候中心，北京 100081)

1 引 言

根据《风电场风能资源评估方法》(GB/T 18710—2002)规范[1]定义，最大风速是指10 min 平均风速的最大值，极大风速为瞬时风速的最大值。大风作为一种灾害性天气，会对农业、畜牧业、大气环境、交通、电信、建筑等领域造成很大的危害。

随着高耸建筑物、大型桥梁等大型工程项目的增多，由于高楼建筑之间的“狭管效应”，导致风速比空旷地区强度更大，常常造成严重的城市风灾[2]。近年来，风速观测资料不断丰富，国内外对于大风灾害的研究越来越多。主要集中在大风的时空变化[2-6]、大风灾害风险评估区划[7-9]、风速预报[10-11]和大风预警[12]以及大风灾情分布特征等方面。国内风速极值重现期的研究区域主要集中在沿海等热带气旋较为多发的地区[13-17]，多以利用极值Ⅰ型[18]和广义极值[19]分布等方法实现重现期估算为主。上述研究多关注平均风速、最大风速，而对瞬时极大风速研究较少。但实际上，由于城市有热岛效应，城市瞬时极大风速局地性强，危险性大，是城市面临的主要气象灾害之一[2]。大多数建构筑物在发生大风灾害时，同期气象站的最大风速并未超过线路的设计风速，依然发生建筑物振动事件[20]或工程事故。目前，我国建构筑物设计风速以最大风速计算重现期作为主要设计依据，但由于最大风速统计时距过长的局限性，难以准确反映大风灾害的实际情况，往往会造成计算值偏小，不能反映瞬间风速造成灾害的实际情况[21]。同时，对比国际及国外建筑荷载设计标准，如ISO 4354：2009《风力对建筑物的作用》[22]规定了用于设计建筑物、塔架、烟囱、桥梁和其他结构及其部件和附件的风荷载特征值的计算方法，其中给出了两种设计风荷载的计算方法，一种是基于峰值风速，另一种基于平均风速；澳大利亚/新西兰标准AS/NZS 1170.2：2011《结构设计作用与风的作用》[23]在计算风力作用时规定使用的现场风速则是为3 s阵风风速。综上所述，极大风速重现期的计算对于建构筑物抵御风灾的能力、提高工程运行的可靠性、加强城市防灾减灾工作具有重要意义。

由于目前极大风速的观测资料年限较短，较短的观测资料可能会造成各风速重现期估算强度偏小[24]。且短序列时长的观测资料不能满足诸多工程50年或者更长年限的重现期估算。本文首先利用安徽省2006—2020年逐日最大风速和极大风速观测资料，计算逐日阵风系数，完成1981—2020年极大风速的长时间序列资料构建，并将该极大风速数据与现有的不完整数据进行比对，以验证构建方法的科学合理性。其次对历年最大风速和极大风速的时空分布进行分析，估算安徽省不同重现期的最大风速和极大风速，并对极大风速序列延长前后重现期估算情况进行了对比，以期为安徽省大型工程建设气象设计参数的确定、城市建设布局规划、气候变化监测评估等提供参考和科学依据。

2 资料和方法

2.1 数据资料

本文所用的资料：安徽省内国家基本气象站及常规气象站(78个气象站)逐日最大风速(1981—2020年)与极大风速(有资料年—2020年)资料。数据来自全国综合气象信息共享平台(CIMISS)，均通过台站-省级-国家级三级质量控制。

2.2 数据情况

根据国家级气象观测站名录，安徽省目前在用国家级气象观测基本站和一般站共78 个。自1971 年陆续开始有自计10 min 平均最大风速观测，自1981年起，各气象站的最大风速数据基本有了完整的观测记录；自1993 年起安徽省陆续有极大风速的观测，至2006 年实现全省站点的极大风速的连续观测。根据《气候可行性论证规范抗风参数计算》(QX/T 436—2018)[25]“应收集参证气象站30 年以上历年最大风速数据，以及与专用气象站同期观测的逐日最大10 min 平均风速、逐时风速和风向数据，有效数据完整率应大于或等于90%”的要求，本文剔除有效数据完整率[1]低于90%的12 个台站，剩余的66 个气象站最大风速有效数据完整率均在97.76%以上，其中61个台站均超过99%。

其次根据《地面标准气候值统计方法》(GB/T 34412—2017)[26]数据质量控制要求，查询各站历史沿革，对该61个站年最大风速序列进行Weibull分布均一性检验[27]，剔除其中迁站导致观测数据突变、存在非均一点的10 个台站，最终选取其中51个最大风速序列均一、有效数据完整率超过99%的国家级气象观测基本站和一般站。图1 为研究区域和本文选取的51个气象站分布图。

2.3 研究方法

2.3.1 长时间极大风速序列资料构建

采用阵风系数法对1981—2005年间无观测数据的极大风速进行估算。因为各站的地面粗糙度各不一致，按照《公路桥梁抗风设计规范》[28]地面粗糙度分类进行计算不具针对性，同时得出的结果并不严谨。

本文根据史军等[3]、纪玲玲等[5]的研究成果，首先将2006—2020年安徽省各站逐日极大风速与当日最大风速相除，得到逐日阵风系数。

逐日阵风系数的计算按照式(1)计算：

式中：G 为阵风系数(无量纲数)，Vmax为逐日极大风速(单位：m/s)，V为当日最大风速(单位：m/s)。

统计发现，逐日最大风速大于11 m/s的样本较少，所以将各站逐日最大风速按[1，2)，[2，3)，……，≥11 m/s区间分别划分11个等级，对应同站同步的逐日阵风系数进行计算，不同区间内阵风系数较稳定，阵风系数才有意义。最终计算得到51 个气象站各区间阵风系数的平均值变化曲线以及各区间阵风系数的标准差(图2)，可见在风速较小时阵风系数的均值和波动幅度较大，且随着风速的增大而减小，这与文献[29-30]对阵风系数的研究结论一致。当风速达到6 m/s以上时，阵风系数趋于稳定；同时，不同区间内阵风系数的标准差为0.07～0.13，离散程度较小，区间内阵风系数较稳定。

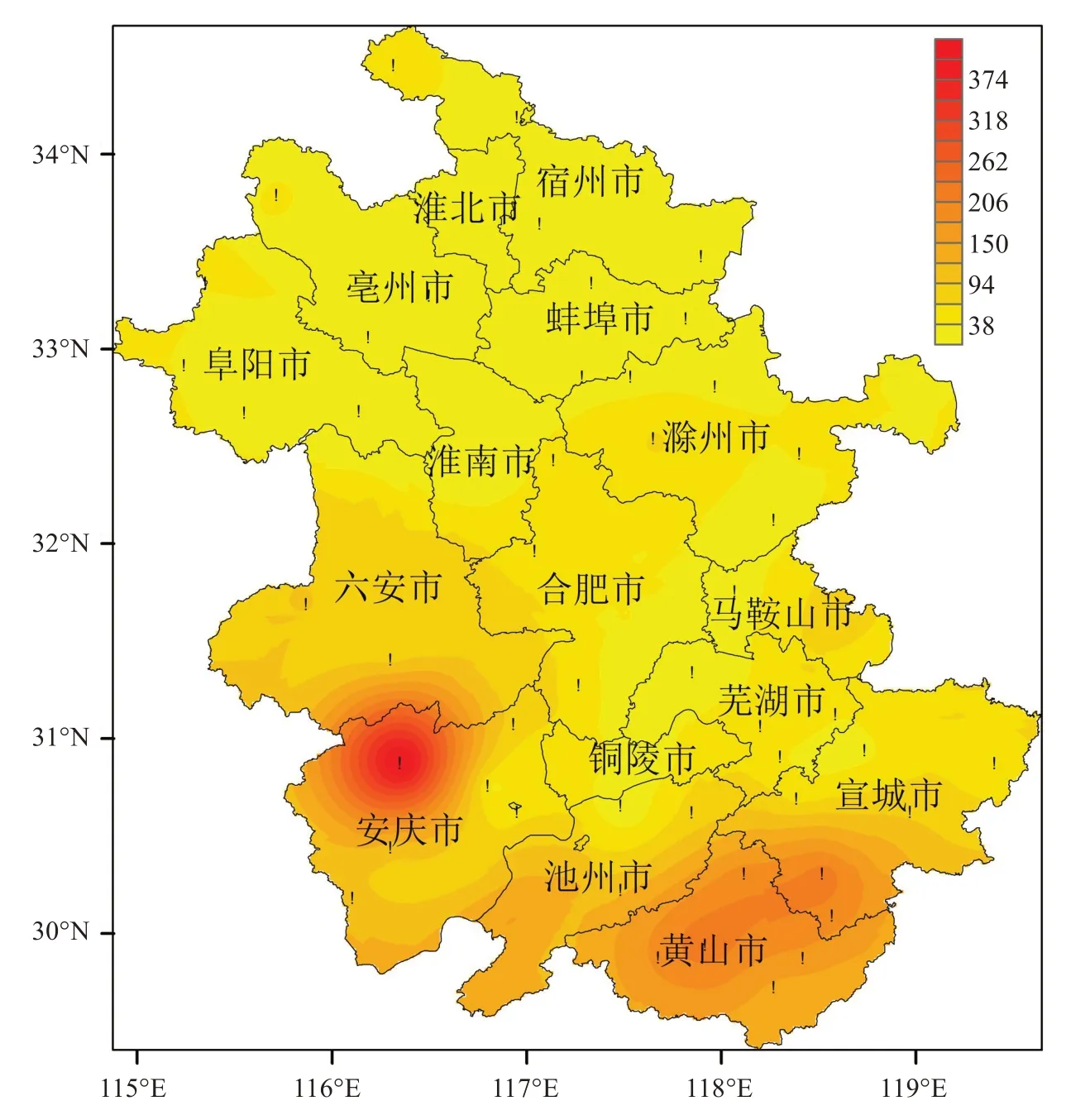
图1 各气象站点分布及海拔高度(单位：m)

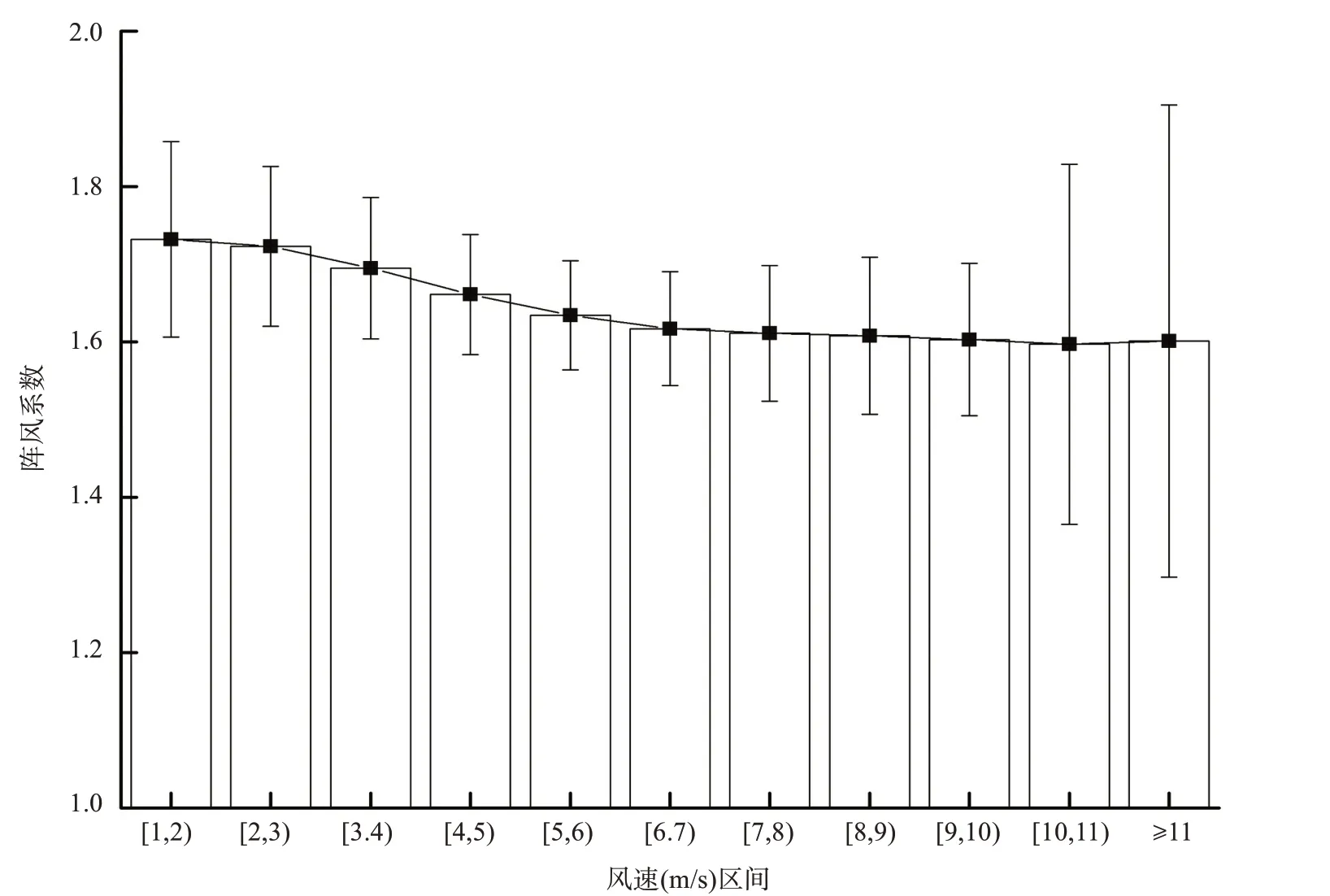
图2 1981—2020年安徽省各风速区间的阵风系数及其标准差

根据各区间等级的阵风系数，对安徽省1981—2005 年间缺少的极大风速进行资料构建，利用逐日最大风速乘以该区间等级的平均阵风系数，合并各站原有极大风速观测数据，从而构建出1981—2020年极大风速的长时间序列资料。

由于各气象站建设以及观测起始时间不一致，安徽省有部分台站极大风速观测较早，将通过阵风系数法构建的极大风速与现有观测数据(共289 个样本)进行相关性分析，相关系数达0.725，并在0.01 水平(双侧)上显著相关。说明通过最大风速利用阵风系数法构建的极大风速数据可信，可用做极大风速重现期的估算。

2.3.2 插值方法

Kriging插值是一种常见而简便的空间插值方法，依据区域变化采样点收集的数据，提供未知采样点区域变化的最优线性、无偏估计[31]。其计算公式如式(2)：

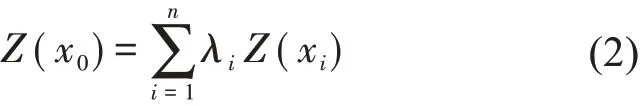
式中：Z 为气象站点的估计值，x0为空间中任意待插值位置，xi为站点位置，n 为插值点总个数；λi为插值过程中各气象站点权重系数，即= 1，使得被估计的参数和估计量的数学期望值相等，并使其方差要小于任意的线性组合方差。

本文利用ArcMap10.2的Kriging插值方法，对选取的51 个气象站风速的气候变化趋势以及30年、50年重现期估算值进行了空间插值。

2.3.3 极值估算

采用极值Ⅰ型[25]概率分布函数计算不同重现期的最大风速和极大风速。极值Ⅰ型的概率分布函数F(x)如式(3)：

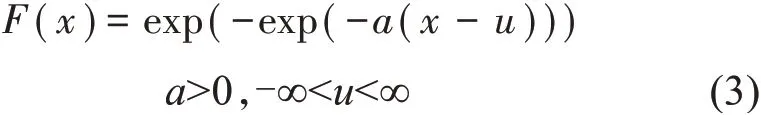
式中：a 为尺度参数，u 为位置参数，两者均为无量纲数。

2.3.4 检验方法

本文采用柯尔莫哥洛夫-斯米诺夫检验法[32]对风速序列是否服从极值Ⅰ型概率分布进行检验。其统计量如式(4)：

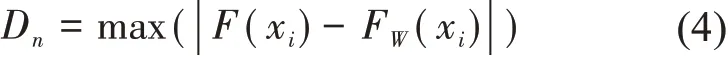
式中：Dn为统计量，表示在所有格点上，假设理论分布与经验概率分布之差的最大值；F(xi)为概率分布函数在xi处的概率值；FW(xi)为有序序列在xi处的经验概率值。

对于不同的显著性水平α 和n，可查表获得检验临界值λα,n。若Dn＜λα,n，则接受原假设，认为样本符合假设理论分布；否则，则为拒绝原假设。

3 结果与分析

3.1 最大风速与极大风速空间变化特征

1981—2020 年，安徽省历年平均最大风速为12.38 m/s，各站为9.13～17.61 m/s，桐城气象站最大，石台气象站最小（图3）。从最大风速数值上看，淮北平原、大别山区和皖南低矮山区为风速低值区，沿江西部处于相对大值区。大体表现为山区的局地性差异比淮北平原和江淮之间的丘陵地区风速空间差异更为明显。整体风速空间分布与安徽地形有着密切的关系[6]。

图4a、4b 分别为2006—2020 年实测和序列延长的1981—2020年安徽省历年平均极大风速空间分布，可见其空间分布形势与最大风速的空间分布类似。就2006—2020 年极大风速实测数据而言，历年平均极大风速强度为18.88 m/s，各站为16.25～23.00 m/s。皖南低矮山区的极大风速值较低，历年平均极大风速在18.18 m/s以下，沿江西部及江淮之间中部的极大风速大值区达20.30 m/s以上。其中，极大风速历年平均最大值出现在太湖站，为23.00 m/s，而最小值出现在屯溪站，为16.25 m/s。对比图4a、4b 可以发现序列延长的1981—2020年各站历年平均极大风速强度明显大于2006—2020 年实测的各站强度。1981—2020年历年平均极大风速强度为20.55 m/s，各站在17.51～26.74 m/s，空间分布差异较大。

3.2 不同重现期下最大风速和极大风速估算强度空间分布

按照柯尔莫哥洛夫-斯米诺夫检验法，分别建立51 个气象站点1981—2020 年最大风速、年极大风速的极值Ⅰ型概率分布函数，对其拟合适度进行检验。取信度0.95，查表获得该检验中的临界值为1.35。通过计算，发现检验值均小于检验阈值1.35，因此本文所用风速样本序列服从极值Ⅰ型概率分布。可利用该分布进行安徽省30 年和50 年重现期最大风速和极大风速的估算。

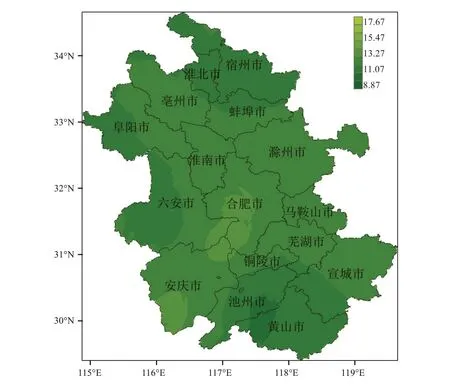
图3 1981—2020年安徽省历年平均最大风速空间分布(单位：m/s)

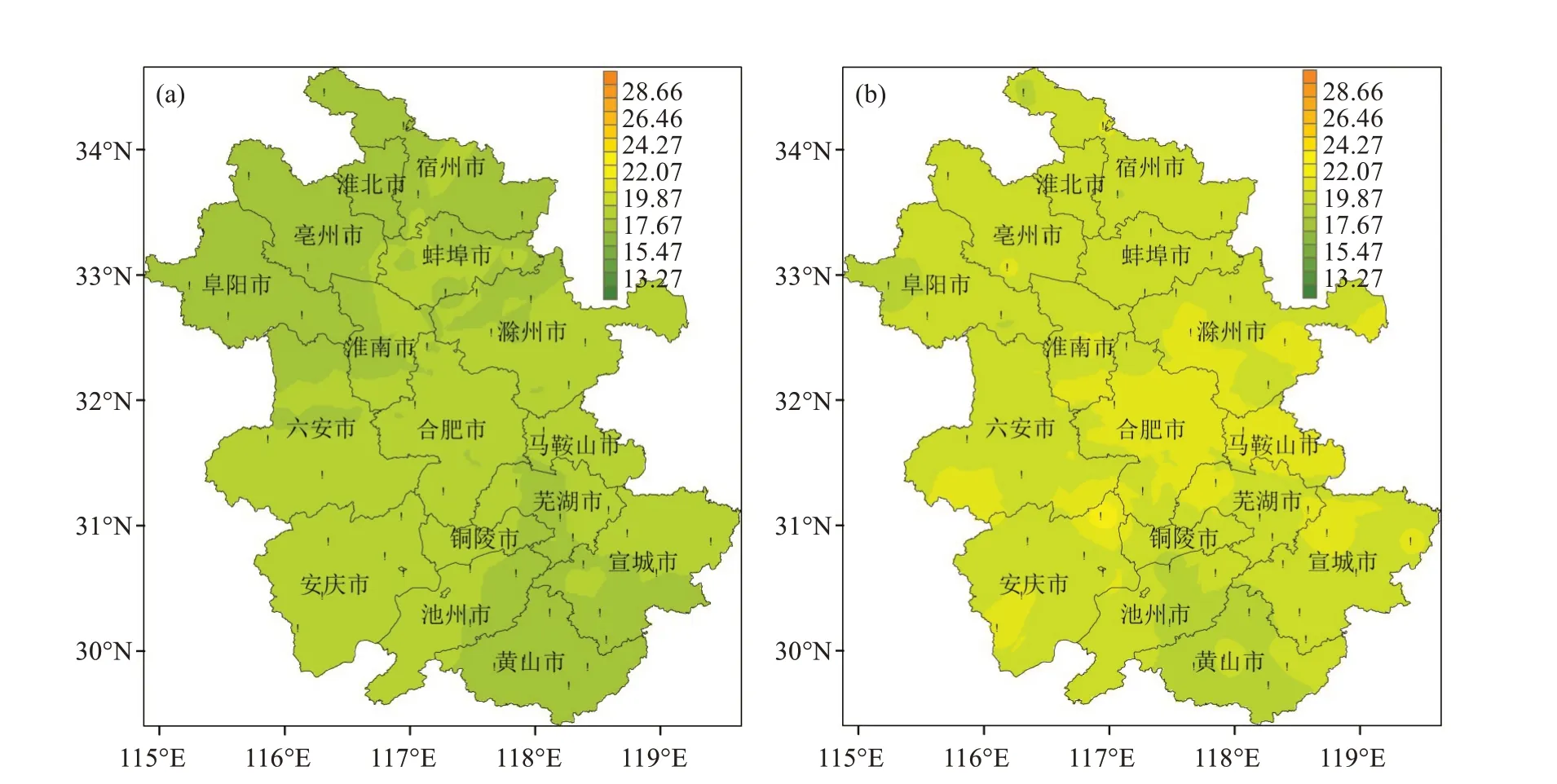
图4 安徽省2006—2020年(a)、1981—2020年(b)平均极大风速空间分布(单位：m/s)

3.2.1 不同重现期下最大风速估算强度空间分布

图5 给 出1981—2020 年 安徽省30 年和50 年重现期最大风速空间分布。安徽省各地30年重现期 最 大 风 速 强 度 为12.09～27.23 m/s，50 年 为12.64～29.01 m/s，均是石台站最小，桐城站最大。从空间分布上看，安庆、宣城地区以及北部的利辛站和霍邱站为重现期估算高值区，30 年重现期最大风速超过21.3 m/s，50 年重现期最大风速则在22.9 m/s以上。

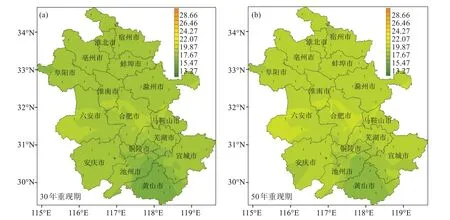
图5 基于1981—2020年观测数据估算安徽省30年(a)和50年(b)重现期最大风速空间分布(单位：m/s)

3.2.2 不同重现期下极大风速估算强度空间分布

图6 和图7 分别为利用不同年限长度资料估算30 年和50 年重现期的极大风速。由2006—2020 年极大风速数据估算的30 年和50 年极大风速重现期空间分布与历年最大风速、极大风速以及1981—2020年极大风速重现期空间分布上存在一定的差异，且估算的重现期值较长时间序列估算的重现期值偏低。分析原因，一方面由于城市化进程导致气象站周边粗糙度增加等多种影响，中国地面风速总体呈减弱趋势[33]导致基于现有实际观测的极大风速资料估算的重现期值明显低于序列延长的重现期估算值；另一方面由于工程建设项目抗风参数中重现期推算应基于30年以上的风观测资料[25]，短期的观测资料会降低估算结果的可靠性。

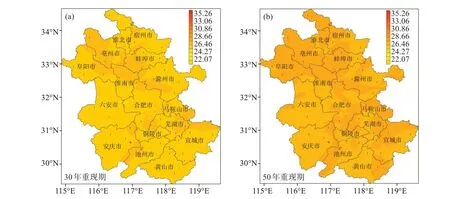
图6 基于2006—2020年观测数据估算安徽省30年(a)和50年(b)重现期极大风速空间分布(单位：m/s)

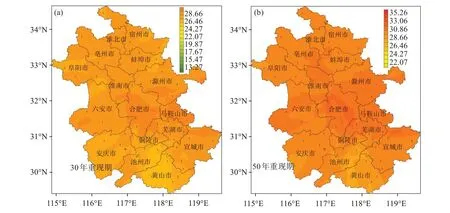
图7 基于1981—2020年观测数据估算安徽省30年(a)和50年(b)重现期极大风速空间分布(单位：m/s)

基于最大风速、阵风系数以及现有极大风速逐日观测资料构建的1981—2020 年极大风速，利用极值Ⅰ型分布进行30 年和50 年重现期极大风速的估算，结果表明，极大风速重现期值和观测的极大风速空间分布类似。30 年重现期极大风速为23.51～39.56 m/s，50 年为24.58～41.93 m/s，均为池州站最小，桐城站最大。

4 结 论

本文根据相关规范分别从质量控制级别、有效数据完整率、是否均一等方面考虑，选取安徽省51 个气象站1981—2020 年逐日10 min 最大风速和2006—2020 年逐日最大风速资料，基于最大风速资料应用阵风系数法构建1981—2005年极大风速，得到1981—2020 年极大风速的长时间序列数据；对风速资料进行拟合适度检验，估算安徽省不同重现期最大风速和极大风速的时间变化以及空间分布，并对极大风速序列延长前后重现期估算情况进行了对比。

(1) 利用2006—2020 年安徽省51 个气象站逐日极大风速与当日最大风速计算逐日阵风系数，针对不同风速区间通过阵风系数法计算了1981—2005 年极大风速，构建了1981—2020 年长时间序列的极大风速，通过相关性分析以及风速重现期估算，证明利用该方法构建的极大风速数据可信，可为因缺少长时间序列的极大风速观测而无法进行50年或者更长重现期估算提供参考。

(2) 1981—2020 年安徽省历年最大风速强度为12.38 m/s，极大风速强度为20.55 m/s。其空间分布基本一致，均为皖南低矮山区的风速值较低，沿江西部及江淮之间中部处于相对大值区。经过序列延长的1981—2020年各站历年平均极大风速强度明显大于2006—2020 年实测的各站强度，与安徽省大部风速普遍呈现显著减少趋势结论一致[34]，同时表明短期的观测资料会降低估算结果的可靠性。

(3) 安徽省各地30 年重现期最大风速强度为12.09～27.23 m/s，50 年为12.64～29.01 m/s，均是石台站最小，桐城站最大。基于1981—2020 年极大风速估算的30 年重现期的极大风速为23.51～39.56 m/s，50 年为24.58～41.93 m/s，均为池州站最小，桐城站最大。

(4) 对比序列延长前后的极大风速重现期估算结果。由2006—2020 年极大风速数据估算的30 年和50 年极大风速重现期空间分布与历年最大风速、极大风速以及1981—2020 年极大风速重现期空间分布上存在一定的差异，且估算的重现期值较长时间序列估算的重现期值偏低，表明短期的观测资料会降低估算结果的可靠性。