不同幅值作用下振动台斜坡动力响应模拟分析

邹 玉

(中铁十八局集团有限公司，天津 300350)

0 引 言

伴随着我国“一带一路”的发展和青藏铁路的建设，大型交通基础设施的建设越来越多.基础设施建设沿线途中会经过较多地质地貌，面临众多地质灾害[1].其中滑坡对于工程建设中的影响不可忽视，已经引起了国内相关学者的研究与讨论[2].为了进一步了解在地震作用下斜坡的动力响应特性和失稳破坏机理，为斜坡的地震稳定性分析提供可靠依据，通过数值模拟对振动台斜坡试验进行前期分析.首先对不同地震动幅值作用下的斜坡动力响应特征和变化规律进行研究，斜坡的动力响应主要包括位移、速度和加速度，其中斜坡的加速度响应及其分布规律是研究斜坡在地震作用下动力响应的主要研究内容[3].

本文选取某典型滑坡，通过Midas GTX建立概化斜坡振动台模型，对斜坡进行多种工况数值模拟，研究斜坡模型在不同幅值作用下的动力响应规律[4]，以此对未来在该地区进行工程建设提供一些参考和依据，对工程的安全性有更好的保障.

1 工程背景及岩性

1.1 工程背景

滑坡高差约为700m，滑坡后缘高程约为3300m，前缘坡趾高程约为2600m.岩层倾向坡内，倾角在55°～70°，倾向N30°E.滑坡后缘最高点至左岸冲击区最高点总长度约为180m，左右边界最大宽度约为730m，斜坡剖面图如图1所示[5].

图1 斜坡剖面图

1.2 滑坡岩性

滑坡为反倾斜坡的倾倒破坏，滑坡区主要出露石英砂岩和片岩，岩体结构面发育.坡内岩性的主要为石英砂岩，成层性较好，表面风化强烈.堆积体主要成分为石英砂岩夹少量片岩，滑坡区域内岩性变化不大[6].

2 数值模拟计算模型

2.1 建立计算模型

通过振动台模型箱尺寸、斜坡剖面图及相关条件，确定了振动台斜坡模型的尺寸相似比CL=1000，密度相似比Cρ=1，重力加速度相似比Cg=1.根据郑颖人等[7]模型建立原则和相似理论，建立了坡高为0.95m，坡长为4.5m，坡宽为1.5m的斜坡振动台模型.通过相似比确定的数值模拟中斜坡的物理力学参数如表1.

表1 基本力学参数表

2.2 边界条件及监测点

在数值模拟中，对半无限模型斜坡进行动力输入时，需进一步考虑边界条件.为减小反射波对输入波的影响，减小能量发散问题，在模型斜坡四周中设置为二维自由场边界，模型底部及自由场下部设置为固定边界，边界底部设置B1、B2两个监测点.材料本构模型采用理想弹塑性模型中的Mohr-Coulomb模型.沿坡面从低到高设置A1、A2、A3、A4和A5，沿坡内垂直方向设置A6、A7、A8和A9，斜坡上共设置9处监测点.斜坡动力分析数值模型监测点布设及边界条件示意图，如图2所示.

图2 监测点位置示意图 图3 输入地震波与输出点a、b的加速度时程曲线

2.3 检验边界条件

合理的边界条件是数值模拟准确的前提.为检验边界条件的设置是否正确，通过在边界底部设置多个监测点，将监测点B1、B2记录的地震波时程曲线与输入的典型汶川波(051BXZ，31.0°N 103.4°E，基岩)进行对比分析.结果如图3所示，记录与输入时程曲线吻合程度较高[7]，证明了输入地震动和施加的边界条件的正确性、合理性.

2.4 工况设计

为研究在不同动力输入参数下斜坡的动力响应特性，数值模拟中输入的地震波为正弦波，地震波输入方向为X向(水平方向)，输入不同幅值为0.1g、0.2g、0.3g和0.4g，频率分别为10hz、15hz、20hz和25hz，持时均为10s，如表2所示.

表2 各工况地震动参数

3 不同幅值下斜坡的动力响应规律

本节主要考虑在不同幅值下，斜坡的动力响应特性，在数值模拟中通过改变单一变量—幅值，对模型斜坡施加动力作用，从斜坡的位移、速度和加速度的情况展开对比分析[8].

3.1 位移响应

斜坡在不同幅值的正弦波作用下，斜坡上各监测点的最大位移值也不同，如表3所示.从坡表监测点来看，坡脚A1处的位移值最小，随着高程的增加，位移值逐渐变大，位于坡顶A5处的位移值最大；对比坡内和坡表监测点位移值，可以发现位于坡表的监测点发生的位移略大于坡内；在同一频率下，随着幅值的增大，位移也相应增长，即幅值与斜坡位移值为正相关；随着频率的增大，位移出现先增大后减小的趋势.

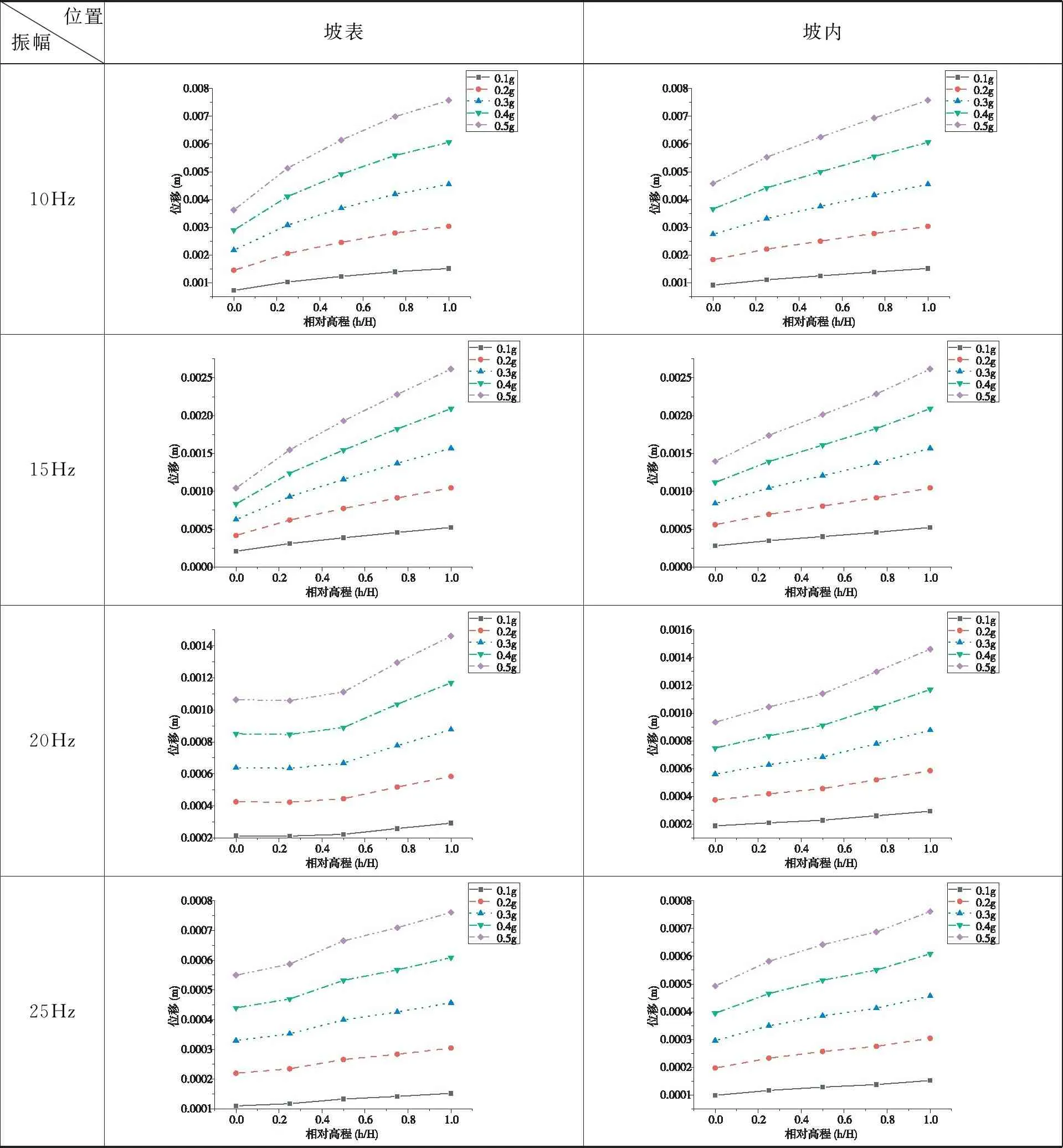
表3 不同幅值下位移

3.2 速度响应

斜坡在不同幅值的正弦波作用下，斜坡上各监测点的速度值也不同，如表4所示.从坡表监测点来看，坡脚A1处的速度值最小，随着高程的增加，速度值逐渐变大，位于坡顶A5处的位移值最大；对比坡内和坡表监测点位移值，可以发现位于坡表的监测点发生的位移略高于坡内；在同一频率下，随着幅值的增大，速度也相应增长，即幅值与斜坡速度值为正相关；在同一幅值下，随着频率的增大，位移出现减小的趋势.

表4 不同幅值下速度

3.3 加速度响应

斜坡在不同幅值的正弦波作用下，斜坡上各监测点的最大加速度值也不同，如表5所示.从坡表监测点来看，坡脚A1处的加速度值最小，随着高程的增加，加速度值逐渐变大，位于坡顶A5处的加位移值最大；在同一频率下，随着幅值的增大，加速度也相应增长，即幅值与斜坡速度值为正相关.在相对高程为1/2处，加速度变化趋势发生变化；在不同频率下，加速度最大值沿高程增加的程度是不一样的，并非是保持某一速率稳定增大.频率低时，斜坡的加速度响应越大，即当输入波频率与斜坡的自振频率接近时，放大效应越明显；反之放大效应越弱.

表5 不同幅值下加速度最大值图

4 结 语

本节主要是研究基于相似理论构建了斜坡振动台数值模拟计算模型，研究在不同幅值输入下对斜坡动力响应的影响，并得出以下结论：

(1)在模型斜坡四周中设置为二维自由场边界，模型底部及自由场下部设置为固定边界，通过检验输入地震波的时程曲线和边界监测点的时程曲线，输入和输出加速度时程曲线较吻合，即在底部施加的边界条件是合理的.

(2)斜坡在不同幅值的正弦波作用下，斜坡上各监测点的最大位移值、速度值也不同.从坡表监测点来看，坡脚A1处的值最小，坡顶A5处的值最大，随着高程的增加，位移、速度值逐渐变大；坡表发生的位移略大于坡内.

(3)斜坡在不同幅值的正弦波作用下，斜坡上各监测点的最大加速度值也不同.随着高程的增加，加速度值逐渐变大，位于坡顶A5处的加位移值最大，具有明显的高程效应和坡表效应.在同一频率下，随着幅值的增大，加速度也相应增长.在相对高程为1/2处，加速度变化趋势发生变化.