飞行器爆炸螺栓分离冲击环境散布分析

王玉玺，王 娟，康 骁，李 营

(1.北京理工大学先进结构技术研究院，北京 100081；2.北京电子工程总体研究所，北京 100854)

0 引言

分离技术作为航空航天技术和武器装备研发中必不可少的关键技术越来越受到重视。其中，火工分离技术以其元件少、结构简单、可靠性高、快速性好、同步性俱佳等优点在分离技术中占有主导地位。爆炸螺栓分离装置是一种目前应用广泛且相对成熟的点式火工分离装置，在航天器的分离中具有较多应用场景[1]。爆炸螺栓是利用腔内所装炸药爆炸产生的拉伸、剪切力学效应，使指定的部位断裂来完成其解锁功能。爆炸螺栓在分离机构中的安装比较简单，通过拧紧螺母或螺栓体即可将两个目标结构连为一体。爆炸螺栓在分离过程中，会出现高频、高峰值的应力波，因此会对航天器的结构或重要设备产生强作用的瞬态冲击载荷[2]。

为使火工分离技术得到广泛的应用，很多学者针对火工分离技术进行了深入细致的研究，对分离过程开展了深入的了解。王军评等[3]、汤林等[4]研究了爆炸螺栓解锁过程中冲击载荷和产生机制，发现爆炸螺栓解锁过程分为爆炸和撞击两种冲击响应，并且分析了两种载荷所占比例。侯传涛等[5]、杨帆等[6]研究了爆炸螺栓的承载能力，常英珂等[7]针对疲劳寿命的研究方法展开论证，这些研究为爆炸螺栓在航天器或导弹上的应用提供了参考依据。王鹏等[8]对爆炸分离的冲击信号进行了有效性的分析及校正，为复杂序贯试验过程中非平稳冲击情形下的关键结构状态监测及分析提供一种解决思路及方法。此外，在爆炸螺栓的设计过程中，越来越多的学者采用数值仿真的办法进行研究，提升设计的准确性[9-13]。

上述研究针对爆炸螺栓的解锁和设计过程进行了研究，但是尚缺乏针对爆炸螺栓解锁后其对飞行器结构产生的冲击响应的散布范围的研究。在飞行器设计过程中，需要针对飞行器上关键设备的防护等级，研究分离过程对飞行器结构和设备在不同频率下的响应范围，来完成对不同位置、不同等级的结构或设备的防护设计。本文采用Coupled Eulerian Lagrangian(CEL)算法，通过Abaqus有限元软件进行针对飞行器爆炸分离过程的仿真分析，研究爆炸螺栓的炸药药量和断裂端面尺寸对飞行器关键位置冲击响应散布范围的影响。

1 计算分析

1.1 计算方法

为了准确模拟爆炸螺栓分离装置在爆炸载荷作用下，产生的高温高压气体推动推杆运动，在剪切力的作用下，将薄弱处剪切掉，实现分离的过程，采用CEL方法对爆炸分离过程进行仿真计算。

在数值仿真模拟流固耦合及大变形问题时，可以将欧拉单元和拉格朗日单元耦合以获得两种算法的优点，即耦合的欧拉-拉格朗日算法(CEL算法)。在这种方法中，欧拉材料可以在拉格朗日单元上施加压力边界条件，从而引起结构的位移，拉格朗日界面可以以任意方式穿过固定在空间中的欧拉网格。反过来，拉格朗日界面为欧拉物质流提供速度边界条件，而欧拉物质不能穿透拉格朗日单元。

对于爆炸螺栓解锁过程的研究中，建立欧拉域以模拟含能材料在爆炸螺栓内部的作用过程，在数值模拟中爆炸螺栓及推杆采用拉格朗日网格进行划分并计算，空气、含能炸药采用欧拉网格进行划分并计算。计算过程中建立欧拉域，用以模拟含能炸药的爆炸环境，在欧拉域中选取指定位置的网格为含能炸药，设置起爆时间后模拟含能炸药在空腔内爆炸时的能量传递情况。爆炸螺栓、推杆及含能炸药位置如图1所示。

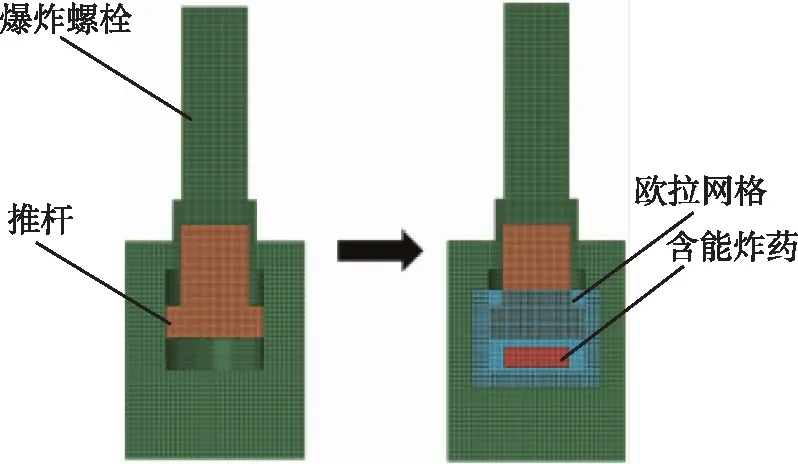
图1 爆炸螺栓及含能炸药仿真模型

为模拟炸药的爆炸螺栓腔内的爆炸过程，在仿真过程中定义含能炸药的状态方程，以模拟爆炸过程中炸药产生气体的比容与压强之间的关系。本文采用JWL状态方程来模拟含能炸药的轰爆能力，JWL状态方程的表达式为

(1)

式中，A,B,R1,R2,ω为炸药固有参数，γ为相对体积，E为比内能。

仿真计算过程中，针对爆炸螺栓受到其内部炸药爆炸产生的冲击波，使得断裂位置产生的应力大于材料的屈服强度而产生塑性变形，完成螺栓解锁过程。而Johnson-Cook本构模型主要用于高应变率、大应变以及高温下金属材料的失效过程计算，对应爆炸螺栓在爆炸分离阶段的失效过程，因此采用爆炸螺栓材料Johnson-Cook本构模型进行仿真计算。Johnson-Cook本构模型的表达式为

(2)

1.2 计算工况

1.2.1 冲击响应谱

采用冲击响应谱(Shock Response Spectrum, SRS)来描述不同条件下的冲击环境。冲击响应谱是指将冲击载荷施加到一系列线性、单自由度弹簧质量系统时，各单自由度系统的最大响应值作为对应于系统固有频率的函数而绘制的曲线，航天工程中的设计规范和实验规范都是以冲击响应谱为参数给出的。

加速度的测点位置可以根据不同分离装置结构形式进行设置，在得到各点加速的时程曲线之后，采用描述航天器爆炸冲击环境推荐的参数设置，即放大系数=10，频率间隔取1/12倍频程，采样率100 K[14]。冲击响应谱分析频率范围为100～5 000 Hz。对关键测点位置的加速度时域曲线经过频谱转换后得到冲击响应谱。

1.2.2 计算方法验证工况

研究中建立单个爆炸螺栓在钢板上解锁的实验模型，与实际爆炸螺栓在实验板上分离过程获得的数据作对比，以验证计算方法的准确性。验证模型的结构参数依据实际实验模型的加工图纸进行确定，仿真模型的结构参数与实际实验过程中各零部件的结构参数保持一致，即仿真模型与实际实验情况相符合。在欧拉域中含能炸药所处位置为爆炸螺栓实际解锁过程中安放位置，根据实际爆炸所需药量，设置仿真模型欧拉域中含能炸药网格所占体积，保证在仿真模型中药量与实际实验过程一致。依据实际实验条件，设置模型的载荷与边界条件。即在仿真过程中，模型和参数选择和边界条件均与实际情况保持一致。

验证模型及爆炸螺栓有限元网格模型如图2所示，整个模型在钢板上按距离爆炸位置的远近设置两个测点。模型为轴对称结构，采用1/4仿真模型。包括实验钢板、爆炸螺栓、异形螺母、爆炸螺栓回收罩和回收罩缓冲物。爆炸螺栓与异形螺母连接固定，回收罩内缓冲物包括橡胶和铝制蜂窝缓冲层。实验钢板尺寸为0.4 m×0.1 m×0.015 m。钢板网格尺寸为3 mm，回收罩和内部缓冲物网格尺寸为2 mm，异形螺母网格尺寸为1 mm。爆炸螺栓网格模型如图3所示，断裂位置网格进行加密处理，爆炸螺栓断裂位置网格尺寸为0.3 mm，其他位置网格尺寸为0.5 mm。整个模型在截面处建立对称边界条件，爆炸螺栓与异形螺母接触位置采用TIE约束，其他结构采用通用约束，限制图2所示固定位置结构的自由度，起到固定实验钢板的作用，整个模型受重力，重力加速度g=9.8 m/s2。

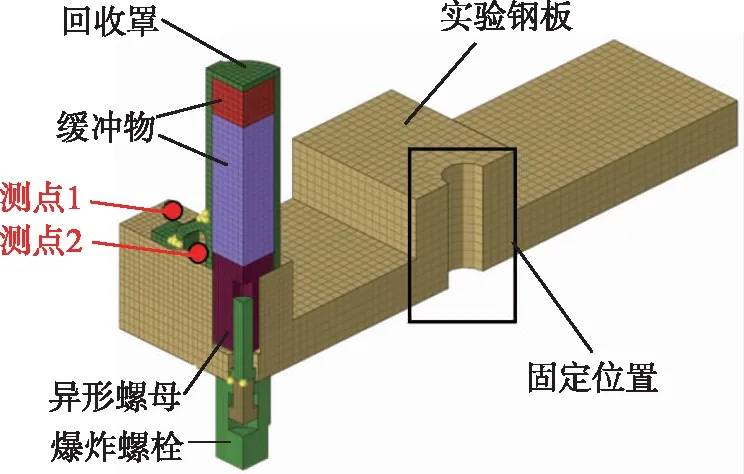
图2 有限元验证模型

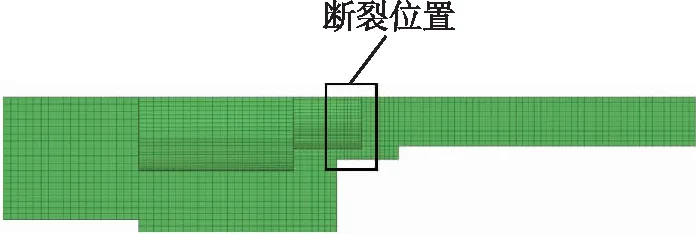
图3 爆炸螺栓网格模型

在仿真模拟中，依据实际实验中的测点位置，提取测点1和测点2位置的加速度进行频域分析，将仿真与实际实验过程中同一测点位置的冲击响应谱作对比，以验证仿真方法的准确性。其中，对于准确性验证，依据冲击响应谱通用容差标准进行确定。关于冲击响应谱的容差范围，美军标中规定在0～3 000 Hz,容差带范围为±6 dB，0～3 000 Hz以上容差带范围为+9/-6 dB,并要求有50%的正偏差[14]。仿真与实际实验结果的冲击响应谱对比如图4所示，包括实验和仿真结果的冲击响应谱曲线以及实验曲线±6 dB包络范围。采用欧拉-拉格朗日算法的有限元模型分离结果的响应谱曲线位于所要求的实验值±6 dB范围内，依据上述冲击响应谱的容差验证标准，证明了在模拟爆炸螺栓分离过程采用欧拉-拉格朗日算法的准确性。

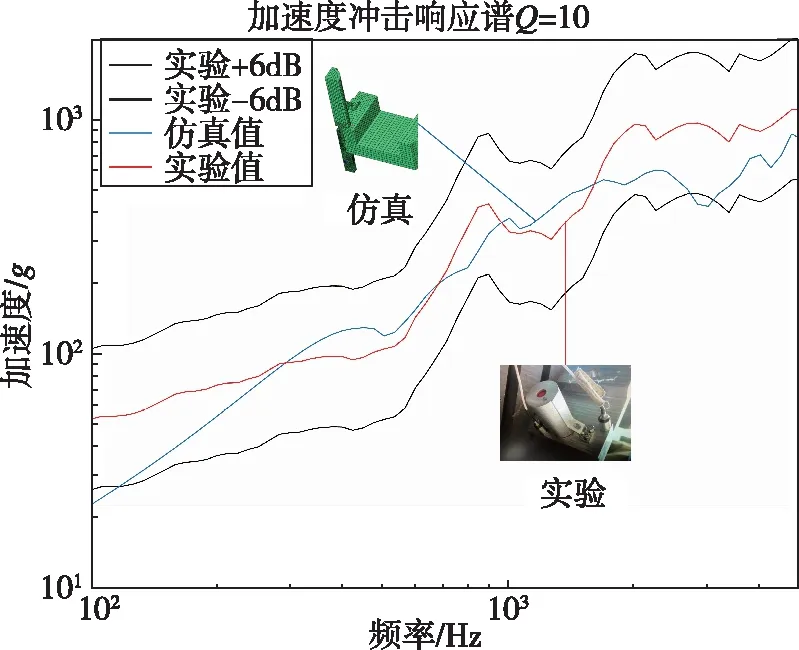
(a)测点1实验值与仿真值对比

1.2.3 有限元模型

在飞行器爆炸分离仿真计算过程中，针对爆炸螺栓装药量、爆炸螺栓分离端面尺寸变化工况建立6个计算模型，其中装药量偏差包括上偏差、中间值和下偏差3种工况。爆炸螺栓分离端面尺寸包括上偏差和下偏差两种工况。爆炸螺栓断裂端面尺寸位置如图5所示，此位置在爆炸分离过程中受到剪切、拉伸的作用而断裂。工况组合情况如表1所示。药量上偏差与中间值之间差值为3.83%，中间值与下偏差之间差值为3.75%；断裂端面尺寸上下偏差之间差值为12.7%；预紧力上下偏差之间差值为3.7%。爆炸分离过程仿真分析采用ABAQUS有限元软件，仿真模型结构示意图如图6所示。飞行器上共包括3组爆炸螺栓分离装置，所以在有限元分析过程中采用1/3模型进行计算，对航天器整体结构在分割面处建立周期性边界。飞行器相互连接面以及爆炸螺栓与螺母连接面采用TIE约束，各部件之间的相互作用定义为通用接触。

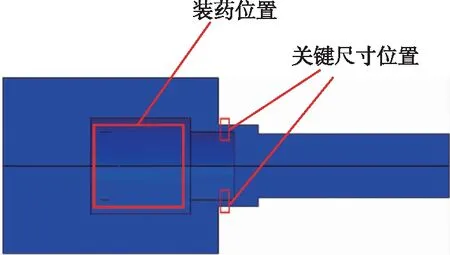
图5 爆炸螺栓断裂端面尺寸

表 1 爆炸螺栓组合工况

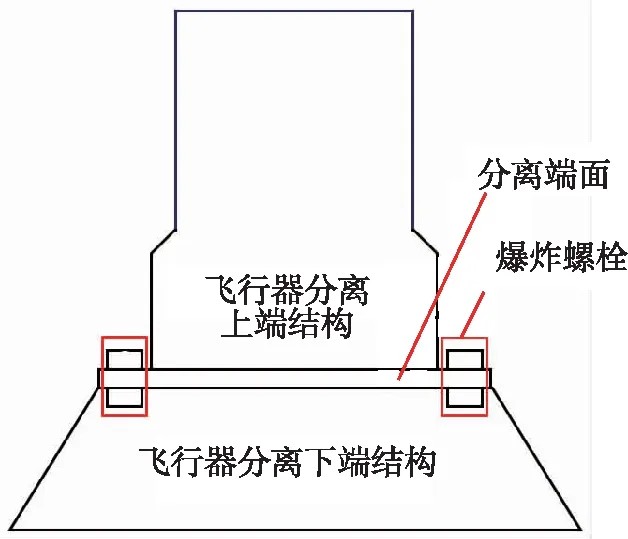
(a)飞行器及爆炸螺栓结构示意图

1.2.4 材料属性

飞行器分离装置中爆炸螺栓材料为高强钢，其Johnson-Cook本构模型具体参数如表2所示。炸药材料为TNT，材料参数采用JWL状态方程进行描述，具体参数如表3所示。

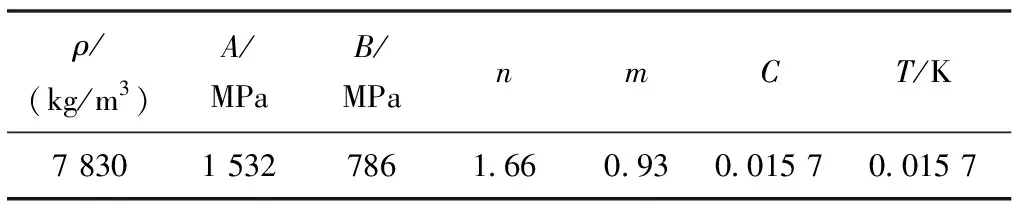
表2 爆炸螺栓材料Johnson-Cook本构参数[14]

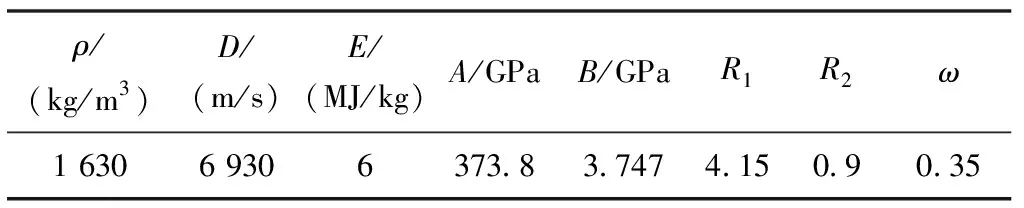
表3 TNT材料JWL状态方程参数

1.3 计算结果

在本文的仿真计算模型中，飞行器上共设置两个关键位置的测点，测点位置如图7所示，测点1位于飞行器与爆炸螺栓接触的分离端面上，测点2位于飞行器舱体母线位置，提取仿真结果的X，Y，Z这3个方向的加速度时域曲线，转化为3个方向的冲击响应谱。其中X方向为飞行器轴向，YZ平面为飞行器分离端面。

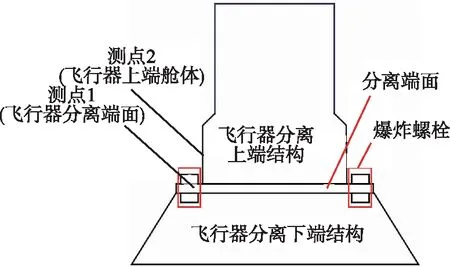
图7 飞行器测点位置

飞行器分离过程测点1的药量偏差工况的冲击响应谱如图8所示，在药量最大提升7.8%的情况下，在X方向上冲击响应谱100～5 000 Hz范围内表现出明显的差异，谱加速度最大差值在频率为2 016 Hz情况下为9 046g，上偏差工况约为下偏差工况的560%。差值约为15.0 dB。X方向为飞行器轴向，在爆炸螺栓药量增加后，直接增加了爆炸过程产生的能量，在此方向上药量的变化对冲击响应谱的影响显著。而在Y方向上，药量降低时，在某些频率范围下，冲击响应谱的值反而出现升高。爆炸螺栓不同药量下断裂面形态如图9所示，随着药量的下降，爆炸螺栓断裂面应力减少，脆性断裂趋势减少，此时爆炸螺栓的断裂面处呈现出明显的不平整。因此在药量下降时，爆炸螺栓由于断裂不彻底导致断裂后螺栓向Y方向偏离，在Y方向上对飞行器结构产生冲击，飞行器的结构响应导致在药量降低时，在某些频率下冲击谱加速度提高，因此在Y方向的上冲击响应谱曲线与X方向展现出不同趋势。

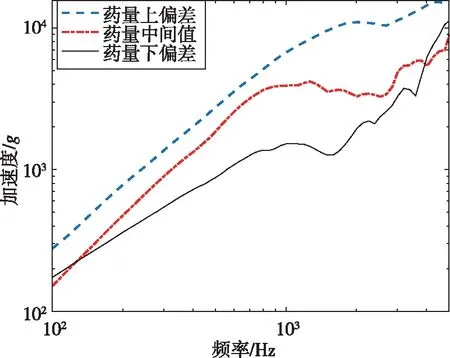
(a)测点1-X方向药量偏差

(a)药量上偏差工况螺栓断裂面

测点1的断裂端面尺寸偏差工况的冲击响应谱如图10所示。在X方向上，爆炸螺栓断裂端面尺寸上下偏差之间的冲击响应谱响应最大差值为6 040g，上偏差工况约为下偏差工况的11%,差值的绝对值约为19.4 dB; 在Y方向上，断裂端面尺寸上下偏差之间的冲击响应最大差值为1 626g，上偏差工况约为下偏差工况的64%,差值的绝对值约为3.9 dB; 在Z方向上，断裂端面尺寸上下偏差之间的冲击响应最大差值为2 216g，上偏差工况约为下偏差工况的40%,差值的绝对值约为8.0 dB。爆炸螺栓断裂端面尺寸下降会导致冲击响应谱的提升。尺寸变化对冲击响应加速度产生的影响包括两个方面：首先是爆炸螺栓断裂后断裂位置的预应力释放，断裂端面尺寸越大会导致断裂后释放的预应力越大，对飞行器结构产生更大冲击；此外，爆炸螺栓断裂后其头部向上飞行，会对飞行器上的爆炸螺栓回收罩产生冲击，这种情况下，断裂端面尺寸越小，会导致断裂后爆炸螺栓头部向上飞行速度越大，对回收罩产生的冲击越大。爆炸螺栓断裂后其头部位置向上飞行的速度云图如图11所示，断裂端面尺寸下偏差工况螺栓头部的冲击速度比上偏差工况大11.5%左右，使得爆炸螺栓解锁后对回收罩的冲击更大，这也表明在断裂端面尺寸变化时，头部的冲击速度是影响飞行器所受冲击响应的主导因素。因此在断裂尺寸更小的情况下，飞行器的冲击响应谱加速度值越大。

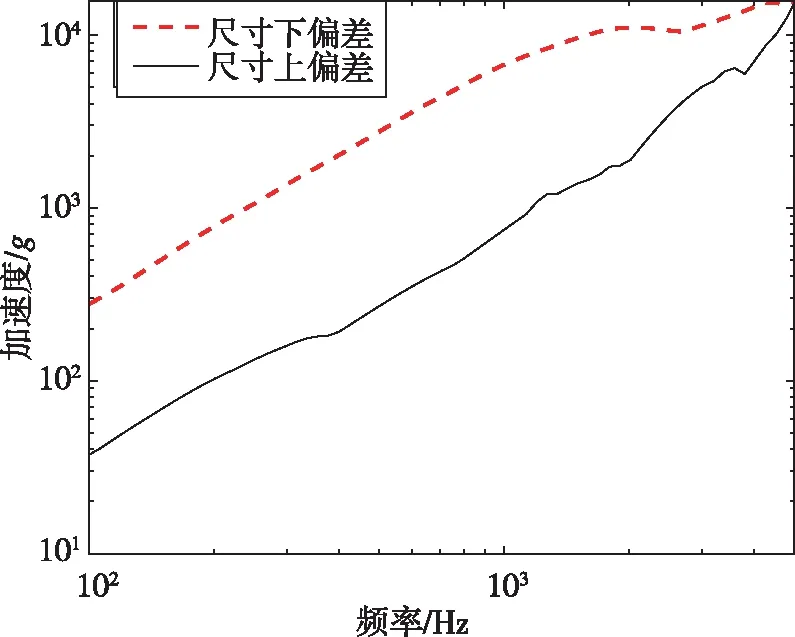
(a)测点1-X方向断裂端面尺寸偏差

(a)断裂断面尺寸上偏差

各测点在不同药量和断裂端面尺寸的冲击响应谱加速度最大差值如表4和表5所示，药量和尺寸对测点2冲击响应的影响与测点1类似。

表4 不同药量下各测点最大差值

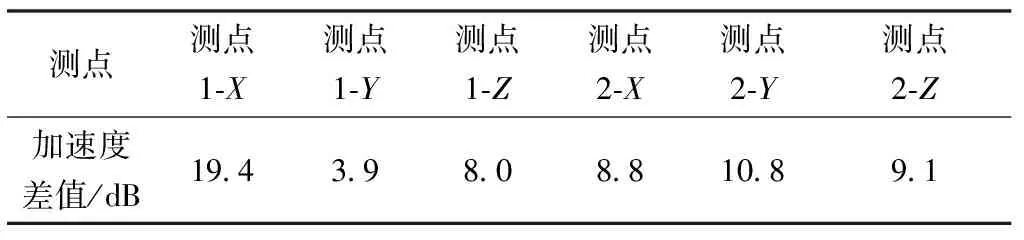
表5 不同断裂端面尺寸下各测点最大差值

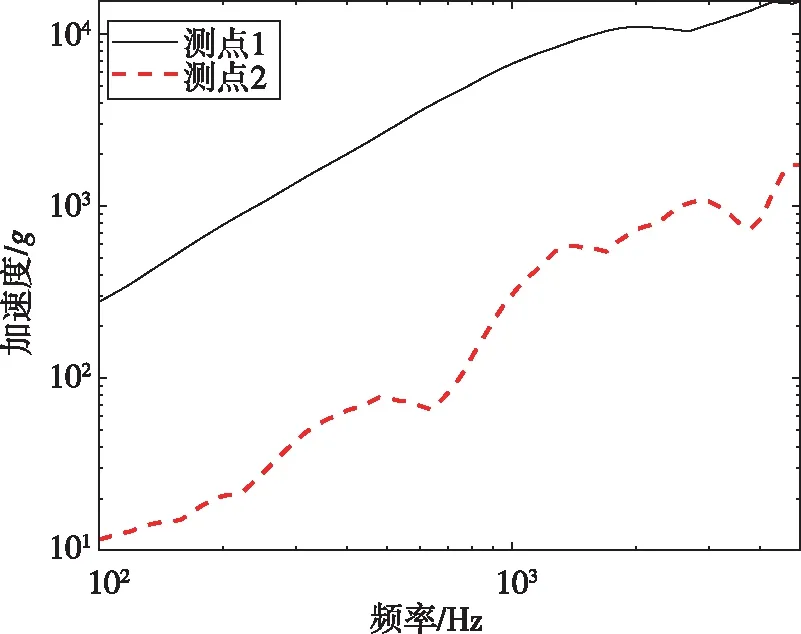
测点2位于飞行器舱体外壁上，舱体与爆炸螺栓分离端面连接。测点2与测点1的冲击响应谱对比如图12所示，冲击波经过不同结构的衰减后，冲击响应谱在各个频率下的加速度响应均出现明显衰减。冲击响应与设备和爆炸螺栓的间隔距离成反比，测点1加速度峰值为测点2的10倍以上，这为飞行器关键设备的安装位置提供设计思路。

(a)X方向冲击响应谱对比

2 结论

本文建立了飞行器爆炸分离仿真模型，通过CEL计算方法研究爆炸螺栓分离装置在解锁过程中对飞行器造成的冲击响应，依据单发爆炸螺栓实验对计算方法进行了验证。研究了不同设计参数对冲击响应的影响规律，得出以下结论：

1)通过CEL计算方法可以较为准确地模拟飞行器分离过程中爆炸螺栓的解锁进程。

2)爆炸螺栓药量增大对不同方向的冲击响应谱影响不同。爆炸螺栓中装药量的增加直接引起爆炸能量提高，导致飞行器轴向(X方向)的冲击响应谱明显增大。药量降低会导致爆炸螺栓断裂困难，引起爆炸螺栓在分离端面上移动，对飞行器结构产生撞击，导致Y，Z方向冲击响应谱在某些频率范围内增大。

3)断裂端面尺寸减小导致冲击响应谱增大。爆炸螺栓断裂端面尺寸的减小会导致解锁后螺栓头部向上飞行的速度增大，对回收罩产生的冲击增大，与断裂部位的预应力释放相比较，螺栓分离部分飞行速度增大是引起冲击响应谱变化的主要原因。

4)冲击响应随着设备距爆炸螺栓位置的距离增加明显下降。