高速铁路大跨度连续梁桥竖向共振现象研究

王韫璐 高芒芒 高彦嵩 简方梁 孟鑫

1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；3.中国国家铁路集团有限公司 科技和信息化部，北京 100844；4.中铁工程设计咨询集团有限公司，北京 100055；5.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081

为保证高速铁路对线路平顺性的要求及减少占地，我国高速铁路大量采用以桥代路。列车经过桥梁时，可将列车视为由轴重组成的移动荷载列，当加载频率与桥梁的自振频率接近时会引起桥梁共振［1-2］，进而引发道床不稳定、钢轨损伤、混凝土梁开裂等问题［3］。连续布置的桥跨结构会对列车形成一定频率的周期性作用，如果此频率接近车辆的自振频率，车辆就会出现共振现象［4-5］，影响列车的行车安全性和稳定性，同时增大对桥梁的动力冲击作用。

国内外大量研究表明，梁体竖向自振频率、列车运行速度、车辆长度、结构阻尼、轨道平顺性等是影响车桥动力响应的因素［3，6］。TB 10621—2014《高速铁路设计规范》［7］通过控制常用跨度简支梁的竖向自振频率，避开由于列车荷载产生的竖向加载频率，控制梁体竖向共振的发生。而连续梁的振动模态比简支梁复杂，竖向动力响应由多阶模态决定，在运营过程中可能会出现动车组以共振速度通过桥梁的情况。在实际工程应用中，受地理环境因素等限制，连续梁跨度布置可能会落在列车的共振敏感波长范围内，引起车桥系统共振。

本文以（40+64+40）m 连续梁桥为例，结合连续梁桥的实测自振频率、主要型号列车的实测竖向加速度以及车桥动力响应，分析车桥系统出现共振现象的原因以及共振对列车运行的影响，并基于规范对系统的动力响应进行评价，可为桥梁设计优化、评价标准完善、铁路工务检养修等提供依据。

1 车桥系统共振理论

1.1 桥梁共振

由于轴重荷载的规律性排列，列车会对桥梁产生不同频率的周期性动力作用。以四轴车为例，其荷载排列如图1（a）所示。其中，lw为固定轴距，lc为车辆定距，lv为车辆钩到钩距离，Lb为桥梁跨度，V为列车速度。若把前一节车的后转向架与后一节车的前转向架对桥梁的荷载作为一个整体，可将列车轴重作用力简化成间距为lv的等间距移动集中力荷载列P进行分析，如图1（b）所示。

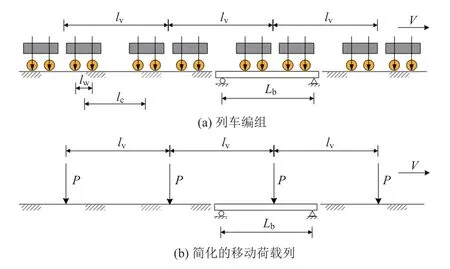
图1 列车通过桥跨时的荷载作用

列车对桥梁的动力作用相当于频率为V/lv的周期性荷载。当此频率接近桥梁的第n阶自振周期或i次谐波周期时，桥梁就会出现共振现象［8-9］。引起桥梁共振的列车临界速度，即共振车速Vbr［4］为

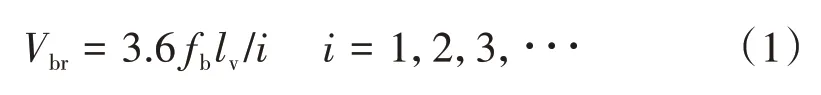
式中：fb为桥梁的竖向自振频率。

我国高速铁路设计速度为250～350 km/h，动车组钩到钩长度为25 m，根据式（1）得到桥梁共振频率为2.78～3.89 Hz。调研我国京津城际铁路、武广客运专线和京沪高速铁路典型桥梁的实测竖向自振频率，结果见表1。可知，桥梁实测竖向自振频率在2.78～3.89 Hz的桥式方案仅有（40+56+40）m连续梁和（40 +64+40）m连续梁。

表1 我国部分高速铁路桥梁的实测竖向自振频率

不同图号（40+64+40）m 连续箱梁的实测竖向自振频率见表2。可知，在高速列车运营速度范围内，主跨64 m 连续箱梁的第一阶竖向自振频率均在桥梁共振频率范围内，可能发生竖向共振。

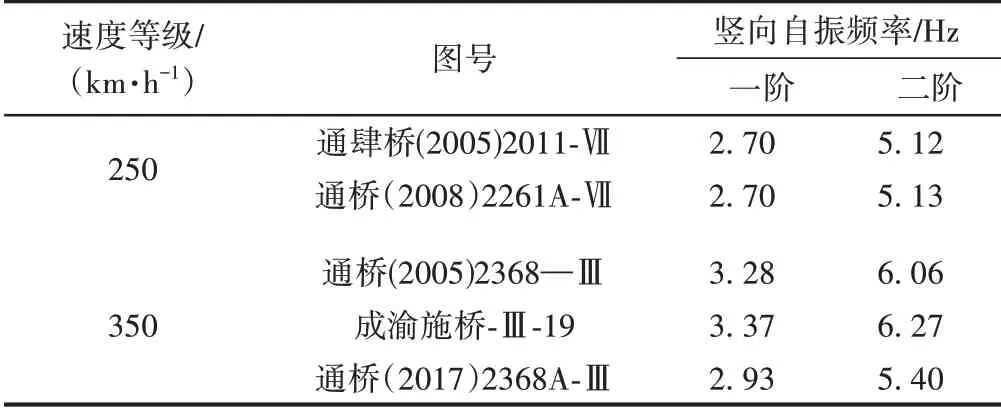
表2 不同图号（40+64+40）m连续箱梁的实测竖向自振频率

1.2 车辆共振

列车通过桥梁时，如果桥跨连续布置，其挠度会对车辆形成周期性不平顺，当不平顺的频率与车辆自振频率接近时可能会引发车辆的共振［10］。引发车辆共振的桥梁跨度Lb计算式［6］为

式中：Vvr为列车速度；fv为车辆的自振频率。

对我国运营的几种主型车辆竖向加速度进行统计分析，车速为300 km/h 时功率谱密度见图2。可知，低频段车体竖向加速度空间频率集中分布在0.013 7～0.015 6 m-1，对应列车竖向敏感波长为64～73 m。

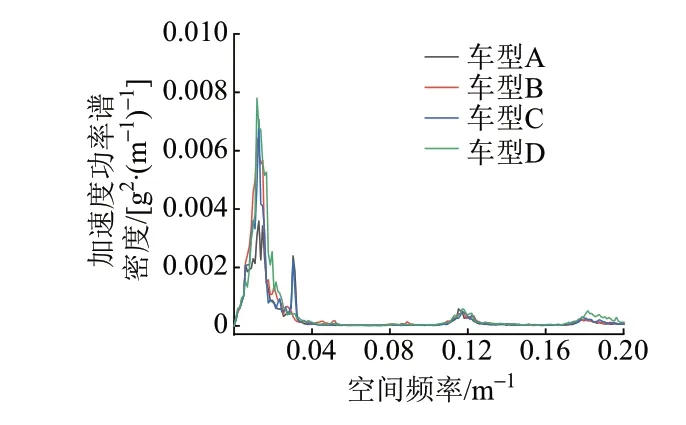
图2 运营列车的竖向加速度功率谱密度

同一型号列车的敏感波长与列车速度成正比［6］，由此可以推断列车速度为250、300、350 km/h 时的竖向敏感波长分别为53～61、64～73、75～85 m。可能造成车辆共振的波长为53～85 m。车辆的共振响应需要周期性波长激励，而53～85 m 跨度的桥梁通常为连续梁桥，并且较少连续布置，因此车辆共振的风险比桥梁共振小。

综上，主跨56、64 m 连续箱梁较易发生共振效应。因此，本文以（40+64+40）m 连续箱梁为例做进一步分析。

2 动力响应评判标准

TB 10621—2014 中规定除简支梁外的其他结构类型桥梁应按实际情况进行车桥耦合动力响应分析。无砟桥面的振动加速度限值为5.0 m/s2。

TG/GW 209—2014《高速铁路桥梁运营性能检定规定（试行）》［11］中给出了常用跨度预应力混凝土双线箱梁的竖向自振频率通常值（下限）和梁体跨中竖向动力响应通常值（上限）等。无砟轨道64 m 预应力混凝土双线连续箱梁的动力响应通常值见表3。

表3 无砟轨道64 m 预应力混凝土双线连续箱梁的动力响应通常值

GB/ T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》［12］中车辆动力性能指标限值见表4。

表4 车辆动力性能指标限值

3 连续梁共振现象分析

3.1 工程概况

以设计速度350 km/h 的（40+64+40）m 连续箱梁为例进行分析。该桥轨道形式为CRTSⅢ型板式无砟轨道，根据动态检测结果，在速度为260 km/h 的动车组作用下中跨跨中的竖向振幅为0.71 mm，超出TG/GW 209—2014中规定的通常值。

不同类型连续箱梁竖向动力响应对比见表5。可知，与既有高速铁路的相同跨度桥梁（采用的通用图号与本文连续箱梁不同）相比，本文连续箱梁竖向振幅偏大，竖向自振频率偏低。此外，该连续箱梁的竖向阻尼比为0.6%，显著低于通常预应力混凝土简支箱梁实测阻尼比2.0%［13］。

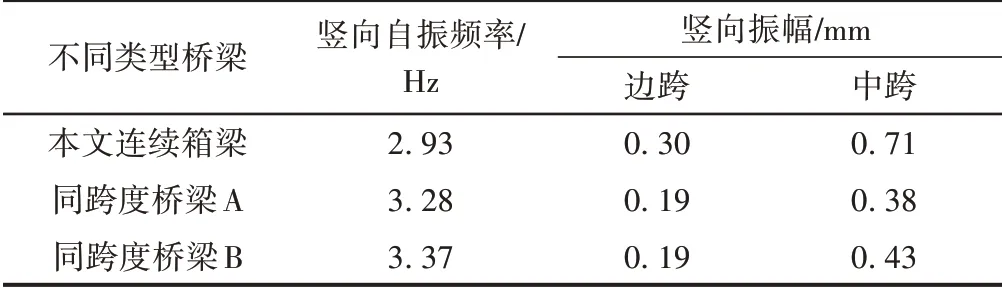
表5 不同类型连续箱梁竖向动力响应对比

该连续箱梁设计采用通用图（通桥（2017）2368A⁃Ⅲ⁃1），主要设计参数见表6。可知，该通用图与2005、2008版相比，桥面宽度、顶板厚度、腹板厚度、梁高、梁重等均略有调整。

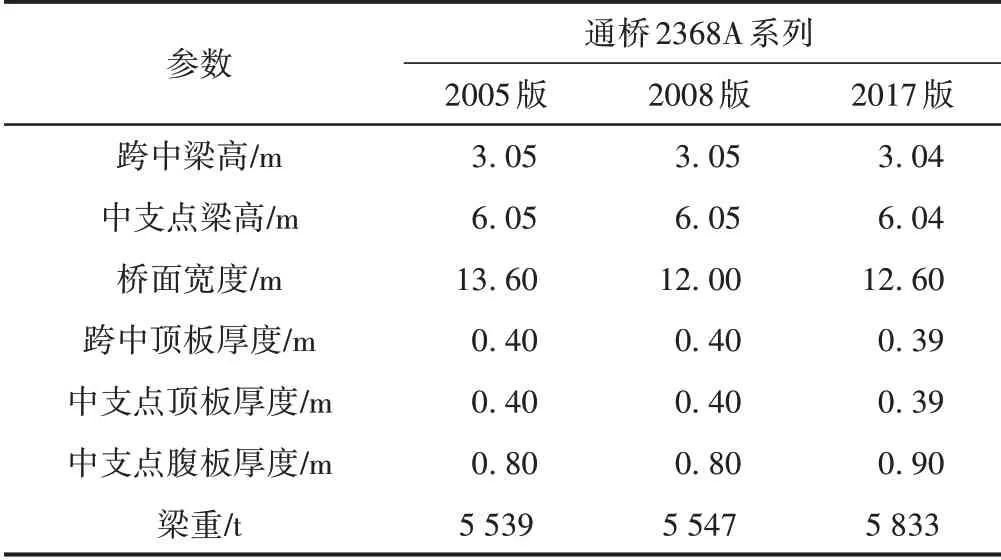
表6 通桥2368A系列连续箱梁结构尺寸对比

鉴于TG/GW 209—2014 中的通常值是针对2014年以前的实测数据样本通过统计分析得到的上限值，并未涵盖此梁型。因此，分别采用该连续箱梁的实际参数和通用图设计规范中的参数建立车桥耦合动力模型，研究桥梁和列车的动力响应，分析振幅超限原因。

3.2 动力分析模型

3.2.1 桥梁模型

1）连续梁模型

采用MIDAS 商业软件分别建立该连续梁实桥有限元模型和通用图有限元模型，主梁和墩台均采用空间梁单元模拟，墩底固结，桥梁支座处的约束条件采用主从节点处理。

实桥模型的二期恒载采用实际值124.2 kN/m，竖向阻尼比为0.6%。桥梁的实测一阶竖向自振频率为2.93 Hz，二阶竖向自振频率为5.22 Hz。通过调整模型中主梁混凝土的弹性模量，使有限元模型的自振频率与实测值基本相同，调整后的模型一阶竖向自振频率为2.83 Hz，二阶竖向自振频率为5.23 Hz。

通用图模型（通桥（2017）2368A⁃Ⅲ⁃1）二期恒载采用设计值180 kN/m，阻尼比取2.0%，混凝土弹性模量按规范［14］取值。模型的一阶竖向频率为2.219 Hz，二阶竖向频率为4.140 Hz。

连续梁的竖向动力响应由多阶模态共同决定，当竖向强振频率与梁体某阶自振频率接近时，梁体竖向动力响应会出现峰值。峰值与该阶频率对应的振型有关［15］。连续梁前两阶竖向振型分别为对称和反对称振型，见图3。

图3 （40+64+40）m连续梁前两阶竖向振型

2）桥梁系统动力方程

桥梁系统的运动方程为

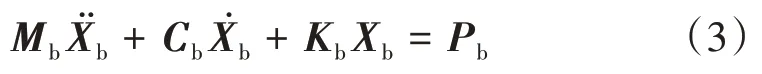
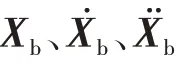
3.2.2 车辆模型

该桥实际运营的列车为高速动车组，16 节编组（1 拖+14 动+1 拖），最高设计速度为350 km/h。车辆系统的运动方程为

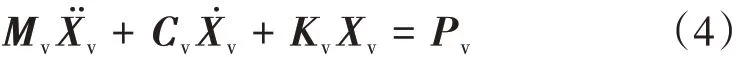
3.2.3 轨道不平顺

选择设计速度为350 km/h 的运营高速铁路实测轨道不平顺数据作为输入不平顺样本，长度为2 km，截止波长为70 m。

3.2.4 轮轨作用力及动力方程求解

车辆、桥梁通过轮轨相互作用形成耦合系统［16-17］，法向轮轨力采用Hertz 非线性接触理论求解。本文采用逐步积分法对耦合运动方程进行求解，在每一迭代步中将桥梁变形与轨道变形叠加形成新的不平顺后进行计算，直到满足迭代精度要求。

3.3 动力响应分析

3.3.1 连续梁实桥动力仿真分析

1）桥梁振动响应

实桥模型连续梁跨中最大竖向动态响应见表7。可知，各车速下的桥梁跨中振动加速度均满足TB 10621—2014 要求，但超出了TG/GW 209—2014 中竖向振动加速度的通常值。当列车以260 km/h 的速度运行时，该连续梁的竖向动位移和竖向加速度明显高于其他工况。

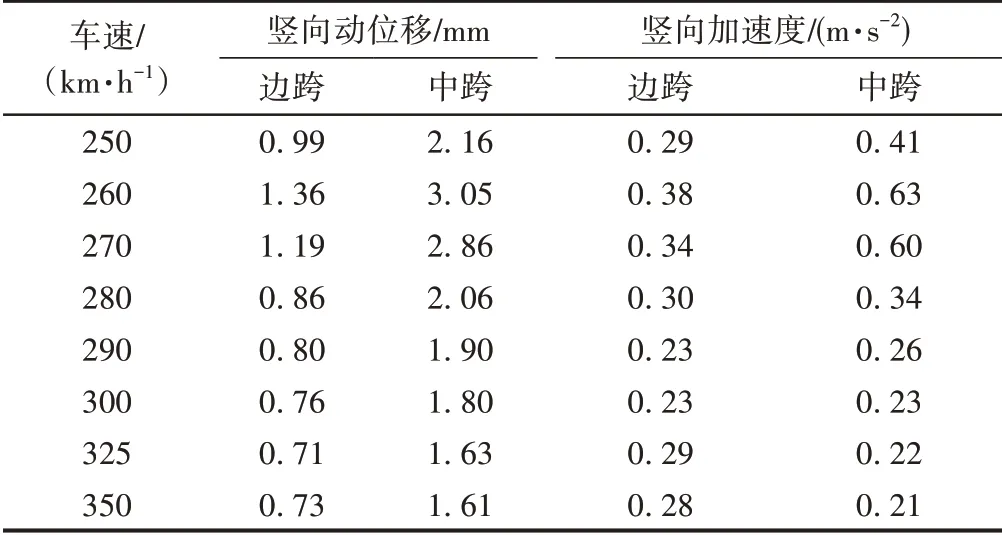
表7 实桥模型连续梁跨中最大竖向动态响应

该连续梁实测一阶竖向自振频率为2.93 Hz，理论分析一阶竖向自振频率为2.83 Hz，可得竖向共振车速接近260 km/h。实桥模型桥梁跨中竖向动位移、竖向加速度时程曲线分别见图4 和图5。可知，当车速为260 km/h 时，桥梁边跨和中跨的竖向动位移和竖向加速度比其他两种车速下的结果显著增大，说明桥梁发生竖向共振。由于桥梁的自重较大，共振情况下桥梁边跨和中跨的竖向振动加速度均不超过0.8 m/s2，远小于5.0 m/s2的规范限值，可判定轨道结构不会因桥梁共振而发生失稳。

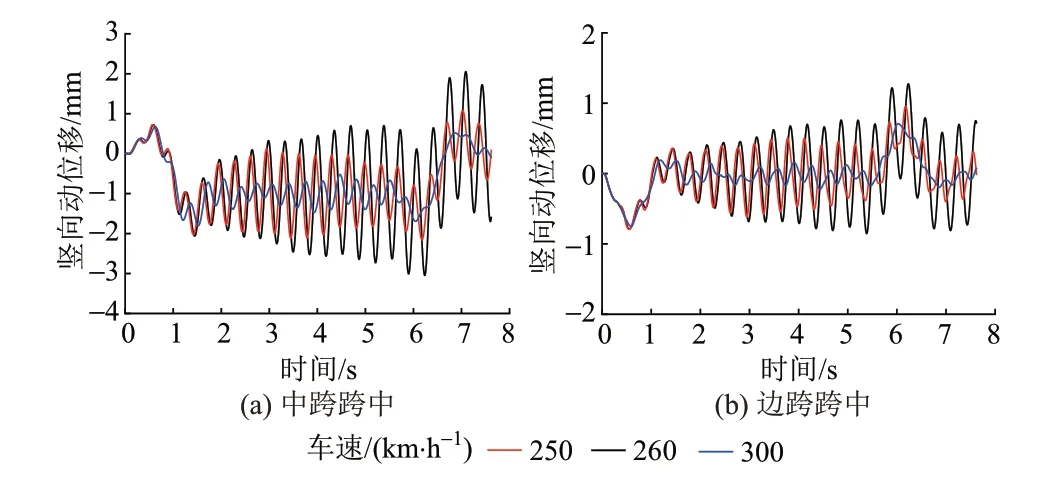
图4 实桥模型桥梁跨中竖向动位移时程曲线

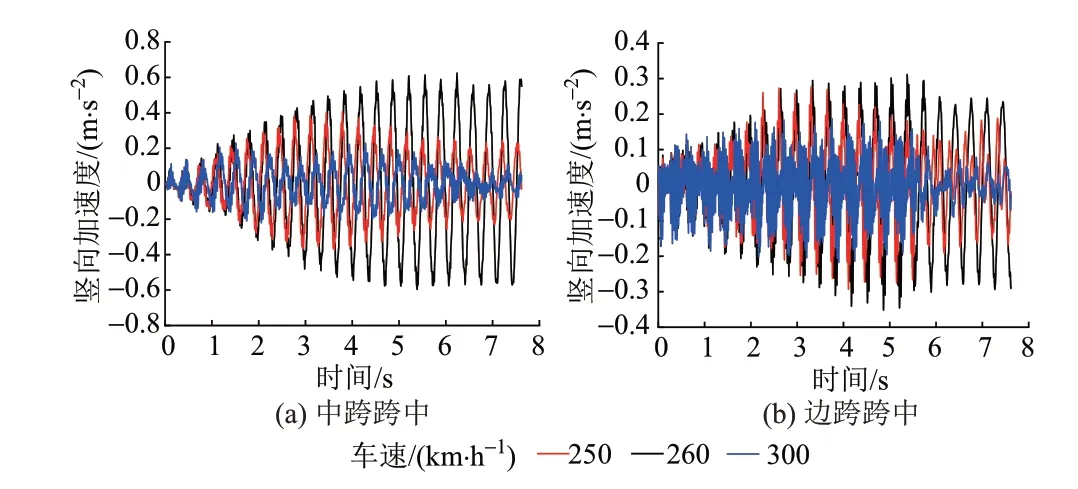
图5 实桥模型桥梁跨中竖向加速度时程曲线

2）车辆振动响应

实桥模型不同车速下车辆最大动力响应见表8。可知，250～350 km/h速度范围内的列车最大动力响应均满足规范要求。不同车速下列车的竖向加速度响应差异很小，说明在该速度范围内没有发生车辆共振现象。虽然该连续梁跨度落在列车竖向敏感波长范围内，但桥跨结构没有连续布置，因此车辆没有受到周期性的激励，车辆未发生共振。

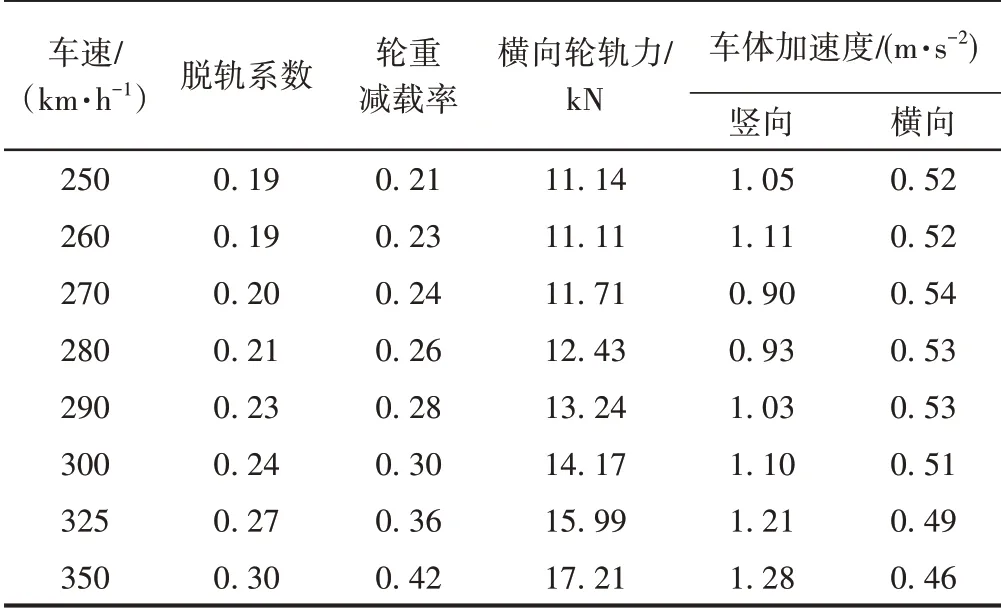
表8 实桥模型不同车速下车辆最大动力响应

3.3.2 连续梁通用图动力仿真分析

1）桥梁振动响应

通用图模型连续梁在不同车速下的跨中最大动力响应结果见表9。不同车速下的桥梁跨中振动加速度均满足TB 10621—2014 要求，但跨中竖向加速度仍超出了TG/GW 209—2014中的通常值。当车速在250～350 km/h时，桥梁的竖向动位移差异不大，并没有发生共振现象。

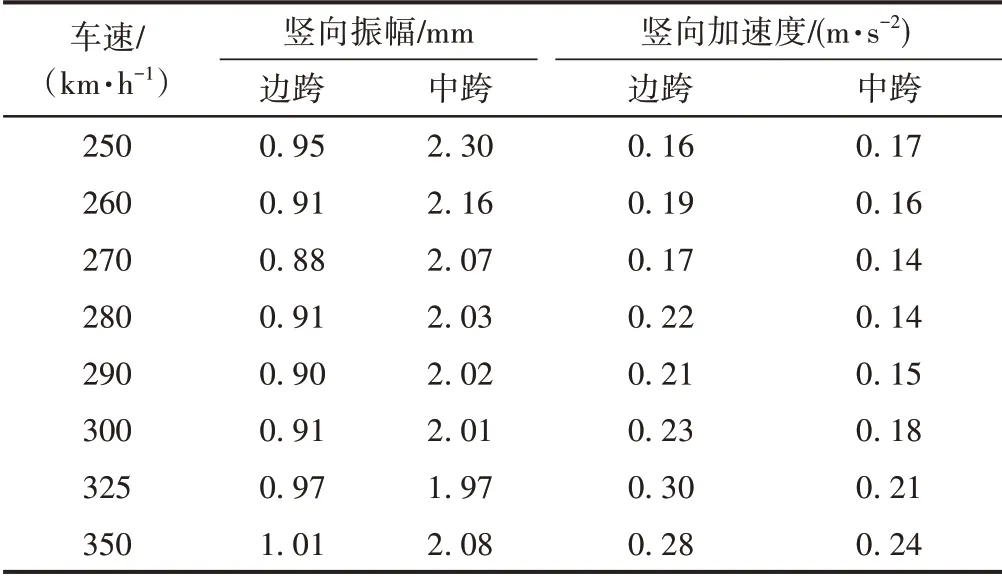
表9 通用图模型连续梁跨中最大竖向动态响应

通用图模型桥梁跨中竖向动位移、竖向加速度时程曲线分别见图6和图7。可知，不同车速下桥梁的竖向动位移和竖向加速度没有明显差异，说明在此车速范围内桥梁没有出现共振现象。通用图连续梁的前两阶竖向自振频率分别为2.219、4.140 Hz，推算前两阶共振车速为200、373 km/h，均在运营车速范围外。因此，当连续梁通用图中各项参数采用规范数值时，桥梁不会出现共振现象。

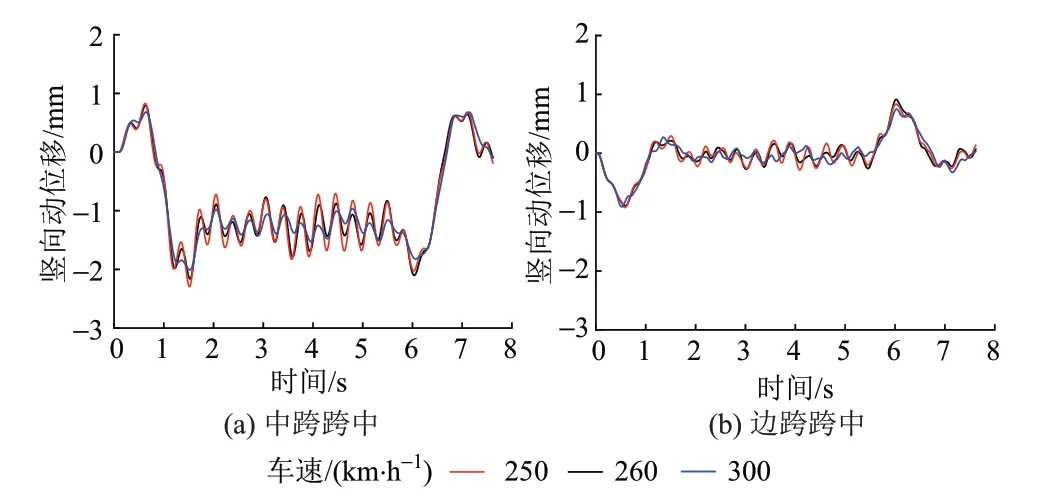
图6 通用图模型桥梁跨中竖向动位移时程曲线

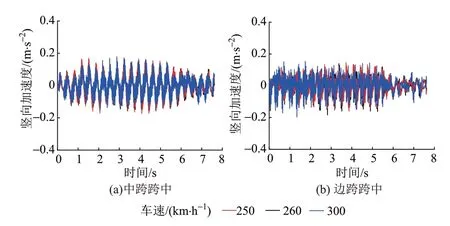
图7 通用图模型桥梁跨中竖向加速度时程曲线

2）车辆振动响应

通用图模型不同车速下车辆最大动力响应见表10。可知，250～350 km/h速度范围内的列车动力响应均满足规范要求。车辆的各项动力响应指标随车速增加而增大，并未出现在某一速度区间显著增大的情况。由于该连续梁桥跨结构没有连续布置，车辆并未受到周期性的激励，车辆未发生共振。

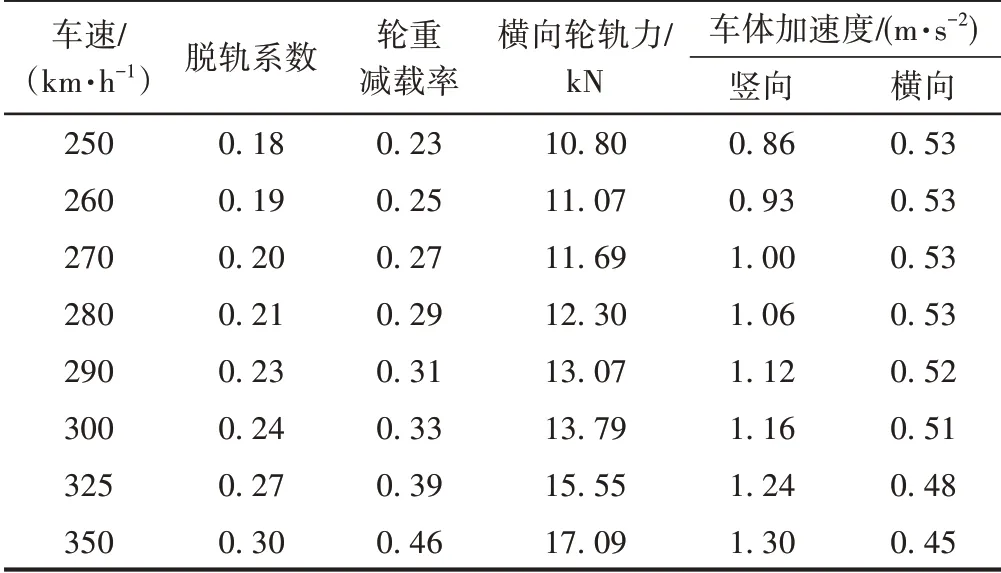
表10 通用图模型不同车速下车辆最大动力响应

虽然桥梁的竖向加速度超过了TG/GW 209—2014 规定的通常值，但桥面竖向振动加速度小于5 m/s2限值，轨道结构保持稳定。列车的振动响应均远小于限值，满足列车的行车安全性和平稳性要求。

4 结论

1）通过对我国高速铁路典型桥梁自振频率的调研和共振速度的分析，（40+56+40）m和（40+64+40）m连续梁可能由于列车荷载的周期性作用发生共振。

2）由于实桥自振频率通常与设计值存在差异，当实际桥梁的自振频率处于共振频率范围内时，建议根据实际桥梁的参数进行动力响应分析，评估桥梁结构的稳定性及列车的行车安全性和平稳性。

3）本文连续梁桥在车速260 km/h 时出现了桥梁结构的共振响应，但桥面振动加速度满足规范要求，轨道结构保持稳定，车辆未发生共振，与实测规律一致。