基于分形几何的BIM地形模型轻量化研究
2022-02-07李勇段晓峰王宏远
李勇 段晓峰 王宏远
兰州交通大学 土木工程学院,兰州 730070
铁路线路地形具有长带状特征,现有的BIM 和GIS(Geographic Information Science)软件使用过程中地形模型数据量过大且冗余过多,导致加载缓慢或长时间无法响应。若大范围删减,又可能因删减不当导致数据点无法较好地表征实际地形特征;同时,构网方式单一化,无法满足工程多式样的地形显示。
在地形建模和轻量化研究方面,王倩[1]研究了三角形网格地形建模的基本方法和理论,包括规则数据及不规则数据三角网的生成算法。文雄志[2]运用层次细节技术和基于网格的模型简化技术对三维地形建模进行简化,使其能够更好地实现建模简化技术的应用。陆风等[3]对基于地形线的Memoryless 改进算法的简化效果进行了验证,显示水下地形模型简化后保持了原有特征和细节,但模型会产生跳跃现象。宋伟华等[4]通过Delaunay 逐点插入算法构建TIN 模型,该算法能用更少的数据表达复杂地表形态,但时间复杂度差、运行速度慢。分形理论的出现和发展,为描述自然界的复杂事物提供了解决思路。李鑫[5]利用数字图像处理技术实现了获取分形维数的流程,具有较好的测量稳定性,无需占用太多计算机资源即可获得较高精度。张欣悦等[6]提出利用有理分形插值进行分形曲线建模,验证了可变参数的有理分形插值曲线在处理实际问题中具有较好的应用价值。彭晓蕾等[7]对蕴含地貌特征的黄土高原地貌数据进行分形设计,将自然景观特征与公式化的数学思维相结合,为自然景观的美学研究提供了一个新的方向。
鉴于分形算法由极少部分地形控制点就可表达出原地形的特征,还能在保持地形真实感的状态下根据实际需求动态控制地形的细化程度,在地形构网上具有优越性,因此本文尝试基于分形算法解决BIM 地形模型轻量化表达问题。
1 分形理论概述
1.1 分形的概念及维数
若集合F在欧氏空间中的Hausdorff 维数DH恒大于其拓扑维数Dr,即DH>Dr,则该集合是分形集,简称分形[8-9]。分形维数是一种非整数维数,用来解决整数维在尺度上出现过大或过小而无法准确评价的问题。如果将分形拓展到表示自然界中的行为或现象,那么分形维数描述的则是零碎的局部特征构成整体系统行为的相关性。
1.2 地形分形维数的计算
地形分形维数计算常用的方法为表面积-体积法和方差图法。
1.2.1 表面积-体积法
用Hausdorff 面积SH表示地形面积,V表示地形曲面的体积。由量纲分析可得

式中:D为地形曲面的分形维数。
若用S表示地形曲面的欧式面积,则有

式中:k0为系数,又称形状因子;l为尺度值。
则可推导出直接计算分形维数的公式为

1.2.2 方差图法
方差图法是建立在图像(分形数据)的高斯统计模型上的。给定一个分形维数D和方差δ,用分形布朗运动(Fractional Brownian Motion,FBM)模型可模拟生成一幅图像。反之,如果将图像或地形表面看成是分形布朗曲面,就可以得到其FBM模型的分形维数。
2 基于分形理论的数字地形模型生成算法
用于地形模拟的分形算法主要为基于迭代函数系统(Iterated Function System,IFS)方法和基于分形布朗运动(FBM)方法[9-10]。IFS 方法是对已有数据集进行仿射变换,构造一类插值函数,进而通过迭代过程,得到需要的形状。FBM 方法通过控制表征值H、δ等参数,加入随机变量然后构造出所需的分形图形[11]。本文采用基于FBM的方法对地形进行重构。
FBM 是一种随机过程,其增量按正态分布[12-13]。将FBM 二维曲面定义为在某概率空间上的随机过程,且满足:X(0,0)=0,X(x,y)是(x,y)的连续函数。
对任意变量(x,y),(h,k) ∈R2,其二维增量X(x+h,y+k) -X(x,y)服从期望为0,方差为(h2+k2)2H的正态分布,其概率满足
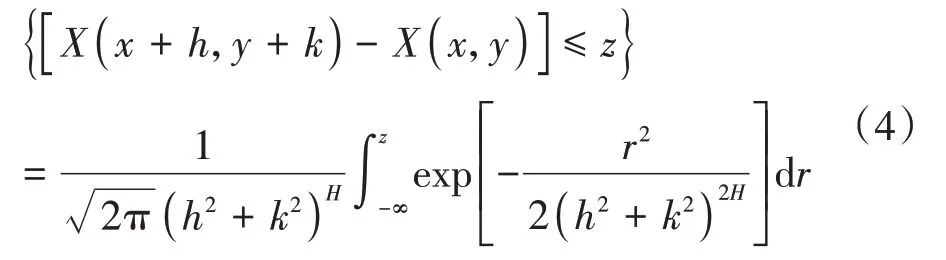
基于FBM 的插值方法主要有泊松阶跃法、随机中点位移法(Random Midpoint Displacement,RMD)、傅立叶滤波法、逐次随机增加法等[13]。本文采用基于FBM的改进随机中点位移法,通过对OpenRail 软件二次开发以改进优化原有地形生成时的臃肿情况。
中点位移法是标准的分形几何法,其在细分过程中,通过对两个或多个顶点之间插值进行地形建模,具有高速度以及为已有形状增加细节的能力,但在实际生成地形过程中地形曲面会出现褶皱现象。为此采用一种加入与分形特征表征值H、σ相关的补偿项的改进随机中点位移法。该方法既能满足用分形布朗运动特征的分形表面来表达自然地形,同时又能很好解决此问题[14-16]。
设01,02,…,0n为初始栅格数据点,格网间距为d0。每一级细分包括两步内插过程。
1)第一步:diamond步
由最邻近的四个格网点高程h0i(i=1,2,3,4),内插其中心点h1i的高程。高程值等于四个格网点高程的平均值加上一个随机位移Δ ∼N(0,V2∆)。h1i计算式为
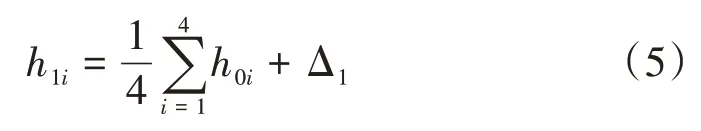
此时,原始的正方形格网旋转45°成为菱形格网,格网间距也由d0变为d1,即

2)第二步:Square步
由第一步得到的已知菱形四个角点高程内插其中心点高程,即
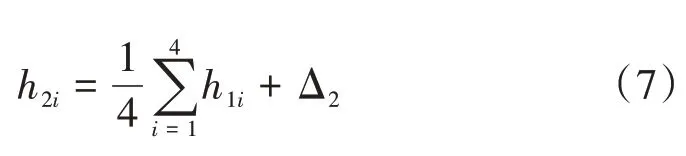
经过第二步,格网间距又变为d2,即

如此,随机中点位移法的一个完整步骤就完成了,如图1所示,接着按照所需迭代次数反复进行迭代计算就可得到所需的分形曲面。但存在随机变量的取值问题。通常,对Δ 的选择要使待插点的高程增量满足FBM 所需的幂指数规律。令格网间距的变化尺度为γn(n为迭代水平),那么随机位移的方差为
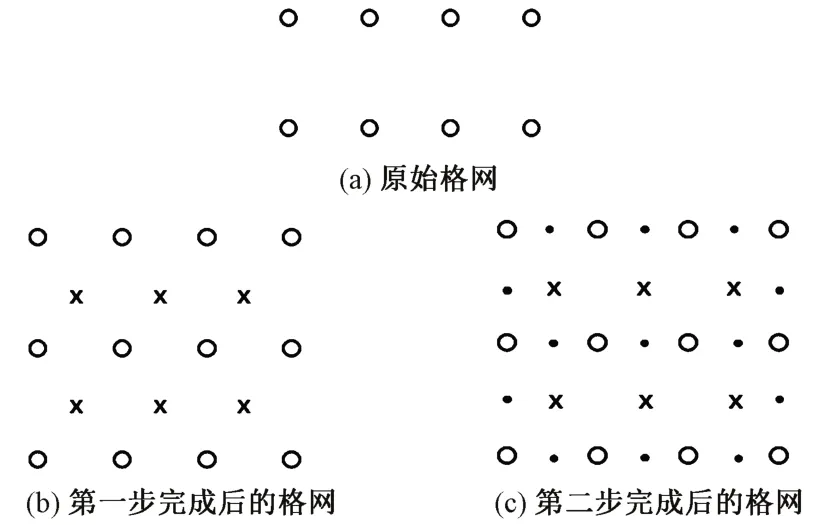
图1 随机中点位移法计算示意

由d1和d2可知γ=2-n/2,因此演变出常用的随机位移公式,即

式中:sc为位移大小调整因子;G为高斯随机分量,G∼N(0,1)。
式(10)一般用于虚拟分形地形的生成,不适用于自然世界中实测数据的插值。为使待插点的分形特征符合实际数据的分形特征,Yokaya 提出了式(11)的随机位移增量。
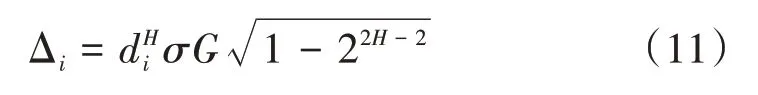
本文采用文献[9]提出的改进Yokaya 随机增量,即
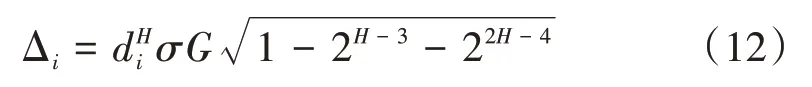
3 基于分形算法的地形模型重构技术
为了直接将分形地形与实际线路BIM 设计相结合,选用OpenRail Designer进行二次开发。
3.1 OpenRail二次开发环境搭建
本文所使用的软件及配置为:①操作系统为Windows10,内存16G,显卡GTX1650,显存8G;②编译平台为Visul Studio2015;③开发环境为.NET4.6.2 及以上版本的框架,与OpenRail版本匹配的SDK。
3.2 基于分形算法重构地形模型
3.2.1 原始数据重采样
本次地形数据采用无人机航测数据,在原有数据的基础上进行重采样,以满足算法需要。
由分形布朗运动相关知识可知,要计算分形维数D,需要不断改变其尺度。因此本文在提取分形特征值时,考虑实际地形数据特征,将采样间隔设置为20、40、50、60 m,且为判断不同轴采样对分形特征值的影响,分别沿数据的x轴、y轴和对角线采样,获得不同的采样结果,见图2、图3。

图2 高程点重采样
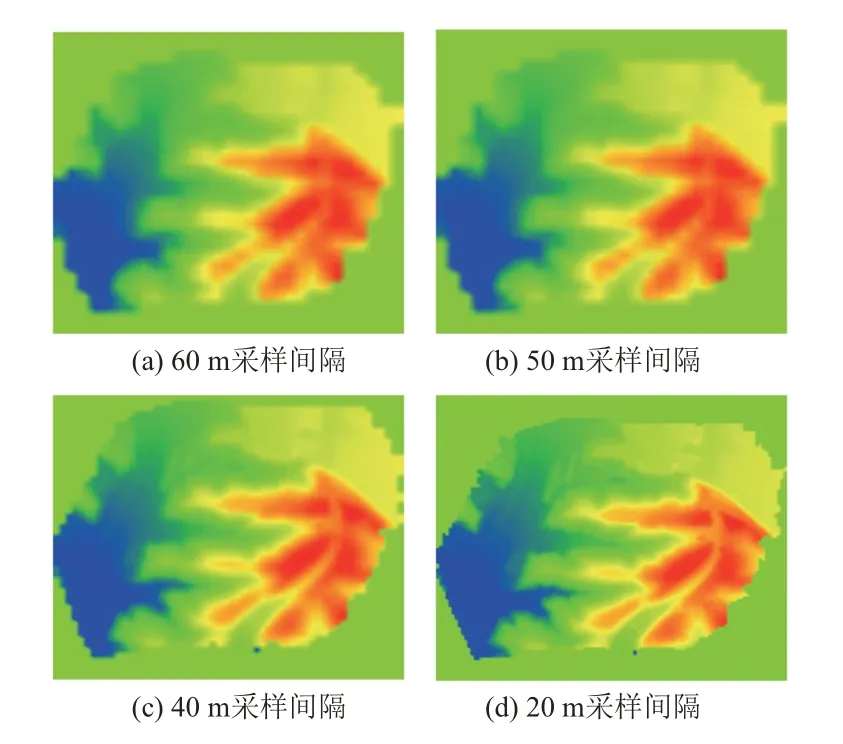
图3 重采样栅格图
3.2.2 分形特征提取
假设f(x)为一个随机分形布朗运动,则满足式(13)的概率分布函数[14-15]。

式中:f(x)为采样值;Δx为采样间隔;H为频谱指数;F(y)为累积概率分布函数,服从标准正态分布(0,δ2)。而分形维数D=N+1-H,N为拓扑维数。对地形曲面进行分形模拟时,H表示地形复杂情况的一种抽象和概括,H越大分形布朗运动变化趋于平缓,H越小变化趋于精细;δ反映地形曲面的起伏特征。
式(13)又可改写为

最小二乘法的直线回归函数为

由此求得系数H、C,便可推得D和δ。
为比较采样方向对地形特征的影响,将整体数据划分为四个大小一致的区块依次计算各分块分形特征值,用来比较区块分形特征值与整体分形特征值的差别,见图4、图5。
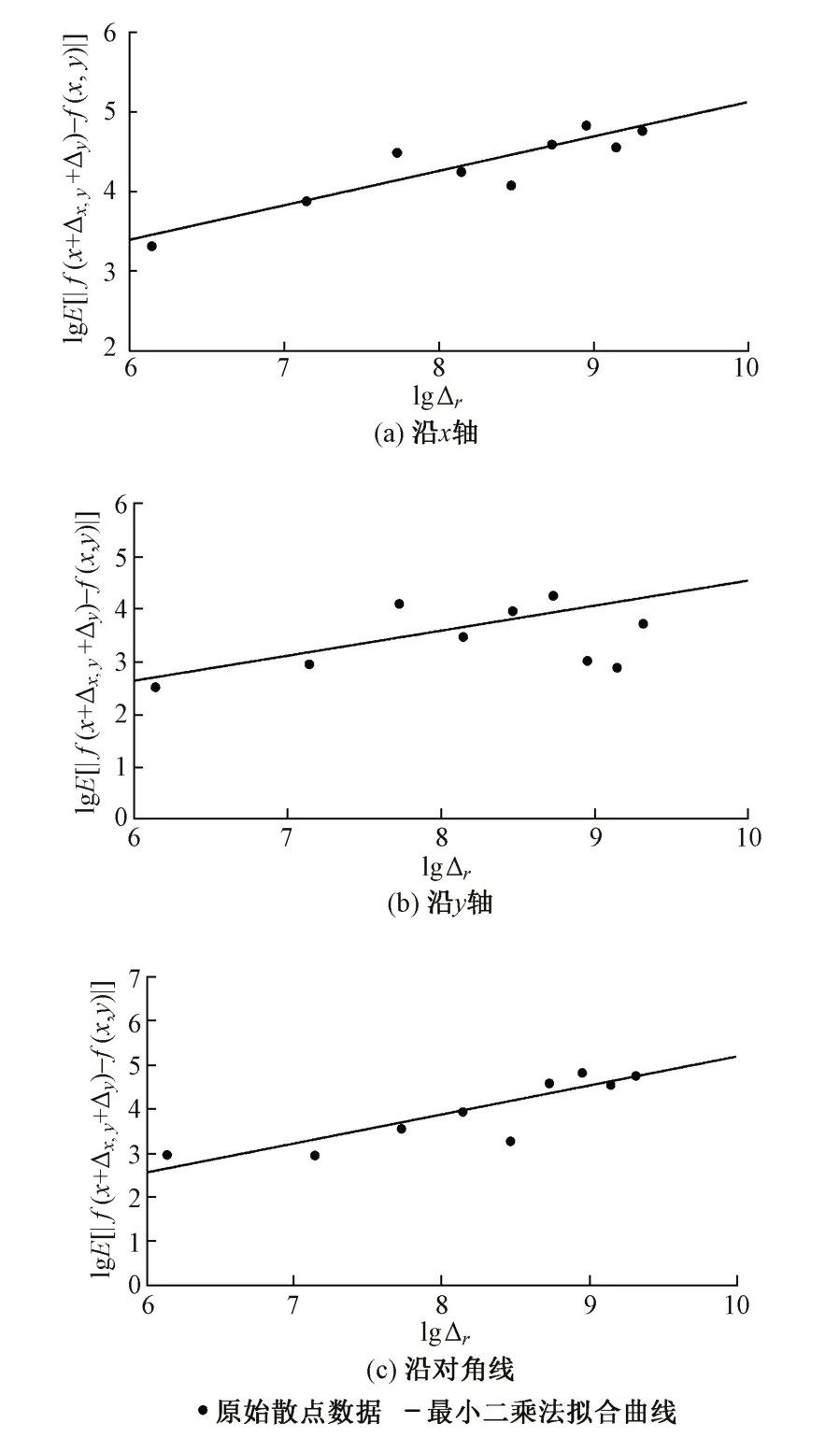
图4 整体数据分形特征拟合
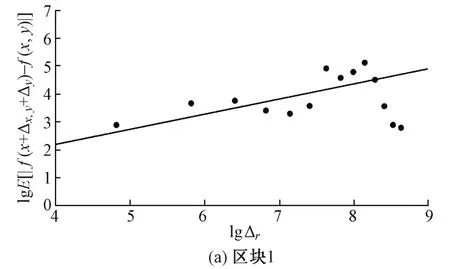
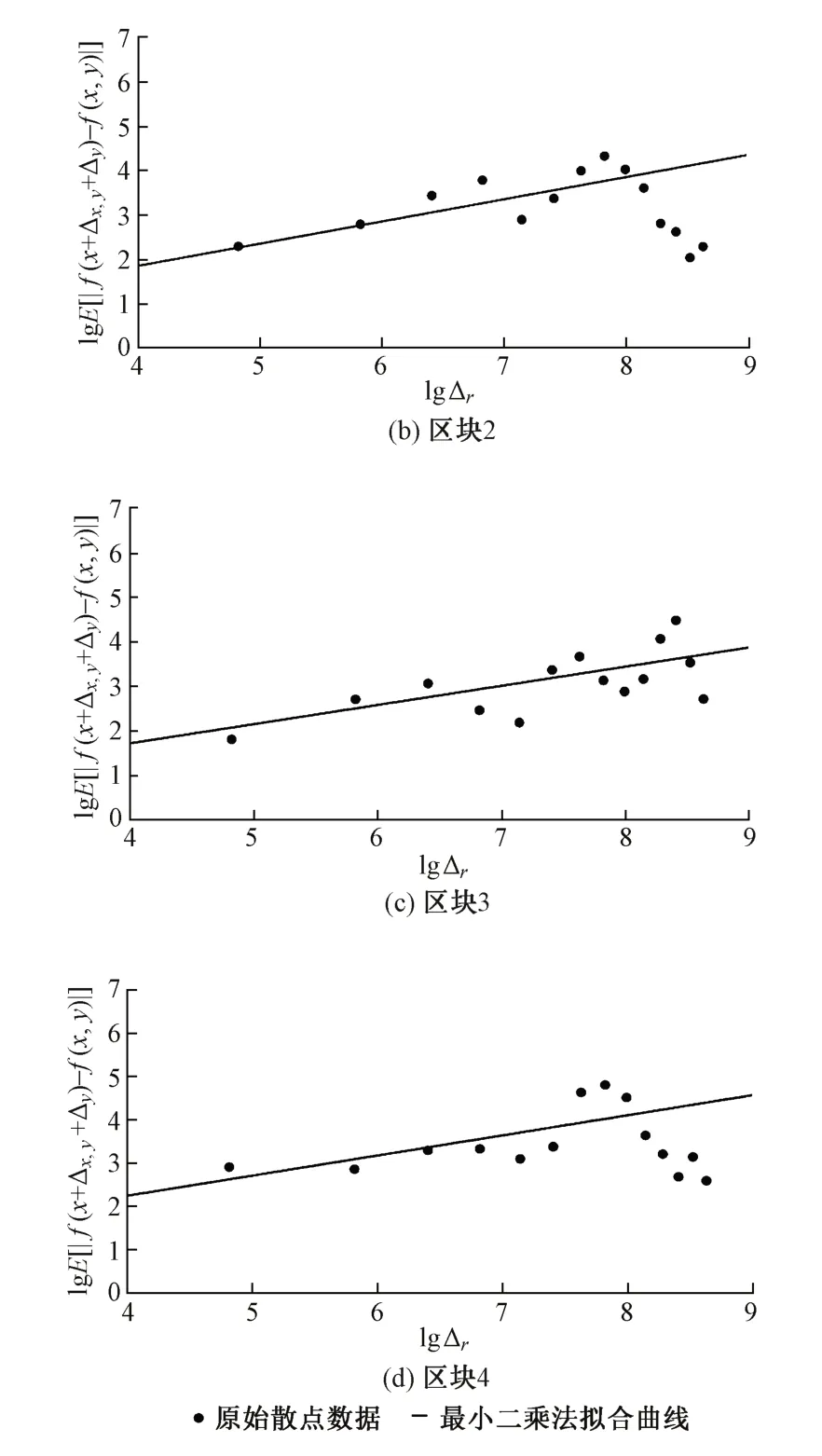
图5 各区块分形特征拟合
由图4(a)可知,沿x轴采样数据整体只呈现一个无标度区,采样点数据分布趋势基本一致,拟合可得该地形沿x轴的分形特征值为H=0.432 8,δ=3.845。
由图4(b)可知,沿y轴采样数据整体只呈现一个无标度区,无错误点,拟合可得该地形沿y轴的分形特征值为H=0.476 5,δ=1.906。
由图4(c)可知,沿对角线采样数据整体只呈现一个无标度区,无错误点,拟合可得该地形沿对角线的分形特征值为H=0.659 1,δ=0.845。
由图5(a)可知,对区块1 进行采样获得的数据以lg Δr=8 为界限呈现两个无标度区,在lg Δr=7.8 后出现另一个无标度区,与区块1 多数数据呈现的特征不符,因此需要剔除后面的采样点,最终拟合可得该区块地形分形特征值为H=0.500 7,δ=1.998。
由图5(b)可知,对区块2 进行采样获得的数据整体呈现一个无标度区,最终拟合可得该区块地形分形特征值为H=0.430 3,δ=2.228。
由图5(c)可知,对区块3 进行采样获得的数据以lg Δr=7.8 为界限呈现两个无标度区,在lg Δr=7.8后出现另一个无标度区,与区块3 多数数据呈现的特征不符,因此拟合时只对第一个无标度区进行拟合,最终拟合可得该区块地形分形特征值为H=0.529 1,δ=1.935。
由图5(d)可知,对区块4 进行采样获得的数据呈现两个无标度区,在lg Δr=8.2 后出现另一个无标度区,与区块4多数数据呈现的特征不符,因此拟合时只对第一个无标度区进行拟合,最终拟合可得该区块地形分形特征值为H=0.543 6,δ=2.202。
对所有的数据结果进行整理,结果见表1。可知,无人机获取的试验区域地形数据,无论采用三个方向对整体数据采样,或者是对数据划分,提取出的分形特征值基本一致,分形维数D始终保持在2.5 左右。因此在进行分形插值构网时,可以采用全局使用一个分形特征值进行插值算法的编译。
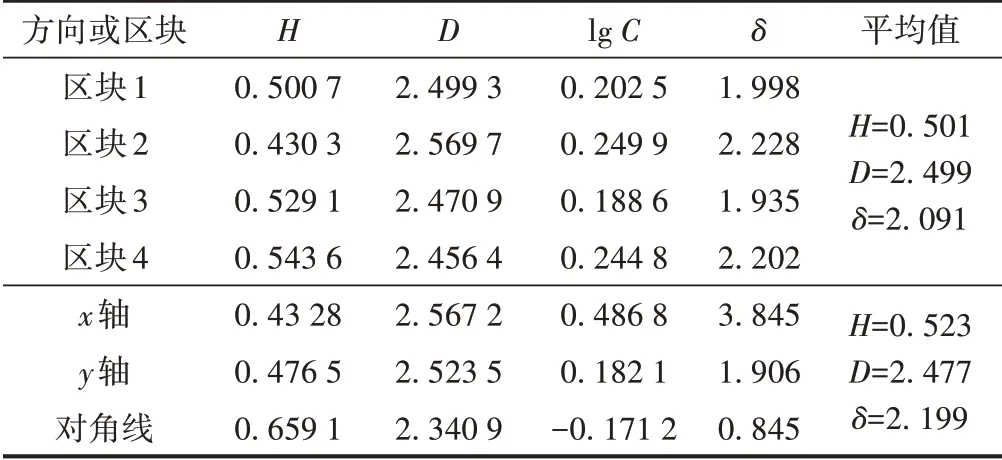
表1 地形分形特征值统计
3.2.3 曲面生成
根据分形布朗运动原理,基于地形数据、重采样数据及拟合出的分形特征值,利用改进随机中点位移法,通过编制分形程序并加载到BIM 软件OpenRail Designer,可实现不同特征值的地形分形模拟。
对同一地形(图6),采用区块分形特征值(H=0.501,δ=2.091)和整体分形特征值(H=0.523,δ=2.199)进行插值构网,迭代一次得到图7(a)和图7(b),视觉上两个地形的表达差异极小。

图6 原始地形
当使用整体分形特征值迭代两次以后,得到的地形[图7(c)]显示效果优秀,已经完全能够表达原地形的起伏特征,从表2的平均坡率也能验证这一点。


图7 三种工况的分形地形

表2 原始地形与分形地形指标对比
由表2 可知:第一次迭代点数为8 320,仅为原始地形点数的0.831%,网格数也仅为原始网格数的0.821%;经第二次迭代,点数与网格数分别是原始数据的2.270%和2.286%。结合对比运算时间,采用分形算法对地形进行轻量化是切实可靠的,可用极少地形控制点完美实现地形特征表达,在节约内存、提高地形构网效率方面也有较大优势。
此方法能更好地解决铁路BIM 与GIS设计过程中长带状地形数据量庞大、加载缓慢的问题。
4 结论
1)通过比较区块与整体分形特征值,无论是采用三个方向对整体数据采样,或是对数据划分,对每个区块采样进行分形特征值的拟合,提取出的分形特征值基本一致,分形维数D始终保持在2.5左右。因此,在进行分形插值构网时,可以采用全局使用一个分形特征值进行插值算法的编译。
2)基于分形算法的地形模型重构可以由极少部分地形控制点较好地表达原地形的特征,并能根据实际需求动态控制地形的细化程度,解决软件构网方式单一化问题,满足工程实际中多式样的地形显示需求,解决了地形轻量化表达问题。
