重载铁路钢轨波磨区段的车辆-轨道动力学特性
2022-02-07王巍林燕玲
王巍 林燕玲
1.国能黄大铁路有限责任公司,山东 东营 257092;2.国能朔黄铁路发展有限责任公司 物流分公司,河北 沧州 062350
随着我国重载铁路的发展,列车轴重不断提高,动荷载作用随之增大,轨面损伤现象频繁发生[1]。据调研,我国朔黄铁路、大秦铁路、神朔铁路等重载线路均存在钢轨波磨,钢轨表面沿线路纵向出现周期性不平顺[2-4]。钢轨波磨多发生于曲线段,列车通过钢轨波磨地段时会产生剧烈的轮轨冲击作用,严重降低了车辆及轨道结构零部件的使用寿命,影响了线路的正常服役状态[5]。因此,研究重载铁路波磨对车辆-轨道动力特性的影响尤为重要。
国内外学者进行了大量相关研究,提出了多种用于解释波磨形成的理论[6-7],如扭转振动理论[8]、轨道共振理论[9]、自激振动理论[10-11],反馈振动理论[12]等。关于钢轨波磨对车辆-轨道动力学特性影响的研究也不断开展。周永健等[13]通过分析实测短波不平顺数据,研究了不同轨面不平顺、不同运行条件下车辆动力响应对运行列车安全性和稳定性的影响。郭涛等[14]选取客运专线高速区段典型的钢轨波磨(波长120~150 mm,波深0.02~0.06 mm)进行研究,发现轮轨垂向力、轴箱振动加速度级、构架振动加速度级随速度增大呈现增大趋势,与波长成反比。王洪刚等[15]研究了地铁曲线地段上车辆运行速度和曲线半径对轮轨磨耗的影响,发现曲线半径对钢轨磨耗功率影响较大,建议在符合城市规划等决定因素要求前提下,地铁线路曲线半径尽量大于500 m,最高运营速度以60~70 km/h 为宜。崔旭浩等[16]考虑道砟颗粒的不规则外形,采用离散单元法建立有砟道床的数值模型,分析了钢轨波磨对重载铁路有砟道床动力特性的影响。
既有研究大多集中于地铁和高速铁路波磨对车辆-轨道动力学特性的影响,关于重载铁路波磨地段的车辆-轨道动力特性的研究较少。本文基于重载铁路实际存在的钢轨波磨状态,以谐波不平顺为线路激扰,研究钢轨波磨特征、曲线半径以及超高状态对车辆-轨道动力特性的影响,为重载铁路曲线参数的优化以及波磨的整治提供理论基础。
1 重载列车-轨道耦合动力学模型
1.1 建立模型
采用SIMPACK 软件建立重载铁路C80货车模型,轴重25 t[17]。转向架为ZK6 型三大件式货车转向架,由轮对、轴箱、八字形橡胶垫、摇枕、侧架、中央两级刚度弹簧悬挂系统及横向摩擦减振装置、集成制动装置组成。ZK6型转向架的轮对和侧架间采用导框与承载鞍橡胶实现弹性定位,橡胶垫相当于给转向架配置了非线性的一系悬挂系统,转向架的簧下质量得以优化,降低了轮轨之间动态相互作用。二系减振系统采用内、外两级刚度的螺旋钢弹簧。此外,为了保证车辆的运动稳定性,转向架加装了交叉支撑装置,增强了转向架抗菱形变形能力。
将车体、摇枕、侧架、轮对简化成刚体。充分考虑货车部件的非线性特性,采用多点-面接触模型模拟部件间的摩擦接触。不考虑货车各部件自身的弹性变形,将车体、侧架、摇枕、轮对简化为具有纵向、横移、沉浮、侧滚、点头及摇头六个自由度的刚体。将减振器考虑成刚体,简化为具有纵向、横移、沉浮三个自由度的刚体。重载列车系统总自由度为90个。
采用SIMPACK 软件提供的子结构建模方法可以快速、高效、方便地建立车辆-轨道系统动力学模型。由于前后转向架都是ZK6 型,结构完全相同,因此将转向架作为子结构。同时,旁承力和心盘力是车体与摇枕之间的作用,为了避免主模型中这些力重复施加,引入虚车体。在ZK6 转向架模型中,前后轮对的参数是完全相同的,因此把轮对模型也作为转向架模型的子结构来处理。
重载列车-轨道动力学模型如图1 所示。轮轨法向接触力采用Hertz 非线性接触理论,轮轨切向接触力的计算采用Kalker 简化非线性理论。线路组成为100 m直线段+100 m缓和曲线段+240 m圆曲线段。
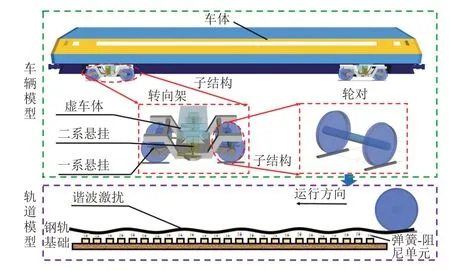
图1 重载列车-轨道耦合动力学模型
1.2 设置线路激扰
列车在实际运行过程中不断受到各种轨道不平顺激扰,为了真实模拟重载列车的实际运行状况,须施加符合线路实际特征的钢轨不平顺。钢轨波磨主要由波长和波深两个表征参数构成,是典型的连续谐波激扰。本模型中对波磨进行模拟时,采用国际上铁路通用的连续周期性余弦函数来描述钢轨波磨现象[2],其表达式为

式中:Z为波磨在钢轨表面的垂向位置;t、n分别为时间变量和激扰波数;L、a分别为不平顺波长和波深;v为车辆运行速度。
2 动力学特性
2.1 波磨特征对车辆-轨道动力学特性的影响
2.1.1 波磨波长
计算工况取直线段,列车运行速度80 km/h,波磨波深取0.3 mm,波磨波长分别取100、150、200、250、300 mm。不同波磨波长下车辆-轨道动力学特性见图2。
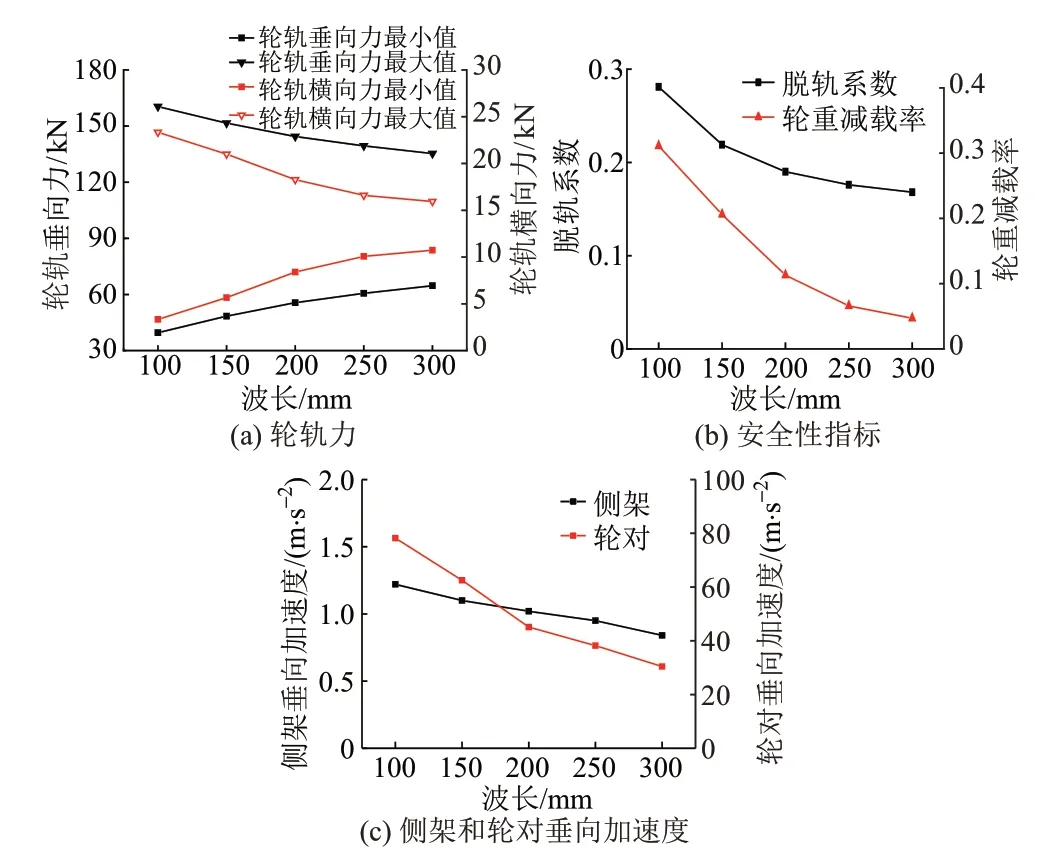
图2 不同波磨波长下车辆-轨道动力学特性
由图2可知:
1)波磨波长从100 mm 增至300 mm,轮轨垂向力和横向力最大值分别减小15.6%、31.7%,最小值分别增大63.4%、222.0%。轮轨垂向力、横向力最大值随波长增大而减小,而最小值随波长增大而增大。可见,波磨波长越小,轮轨力的波动幅值越大。
2)波磨波长从100 mm 增至300 mm,脱轨系数和轮重减载率分别减小40.2%、84.9%。可见,波磨波长越小,对车辆运行安全性越不利。
3)波磨波长从100 mm 增至300 mm,侧架和轮对加速度分别减小31.1%、61.1%。可见,波磨波长越小,对车辆动力学特性影响越大。
2.1.2 波磨波深
计算工况取直线段,列车运行速度80 km/h,波磨波长取200 mm,波磨波深分别取0.1、0.2、0.3、0.4、0.5 mm。不同波磨波深下车辆-轨道动力学特性见图3。
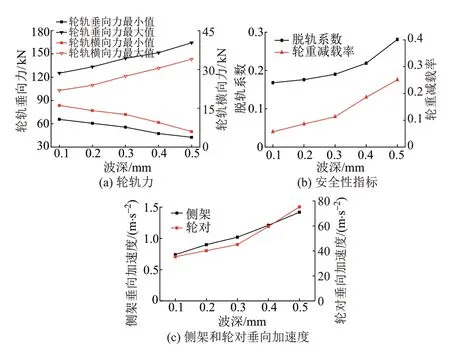
图3 不同波磨波深下车辆-轨道动力学特性
由图3可知:
1)波磨波深从0.1 mm 增至0.5 mm,轮轨垂向力和横向力最大值分别增大了31.2%、55.3%,最小值分别减小了35.2%、62.7%。轮轨垂向力、横向力最大值随波深增大而增大,最小值随波深增大而减小。可见,波磨波深越大,轮轨力的波动幅值越大。
2)波磨波深从0.1 mm 增至0.5 mm,脱轨系数和轮重减载率分别增大67.3%、330.4%。可见,波磨波深越大,对车辆运行安全性越不利。
3)波磨波深从0.1 mm 增至0.5 mm,侧架和轮对加速度分别增大91.9%、112.4%。可见,波磨波深越大,对车辆动力学特性影响越大。
2.2 曲线半径对车辆-轨道动力学特性的影响
计算时,列车运行速度取80 km/h,波磨波长取200 mm,波磨波深取0.3 mm,曲线半径分别取450、550、650、750、850 m,根据GB 50090—2006《铁路线路设计规范》[18],得出曲线超高依次为120、120、115、100、90 mm。不同曲线半径下车辆-轨道动力学特性见图4。可知:
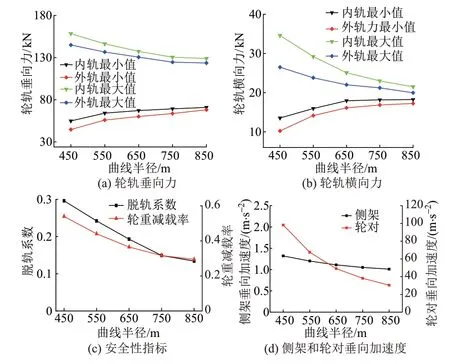
图4 不同曲线半径下车辆-轨道动力学特性
1)轮轨垂向力、横向力最大值随着曲线半径增大而减小,最小值随着曲线半径增大而增大;曲线半径由450 m 增至850 m,内轨的垂向力、横向力最大值分别减小19.3%、35.3%,外轨的垂向力、横向力最小值分别增大9.6%、22.3%。可见,曲线半径对内轨轮轨力影响更大,且轮轨力波动幅值随曲线半径增加而减小。小半径曲线除了存在较大轮轨力外,内外轨受力更加不均匀,导致内轨钢轨波磨更加严重。
2)曲线半径越小,脱轨系数和轮重减载率越大。小半径曲线对重载列车的安全运营存在较大影响,需特别关注。
3)曲线半径由450 m 增至850 m 时,侧架垂向加速度减小23.4%,轮对垂向加速度减小69.9%,曲线半径的变化对轮对垂向加速度的影响更大。可见,存在钢轨波磨的小半径曲线地段对侧架和轮对的振动加速度影响较大,需要特别关注波磨严重的小半径曲线地段。
2.3 曲线超高对车辆-轨道动力学特性的影响
计算时,列车运行速度取80 km/h,波磨波长取200 mm,波磨波深取0.3 mm,曲线半径取750 m。按超高不同设置工况1—工况5 五种工况,依次为:欠超高20 mm、欠超高10 mm、平衡超高、过超高10 mm、过超高20 mm。不同超高工况下车辆-轨道动力学特性见图5。
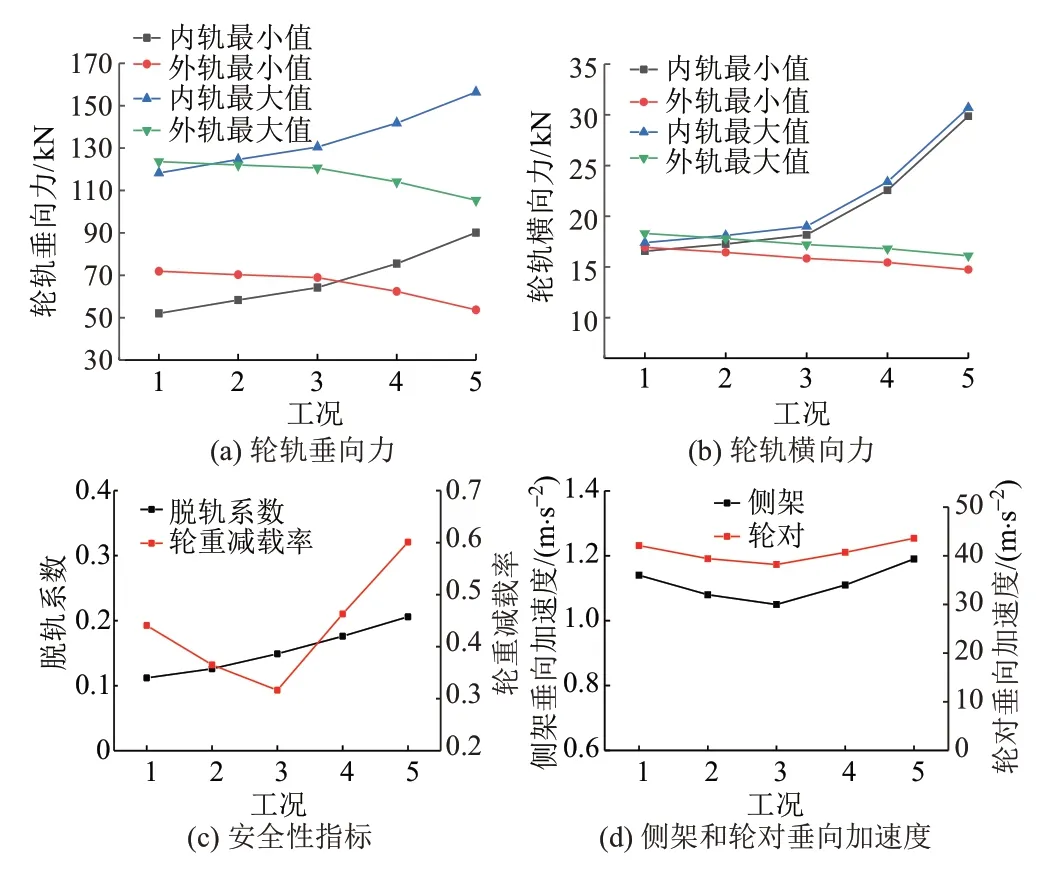
图5 不同超高工况下车辆-轨道动力学特性
由图5可知:
1)从欠超高20 mm 变化到过超高20 mm,内轨垂向力、横向力极值不断增大,而外轨垂向力、横向力极值不断减小。线路处于欠超高状态时,从欠超高20 mm 到欠超高10 mm 再到平衡超高,内轨垂向力最大值分别增大了5.1%、10.2%,外轨垂向力最大值分别减少了1.3%、2.9%,内轨横向力最大值分别增大了4.0%、9.2%,外轨横向力最大值分别减少了2.7%、6.0%;线路处于过超高状态时,从平衡超高到过超高10 mm 再到过超高20 mm,内轨垂向力最大值分别增大了9.1%、20.3%,外轨垂向力最大值分别减少了5.3%、12.5%,内轨横向力最大值分别增大了23.2%、61.58%,外轨横向力最大值分别减少了2.3%、6.4%。可见,在过超高状态下轮轨垂向力、横向力变化幅度更大,这说明车辆-轨道系统对过超高更为敏感。较大的曲线超高导致内轨的轮轨磨耗增大,造成过超高地段较快出现钢轨波磨。
2)从工况1 到工况5,脱轨系数逐渐增大,而轮重减载率呈先减小后增大的趋势。不同超高下的脱轨系数和轮重减载率均小于GB∕T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》[19]规定的限值,但是轮重减载率整体处于较高水平,在钢轨波磨严重地段会影响列车运行安全。
3)从工况1到工况5,侧架和轮对垂向加速度均呈现先减小后增大的趋势,但变化幅度不大,在10%以下。可见,超高状态对侧架和轮对垂向加速度的影响较小。
3 结论
1)钢轨波磨波长越小,波深越大,则轮轨垂向力、横向力波动幅度越大,脱轨系数、轮重减载率、侧架和轮对垂向加速度越大,对车辆-轨道动力学特性的影响越明显。
2)对于半径450~850 m 的曲线区段,轮轨垂向力、横向力最大值随曲线半径增大而减少,最小值随曲线半径增大而增大。曲线半径越小,轮轨垂向力、横向力波动幅度越大,脱轨系数、轮重减载率、侧架和轮对垂向加速度越大。曲线半径的变化对侧架和轮对垂向加速度的影响大;相比外轨,曲线半径的变化对内轨轮轨力影响更大。
3)从欠超高20 mm 到过超高20 mm,内轨垂向力、横向力的极值不断增大,外轨垂向力、横向力的极值不断减小;脱轨系数逐渐增大,轮重减载率先减小后增大。超高状态对侧架和轮对垂向加速度的影响不大。
4)需要格外关注短波长、大波深以及小半径曲线地段的钢轨波磨发展情况。
