多联大跨度钢桁桥上无缝线路设计方案可行性研究
2022-02-07郝晓成米洋
郝晓成 米洋
中铁第六勘察设计院集团有限公司,天津 300308
无缝线路轨道结构由于没有钢轨普通接头,平顺性大幅提高,轨道结构强度和整体性增强,成为现代轨道结构的关键技术之一[1-3]。随着我国轨道设备质量不断提升,既有线轨道无缝化改造成为线路提质增效的重要手段。既有线不可避免地存在多联大跨度钢桁桥,相比普通桥上无缝线路,其梁轨相互作用更为复杂。钢桁桥桥上无缝线路设计方案成为制约既有线轨道无缝化改造的主要因素。
梁轨相互作用是桥上无缝线路设计的关键问题,国内外学者对此进行了大量研究。文献[4-5]通过钢轨轴向平衡微分方程研究了桥上无缝线路的附加力。文献[6-8]针对斜拉桥、悬索桥等不同桥型的桥上无缝线路设计方案进行了研究。既有研究大多针对新建线路桥上无缝线路,而鲜有既有线钢桁桥明桥面桥上无缝线路设计方案的研究。
本文基于一多联大跨度钢桁桥上无缝线路,建立线-桥-墩一体化模型,提出全桥铺设常阻力扣件、连续梁边跨及相邻简支梁铺设小阻力、连续梁边跨铺设零阻力扣件、连续梁边跨铺设单向伸缩调节器、连续梁跨中铺设单向伸缩调节器五种设计方案。通过进行强度和稳定性检算,对比得出桥上无缝线路最优设计方案,以期为铁路钢桁桥上无缝线路设计检算、结构优化提供参考。
1 模型及方案设计
1.1 计算模型
桥上无缝线路计算模型如图1 所示。将钢轨、桥梁离散成有限个梁单元;扣件及道床纵向阻力特征采用非线性弹簧单元来模拟;桥梁下部结构纵向刚度采用线性弹簧单元来模拟。模型中,考虑连续梁两侧各5 跨简支梁范围内的钢轨及扣件单元,以消除边界条件对桥上无缝线路纵向力和位移计算的影响。

图1 线-桥-墩一体化计算模型
模型中,桥梁的纵向位移及制(启)动力是主动作用,通过梁轨间的纵向约束带动长轨条发生纵向位移,在长轨条中产生纵向附加力;同时梁轨间的纵向约束力以相反方向作用在桥梁上,并传递至固定支座上,带动墩台产生纵向位移,使桥梁翼缘的纵向位移发生改变。可见,线、桥、墩是相互作用的耦合系统。通过求解该系统的平衡位置,即可得到钢轨中的纵向力、位移,桥梁纵向位移,墩台纵向力及位移。
1.2 设计参数
1)轨道参数:60 kg/m钢轨;Ⅲ型混凝土轨枕;弹条Ⅴ型扣件及小阻力扣件;钢桥明桥面采用木枕,K型扣件;最高轨温60.9 ℃,最低轨温-22.2 ℃,设计锁定轨温(29 ± 5)℃。
2)温度荷载:有砟轨道钢梁温差取25 ℃;混凝土梁温差取15 ℃;无砟轨道混凝土梁温差取30 ℃。
3)列车设计荷载:既有钢桁桥采用图2 所示的中—活载;轮轨黏着系数取0.164,荷载加载长度不超过400 m;设计轴重为25 t。

图2 中—活载(尺寸单位:m)
4)道床及扣件纵向阻力:对于有砟桥,约束阻力为道床阻力;对于明桥面,约束阻力为扣件阻力。扣件及道床阻力参考TB 10015—2012《铁路无缝线路设计规范》。
1.3 设计方案
该桥梁全长2.883 km,孔跨布置为55 × 32 m简支T 梁+(48+3 × 64+48)m 连续钢桁梁+24 × 32 m 简支T梁,桥梁位于直线及半径1 000 m 的曲线上。为消除边界效应影响,按5 × 32 m+(48+3 × 64+48)m+5 × 32 m进行计算。
为得出多联大跨度钢桁梁桥上无缝线路最优设计方案,对五种方案(图3)的钢轨强度、轨道稳定性和断缝值进行检算。

图3 多联大跨度钢桁梁桥上无缝线路方案设计(单位:m)
方案一:全桥铺设常阻力扣件。
方案二:连续梁边跨及相邻简支梁铺设小阻力扣件,其余地段铺设常阻力扣件方案。
方案三:连续梁边跨铺设零阻力扣件,其余地段铺设常阻力扣件方案。
方案四:连续梁边跨铺设单向伸缩调节器,其余地段铺设常阻力扣件方案。
方案五:连续梁跨中铺设单向伸缩调节器,其余地段铺设常阻力扣件。
2 检算及对比
2.1 全桥铺设常阻力扣件及局部铺设小阻力扣件方案
TB 10015—2012 规定,应减少钢轨伸缩调节器的设置。因此首先对全桥铺设常阻力扣件方案(方案一)及局部铺设小阻力扣件方案(方案二)进行检算。
2.1.1 钢轨伸缩附加力
方案一与方案二的钢轨伸缩附加力计算结果见图4。可知,方案一、方案二的钢轨伸缩附加力最大值分别为691.81、538.01 kN,铺设小阻力扣件后钢轨伸缩附加力明显减小,均出现在连续梁右端的连续钢桁桥与简支梁梁缝处,距左桥台448 m。

图4 方案一与方案二钢轨伸缩附加力
2.1.2 制(启)动力
由钢轨伸缩附加力计算结果可知,最不利荷载位置为连续梁右端。计算制(启)动力时按最不利工况加载,列车从左侧入桥,列车车头在距左端桥台448 m处,荷载作用在288 m 桥跨上。方案一与方案二的制(启)动力计算结果见图5。可知,方案一、方案二的制(启)动力最大值分别为480.16、453.67 kN,采用小阻力扣件后制(启)动力略有减小。
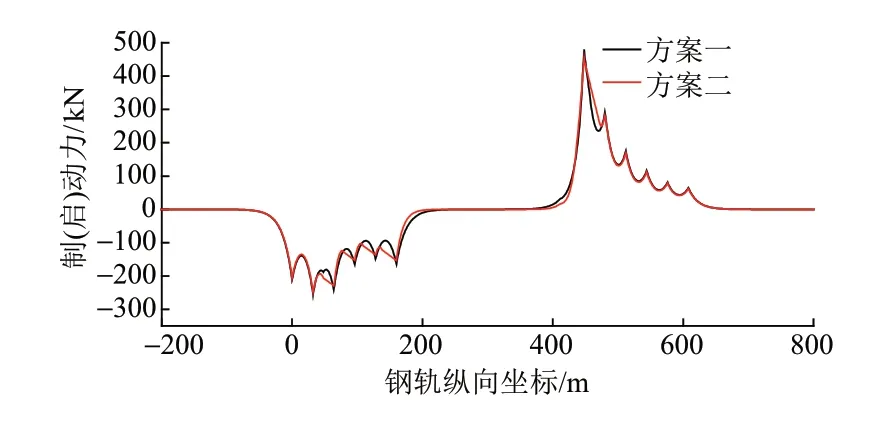
图5 方案一与方案二制(启)动力
2.1.3 断缝值
断缝值的检算关系到行车安全及是否需要采用伸缩调节器,是桥上无缝线路设计的核心内容之一。根据现场经验,桥上无缝线路两股或多股钢轨同时折断的概率极小,因此只考虑单根钢轨折断情况。
考虑最不利工况:钢轨降温56.9 ℃;断缝设置在伸缩力较大的288 m 钢桁梁右端(距左桥台448 m)。方案一与方案二的断缝值计算结果见图6。可知,方案一、方案二的断缝值分别为50.26、69.60 mm。采用小阻力扣件后,由于阻力值变小,断缝值增大,但均小于TB 10015—2012规定的70 mm。

图6 方案一与方案二断缝值
2.1.4 强度和稳定性检算
根据TB 10015—2012,钢轨容许应力为363 MPa。方案一与方案二钢轨强度及无缝线路稳定性检算结果分别见表1、表2。可知,钢轨强度不满足要求,无缝线路稳定性满足要求。这说明铺设常阻力或小阻力扣件钢轨应力较大,方案不可行。
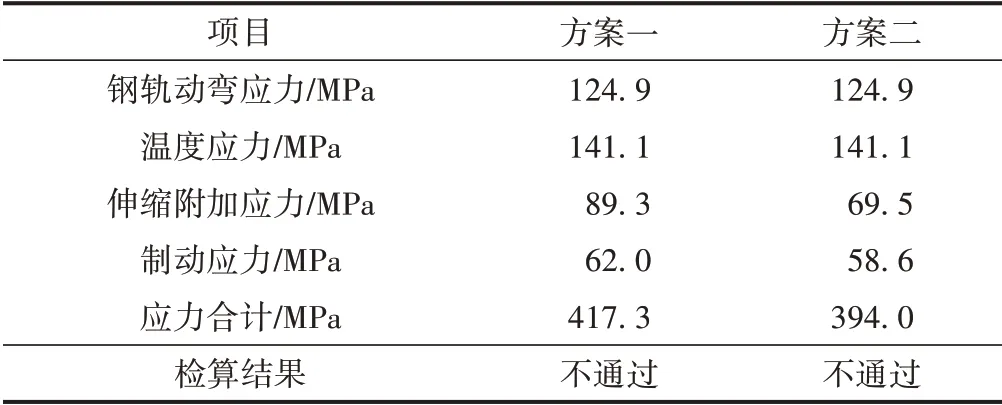
表1 方案一与方案二钢轨强度检算结果
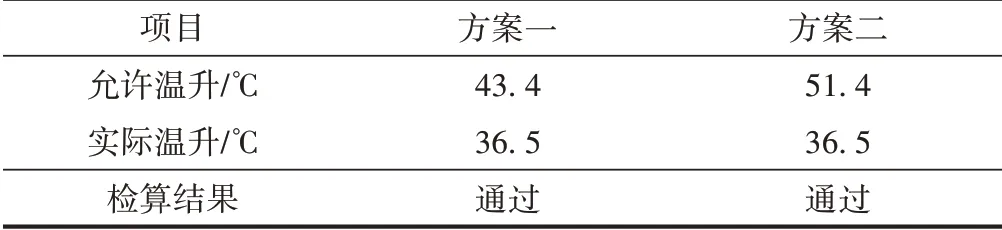
表2 方案一与方案二稳定性检算结果
2.2 连续钢桁梁边跨布设零阻力扣件方案
零阻力扣件,顾名思义就是纵向阻力为0,只有垂向约束作用的扣件[9-10]。基于减少钢轨伸缩调节器设置数量的原则,对连续钢桁梁边跨布设零阻力扣件方案(方案三)进行检算。
2.2.1 钢轨伸缩附加力
方案三的钢轨伸缩附加力计算结果见图7。可知,钢轨伸缩附加力为383.32 kN,出现在连续梁右边跨,明显比方案一、方案二有所减小。
初始阶段。对数据集进行预处理操作,由Job-Client把数据集切片为
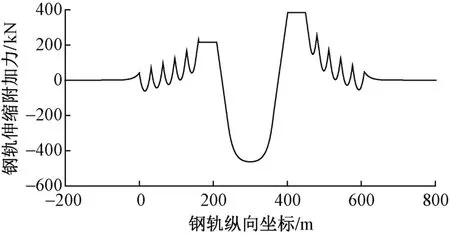
图7 方案三钢轨伸缩附加力
2.2.2 制(启)动力
按照最不利工况加载,列车从左侧入桥,整列车加载到连续梁上。方案三的制(启)动力计算结果见图8。可知,方案三制(启)动力最大值为341.39 kN,明显比方案一、方案二有所减小。
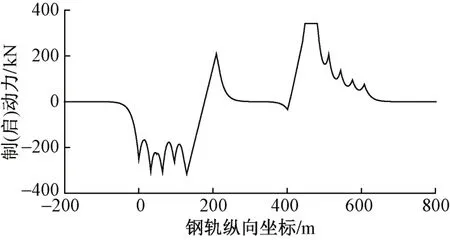
图8 方案三制(启)动力
2.2.3 断缝值
按照最不利工况加载计算方案三断缝值,结果见图9。可知,方案三断缝值为102.27 mm,与方案一、方案二相比明显增大,且大于TB 10015—2012 规定的一般值70 mm、困难值90 mm。
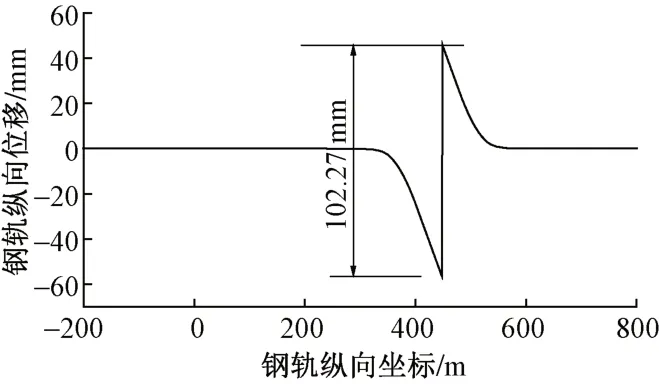
图9 方案三断缝值
2.2.4 强度和稳定性检算
对方案三钢轨强度及无缝线路稳定性进行检算,结果表明:钢轨动弯应力、温度应力、伸缩附加应力、制动应力分别为124.9、141.1、49.5、44.1 MPa,应力合计359.6 MPa,小于容许应力(363 MPa),满足要求;允许温升59.5 ℃,实际温升36.5 ℃,满足要求。
综上,方案三的钢轨强度及无缝线路稳定性均满足要求,但钢轨断缝值不满足要求。方案三不可行。
2.3 铺设伸缩调节器方案
铺设常阻力、小阻力及零阻力扣件方案均不可行,因此需进行连续钢桁梁铺设伸缩调节器方案研究。连续梁铺设伸缩调节器包括边跨铺设(方案四)及跨中铺设(方案五)两种方案。
2.3.1 钢轨伸缩附加力+基本温度力

图10 方案四与方案五钢轨伸缩附加力+基本温度力
2.3.2 制(启)动力
铺设伸缩调节器后,按最不利工况加载时制(启)动力计算结果见图11。可知,方案四、方案五的制(启)动力最大值分别为240.43、480.16 kN。

图11 方案四与方案五制(启)动力
2.3.3 断缝值
铺设伸缩调节器后,考虑断缝出现在最不利工况下,断缝值计算结果见图12。可知,方案四、方案五断缝值分别为48.55、48.56 mm,满足TB 10015—2012限值70 mm的要求。

图12 方案四与方案五断缝值
2.3.4 强度和稳定性检算
方案四与方案五的钢轨强度及无缝线路稳定性检算结果分别见表3、表4。可知,连续梁边跨设置伸缩调节器时,钢轨强度及无缝线路稳定性均满足要求,钢轨断缝值也满足要求;连续梁跨中设置伸缩调节器时,钢轨强度不满足要求。因此,连续梁边跨铺设伸缩调节器方案可行。
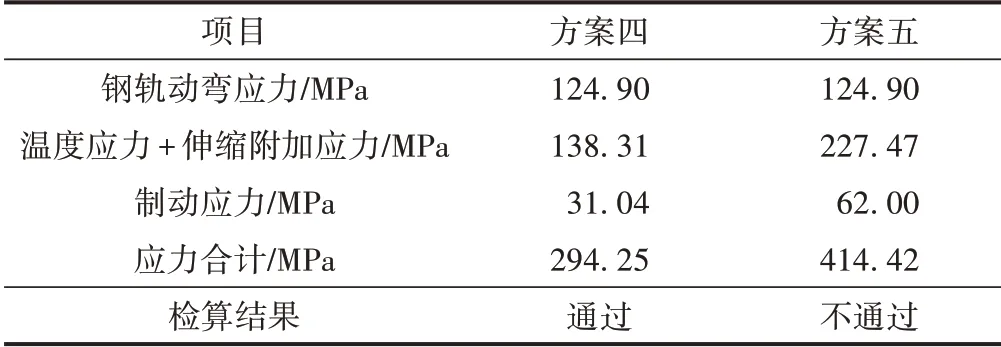
表3 方案四与方案五钢轨强度检算
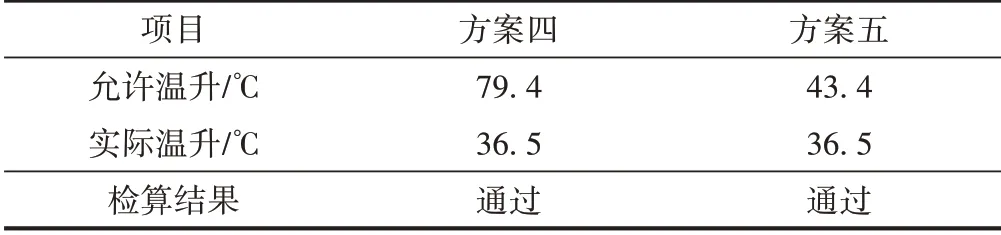
表4 方案四与方案五稳定性检算
3 结论
1)全桥铺设常阻力扣件,钢轨强度不满足要求,无缝线路稳定性满足要求,断缝值满足要求,故方案一不可行。
2)钢桁梁边跨及相邻简支梁铺设小阻力扣件,其余地段铺设常阻力扣件,钢轨强度不满足要求,无缝线路稳定性、断缝值均满足要求,故方案二不可行。
3)钢桁梁边跨铺设零阻力扣件,其余地段铺设小阻力扣件,钢轨强度及无缝线路稳定性均满足要求,但断缝值不满足要求,故方案三不可行。
4)连续梁两端铺设伸缩调节器,钢轨强度及无缝线路稳定性均满足要求,断缝值满足要求,故推荐连续梁两端铺设伸缩调节器方案。
5)连续梁跨中设置伸缩调节器,钢轨强度不满足要求,无缝线路稳定性满足要求,断缝值满足要求,故方案五不可行。
本研究成果可为铁路钢桁桥上无缝线路设计检算、结构优化提供参考。
