弹性机翼刚度的静气弹敏感性研究
2022-02-06陈恺刘晓燕程攀毛昆
陈恺,刘晓燕,程攀,毛昆
上海飞机设计研究院,上海 201210
0 引 言
现代大型民用客机为追求经济性和燃油效率,提高市场竞争力,多遵循高马赫巡航、低结构重量[1]的设计理念,机翼结构多采用复合材料,不可避免地导致了机翼柔度增大[2]、弯曲和扭转变形加剧、机翼载荷分布改变。飞机气动性能降低甚至操纵面出现反效及静气动弹性(简称“静气弹”)效应已经成为影响飞机飞行性能、安全性等指标的重要原因[3-4]。
经过风洞试验验证的在设计巡航点具有最佳气动性能的外形为巡航设计外形;在机翼设计过程中消除机翼静气弹变形影响后形成的用于生产制造的地面外形即为型架外形[5];型架外形在实际高空飞行时承受气动载荷、惯性载荷等作用后成为弹性外形[6]。
进行静气弹评估时,机翼结构刚度是确定机翼结构变形对飞机气动特性影响的重要因素[7]。国内外学者针对大展弦比机翼的刚度设计与静气弹评估开展了研究。Bisplinghof等[8]将机翼简化为沿机翼刚轴方向的悬臂梁,并引入刚度影响系数进行刚度设计;Schuster[9]采用多项式函数模拟刚度曲线,可在已知机翼载荷和扭转分布的情况下反推机翼刚度;刘东岳等[10]提出基于梁架模型气动弹性优化方法和三维优化模型折算方法来进行机翼总体刚度设计;张建刚等[11]耦合工程梁理论和升力面理论来评估机翼弹性对气动载荷的影响。传统方法多采用简化的气动和结构工程模型,静气弹评估精度有所降低。如何耦合高效率、高精度的气动弹性分析方法是评估弹性机翼刚度静气弹影响的一个核心问题。
本文以某大展弦比后掠翼为研究对象,耦合基于 RANS(Reynolds Averaged Navier–Stokes)方程的 CFD(Computation Fluid Dynamics)求解器和结构静力学求解器,发展型架外形设计方法,围绕弹性机翼的刚度开展静气弹敏感性研究,包括分析机翼型架设计的鲁棒性、建立机翼刚度与全机气动导数预测模型以及分析机翼刚度优化敏度。
1 理论方法
1.1 流固耦合方法及型架外形设计方法
本文通过耦合定常Navier–Stokes方程[12]求解器和有限元分析方法,建立流固耦合分析方法,提出基于巡航外形的型架外形设计方法,并基于型架外形开展流固耦合静气弹分析。流体计算采用贴体结构网格,如图1所示。以k–ωSST湍流模型实现流体方程的封闭[13],对流项离散采用二阶迎风格式,并采用多重网格技术加速流场压力分布的收敛。

图1 流体网格Fig.1 Fluid grid
结构分析基于反映结构变形和载荷关系的结构静平衡方程。由于其他部件(包括机身、尾翼、发动机及吊挂)均为刚体部件,虽然发动机、吊挂会随机翼弹性变形产生位移,但与机翼的相对位置始终保持不变,因此本文仅考虑机翼部件的弹性变形。采用如图2所示的鱼骨模型建立结构模型。

图2 结构模型Fig.2 Structural model
结构网格点的位移及气动网格点的气动力数据传递采用无限平板插值方法[14]。为了避免大量网格点移动导致交叉点和网格负体积增多,采用基于非结构背景网格的弹簧网络动网格技术[15]实现流场网格的变形。本文的型架外形修正方法既能反映三维流场的真实流动,也能反映因结构弹性变形导致的机翼展向典型翼型剖面的扭转角分布。型架设计流程如图3所示。
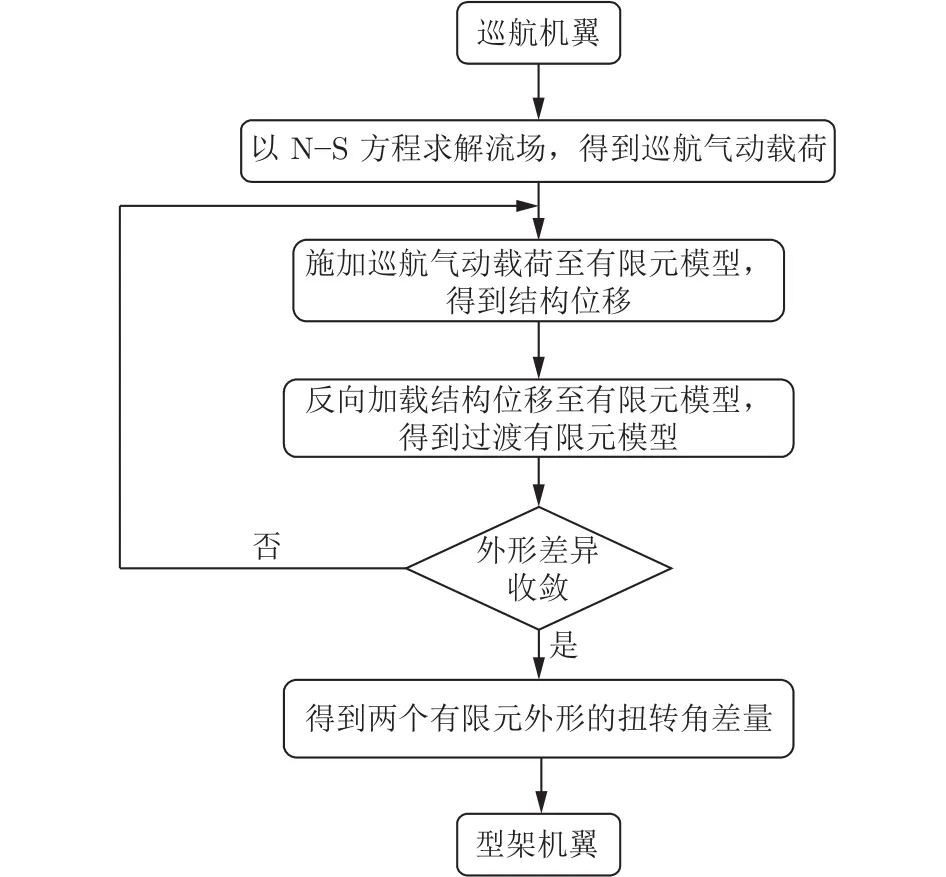
图3 型架外形设计流程Fig.3 Jig shape design process
本文将 CRM(Common Research Model)模型作为验证模型。耦合计算得到的升力系数(CL)、俯仰力矩系数(Cm)与风洞试验结果[16]的对比分别如图4、5所示,图中横坐标为迎角α,升力系数曲线、俯仰力矩系数曲线均与试验结果保持“平行”,验证了本文CFD/CSD方法的精度。
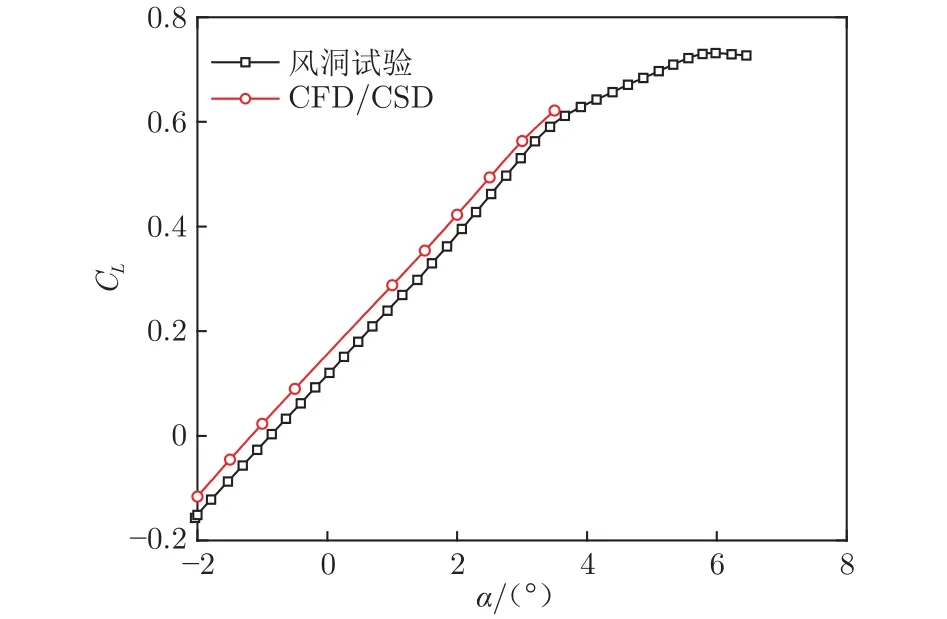
图4 升力系数曲线Fig.4 Lift coefficient curve

图5 俯仰力矩系数曲线Fig.5 Pitch moment coefficient curve
1.2 设计敏度分析方法
在进行优化设计时,获取设计敏度信息可以提高优化效率,减小设计变量定义的不同对优化结果的影响[17-18]。约束函数相对于某设计变量的敏度越大,该设计变量的变化对函数的影响越大,则该设计变量的重要程度越高。同一函数相对于不同设计变量的重要程度是不同的;对于不同的函数,同一设计变量的重要程度也是不一样的。设计敏度的重要性评估公式[19]为:
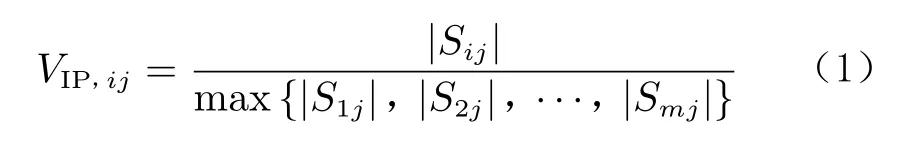
式中,VIP,ij为第i个设计变量相对于第j个函数的重要性, Sij为第j个函数相对于第i个设计变量的设计敏度,m为设计变量的个数。单个设计变量的敏度系数在整体敏度中所占的百分比贡献计算公式为:
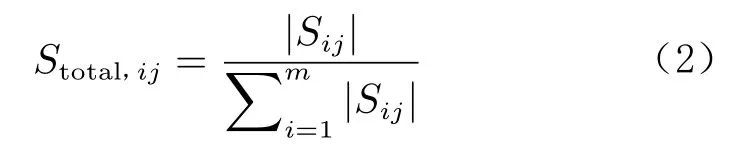
一组同类型的设计变量敏度系数在整体敏度中所占的百分比贡献计算公式为:
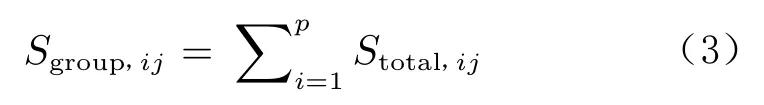
式中,p为同类型设计变量个数。
本文选取机翼肋站位的刚心点的梁特性作为设计变量,包括垂直弯曲刚度、面内弯曲刚度和扭转刚度,约束选取翼尖扭转角及升力效率,利用Nastran软件开展静气弹约束的设计变量敏度分析。
2 刚度对机翼型架外形设计的敏感性分析
在飞机详细设计阶段的中后期,巡航设计机翼外形冻结,但机翼的刚度特性仍然处于多轮迭代中。为了缩短研制周期,冻结型架外形具有重要的实际工程意义。
以大展弦比跨声速后掠翼为研究对象,改变机翼刚度,刚度比分别为 0.8、0.9、1.0、1.1、1.2。将刚度比为1.0时的设计型架外形定义为冻结型架外形,在其他刚度比下根据新刚度特性更新有限元模型。比较分别从新设计型架外形、冻结型架外形出发,经过流固耦合计算变形得到弹性外形的扭转角差量,搜索冻结型架外形的临界刚度比。
巡航马赫数为0.84,采用定升力计算以保持飞机始终处于相同飞行状态下,巡航升力系数为0.49。图6为不同刚度比下是否进行型架外形设计的弹性机翼扭转角差量( Δθ)展向分布对比,其中 Δθ的表达式为:
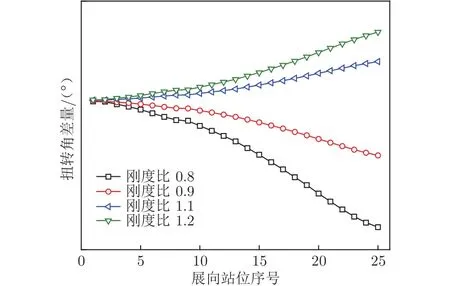
图6 弹性机翼的扭转角差量Fig.6 Delta twist angle of elastic wing along wing span

式中,θUnjig为从冻结型架外形出发得到的弹性机翼扭转角,θJig为从新设计型架外形出发得到的弹性机翼扭转角,θCruise为巡航设计外形的扭转角。
图7为弹性机翼的翼尖扭转角差量与刚度比的关系。 Δθ与刚度比并非线性关系,刚度的增大和减小对扭转角的影响并不对称,减小刚度对扭转角的影响更为显著。机翼刚度变化越大,|Δθ|越大,且机翼刚度减小比刚度增大导致的扭转角变化更为明显,更新型架外形尤为必要。当刚度增大且刚度比不高于1.1时,扭转角误差低于风洞试验测量的角度误差,这意味着精度在工程设计可接受范围内。

图7 弹性机翼的翼尖扭转角差量与刚度比的关系Fig.7 Relationship between delta wing-tip twist angle and stiffness ratio
图8为不同刚度比(1.1、1.2)下,3种机翼构型在展向85%站位处的压力分布对比。图中,Cruise为巡航设计外形,Unjig为从冻结型架外形出发变形得到的弹性外形,Jig为从新设计型架外形出发变形得到的弹性外形,纵坐标为压力系数Cp,横坐标为弦向相对位置x/c。图中刚度比为1.1时,3条曲线重合度较高,压力分布差异不大,但刚度比增大到1.2时,Unjig在压力面靠近前缘处与另外两条曲线有一定差异,且Unjig的激波弦向位置更接近后缘,Jig的压力分布更接近Cruise。

图8 压力分布对比Fig.8 Comparison of pressure distribution
刚度比不同时,是否进行型架修正,巡航点处全机气动力系数差异有所不同。刚度比为1.1时,同升力时巡航迎角差量≤0.1°,阻力差量≤0.000 1,翼根弯矩差量≤1%;但刚度比为1.2时,全机气动特性对型架外形较为敏感,巡航迎角、阻力特性及载荷特性差异明显增大。
综合考虑扭转角分布、压力分布及全机气动特性,在飞机工程设计的后期,当机翼结构刚度变化≤10%时,为了节省资源、缩短研制周期,可从工程设计角度出发冻结型架外形,评估刚度变化引起的弹性影响。
3 基于机翼刚度的全机弹性气动特性模型
根据第2节的结论,在刚度变化≤10%时,为简化设计流程,节约资源成本,采用冻结外形。刚度变化>10%时,利用更新刚度的有限元模型重新进行型架外形设计,并通过流固耦合方法得到弹性外形,建立机翼刚度比(1.04、1.08、1.10、1.20)与全机气动特性的函数关系,并采用刚度比为1.06的算例检验预测模型的准确度。
将刚度比为1.00的气动导数作为基准值,建立全机升力系数曲线斜率、全机俯仰力矩系数曲线斜率的差量百分比与刚度比之间的关系,分别如图9、10所示。由图可见,升力系数曲线斜率及全机俯仰力矩系数曲线斜率与刚度比均呈现良好的线性关系。
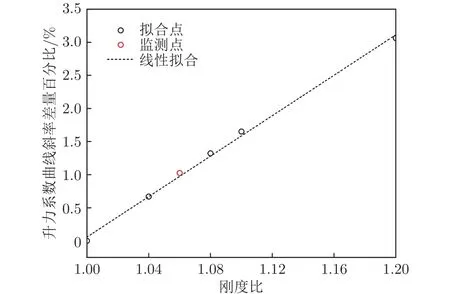
图9 升力系数曲线斜率与刚度比的关系Fig.9 Relationship between slope of lift curve and stiffness
升力系数曲线斜率差量百分比与刚度比的函数模型如式(5)所示:

式中,CL,α为升力系数曲线斜率,k为刚度比。俯仰力矩系数曲线斜率差量百分比与刚度比的函数模型如式(6)所示:

式中,Cm,α为俯仰力矩系数曲线斜率。
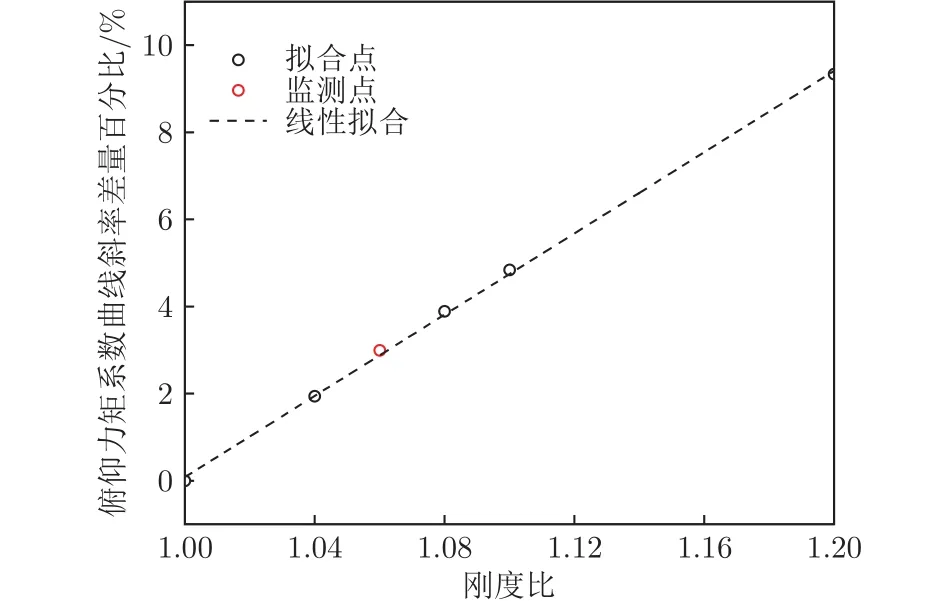
图10 俯仰力矩系数曲线斜率与刚度比的关系Fig.10 Relationship between slope of pitching moment curve and stiffness
当刚度比为1.06时,流固耦合方法所得的弹性气动导数与函数模型预测的结果吻合较好。当机翼刚度频繁迭代时,可以基于此线性工程模型,快速评估弹性气动导数与刚度比之间的关系,无需重新建立耦合模型进行仿真模拟。
4 机翼刚度敏度分析
垂直弯曲刚度、面内弯曲刚度及扭转刚度在扭转角、升力效率约束中的分布分别如图11、12所示。升力效率为弹性升力系数曲线斜率与刚性升力系数曲线斜率的比值。由图可见,垂直弯曲刚度、扭转刚度是影响此两种约束的主要设计变量。
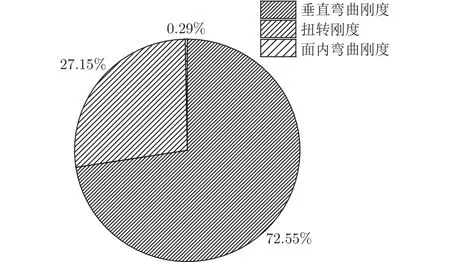
图11 刚度特性在扭转角约束中的分布Fig.11 Distribution of stiffness characteristics under the constraint of twist angle
垂直弯曲刚度对扭转角、升力效率的设计敏度重要性分别如图13、14所示,横坐标表示垂直弯曲刚度设计变量,编号排序从小到大表示从翼根到翼尖的梁展向站位,翼尖站位的垂直弯曲刚度对扭转角影响较为显著,翼根站位的垂直弯曲刚度对升力效率影响较大。扭转刚度对扭转角、升力效率的设计敏度重要性如图15、16所示,扭转刚度对扭转角的影响明显集中在翼尖站位,而翼根站位的扭转刚度对升力效率影响显著。

图12 刚度特性在升力效率约束中的分布Fig.12 Distribution of stiffness characteristics under the constraint of lift efficiency
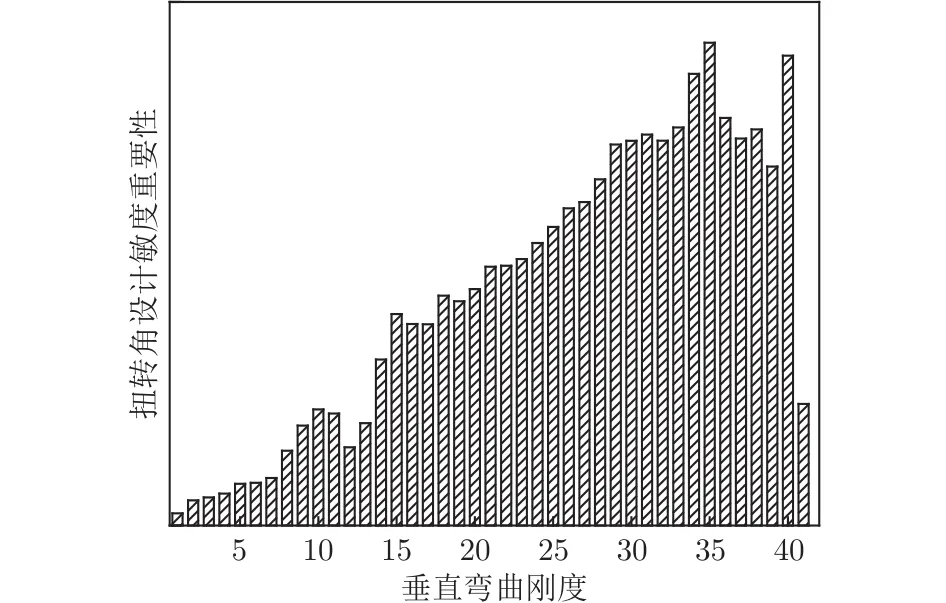
图13 垂直弯曲刚度对扭转角的设计敏度重要性Fig.13 Design sensitivity importance of vertical bending stiffness to twist angle

图14 垂直弯曲刚度对升力效率的设计敏度重要性Fig.14 Design sensitivity importance of vertical bending stiffness to lift efficiency
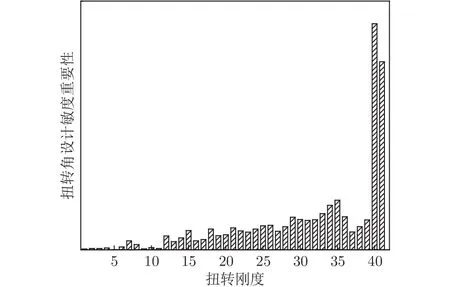
图15 扭转刚度对扭转角的设计敏度重要性Fig.15 Design sensitivity importance of torsional stiffness to twist angle
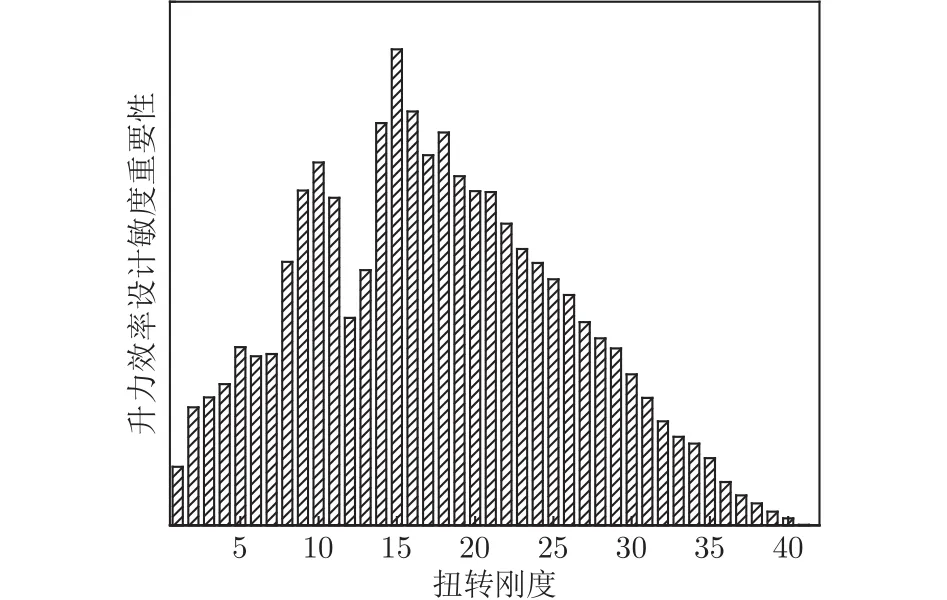
图16 扭转刚度对升力效率的设计敏度重要性Fig.16 Design sensitivity importance of torsional stiffness to lift efficiency
通过敏度分析,可以搜索展向各站位分区的刚度特性对机翼静气弹效应的影响程度,为机翼刚度设计缩小优化范围,提供局部优化方向,以控制气动升力面的静态弹性变形,提高优化设计效率。
5 结 论
本文发展了流固耦合分析及型架外形设计方法,针对某大型客机弹性机翼开展刚度静气弹敏感性研究,可为型号设计中的静气弹快速评估提供工程支持,主要结论如下:
1)综合考虑扭角分布、压力分布及全机气动特性,当机翼结构刚度变化≤10%时,可冻结型架外形,缩短研制周期。
2)全机升力系数曲线斜率、全机俯仰力矩系数曲线斜率与刚度比呈线性关系,基于此规律建立工程快速预测模型,当仅更新刚度值时,可快速评估弹性气动导数。
3)垂直弯曲刚度、扭转刚度是影响扭转角及升力效率的主要设计变量,翼尖站位的垂直弯曲刚度及扭转刚度对扭转角的影响明显,翼根站位的垂直弯曲刚度及扭转刚度对升力效率影响明显。
