台风影响下沿海城市风雨复合灾害风险研究*——以海口市为例

刘 青,王 军,许瀚卿,牛怡莹，魏旭辰

(1.华东师范大学 地理信息科学教育部重点实验室，上海 200241；2.华东师范大学 地理科学学院，上海 200241；3.华东师范大学 上海城市公共安全研究中心，上海 200241)

近年来，“低概率、高致灾”台风灾害事件的发生，引起国际社会的广泛关注，极端事件以及多致灾因子的复合作用成为当前国内外水文气象灾害的研究热点[1-6]。已有学者通过研究大风和降雨二者的联合致灾性来评估台风灾害风险[7-8]。徐明等通过建立日降水量区域极值、极大风速区域极值边缘分布函数，构建台风风雨影响强度联合分布模型，评估了台风“海葵”对上海造成的灾害风险[9]。目前已开展的双变量联合概率研究中，Copula函数是一种应用极广的方法[10-15]。王修勇等以台风最大10 min平均风速和最大小时降水量为统计样本，利用Copula函数研究了台风风雨联合分布关系[16]。侯静惟等采用多种Copula函数计算了海南热带气旋过程最大3 s极值风速和总降水量之间的联合概率[8]。陈立华等选取了125场台风的最大风速、时段降水和累积降水，利用Copula函数构建了符合钦州市的风雨联合概率分布模型[17]。上述研究表明Copula函数作为一种可以研究双变量相关性的方法，在台风风雨联合研究中发挥了重要作用。然而，上述研究多以台风期间的最大风速作为统计样本，此类样本存在一定高估，研究结果往往会放大风速在风雨复合灾害的影响，从而无法真实反映研究区的台风风雨复合灾害特征。

已有研究表明，台风过程极大风速较过程最大风速对台风灾害影响研究更具有指导意义[18]，故本文以海南省海口市为例，选取1960—2017年影响海口市的66场台风，以台风影响过程中的极大风速和累积降雨量为研究样本，利用Mann-Kendall统计检验法分析了台风影响下海口市极大风速和累积降雨的变化特征。根据极值理论拟合并挑选出极大风速和累积降雨的最优边缘分布，基于Copula函数构建台风影响下海口市风雨联合概率分布模型，该模型能够在已知台风过程极大风速的条件下预估降雨的形势，在此基础上，可进一步评估台风影响下海口市风雨复合灾害风险，这对研究区有效应对和防范极端台风风雨复合灾害具有重要的实践意义。

1 研究材料

1.1 研究区概况

海口市位于海南省北部沿海，北邻琼州海峡，与雷州半岛隔海相望，受其特殊的地理位置影响，每逢夏秋两季，海口市极易受到台风的干扰和侵袭，作为中国重要的沿海港口城市之一，海口市所面临的台风风雨复合灾害风险备受关注[19]。有研究统计发现，海口市孕灾环境十分敏感，属于台风高致灾危险区，综合危险性很高[20]。大风和降雨是台风灾害的两个主要致灾因子，台风经过时的大风能够在沿岸掀起大浪大潮，直接威胁到沿海居民的生命安全，同时，台风气流中所蕴藏的大量湿热水汽，在过境时能带来高强度降雨，二者叠加，将促使河流下泄不通，加剧沿海城内涝灾害，严重影响城市的可持续发展[21-22]。据统计，台风“威马逊”(2014年第9号台风)经过海口市时的最大风速达71.5 m/s，期间，海口市发生了严重的暴雨灾害，48 h累积降雨达509.2 mm，该次台风灾害共导致了8人死亡、近89.4亿人民币的经济损失[23]。台风期间海口市大风和降雨的联合致灾性已表明，风雨密切相关。本文利用Copula函数分析台风影响下的极大风速和累积降雨边缘分布特征和联合概率分布特征，对提高海口市防台防涝能力具有一定的指导作用。

1.2 数据来源

本研究所用的台风路径数据由中国气象局上海台风研究所提供，该数据每3 h记录一次，涵盖了1949—2021年西北太平洋(包含南海)海域的台风路径信息，包括台风位置(经、纬度)、2 min平均最大持续风速(m/s)和台风中心附近最低气压(hPa)。按照台风风速大小分为以下6个等级：热带低压、热带风暴、强热带风暴、台风、强台风和超强台风。1960—2017年海口市日尺度降雨数据下载自中国气象局网站(http://data.cma.cn/)，该数据为海口市雨量站记录数据。已有研究表明[24-25]，台风路径经过区域(18°～22°N，109°～113°E)，并且在区域中持续时间超过24 h，能够对海口市产生严重影响，故本研究据此选取了1960—2017年对海口市的产生较大影响的66场典型台风作为研究对象[26]，并统计台风经过海口市的极大风速(即台风路径距离海口市最近时的极大风速)和台风影响过程中的日累积降雨量(即统计台风经过海口市当天和前后一天的累积降雨量[27-28])作为统计样本，以开展台风影响下海口市风雨复合灾害风险研究。

2 研究方法

2.1 台风特征分析

采用Mann-Kendall统计检验法(简称M-K法)分析台风影响过程中极大风速和累积降雨特征。M-K法是一种基于时间序列来统计样本相关性的非参数趋势检验方法，能够有效分析某一自然过程的变化趋势[29]，特别是对于非正态分布的水文数据，该方法具有较高的适用性。利用M-K法对样本进行趋势检验可以得到统计量Z值，若Z值大于0，则样本表现为上升趋势，Z值小于0，则表现为下降趋势，根据95%置信水平来判断样本变化趋势是否显著[30]。结合M-K突变检验法可检验长时间序列中样本是否发生时间突变，可由统计量UK和UB的交点所体现[29,31]。

2.2 边缘分布函数

根据极值理论来拟合台风影响过程中极大风速和累积降雨的边缘分布函数。极值理论通过比较一组数据与该组数据概率分布中值从而获得极值，被广泛的运用于水文气象灾害极值分布研究中[32]。服从极值分布的随机变量往往具有低概率发生、高致灾影响的特征，因此，判断相关随机事件是否服从极值分布是目前开展水文气象灾害研究必不可少的一项工作。极值理论中有多种分布函数，主要包括Weibull、广义极值和Gumbel等分布函数[33]。通过选取最优边缘分布函数拟合极大风速和累积降雨，以此进一步分析台风影响下极大风速和累积降雨的边缘分布特征，为构建台风风雨联合概率分布模型奠定基础。

2.3 二元Copula函数

当两个或多个随机变量具有独立分布时，Copula函数可以用于计算这两个或多个随机变量的联合分布，该理论的应用基于Sklar定理得以实现。定理提出[34]，对于N个随机变量的联合分布，可以将其分解为这N个随机变量各自的边缘分布和一个Copula函数，从而将N个随机变量的随机性和连接性分开。随机变量所服从的边缘分布函数可以对其随机性进行描述，而Copula函数则可以对随机变量的连接性进行描述。目前，Copula函数通常被应用于某一灾害的多个致灾因子同时发生的风险概率估计，特别是暴雨洪涝等水文气象灾害的复合概率计算[35]。常用的二元Copula函数有Gumbel、Clayton和Frank Copula，其表达形式如表1所示。

表1 常用二维Copula函数表达式及参数范围

2.4 统计检验方法

Copula函数模型的检验和评价包括边缘分布模型检验和Copula函数的拟合优度评价。其中边缘分布检验主要看所选分布模型能否很好地拟合变量的实际分布，这是构造Copula函数的关键。Kolmogorov-Smirnov检验法(简称K-S法)是Copula函数参数估计中使用最为广泛的方法，其用于估计变量的边际分布参数。利用K-S法检验边缘分布函数的拟合优度的返回值(Max-Likelihood)越大，表明该分布拟合边缘分布越好。此外，通过计算赤池信息准则(Akaike Information Criteria，AIC)和贝叶斯信息准则(Bayesian Information Criteria，BIC)统计量，也可进一步对Copula函数的拟合优度进行评估[36]，AIC和BIC的值越小，则表明拟合效果越好。

3 结果与讨论

3.1 台风影响下极大风速和累积降雨变化特征分析

利用M-K法对1960—2017年每年影响海口市的总台风数量(TTC)和年台风影响下降雨累积大于25 mm的台风数量(RTC)的变化趋势进行检验分析，结果如图1所示，计算得到TTC变化统计量Z值为-1.142，RTC变化统计量Z值为-0.256，均呈现出不显著下降趋势。为定量分析影响海口市的66场台风事件的过程极大风速和累积降雨量的时间序列变化特征以及是否发生时间突变，本文选择台风年极大风速和年累积降雨量为目标进行M-K趋势和突变检验。M-K突变图中的UF和UB统计量是否存在交点可以判断检验量在长时间序列中是否发生时间突变，交点即为突变开始时间。检验结果如图2和图3所示，极大风速统计量Z值为-1.328，整体呈不显著下降趋势，值得注意的是，年极大风速在1972年发生了突变，1960—1972年呈上升趋势，1972—2017年呈下降趋势。年累积降雨变化统计量Z值为-0.221，表明降雨量随时间变化呈不显著下降趋势，由于在时间序列始末两处交点所分割出的两段时间序列较短不具有代表性，因此本文认为年累积降雨量在1960—2017年没有发生突变。

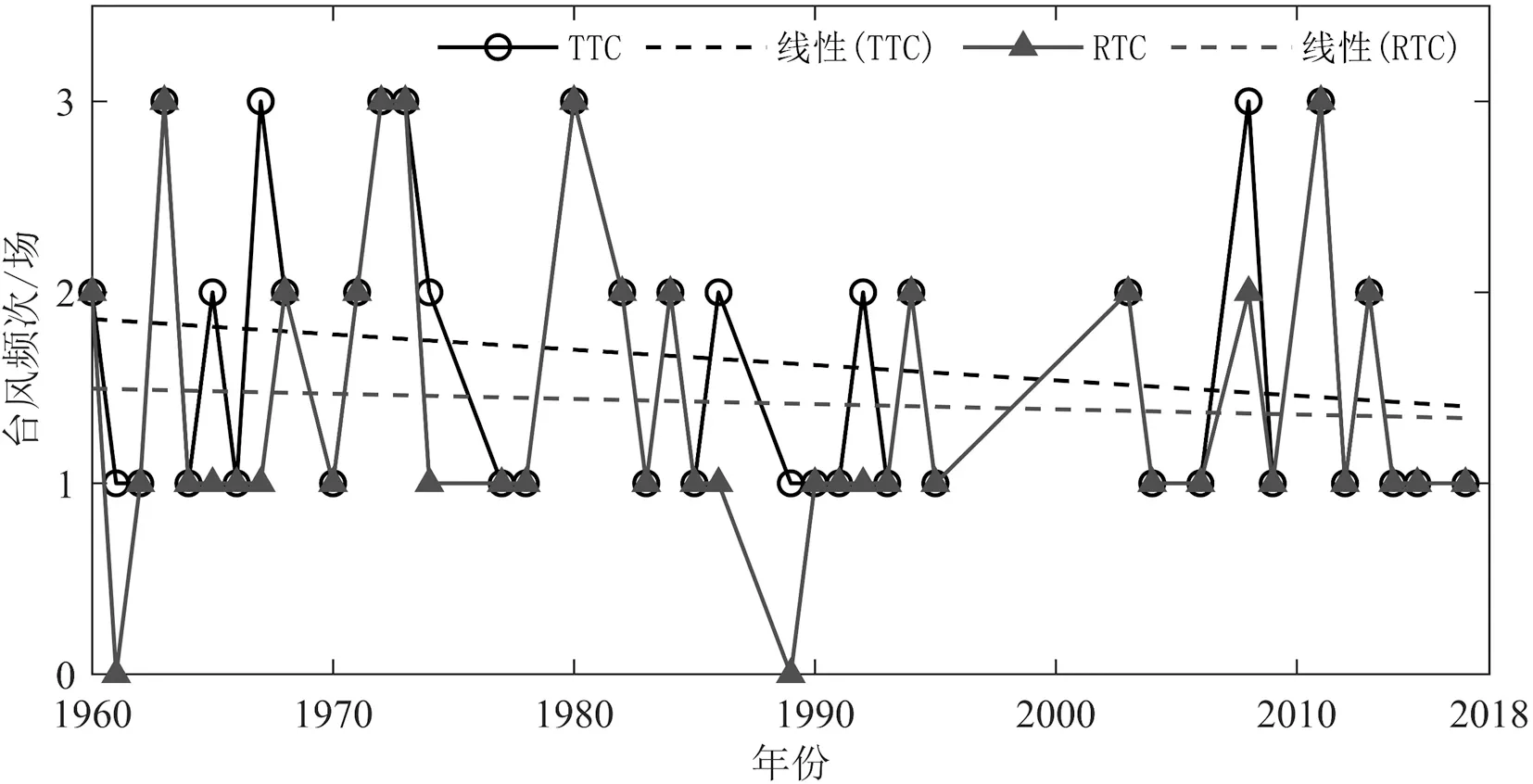
图1 TTC和RTC年际变化

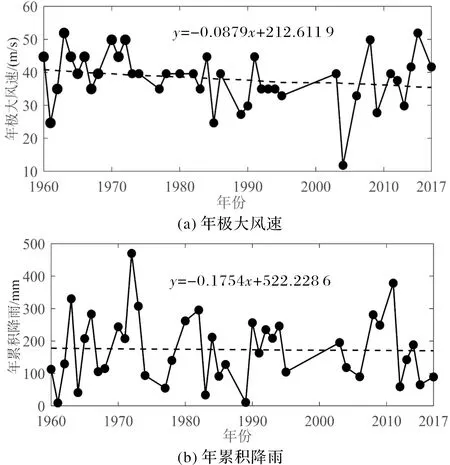
图2 1960—2017年海口市台风影响下年极大风速与年累积降雨趋势分析

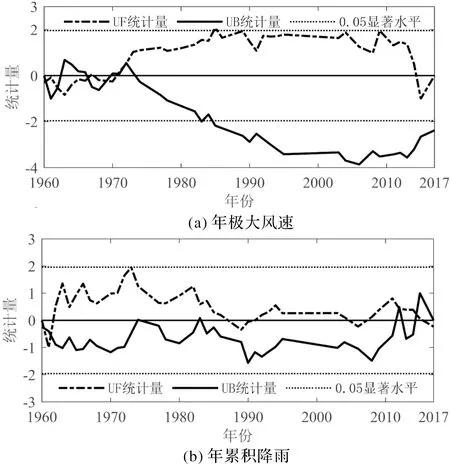
图3 1960—2017年海口市台风影响下年极大风速与年累积降雨M-K突变检验

本文所选取的1960—2017的台风样本的影响强度比较大，结合图2及图3可知，平均每年发生1～2次，且经过海口市时年极大风速基本在20 m/s以上，且大多在40 m/s左右，年累积降雨量主要在200 mm上下波动。1960—2017年海口市TTC、RTC、年极大风速和年累积降雨均呈现出不显著下降趋势，表明未来“低概率，高致灾”台风事件仍有可能增加，出现年极端台风事件下降，风雨强度增大的极端情况，这与目前已有的研究发现一致，未来影响中国的台风将呈现出总量减少、强度增大的趋势[37]。

3.2 极大风速和累积降雨边缘分布拟合

本文采用多个边缘分布函数拟合台风影响下海口市极大风速和累积降雨，包括Gumbel分布、指数分布、Weibull分布、Gamma分布、正态分布、皮尔逊III分布、帕累托分布以及Nakagami分布等，通过计算K-S、AIC和BIC来评价各边缘函数的拟合优度，以选出最优边缘分布函数，并结合QQ(Quantile-Quantile)图直观展示边缘分布函数拟合效果(图4)。由图4可见，Nakagami分布函数对于台风影响下的极大风速具有较好的拟合效果，而指数分布则对于累积降雨量具有较好的拟合效果。

3.3 风雨联合概率分布拟合

本文分别采用Gumbel Copula、Clayton Copula和Frank Copula函数推求极大风速和累积降雨的联合分布，通过计算各个Copula函数的参数值，并将拟合后的联合分布与经验分布进行比较，进一步计算各Copula函数的K-S、AIC和BIC值，计算结果如表2所示。通过对比3组Copula函数的各项检验统计量，研究发现Gumbel Copula函数K-S值小于Frank和Clayton Copula函数，表明Gumbel Copula函数能够更贴切地表达台风影响下海口市风雨复合灾害事件联合分布的典型特征，参数值为1.218，K-S、AIC和BIC值分别为260.41、-518.8和-516.6。

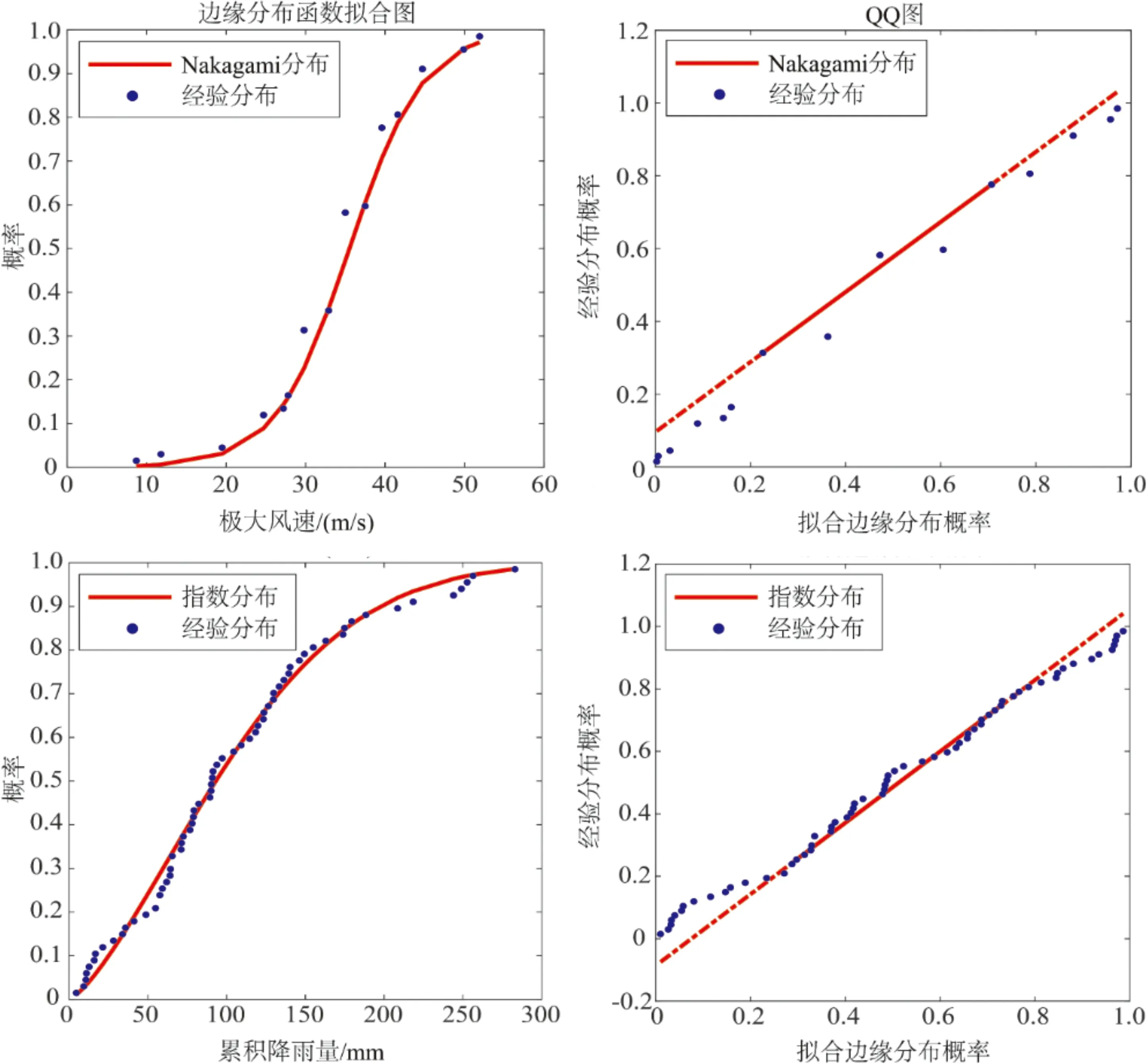
图4 极大风速和累积降雨边缘分布函数

表2 不同Copula联合分布函数拟合优度评价

3.4 风雨联合概率分布模型及应用

根据选定的联合分布函数，本文分别绘制了台风影响过程极大风速和累积降雨的Copula联合累积密度模型和概率密度模型(图5)所示。选择历史影响海口的5场台风事件对该风雨联合概率分布模型进行验证，将5场台风事件影响海口市时的极大风速代入风雨联合概率分布模型中，计算得到相应的累积降雨量(表3)。将实测累积雨量数据与风雨联合概率分布模型模拟的最大可能概率累积降雨量数据范围进行对比，发现这5场台风事件的实测降雨量与模拟数据范围一致，因此该模型能够较为准确和客观地表达台风影响下海口市风雨联合致灾作用。

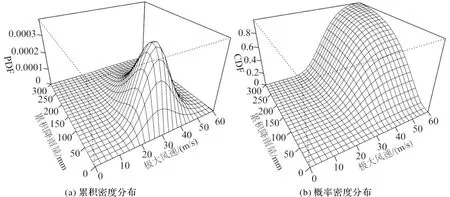
图5 台风影响下海口市风雨联合概率分布模型

表3 台风影响海口期间极大风速、观测累积降雨量和由联合概率分布模型模拟所得降雨量

由于本文所选取的台风事件样本致灾性较强，故该模型可用于反映海口市在极端台风事件影响下风雨复合灾害的风险，即及时根据预报的台风极大风速而推算出海口市可能发生的累积降雨值，从而提前做好应急预案以应对和防范极端风雨复合灾害。此外，基于台风影响下海口市历史最大极值风速，可利用该模型计算出对应的累积降雨值，并根据此估计降雨值进一步设置城市实际防台防涝工程标准，从而降低城市台风风雨复合灾害风险。

4 结论

本研究以海口市为例，基于1960—2017年台风影响下的极大风速与累积降雨量，分别构建了极大风速和累积降雨量的统计样本序列，利用M-K趋势检验法对变化特征进行分析，并根据极值理论优选各序列的边缘分布函数，采用二维Copula函数研究台风影响下风雨联合分布特征和风雨复合灾害风险，得到以下结论：

(1)1960—2017年影响海口市的台风事件特征分析结果显示，TTC、RTC、年极大风速和年累积降雨均呈现出不显著下降趋势，未来“低概率，高致灾”台风事件仍有可能增加，会出现年极端台风事件下降、风雨强度增大的极端情况，应予以关注。

(2)台风影响下海口市极大风速和累积降雨拟合结果显示，Nakagami分布函数对于极大风速具有较好的拟合效果，而指数分布则对于累积降雨具有较好的拟合效果。在多种Copula函数中，Gumbel Copula函数能够较好地描述典型海口市极大风速和累积降雨量(风雨)致灾事件的联合分布。

(3)研究所建立的台风影响下海口市风雨联合概率模型的验证结果显示，该模型能够较准确和客观地表达台风影响下海口市风雨联合致灾作用。未来可利用该联合概率分布模型计算出不同极大风速值所对应的累积降雨值，并根据此估计降雨值进一步设置城市实际防台防涝工程标准，从而降低城市台风风雨复合灾害风险。