剪力墙建筑物在强爆炸作用下的动响应研究

2022-02-04张大民汤文辉王澍霏

现代应用物理 2022年4期

张大民，张昆，汤文辉†, 钟巍, 王澍霏

(1. 国防科技大学文理学院，长沙 410073；2. 西北核技术研究所，西安 710024)

以高层住宅和写字楼为代表的钢筋混凝土(reinforced concrete，RC)剪力墙类建筑在受到强爆炸冲击波作用下，可能在不同区域处发生较复杂的结构破坏，造成重大人员及财产损失。因此，针对这一冲击动力学问题开展数值模拟研究，特别是采用快速算法在第一时刻提供建筑整体的毁伤评估结果具有重要意义。

国内外学者针对这一问题开展了广泛研究[1-5]，具有代表性的数值方法为有限元方法(finite element method，FEM)、单自由度(single degree of freedom，SDOF)方法和多自由度(multiple degree of freedom，SDOF)方法。以LS-DYNA等商业有限元软件为代表的FEM从梁、板等构件层面出发，进行建筑结构建模与单元划分离散，并考虑了RC建筑材料的本构关系，状态方程及复杂边界条件的影响，最终得到丰富细致的计算结果。宋二祥等[6-8]采用LS-DYNA研究了强爆炸作用下某剪力墙建筑顶挠度随载荷强度的变化关系及冲击造成的地下室倾覆问题。FEM的单元数往往在105量级以上，计算较为耗时，虽精度较高，但不满足快速计算的要求。SDOF方法作为一种经典的快速算法[9-10]，将整个剪力墙建筑视为质量集中在楼顶处的悬臂梁结构，对爆炸载荷在建筑冲击面进行等效积分，最终建立并求解一元动力学方程得到建筑顶的挠度。Reyes等[11]开展了结构件的SDOF方法计算并与激波管缩比实验进行了对比，汪维等[12-13]对多种结构采用SDOF方法进行了抗爆性能计算，并利用SDOF方法快速计算特性进行爆炸工况参数扫描计算，得到了结构抗爆P-I曲线。SDOF方法仅有一个自由度，计算效率极高，但对建筑结构过于简化，默认建筑仅发生纯弯曲变形，以建筑顶端的挠度来推测建筑整体的毁伤破坏，难以全面考虑剪力墙建筑的动力学特性，对建筑结构整体采用SDOF方法过于简化了力学模型。MDOF方法可视为SDOF方法的一种优化改进，在保证计算效率同阶的条件下，MDOF方法在建筑结构等效上将每一层建筑进行质量集中等效，并设定为一个自由度，建立了建筑结构整体在横向冲击下主要考虑冲击方向挠度的动力学方程组，进而求解得到以楼层为最小单位的建筑结构动响应，结合给定的损伤判定准则得到建筑整体的破坏情况。El-Dakhakhni等[14]采用上述3种方法开展了RC结构冲击载荷下的数值计算，证明，与SDOF方法相比，MDOF方法计算给出的结构挠度曲线与LS-DYNA更接近。

因此，本文对剪力墙建筑采用多自由度弯剪耦合的方法进行等效建模，用模态分解的方法实现了建筑整体在强爆炸冲击波作用下动响应的快速计算，并通过与有限元计算结果进行比较，对模型进行验证。

1 剪力墙建筑的多自由度弯曲-剪切耦合模型

1.1 模型介绍

基于剪力墙建筑在强爆炸作用下的力学响应特征，本文采用弯曲-剪切耦合多自由度模型进行等效。剪力墙建筑的一个显著特点是在设计中主要考虑地震横波、强风等横向载荷的作用，通过合理布置的钢筋混凝土剪力墙构件，使得建筑整体上获得较高的抗弯刚度来抵抗上述载荷。因此已有研究中大多采用“糖葫芦串”的纯弯曲模型[15]，即将建筑视为纯单边固支Euler梁，剪切刚度设定为无限大，认为建筑结构在一般的横向载荷下只发生纯弯曲变形而没有剪切变形。这对于一般载荷是合理的，但对于强爆炸冲击波这一压力峰值较高的冲量型载荷，上述近似可能并不成立。特别是对于壁式框架等剪力墙建筑结构，容易产生明显的层间剪切应变，出现明显的剪切型变形，因此除弯曲外必须考虑其剪切特性。本文在简化时对剪力墙结构采用了Miranda等[16]和熊琛等[17]提出的弯曲-剪切耦合模型，如图1所示。

(a) Shear wall building

(b) Model

弯曲-剪切耦合模型在结构等效层面将一层建筑离散为一个集中质量自由度，单层采用一根非线性弯曲弹簧和一根非线性剪切弹簧来表征其力学特性，并采用一根刚性链杆进行连接，保持应变一致，通过这样一个单元来分别代表楼体受强爆炸作用后产生弯矩和剪力的反应。对双重受力体系的剪力墙结构，如框剪结构或框筒结构等，采用弯曲弹簧模拟剪力墙构件，剪切弹簧模拟框架构件，能更全面地展现其结构力学特性。与一般纯弯曲多自由度模型相比，该模型充分考虑了剪切变形的影响，认为结构存在较大但数值有限的剪切刚度，比纯弯曲模型更合理，能计算得到每一层处的剪切应变分布情况。

多自由度弯曲-剪切耦合模型控制方程可表示为

(1)

1.2 计算参数预估

求解上述控制方程首先需确定多自由度等效结构的E，G等参数。如何便捷且较为准确地获取相关参数，是开展快速计算的一个重要前提。上述参数同结构的一阶和二阶振动周期有密切联系，结构一阶和二阶周期的获取方法主要有：(1)高层结构在设计时通常进行了模态分析，可采用模态分析得到的平动一阶和二阶周期，相应的LS-DYNA也添加了振动分析模块；(2)某些重要高层建筑往往布置了结构监测设备，可根据监测结果计算得到结构的一阶和二阶周期；(3)对一般高层建筑，可采用经验的周期确定方法，如我国RC高层结构的一阶周期可根据建筑结构荷载规范(GB 50009-2012)[18]进行确定。一阶和二阶周期可表示为

(2)

T1′=(0.05～0.10)×n

(3)

T2=0.27T1

(4)

其中：T1为框剪结构的一阶周期；T1′为纯剪力墙结构的一阶周期；T2为结构的二阶周期；H为建筑总高度；B为建筑宽度；n为楼层数。式(4)为经验公式。

得到结构的一阶和二阶周期后，可推算结构的弯剪刚度比α0，表示为

(5)

(6)

其中，γj为第j阶结构振动相关的特征值参数，该值是结构弯剪刚度比α0的函数，α0定义为

(7)

圆频率ω1可表示为

(8)

确定了结构弯剪刚度比之后可根据一阶周期对应的圆频率ω1及式(8)确定结构的弯曲刚度E，再根据式(7)确定结构的剪切刚度G。一般根据其建筑面积S来估算结构的集中质量。经验上，剪力墙类建筑每平方米建筑面积需消耗0.47 m3钢筋混凝土，钢筋混凝土密度取2 600 kg·m-3，将估算质量均匀集中在每一层楼体处即可估计得到mi。

综上，通过建筑结构的高度、宽度、层数、结构类型及面积等结构属性参数可实现对多自由度模型的参数估计，从而满足动力学方程求解条件。MDOF方法以楼层为单位对整个建筑进行离散，自由度可控制在100左右，故在给定爆炸载荷的条件下，可实现建筑整体动响应的快速计算。

2 动力学响应计算与分析

2.1 多自由度程序计算

以某真实纯剪力墙住宅建筑为例，采用MDOF方法对给定爆炸载荷下的动响应进行计算验证。计算相关具体参数如表1所列。

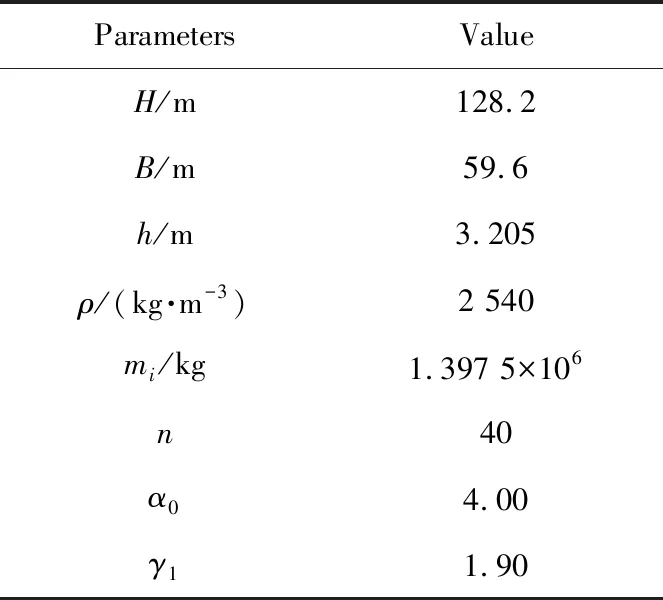
表1 目标剪力墙建筑模型相关参数Tab.1 Model parameters of target shear wall building

定义强爆炸载荷在空间上以平面波形式加载至建筑表面，考虑到Kingery-Bulmash(K-B)爆炸模型的合理性和应用的广泛性，压力-时间曲线采用K-B爆炸模型。K-B爆炸模型分布如图2所示。由图2可见，K-B爆炸模型近似为三角波形分布，压力峰值为53.69 KPa，三角波形压力持续时间约为2.4 s。

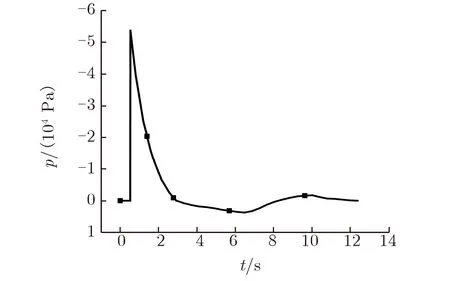
图2 K-B爆炸模型波形分布Fig.2 Waveform of K-B blast model

首先，对建筑物信息进行结构弹性参数估计，由式(2)-式(4)估计得到结构的一阶和二阶周期分别为T1=3.87 s，T2=1.044 9 s。得到结构一阶和二阶周期，即可计算出结构的弯曲刚度E=2.554 7×1010N·m2及剪切刚度G=2.487 0×107Pa·m-1，进而可得到结构的动力学响应。通过多自由度计算给出剪力墙建筑最顶层的挠度X随时间的变化关系，如图3所示。由图3可见，挠度最大为3 601 mm。

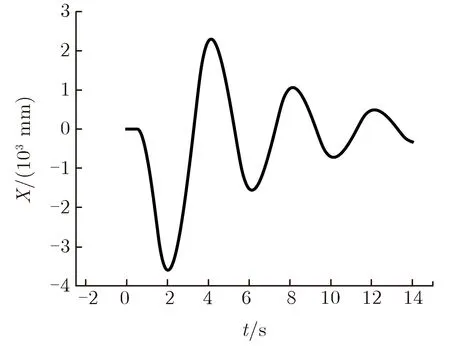
图3 剪力墙建筑最顶层的挠度随时间的变化关系Fig.3 The top floor deflection of shear wall buildings vs. time

面对强爆炸载荷这一冲量类短时程载荷，其高阶变形与高阶响应可能对最终的挠度变形具有较大贡献。因此,对动力控制方程式(1)，本文采用模态分解的方式开展计算。结构的模态分析和振动模式主要与结构的参数和边界条件密切相关，可认为建筑与地面刚性强连接，得到非归一化的振动模态，如图4所示。

图4 剪力墙建筑等效后的非归一化振动模态Fig.4 Nonnormalized vibration modes of shear wall buildings

由图4可见：一阶模式为纯弯曲变形，整体无反弯点，即对应建筑结构的纯弯曲变形；二阶以上为高阶变形，曲线较为复杂，结构出现反弯点。高阶振动模态能体现出剪力墙建筑可能发生的剪切型变形特征。

通过计算爆炸载荷在不同模态下所产生的挠度，采用ABS方法进行组合，可得到整体结构响应及一阶和二阶模态的贡献值，如图5所示。

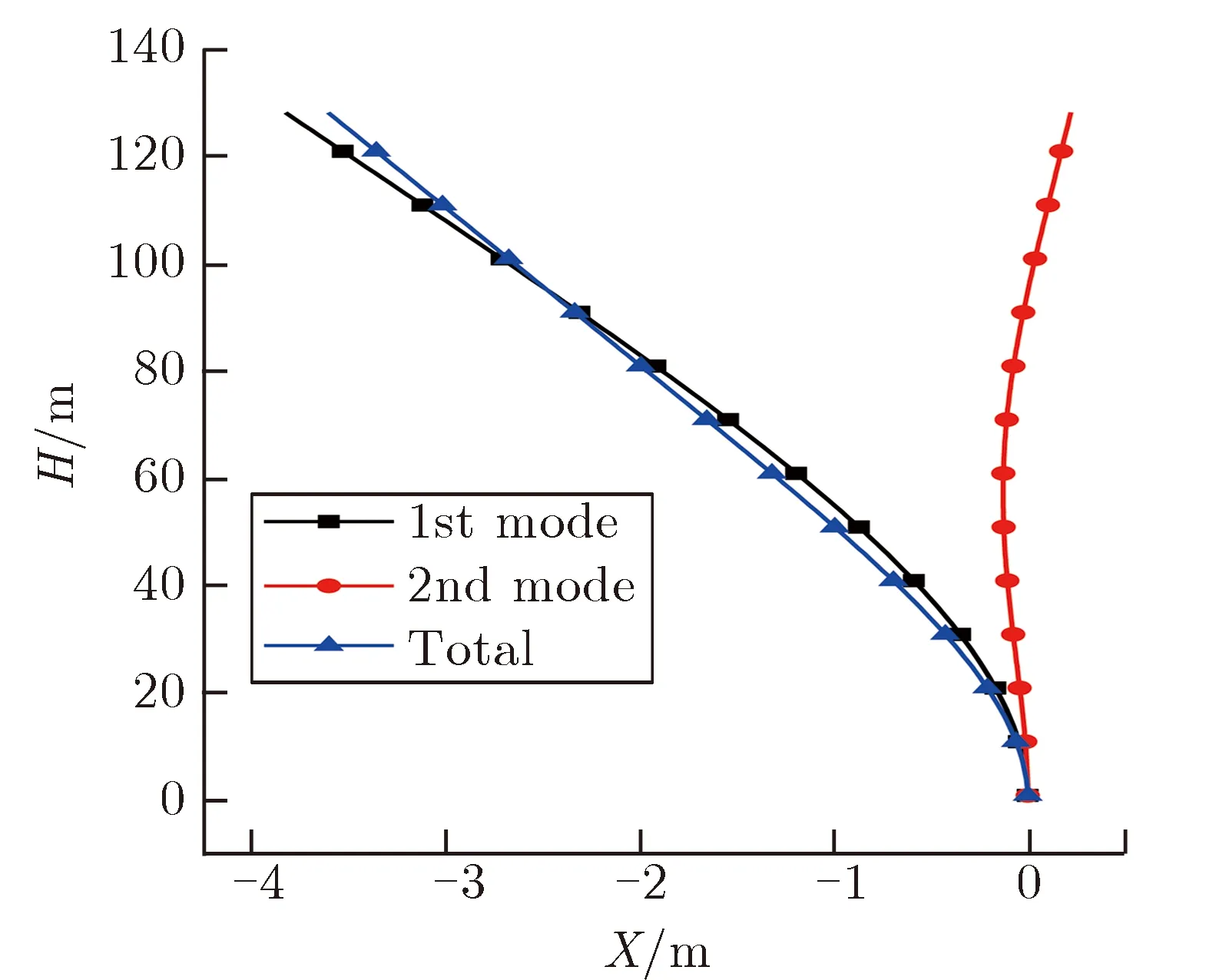
图5 整体结构响应及一阶和二阶模态的贡献值Fig.5 Overall structure response and the contribution of 1st and 2nd modes

由图5可见，三阶以上的模态可忽略不计，但二阶模态提供了无法忽略的挠度贡献值，整个结构的变形形状出现了一定的剪切变形特征。图6为一阶和二阶模态所提供的贡献随结构高度的变化关系。

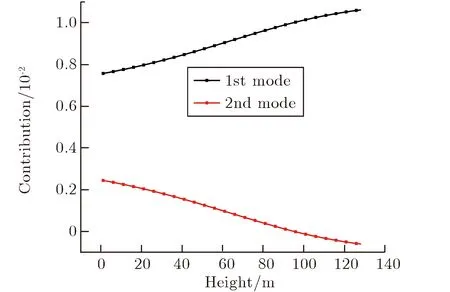
图6 一阶和二阶模态所提供的贡献随结构高度的变化关系Fig.6 The contribution of 1st and 2nd modes vs. height

由图6可见，在载荷冲击方向的总挠度中，二者贡献值并非常数。随着建筑高度的增加，一阶模态的贡献单调增加，二阶模态的贡献单调递减，二阶模态贡献的峰值在建筑基底部分达到24.2%，在建筑接近顶端处取负值。因此就本工况而言，二阶模态响应对于建筑的动响应行为有较大的影响。这也说明，对建筑而言，直接采用单自由度方法进行分析，并假设其为一阶纯弯曲变形可能存在不足，需采用多自由度方法进行描述。

针对建筑的破坏毁伤问题，特别是强爆炸载荷条件下建筑物的毁伤，目前尚未有较统一的定量划分标准，一般的参考指标为层间转角θ。通过层间转角对每一层可能发生的破坏进行度量。图7为本文算例沿高度方向各层间转角的分布。由图7可见，层数由高到低，层间转角逐渐增大，且最大层间转角出现在建筑物底层。

图7 沿高度方向各层间转角的分布Fig.7 Distribution of interstory drift angle

本文算例的最大层间转角为-9.900 899×10-4，略小于国标中RC抗震墙核心筒结构最大转角为1×10-3的要求，且小于RC框架中剪力墙最大转角为1.25×10-3的要求，因此，可认为该建筑结构在上述强爆炸载荷作用下是安全的。但本文所给定的工况条件下，已非常接近于非弹性响应的极限情况。同时，若将建筑视为一个整体，假设破坏发生在建筑基底附近，可采用支撑转角，即最大层间转角θm，进行判定，而这也是SDOF方法所采用的判定准则。支撑转角可表示为

(9)

其中，Xm为建筑顶点处最大水平挠度。通过计算θm为3.22°，而GB50779-2012[18]中对剪力墙建筑顶端的抗爆要求安全极限阈值为4°，因此，可认为建筑是安全的。

2.2 LS-DYNA数值模拟

FEM虽不满足耗时要求，但其相对准确的计算精度及丰富的计算结果可作为重要的参考依据，能验证多自由度弯曲-剪切耦合模型计算结果的准确性和合理性。针对上述计算工况，利用LS-DYNA商业有限元计算软件，与多自由度方法的计算结果进行比较。单元建模上剪力墙墙体与楼板采用shell单元，梁结构采用beam单元。对RC材料，基于连续均匀性假设，不考虑具体的钢筋配置与混凝土分布，采用*MAT_PLASTIC_KINEMATIC模型进行均匀化处理，虽在局部难以观察到超筋和少筋等具有脆性特征的破坏模式，但对百米量级建筑整体的动力学响应模拟计算，单元特征尺寸为几十厘米，这种材料建模处理方法是合理的。爆炸载荷同为K-B爆炸模型，爆炸载荷施加在均匀墙体一侧，所有节点均匀加载。结构边界约束为地面固定连接，其余节点均为自由节点。整体结构划分后楼板与墙体shell单元数为185 888。柱体级梁beam单元数为20 928。图8为剪力墙建筑多自由度弯曲-剪切耦合模型。

(a) Explosive load application boundary

(b) Boundary fixed connection图8 剪力墙建筑多自由度弯曲-剪切耦合模型Fig.8 Flexure-shear bonding multi degree of freedom model of shear wall building

整个结构发生横向水平位移的最大位置为结构顶点处。提取该点的挠度随时间的变化关系，如图9所示。

图9 建筑结构顶点的挠度随时间的变化关系Fig.9 Deflection of building structure vertex vs. time

由图9可见，在爆炸冲量载荷结束后，建筑结构的自振周期约为3.55 s，这与多自由度方法的估算结果及LS-DYNA中自带的模态分解模块的计算结果均较接近。强爆炸载荷存在明显压强的持续时间约为2.4 s，在该时刻结构顶点挠度达到了最大值4.32 m，对应的转角为0.03，该时刻的结构整体变形情况及等效应力分布如图10所示。

(a) 3-D view

(b) x-z view

由图10可见，建筑物顶部产生最大水平挠度时，整个建筑呈现出典型的弯曲型变形，建筑结构横向位移随着高度增加而增加，没有出现明显的剪切错位情况，证明剪力墙结构发挥了较好的抗横向抵抗作用。Mises等效应力分布集中在建筑底部且靠近冲击载荷的一侧，从整体上看建筑基底处同地面的固连产生了有效的弯矩来抵抗横向冲击载荷。在结构失效破坏问题上，建筑目标并没有出现整体性的垮塌或是破坏，载荷结束后也没有发生连续倒塌现象，基本保证了外观无损。但统计计算结果发现，shell单元失效数为1 506，beam单元失效数为382。失效单元在整体结构中的分布如图11所示。

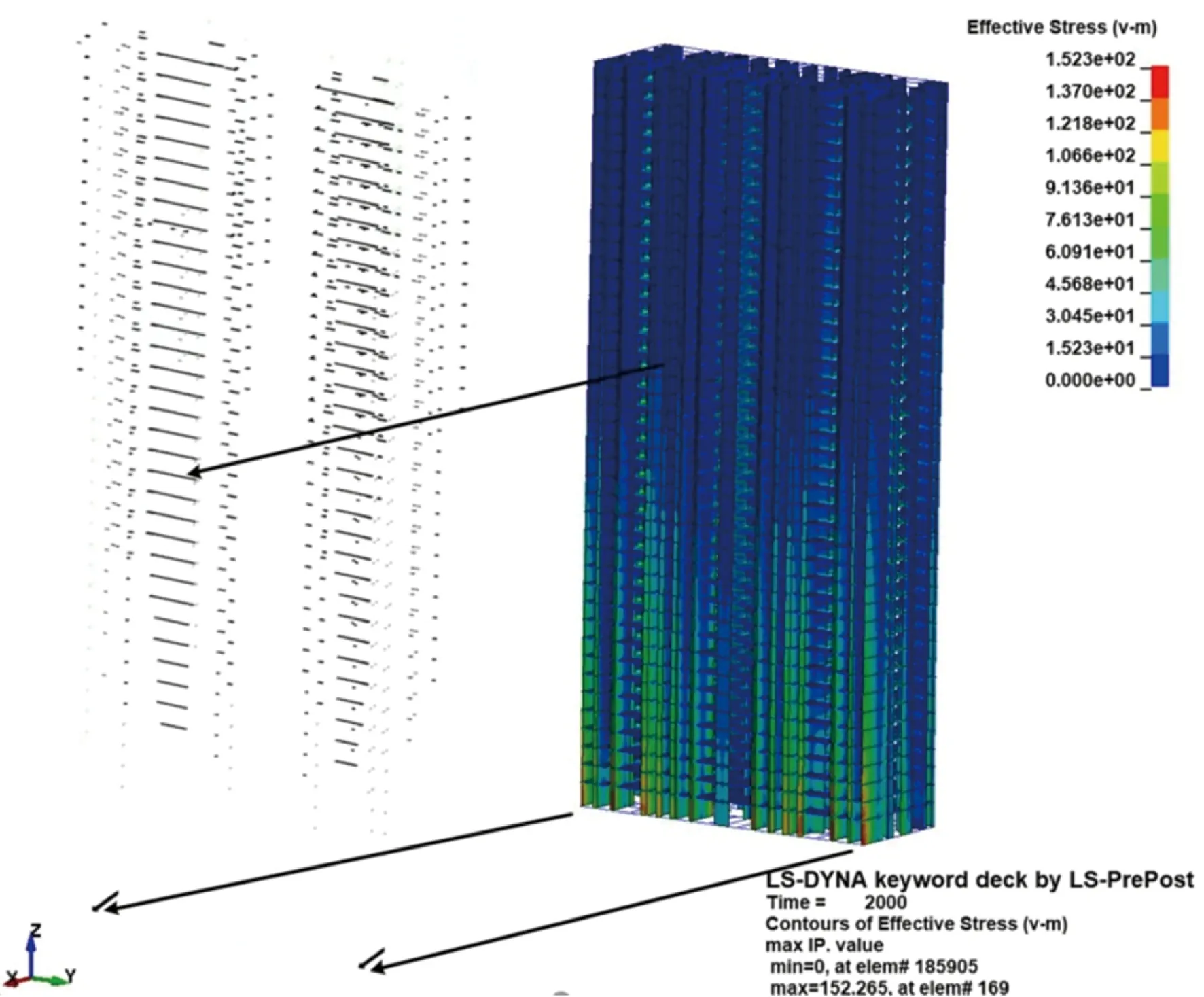
图11 失效单元分布Fig.11 The distribution of failure elements

由图11可见，在失效分布上，shell单元的失效主要为楼板结构而非受冲击的墙面结构，且分布密度由底到高逐渐增加。因此可认为单个楼层区域的横向楼板失效作为一种局部破坏对建筑整体的影响有限。更值得注意的是，在建筑基底处，虽然横向挠度最小，但在该处与地基固连的部分出现了集中连续的结构破坏，这一破坏现象与图10中出现的应力集中现象相符，而建筑基底处的连续性破坏会对建筑结构整体的安全造成重要影响。

沿建筑高度方向每8层取一个监测点，提取该处的横向挠度-时间数据，不同高度处结构的横向位移，即挠度随时间的变化关系如图12所示。由图12可见，各个区域处保持变形方向的同步性，即从振动的角度看，结构主要发生一阶弯曲模式的振动。将一阶纯弯曲的计算结果在建筑顶点处同FEM计算结果设定为相同，并进行归一化操作，将FEM计算结果同纯弯曲变形的对比，得到t=2 s时，相对高度随扰度的变化关系，如图13所示。

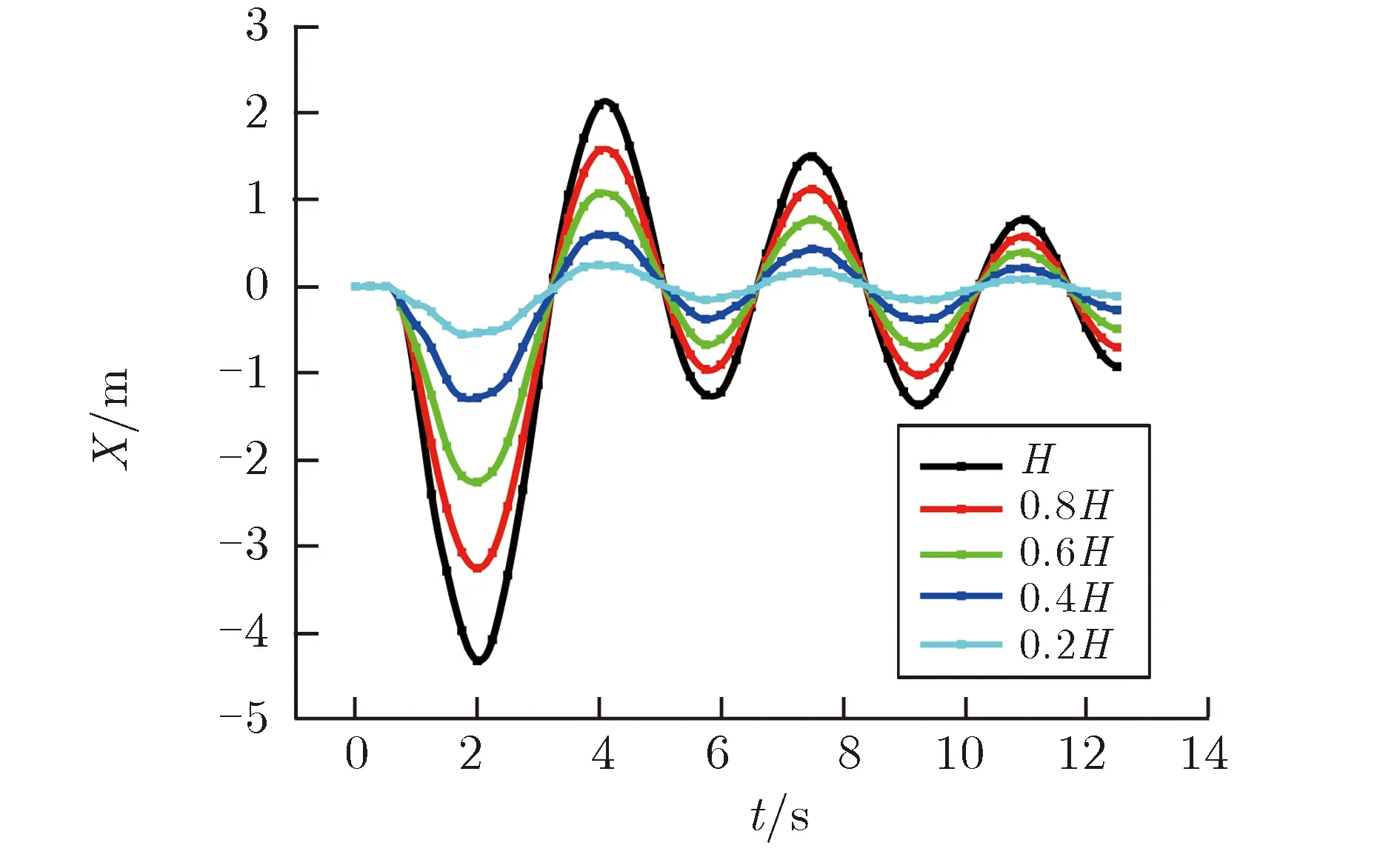
图12 建筑结构不同高度特征点分布情况Fig.12 Distribution of characteristic points of different height of building structure

图13 t=2 s时，相对高度随扰度的变化关系Fig.13 Relative height vs. deflection at t=2 s

由图13可见，不同高度处结构的扰度计算结果与理论纯弯曲计算结果很接近，但在低层处的相对偏差更明显，这说明建筑的变形模式上需考虑MDOF方法所得到的二阶以上模态的贡献。另一方面也证明了剪力墙类结构在上述爆炸载荷加载作用下，墙体结构发挥了很好的抗弯性能，使整个建筑结构在性能上保持了很好的整体性，变形类似于悬臂梁结构。而失效模式上，在建筑整体特别是纵向墙体上，并没有明显的失效破坏情况，与MDOF方法的计算结果一致，但在内部楼板处却出现了较多的壳体单元局部失效，这一局部失效现象是MDOF方法计算无法体现的，但并未对建筑整体的破坏出现重大影响。

与多自由度计算结果相比，LS-DYNA计算给出的建筑物顶端最大扰度为4.311 m，而多自由度程序计算结果为3.601 m，与LS-DYNA 的计算结果相对偏差为 16.2%。考虑到MDOF方法的近似程度及二者的计算时间(相同PC机条件下，LS-DYNA计算约需4 h，多自由度计算时间为秒量级，可忽略不计)，该计算结果可接受。在损伤判定问题上，LS-DYNA能展现结构破坏细节，整体建筑保持稳定，但各个楼层处的横梁及楼板结构发生破坏。多自由度方法无法得到细节情况，但整体结构判定上二者都没有发现建筑的明显破坏情况。