CT辐射系统模型在蒙特卡洛模拟中的构建方法研究进展*
2022-02-03刘颖孟婷路鹤晴章浩伟
刘颖,孟婷,路鹤晴,章浩伟△
(1.上海理工大学 健康科学与工程学院, 上海 200093;2. 同济大学附属第一妇婴保健院 设备科,上海 200092)
引言
医学辐射是电离辐射的主要来源之一[1]。目前,X射线被用于医疗照射所产生的辐射剂量在人体的整体剂量中占比最大[2],其中,CT检查是辐射剂量的主要来源[3]。国际放射防护委员会ICRP102号报告指出,在过去20年内,CT检查的使用频率在世界范围内增加了逾8倍[4]。“十一五”期间,关于上海市医学辐射水平的调研表明,2009年比1996年的X-CT检查,大幅度净增3.17倍[5]。因此,如何准确计算CT受检者所受的辐射剂量显得尤为重要。
在各类辐射剂量估算方法中,蒙特卡洛方法是一类以概率论为中心思想、具备随机性和不确定性的统计方法[6],被广泛应用于生物医学、粒子输运计算、核工程等领域。常见的蒙特卡洛程序包括MCNP (Monte Carlo Neutron and Photo Transport Code)程序、ESG (Electron-Gamma Shower)程序、FLUKA (FLUktuierende KAskade) 程序等。利用蒙特卡洛程序准确计算人体在CT检查时所受的辐射剂量,需要建立准确的CT辐射系统模型,简称CT模型。CT模型的具体构建顺序为获取X射线能谱、设计蝶形过滤器形状、构建准直器模型和模拟球管的旋转运动。随着CT技术的不断提升,国内外有许多研究者提出了CT辐射系统模型在MCNP模拟中的构建方法,并且建立了不同类型的CT模型。本文按照CT辐射系统的建模顺序分别对这些方法进行综述,为相关领域的研究者以及后续的研究方向提供参考。
1 国内外研究者构建的CT模型
首个完整的CT辐射系统模型由澳大利亚的Caon等[7]于1999年建立,他们利用EGS程序建立了一台GE Hi-Speed Advantage CT模型,并对MIRD (Medical Internal Radiation Dose)人体模型进行了剂量估算。随后,英国的Khursheed等[8]利用MCNP分别建立了西门子DRH、GE 9800和飞利浦LX模型,并对从新生儿到成年人的各阶段人群进行了剂量估算与对比。2003年,美国的Jarry等[9]提出了单排螺旋CT的建模方法,并利用MCNP构建了GE HiSpeed CT/i CT模型,且对MIRD 体模进行了剂量验证。在此基础上,同研究团队的DeMarco等[10]于2005年首次构建了一台GE LightSpeed 16排CT模型,并对标准体模进行了剂量验证。同年,希腊的Tzedakis等[11]利用MCNP建立了西门子 Sensation多排螺旋CT的辐射系统模型,并根据实际扫描条件计算了体模所受的剂量。西班牙的Salvado[12]利用EGS建立了GE HiSpeed LX/i CT模型,并对仿真体模和人体体素模型的辐射剂量进行估算。2009年,美国的Gu等[13]首次详细描述了GE LightSpeed 16排CT的建模技术路线,代表着完整CT建模体系的形成。随后的研究都是在此基础上进行建模方法的改进。2011-2013年间,美国的Lee及其团队[14-15]不断提出了CT模型的改进方法,并增强了西门子Sensation 16排CT的准确度。直到2014年,清华大学的潘羽晞等[16]在Gu等[13]的技术路线基础上,利用MCNP建立了GE LightSpeed 16排CT模型,并首次估算了一个符合中国人体征的儿童模型所受的辐射剂量。2014年至今,研究者们致力于研究CT建模的每个环节,分别从精准的测量仪器、物理测量方法和理论算法角度提升模型的准确度。
2 获取X射线能谱
X射线谱包含轫致辐射和特征辐射。当入射高速电子与原子核碰撞,其部分或全部动能变为产生的光子的能量,由此产生的X射线称为轫致辐射。X射线管的管电压超过某一临界电压时,在某些特定能量值处会出现强度很高、非常狭窄的谱线,它们叠加在连续谱上,即为特征辐射[17]。在蒙特卡洛模拟中,为简化放射源模型,通常将初始X射线穿过固有滤过后的能谱视作放射源能谱,用以描述光子能量的抽样分布。获取X射线能谱的方法主要分为以下两种:
(1)由厂家提供球管几何参数,输入并由软件生成X射线能谱。
从上个世纪80年代以来,陆续有研究者开发了X射线能谱软件(见表1)。这些软件的理论原理分别来自半经验模型、蒙特卡洛模拟和两种方法的结合。可通过在软件中输入厂家提供的阳极靶角、固有滤过厚度等几何参数来获得X射线能谱。Caon等[7]利用Tucker等[18]提出的半经验模型来获得能谱。Khursheed等[8]、Salvado等[12]和Lee等[14-15]利用IPEM78[19]和厂家提供的数据生成CT模型的X射线能谱。Tzedakis等[11]利用TASMIP[20]来生成X射线能谱;Gu等[13]和潘羽晞等[16]利用了XCOMP5R[21]生成X射线能谱。
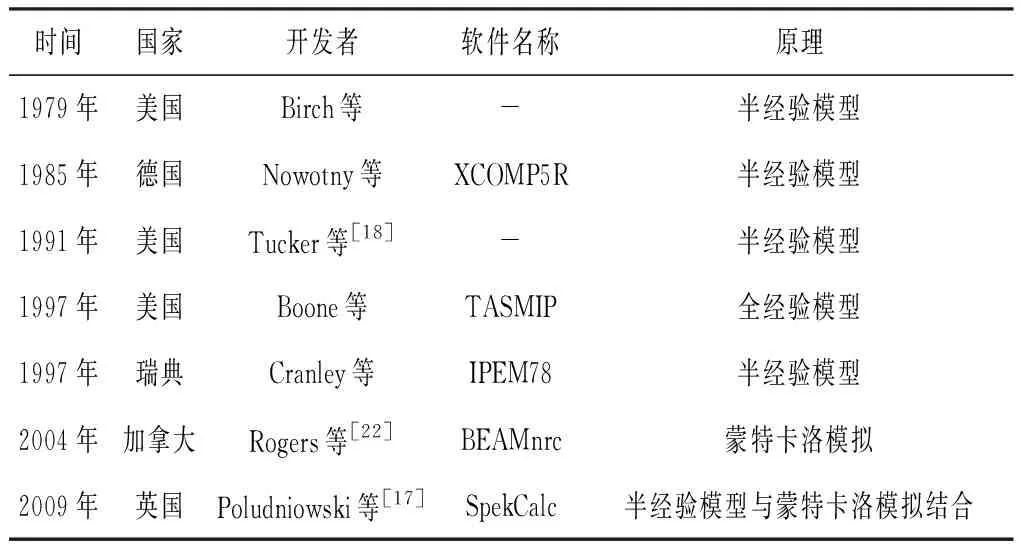
表1 现有的X射线能谱软件及其原理
Rogers等[22]通过对比实验值和蒙特卡洛模拟值,验证了由蒙特卡洛模拟生成的能谱精度要高于半经验模型生成的能谱。Poludniowski等[17]通过在不同能谱软件中输入相同的球管参数,发现基于蒙特卡洛模拟的能谱软件之间的输出结果最大差异小于3%,而基于半经验模型的能谱软件的最大差异为6%。由此可知,在模拟X射线源时,采用半经验模型生成的能谱会给结果带来较大误差。
(2)测量X射线球管在一定管电压下的半值层,在能谱软件中匹配测量的半值层来获得X射线等效能谱。
半值层(half-value layer,HVL)为使辐射束的空气比释动能减少到其初始值一半时,指定材料的厚度,通常用mmAL表示[23]。半值层是X射线能量表达的重要参数,因此可以通过匹配实验室测量与软件输出的半值层来获得X射线等效能谱。等效能谱的概念由Turner等[24]于2009年提出。他们对比了基于厂家给出的数据所构建出来的源模型和基于半值层获得的源模型,发现前者与实际测量所得的CT剂量指数(CTDI)的均方根误差最高可达20%,而后者最高仅为7%,这代表等效能谱可在很大程度上提升模型的准确性,而仅靠厂家提供的数据会给模型带来较大误差。
3 设计蝶形过滤器形状
人体的横截面类似于一个椭圆,当X射线穿过人体时,中心处吸收的能量要高于边缘处,这导致边缘皮肤剂量增大,因此,需把过滤器设计成蝶形,才能使能量分布均匀。由于蝶形过滤器的形状复杂,且不同CT之间差异巨大,因此该结构为CT建模中最难的部分。为了在蒙特卡洛模拟中设计出蝶形过滤器的具体形状,需要获得其厚度角分布,即过滤器厚度关于X射线角度的函数。获得蝶形过滤器厚度角分布依赖于实验室测量,方法大致有3种:
(1)测量标准体模中心与边缘的CTDI比值,简化蝶形滤波器模型,再通过调整简化模型来使模拟值贴近测量值。
Gu等[13]和潘羽晞等[16]在构建GE LightSpeed 16排CT模型时,利用长方体减去一个椭圆柱的方式来构建蝶形过滤器的简化模型,见图1。通过不断调整椭圆的长短轴来使模拟与测量的标准体模中心与边缘的CTDI比值偏差小于5%,这时认为该简化模型可代替蝶形过滤器模型。
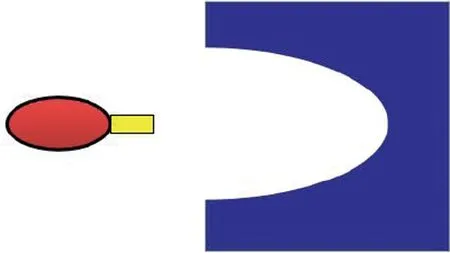
图1 蝶形过滤器简化模型(蓝色部分)
(2)测量静态剂量曲线,计算获得蝶形滤波器的厚度角分布。
Turner等[24]将X射线球管固定在90°的位置来测量多个偏离等中心点处的空气比释动能。各个测量点的间距为5~10 mm,见图2。根据测量的结果可以得到横坐标为X射线角,纵坐标为空气比释动能的静态剂量曲线。根据曲线可以得到每个测量点与等中心点的空气比释动能比值。该蝶形过滤器的材料为铝,可以通过查询NIST报告来获得铝对于不同能量光子的衰减系数,再根据上一步所获得的等效能谱,利用能量衰减公式来获得蝶形过滤器厚度角分布。通过模拟实验测量发现,实验值与模拟值的均方根误差小于5%。基于上述理论,Lee等[14-15]获得了西门子Sensation 16排螺旋CT的蝶形滤波器模型,发现实验值与模拟值的均方根误差小于3%;Hassan等[25]也利用了该方法构建了西门子Definition 64排CT的蝶形过滤器模型,且由于剂量计的精度增高,实验值与模拟值的均方根误差仅小于1.16%。该CT模型具有两种不同形状的蝶形过滤器,通过计算发现,这两种过滤器的形状都与椭圆相差甚远。由此可知,Gu等[13]提出的模型简化法并不适用于所有CT的蝶形过滤器模型,反而会给模型带来较大误差,而通过静态剂量曲线的方式来获得的模型会更加精确。
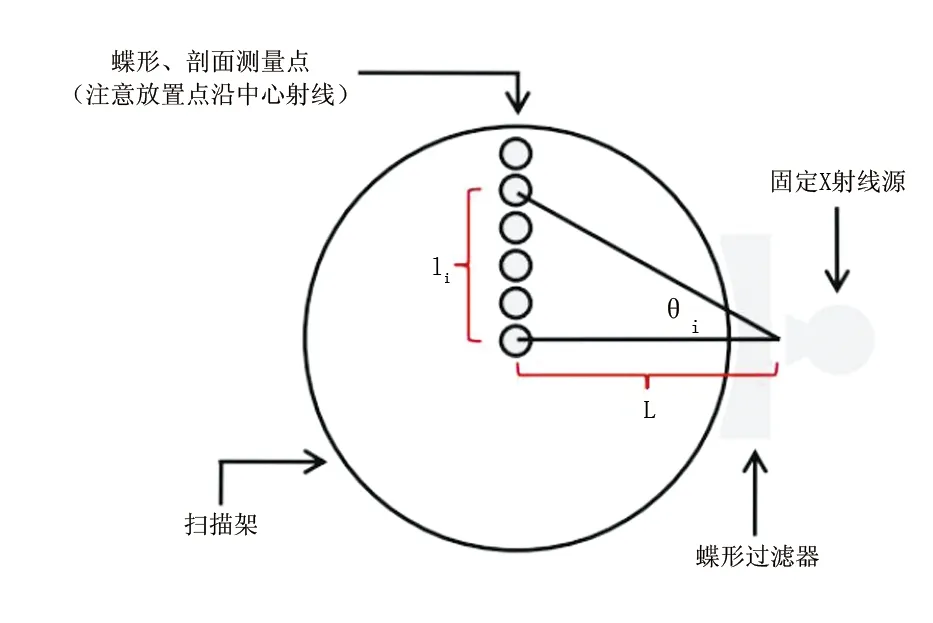
图2 静态剂量曲线的测量示意图
(3)测量旋转剂量积分曲线,计算获得蝶形滤波器的厚度角分布。
有别于静态剂量曲线,旋转积分剂量曲线是不固定球管的位置,并利用探测器测量球管旋转过程中的剂量变化,获得蝶形过滤器的厚度角分布。该测量方法由Boone提出,命名为COBRA(characterization of bowtie relative attenuation,COBRA)法[26]。测量方式见图3,剂量计位于视野的边缘,通过X射线的平方反比定律可以获得测量点与等中心点的空气比释动能关系,见式(1)。
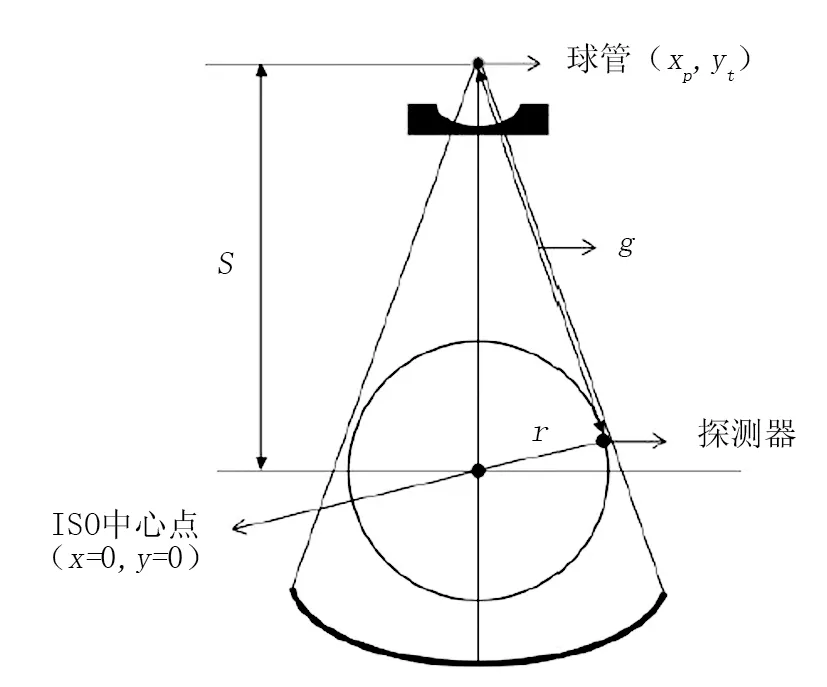
图3 旋转积分剂量测量图Fig.3 Schematic diagram of rotating integral dose measurement
(1)
其中,M(α)为测量点的空气比释动能,F(θ)为蝶形过滤器导致X射线在θ角的衰减系数,s为X射线源点到等中心点的距离,g为X射线源点到测量点的距离,I0为等中心点的空气比释动能。
随着球管旋转一圈,对式(1)两边求取角度为0到+2π的积分,根据剂量计的测量值,可以得到F(θ)的函数关系式,从而获得蝶形过滤器的厚度角分布。
在Boone的基础上, McKenney等[27]将该方法应用在一台西门子乳腺CT的模型构建中,将构建的蝶形过滤器与厂家提供的模型进行对比,发现二者的厚度角分布差异均小于2%,该建模方法的优越性在于可以分析计算出多种材料组成的蝶形过滤器,并且可以达到较好的准确度;而不足在于对剂量计的时间灵敏度要求很高,无法大范围应用于其他的研究工作,且无法在球管旋转的情况下获得半值层。
随后,Whiting等[28]、Randazzo等[29]和 Hassan等[25]分别从剂量计、测量方式和理论算法来弥补COBRA法的不足,其模拟值和实际测量值均有高度一致性。
4 构建准直器模型
在蒙特卡洛模拟中主要是针对前准直器进行建模,CT的前准直器能够减少受检者的辐射剂量,并能限定X射线的扫描范围。可以通过以下方式来建模:
(1)利用蒙特卡洛程序内的功能函数,直接实现粒子截断。
MCNP程序中内置有cookie-cutter函数,可以记录一定范围内的粒子,舍弃超出范围内的粒子。利用这一点,Gu等[13]和潘羽晞等[16]在放射源附近建立了一个立方体来限定X射线的照射范围,即图1中的黄色部分。根据源到长方体右侧底面和到等中心点的距离之比可以调整前准直器宽度,因此该方法比较便利。
(2)建立实际的几何体来限定光子飞行的范围。
Lee等[14-15]对此准直器的建模方法进行了详细阐述,并提供了模型示意图。首先建立几个圆柱并进行布尔运算,其次在放射源附近形成仅容一定光子通过的缝隙,且不允许光子穿过缝隙外的空间,最后形成准直器模型,该方法的原理与第一种方法相似。
5 模拟球管的旋转运动
为了生成CT图像,球管需要通过旋转采集各角度的信号。现有的蒙特卡洛程序无法描述一个不断运动着的放射源,因此,研究者们通过对不同位置源进行抽样来模拟球管旋转一周的情况。
Khursheed等[8]分别对比了一周布置18和72个抽样点的CTDI模拟结果,发现二者差异较小,认为18个角度抽样点足以等效模拟球管旋转一圈的情况。Gu等[13]同样对比了24和32个抽样点的CTDI模拟结果,发现二者差异小于5%,综合考虑下,他们采用了16个角度抽样点来模拟球管旋转一圈的情况,最后获得了与实验值相差较小的剂量模拟结果。
6 讨论和总结
本文针对CT辐射系统模型在蒙特卡洛模拟中的构建方法展开了综述。按照CT建模顺序,即获取X射线能谱、设计蝶形过滤器形状、构建准直器模型和模拟球管的旋转运动,分别对国内外研究者构建的CT模型进行了讨论和对比。为了获得准确的CT模型,对于X射线能谱,研究者应尽量使用基于蒙特卡洛模拟建立的能谱软件,并通过匹配实测半值层的方式来获得X射线等效能谱;对于蝶形过滤器,研究者应结合自身实验条件,选择静态剂量法或旋转积分剂量法来获得厚度角分布;对于准直器模型和球管的扫描运动,目前的模拟方法比较统一,因此研究者可自行选择。
另外,通过分析发现,目前研究的CT大多数来自于GE和西门子,不同CT种类内部的结构,尤其是蝶形过滤器差异较大,急需提出一种通用的、准确的模型构建方法,应用于各类CT中。该建模方法应融合并改进国内外研究者提出的方法,形成一套完整的CT建模系统。考虑到蒙特卡洛程序的输入文件结构复杂,且CT模型几何参数,尤其是蝶形过滤器几何参数的计算过程繁琐,因此,该建模系统不仅需要支持CT模型实时三维可视化,还需要根据输入的实测物理量来计算几何参数,自动生成蒙特卡洛程序的输入文件,降低CT建模工作难度。本文虽然对比讨论了目前CT建模较为准确的方法,但是随着剂量仪测量精度的不断提高以及CT扫描技术的不断发展,CT建模方法也应不断改进。
