河北黄骅港附近海域潮汐特性分析
2022-02-03邢硕,刘杰,熊伟
邢 硕,刘 杰,熊 伟
(天津水运工程勘察设计院有限公司,天津 300456)
地球上的海水,在月球和太阳的作用下产生的一种规律性的上升下降运动为潮汐,潮汐的主要成因是由于地球表面上各点离月球和太阳的相对位置不同,各点所受到的引潮力有所差异,从而导致海水的相对运动。海岸附近和河口区域,是人类进行生产活动十分频繁的地带,而在这个地带潮汐现象显著,它直接或间接地影响着人们的生产和生活。例如,沿海地区农田排灌、海滩围垦、水产的捕捞和养殖、航海、筑港,以至于利用潮能发电等,无不与潮汐涨落有着密切的关系。因此,潮汐在沿海农田水利、滩涂围垦、建港、航道整治、捕捞、养殖以及潮能利用和对许多地球物理现象的研究以及为国防服务等方面,其作用十分重要和广泛,是促使潮汐科学发展的基本动力[1]。
国内很多专家学者对潮汐分析及其应用做了大量研究,黄祖珂、徐汉兴等论述了调和分析的原理和方法[2-3];石景元、范东华、李振云、熊伟等基于不同海区的实测潮汐资料,进行相关海域的潮汐性质分析[4-7];李阳东等分别对位于近海、河口、内河感潮河段等3种区域的验潮站的预报结果与潮位数据进行对比分析[8];吴富梅等对大港验潮站处海洋潮汐以及国家高程基准面近60 a的变化进行了分析和研究[9];孙磊等研究利用潮汐性质相似性判断指标和基于余水位配置的潮汐推算方法恢复缺测数据的可行性,并分析了推算精度[10]。
本文研究区域为河北省黄骅港附近海域。黄骅港位于河北省和山东省交界处,海上距天津60 n mile,陆上112 km;东距龙口约149 n mile,陆上280 km;西距黄骅市45 km。现有各类生产性泊位40个(不含东渡旅游码头),其中万吨级以上泊位35个,最大泊位吨级为20万t,包括煤炭港区、综合港区、散货港区和河口港区[11]。
2020年—2021年,在河北黄骅港附近海域设置CW1、CW2、CW3共三个观测站(图1),按春夏秋冬四季开展潮位观测工作,每站每季观测一个月,观测基准采用1985国家高程基准[12]。本文基于这次的观测数据和这些研究成果,对黄骅港附近海域的潮汐性质、潮位特征值、理论最低潮面、平均海平面、余水位等进行分析计算。
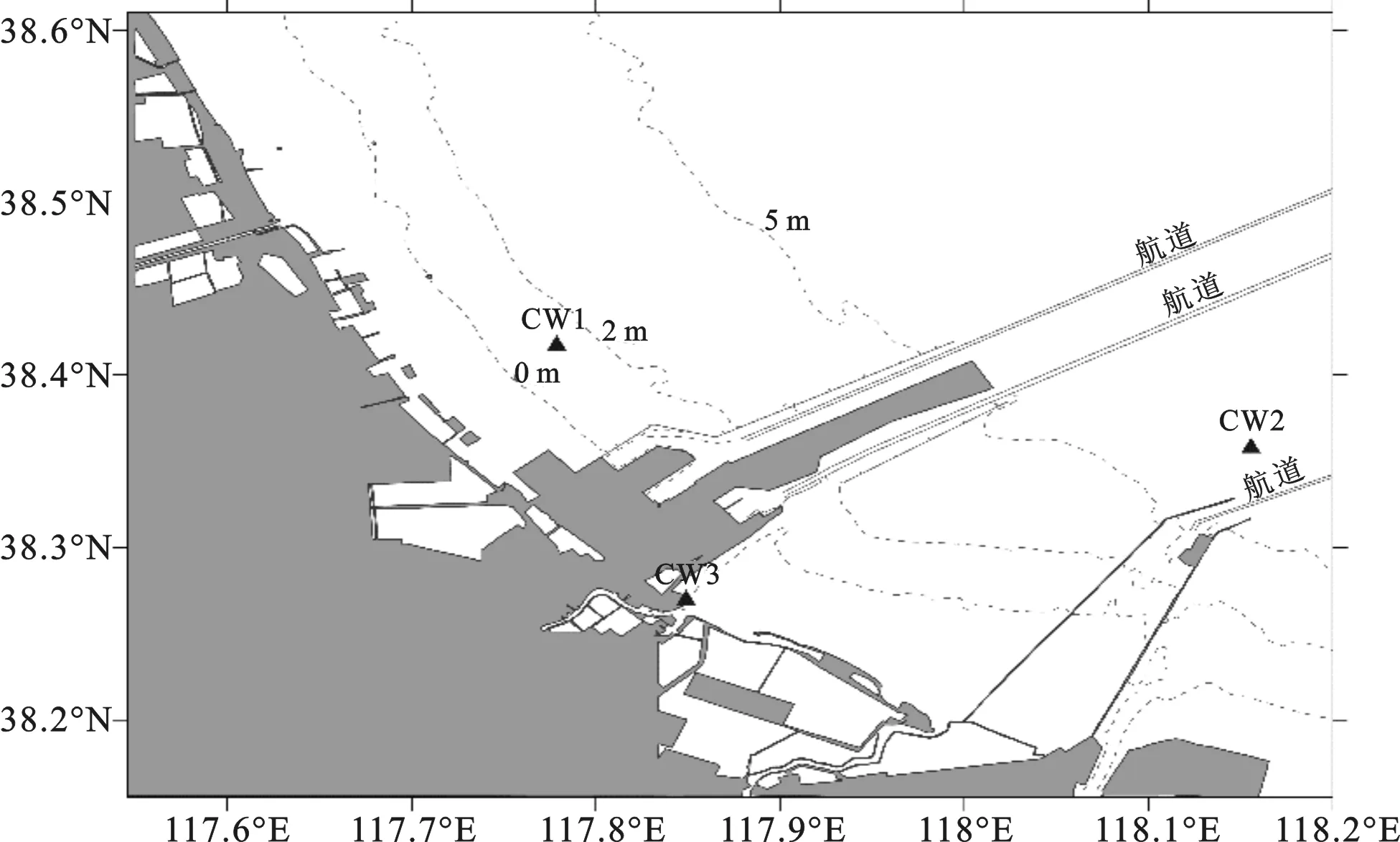
图1 潮位站布置示意图Fig.1 Schematic diagram of the layout of the tide stations
1 潮汐调和分析模型
在实际潮位中,由引潮力直接引起的潮位变化叫引力潮或天文潮,为水位变化的主要成分。除此之外,还存在着气象潮、天文-气象复合潮和浅水潮,与天文潮共同构成实际水位中的可预报成分。气象扰动引起的水位不规则变化是观测资料中的噪声,它是引起分析结果误差的主要来源。现有的分析方法很多,分析精度也相近,基于最小二乘法原理得出的调和分析方法简便实用,因此本文采用该方法进行调和分析。
海洋中的实际水位包含许多分潮振动,潮汐调和分析的目的,是依据实测水位资料获得该地各分潮的实际平均振幅以及各分潮的实际相角与平衡潮理论相角的差值(调和常数),从而掌握海区的潮汐特征。
则假设分潮个数为m,表达式为
(1)
式中:MSL为平均海平面高度;H为分潮的振幅;σ为分潮角速率;v为分潮的天文初相角;g为分潮的迟角。对于某一分潮,σ和v可以通过天体运动推算得到,H和g为分潮调和常数,是该分潮在某点振动变化的参数。式(1)是纯粹形式上的潮汐调和分析的潮高表达式。分潮的调和常数反映了实际海洋对这一频率天体引潮力的响应。这种响应决定于海洋本身的几何形状及其动力学性质,也决定了实际海洋中的分潮振幅与平衡潮引潮势展出的分潮系数不完全成比例。同时,由于海洋环境变化非常缓慢,就一般海区而言,调和常数具有极大的稳定性。
根据2020年06月15日~2020年07月16日(夏季)、2020年08月25日~2020年09月25日(秋季)、2020年11月28日~2020年12月29日(冬季)、2021年04月04日~2021年05月05日(春季)期间的潮位观测数据(1985国家高程基准),采用最小二乘法进行潮汐调和分析[13],得出11个主要分潮的调和常数。
2 潮汐性质
潮汐性质可分为正规半日潮、不正规半日潮、正规全日潮和不正规全日潮,潮汐性质以主要全日分潮与主要半日分潮的平均振幅比值F(示性系数)来判别
潮汐示性系数按下式计算
(2)

表1 各潮位站每季度潮汐示性系数Tab.1 The ratio of (K1+O1) to M2 of the stations for each quarter
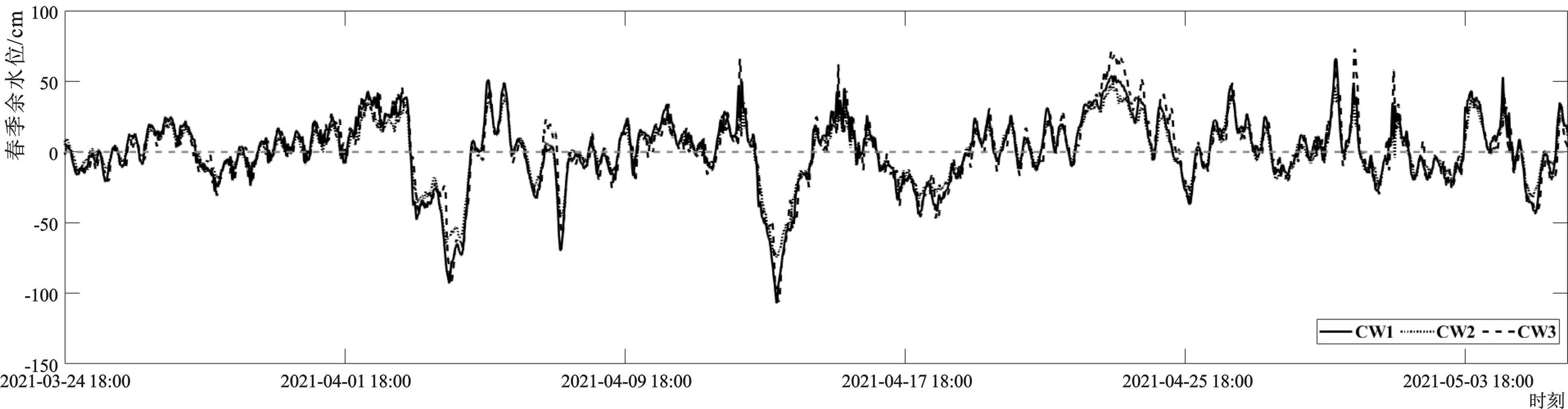
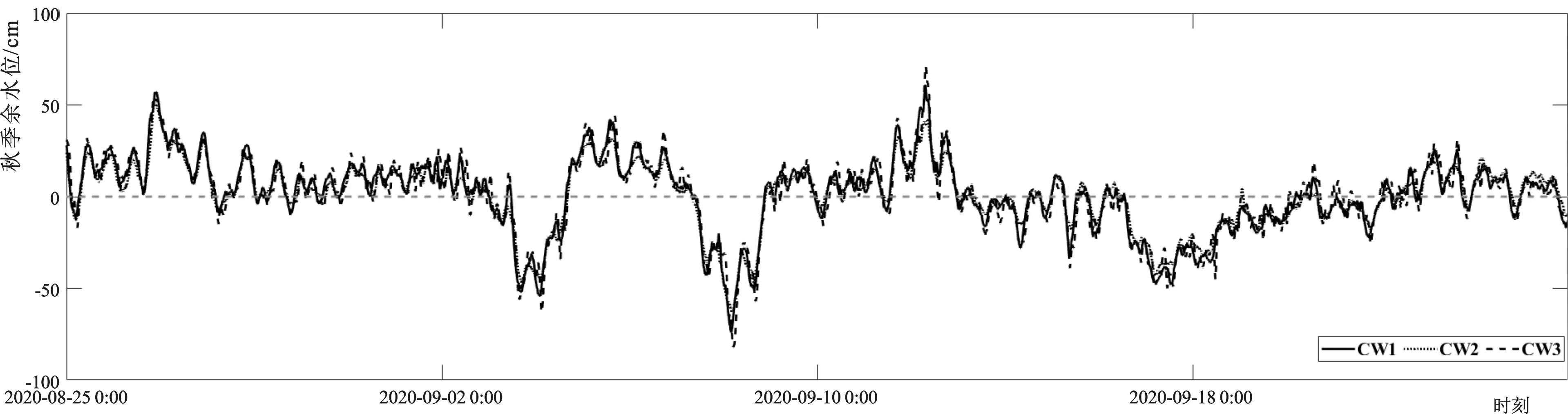
当F≤0.5时,为正规半日潮;当0.5 通过(2)计算每个季节各个站潮汐示性系数,结果如表1所示。CW1~CW3站计算结果均表明:该海域的潮汐属于不正规半日潮性质,各测站存在日潮不等现象,即相邻高潮或低潮的潮位不等、涨潮历时与落潮历时不相等。该结果与2014年—2015年对黄骅港的分析一致[14],符合黄骅港海域的潮汐性质特征。 通过对三个潮位站的四季潮位数据进行统计,得到各站每季度的潮位特征值如表2所示。观测期间,各测站实测最高潮位夏季最高、冬季最低,实测最大潮差春、夏季大于秋、冬季,平均潮差秋季最大、冬季最小。CW1和CW3平均涨潮历时皆小于落潮历时,CW1站平均涨落潮历时差为1 h 7 min,CW3站平均涨落潮历时差为1 h 20 min。CW2站涨落潮历时差距不大,春、夏、秋季皆为涨潮历时略大于落潮历时,冬季为落潮历时略大于涨潮历时,与调和分析的结果一致。平均涨、落潮历时差CW3站最大,四季间略有差异,表现为秋冬季略大于春夏季。 表2 每季度各潮位站特征值Tab.2 Tide level characteristics of each station for each quarter 图2 潮位站每季度月平均海平面Fig.2 Monthly MSL of the stations for each quarter 根据潮位站四季观测数据,计算每季的月平均海平面,结果如图2所示。平均海平面的变化,主要受天文、气象等因素的影响。可知,各站月平均海平面基本一致,秋季平均海平面为四季最高,其次为夏季和春季,冬季最低。四季月平均海平面变化趋势与自然资源部海洋预警监测司发布的2020年—2021年中国海平面公报中的河北月平均海平面变化规律基本一致。 表3 各站理论最低潮面值Tab.3 LAT of each station cm 采用潮汐调和分析得到的主要分潮调和常数,根据《水运工程测量规范》(JTS131-2012)[15]附录F进行理论最低潮面的计算,按四季分别计算CW1~CW3站的理论最低潮位,得到各站理论最低潮面如表3所示。表3数据表明:该海域理论最低潮面呈现CW2-CW3-CW1逐渐变大的特性,这与各站平均潮差变化规律一致,其中CW1站最大,CW2站最小,两站每季计算结果平均差约为46 cm。理论最低潮面的季节变化为从冬季到秋季逐渐增高,秋季为四季最高,冬季最低。 余水位是实测潮位与预报潮位差异的综合体现,其大小反映实测潮位与预报潮位水位差异程度。余水位是实测潮位分离天文分潮等可预报潮位之后剩余的部分,其大小受岸线趋势、水域开阔程度、水深、风向、风力及持续时间、气压梯度变化等诸多因素影响。利用实测潮位减去天文潮位等可预报部分的方法实时得到,余水位计算公式为 δ(t)=H(t)-h(t)-△ (3) 式中:δ(t)为t时刻的余水位;H(t)为t时刻实测潮位;h(t)为t时刻的预报潮位值;△为观测误差、计算误差等引起的综合误差,很难量化且数值相对较小,对于采用相同观测方法和相同分析方法的不同站,可认为其△一致,因此统计数据时可以忽略其影响,即余水位为实测潮位与预报潮位的差异值[16]。 表4 各站余水位统计值Tab.4 Statistics of residual water level of each station cm 对CW1~CW3站的余水位进行统计分析(表4),可知该海域的3个潮位观测站的余水位在时间上呈现短周期波动,且各站余水位变化具有高度相关性,余水位变化越剧烈,相关性越强。并且余水位曲线在强烈的增(减)水后有一个小幅度的反弹。增水最大出现在冬季,其次为夏季和春季,秋季最低;减水最大同样出现在冬季,其次为春季和秋季,夏季最低(图3~图6)。从该海域余水位特性和变化规律得出推论:在该海域今后的实际测验作业中,可以通过该余水位增大潮位的测验范围,利用其相关性推算其他站的潮位数据,进而达到减小测验成本的目的。 图3 春季余水位变化过程Fig.3 Hydrograph of residual water level in the spring 图5 秋季余水位变化过程Fig.5 Hydrograph of residual water level in the autumn 图6 冬季余水位变化过程Fig.6 Hydrograph of residual water level in the winter 基于河北黄骅港附近海域三个潮位观测站的四季实测数据,对该海域的潮汐性质、潮位特征值、理论最低潮面、平均海平面、余水位等进行了分析计算。结果表明: (1)黄骅港海域潮汐具有不正规半日潮特性,各测站实测最高潮位夏季最高、冬季最低,实测最大潮差春、夏季大于秋、冬季,平均潮差秋季最大、冬季最小。CW1和CW3站平均涨潮历时小于落潮历时;CW2站涨落潮历时差距不大。 (2)各潮位站每季度的月平均海平面基本一致,各站的月平均海平面均为秋季最高。该海域理论最低潮面值呈现CW2-CW3-CW1逐渐变大的特性,且秋季最高,冬季最低。 (3)该海域余水位呈短周期波动,且各站余水位变化趋势具有高度相关性。增减水最大都出现在冬季。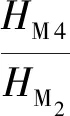
3 潮位特征值


4 平均海平面

5 理论最低潮面
6 余水位特性及变化规律


7 结论
