基于复值损失函数的并行MRI的深度重建

黄进红，周根娇，喻泽峰，胡文玉

赣南师范大学数学与计算机科学学院//江西省数值模拟与仿真技术重点实验室//赣州市计算成像重点实验室，江西 赣州 341000

MRI是断层成像的一种，它利用磁共振现象从人体中获得电磁信号,并重建出人体信息，它的主要缺点是数据采集速度相对较慢。为了解决该问题，研究人员先后尝试了硬件加速、并行成像（pMRI）［1,2］、压缩感知（CS）［3］等方法。卷积神经网络(CNN)已被证明可以为MRI 重建提供快速且稳健的解决方案，很多深度学习模型都包含了CNN模块［4-6］。除了利用CNN网络进行MRI重建，也有作者使用多层感知器网络［7］、编码-解码网络［8］、生成对抗网络（GAN）［9］、递归神经网络［10］等。以上都是基于常规神经网络模块构造的MRI重建模型，这是一种数据驱动的端到端的深度学习重建方法。还有一类称为是基于算法展开（指CS中的相关算法）的深度学习模型，它将传统的求解CS模型过程中每一步迭代转换为神经网络的一个层，根据使用的算法不同构造不同的深度重建模型，如将ADMM 算法展开得到的ADMM-Net 模型［11］，以及将ISTA 算法展开而得到的ISTA-Net模型［12］。

上述大多数深度重建方法将复值MRI数据视为2-通道数据（单线圈）或2c-通道数据（多线圈，其中c表示线圈的数量），从而将数据的实部和虚部分开训练。这种表示方法没有考虑实部和虚部之间的数据相关性，会造成一些相位信息的丢失，从而降低重建精度。针对复值数据，Trabelsi等［13］于2017年提出了专门处理复数的深度网络并应用于计算机视觉领域，取得了较好的定量和定性结果。在MRI重建领域，借助于复梯度计算方法［14］，一种新的适用于复数数据的激活函数［15］，取得了较好的结果。其它MRI应用中的初步研究结果［16-19］也表明了复值神经网络的优势。对于并行磁共振成像领域，利用复卷积运算，提出了一种具有复值输入输出的残差卷积神经网络，用于并行MRI重建，并取得相比于实数卷积网络更好的定量结果，但该方法仅在卷积运算中将相应的实值运算推广到了复数领域［20］。实际上，复数域上的激活函数也引起了部分研究人员的注意。基于深度学习的MRI重建方法时，不仅利用了复卷积运算，还比较了多个适用于复数数据的激活函数对重建精度的影响［21］。

尽管基于复卷积运算、复激活函数的深度重建模型避免了实部和虚部分开训练，提高了重建精度，但损失函数仍采用均方误差（MSE）或平均绝对值误差（MAE），本质上还是对实部和虚部进行了分离。因此，如何设计一种适用于复数的损失函数是一个值得进一步讨论的问题。一方面，对于并行磁共振成像的重建问题，由于涉及多线圈数据，已有方法或者在训练前，或者在训练后，通过“平方和”方法将多线性圈数据合并成单线圈数据。前者在训练前已经丢失相位信息，无法直接利用已采样的多线圈K空间数据，只适合于常规神经网络模块构造的深度重建网络，重建精度相对更低；而后者的网络输出结果是多线圈数据，要得到最终的图像还需进行合并运算，而且这种方法在训练时损失函数是基于多线圈数据计算的，这跟最终需要的合并数据之间的损失函数值并不完全一致。实际上，训练后再合并的方法会导致训练时显示的峰值信噪比（PSNR）较高，而合并后PSNR值明显降低，这是因为合并前是多线圈数据，比合并后的单线圈数据在数量上多了c倍（c表示线圈数量），因此均方误差值有所降低，导致PSNR值增大。另一方面，已有方法在训练时使用的损失函数一般是MSE或MAE，前者是误差平方和的平均数，而后者是误差绝对值的平均数。从统计学角度，这需要以样本间的相互独立性为前提。对于并行磁共振数据，由于不同线圈之间数据噪声并不完全独立，利用MSE或MAE作为损失函数会使估计出的系数产生一定的偏差，导致重建精度有所降低。

基于以上分析，本文提出了基于一种基于复值损失函数的并行磁共振深度重建方法，它相当于在传统网络的基础上增加了一层数据合并层，将多线圈数据合并成单线圈数据，并以合并后的单线圈数据计算损失函数值。该方法既可以充分利用已采样的多线圈K空间数据，又是基于最终需要的合并数据计算损失函数，体现了“端到端”的网络设计。实验表明该方法在定性和定量方面都优于已有的类似方法。

1 方法

1.1 已有复值神经网络的运算模块

已有的复值神经网络主要包括两个区别于实值神经网络的运算模块：复值卷积运算和复值激活函数。

由于并行磁共振图像的自然数据格式是复数，传统方法将其实部和虚部分开作实卷积运算（图1A）。这种方式没有考虑实部数据和虚部之间的耦合性，所以文献［13］中提出利用复卷积运算（图1B）替代这种运算，复卷积运算在后面的很多文献［16-17,21］中也被采纳。用矩阵符号表示，设复数磁共振图像用X表示，卷积核为W，它们的实部分别为Re{X}、Re{W},虚部分别为Im{X}、Im{W}，由于卷积运算具有分布律，故可得：

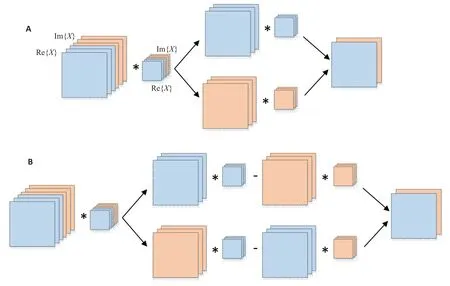
图1 对多通道复值图像的实部和虚部分别作实卷积运算及整体作复卷积运算的区别Fig.1 Depiction of real-valued convolution and complex-valued convolution for multichannel complex-valued MR images.A:Convolution operation applied on real and imaginary parts independently.B:Complex convolution.

对于卷积核的初始化问题，由于在深度MRI重建中一般较少使用批量归一化（Batch normalization），在这种情况下，卷积核这个待训练参数的初始化对克服梯度消失和梯度爆炸问题显得尤为重要［13］。为此我们采用文献［13］中提出的方法，将复卷积核W的初始化分成两步：首先假设W的实部和虚部是独立同分布具有零均值的高斯分布，利用瑞利分布（Rayleigh distribution）对其幅值|W|作初始化；然后利用[-π,π]上的均匀分布初始化W的相位θ，从而得到：

上述瑞利分布中标准差的设定与激活函数有关。若激活函数选择ReLU函数，一般选择He 初始化规则［22］，即σ=，其中nin表示MRI图像的通道数，即并行MRI中线圈的个数。

对于激活函数，在实值深度神经网络中最常用的是ReLU函数，其定义为：

在ReLU函数基础上进行推广，使之适合于复值数据，产生了4 种激活函数：ℂReLU［13］、zReLU［23］、mod ReLU［24］以及心形函数［15］。ℂReLU是ReLU的最直接推广，它直接对复数的实部和虚部作ReLU运算，即：

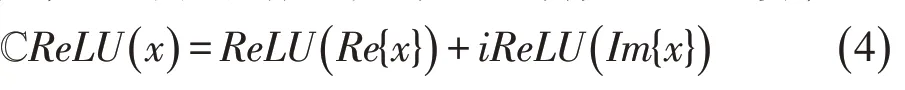
ℂReLU仅在复平面的第一象限和第三象限上满足柯西-黎曼方程（即为解析函数）。与之类似的是zReLU函数，它在第一象限的值不变，其它象限的值为0，并且它在除了实轴正半部分和虚轴正半部分外的复平面上都解析，其定义为：

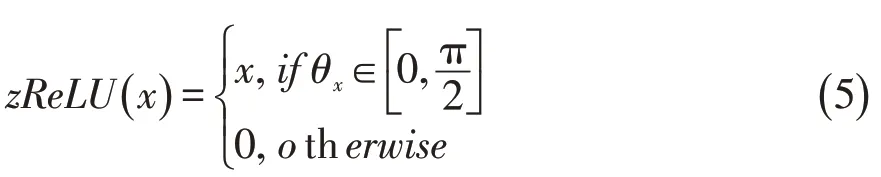
其中θx表示输入变量x的相位。

modReLU中包含了一个可训练的参数b，其定义为：

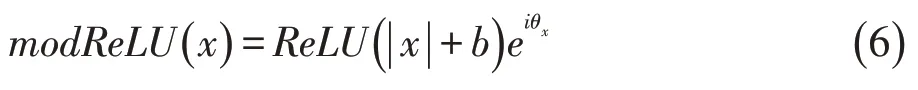
经训练后，b值一般为负值。这个结果导致该函数的函数值除了在原点处为0外，在一个以圆点为圆心、以|b|的半径的圆形区域内也为0；而在该区域外保持相位不变，但幅值增加减少-b。modReLU在整个复平面上都不解析，为了得到一个解析的激活函数，Virtue等［15］提出一个心形激活函数，并用于MRI“指纹成像”中。该函数保持相位不变，但幅值按一定比例缩小，其定义为：

1.2 复值损失函数的构造

对于实值图像，常用的损失函数是MSE或MAE。当我们把复值图像的实部和虚部串联在一起，从而把它看成是实值数据时，已有方法大多选择MSE作为深度学习的损失函数。令训练样本的参考图像为X1,X2,…,XN,其中N表示训练样本个数，通过深度学习网络得到的图像为，它们是在已经网络系数Θ 的前提下，通过网络前向算法得到。为了更新系数Θ，传统方法在训练过程中最小化下面的MSE损失函数：

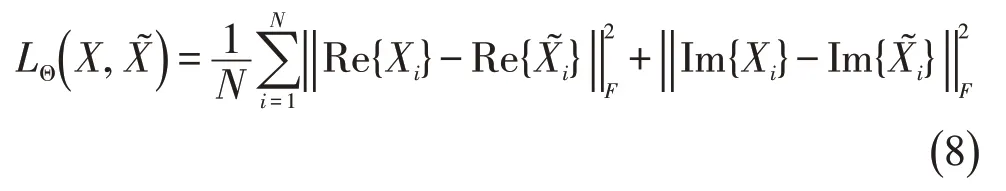
其中‖· ‖F表示矩阵的F范数，即所有元素的平方和的算术平方根。式（8）即为基于MSE的实部和虚部分开计算的损失函数。

从统计学角度看，选择（8）式为损失函数的默认前提是实部和虚部上的噪声是相互独立的，相同位置不同线圈上的噪声也是独立同分布的，前都一般认为是成立的，但后者不太符合并行MRI图像的实际情况。并行MRI图像在同一像素点上不同线圈的原始信号所带噪声是相近的，不能认为相互独立。同时考虑到我们要重建的是一个幅值图像及相位信息，因此，可以先将多线圈数据按照某种方法合并成单线圈数据（一般采用SOS法，即不同线圈幅值的平方和再开方，但这种方法会丢失相位信息），并将式（8）中求和的两部分分别换成幅值和相位，即：

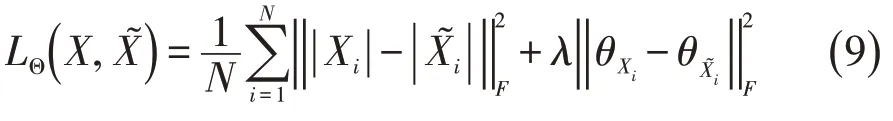
其中|·|表示对矩阵逐元素求模得到的幅值矩阵，θX表示对矩阵逐元素求相位角得到的相位矩阵，参数λ用于平衡幅值方差和相位方差数量级之间的差距。另外，参数λ还可用于调节具体应用中幅值和相位重要性之间的差别，比如在MRI重建中，若只需图像的幅值信息，可设λ=0。在采用SOS法进行合并时，由于此时已经丢弃了相位信息，也需设置λ=0。式（9）即为本文提出的由幅值和相位均方误差构成的复值损失函数。

1.3 基于复值损失函数的深度重建模型

本文利用上述几个基本的神经网络模块，构建一种级联的卷积神经网络［6,20］。如图2A所示，网络主要由卷积模块（CNN）（图2B）、数据一致层（DC）（图2C）以交替方式串联而成，称之为DCCNN网络。首先，将欠采样的K空间数据直接做补零重建，得到具有混叠伪影的图像，并将其作为网络的输入；然后，将其循环往复多次通过卷积子块和数据一致层，最终得到重建图像。

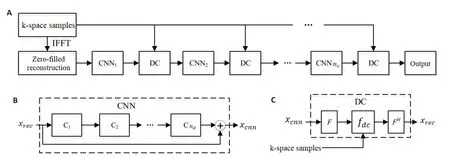
图2 级联卷积神经网络结构图Fig.2 Architecture of the deep cascading CNN.A:The overall design of the network.B:A CNN subnetwork.C:A DC layer of the network.

如图2A所示，网络由nc个模块以串联的方式构成，每个模块由一个卷积子块（含nd个卷积层）和一个数据一致层构成。卷积子块实际上是一个残差网络，学习图像的残差特征，因此具有一定的去伪影和去噪的功能。卷积子块的输出记为xcnn,它等于该子块的输入与学习得到的残差这两项数据之和。随后连同原始的欠采样K空间数据一同输入DC层，其输出xrec等价于求解下面的最小二乘问题：

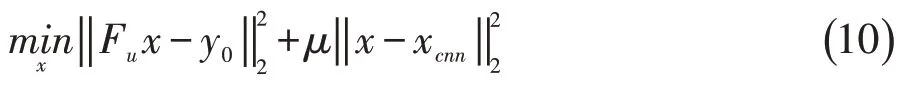
此时我们将待重建图像看成是一个向量x，它在欠采样算子Fu的作用下得到部分K空间数据Fux,它要求尽量靠近原始欠采样数据y0，这由（10）式第一项保证，因此这一项又称为保真项；同时x还不能与上一步CNN子网络得到的xcnn偏离太大，因此需要（10）式的第二项来保证，这一项称为正则化项或先验项（把网络得到的结果看成先验信息）；保真项和正则化项的重要程度通过参数μ来平衡。参数μ一般根据经验取值，在深度学习的框架下，它也可以看作一个待学习的参数，这也是本文的处理方式。

问题（10）虽然是最小二乘问题，但由于像素点多，导致x的维数太大，直接求解不太现实。实际上，根据Fourier变换的性质，问题（10）有一个简单的闭合形式解［6］。令x、xcnn的离散Fourier变换结果分别为y0、ycnn，最优解xrec的离散Fourier变换结果为y，则有：

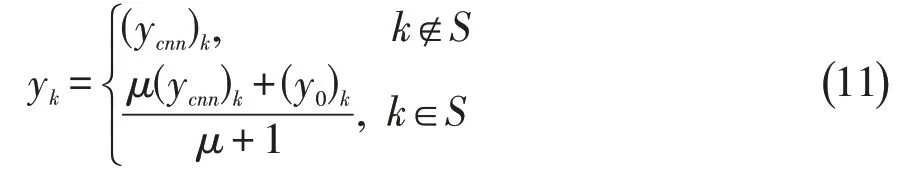
其中S表示采样点位置集合，k表示一个二维采点。求出y后，只需将其作Fourier逆变换即可得DC层的输出xrec，由此便可得到DC层的运算过程，如图2C所示。

1.4 实验数据与采样模式

很多公共数据集提供的是实值MRI图像，通过对实值图像进行Fourier变换得到仿真K空间数据，这样得到的数据集不太符合实际。因此，本文采用公共数据库FastMRI［25］来进行相关实验，它提供了未经处理的全采样K空间复值数据。FastMRI包含两种类型的MRI数据：脑部磁共振图像（Brain MRIs）和膝盖磁共振图像（Knee MRIs）。

Brain MRIs使用包括3T Prisma和1.5T Avanto在内的11种磁共振机型获取了5个临床位置的脑部MR图像，并分成了训练、验证、测试3个数据集。每组MR图像数据是一个多切片、多线圈的四维数组，其中第1维大小表示切片数量（从10到16不等），第2维大小表示线圈个数（从4到20不等），后面两维是图像的空间尺寸，介于640×320及768×396之间。本文收集训练及测试数据时，选取线圈数量为16的数据，对每组这样的数据抽取中间4个切片，并将图像统一裁剪为320×320，这样每个训练数据的维度尺寸为：(16,320,320)。本文实验中一共收集了3334幅这样的16通道图像构成训练数据集，531幅构成验证数据集，120幅构成测试数据集。Brain MRIs中的示例图像如图3A所示。

Knee MRIs中的数据在3个临床3T系统（Siemens Magnetom Skyra、Prisma和Biograph mMR）或1个临床1.5T系统（Siemens Magnetom Aera）中采集，数据采集使用15通道膝关节线圈阵列和纽约大学医学院临床使用的传统笛卡尔2D TSE协议。该数据集的数据来自两个脉冲序列，分别产生带脂肪抑制和不带脂肪抑制的冠状质子密度加权图像。数据采集使用以下序列参数：回波序列长度4，矩阵大小320×320，平面内分辨率0.5 mm×0.5 mm，切片厚度3 mm，切片之间没有间隙。不同系统有不同的重复时间（TR）和回波时间（TE），重复时间2200～3000 ms，回波时间27～34 ms。本文实验中使用的膝盖磁共振图像维数尺寸为（15,320,320），训练数据集、验证数据集、测试数据集中分别包括2519、506、117个样本。Knee MRIs中的示例图像如图3B所示。

本文大部分分实验采用现代商业MRI系统中的等距采样模式，相位编码方向为水平方向，欠采样仅在相位编码方向上进行。空间采样点的位置用一个320×320的mask矩阵来表示，同一组数据不同切面采用相同的mask矩阵。利用mask矩阵从全采样数据中回溯性地掩盖k空间线来执行欠采样操作。利用等距采样模式的所有实验均采用4倍加速，即每隔3条相位编码线进行一次采样，填充矩阵的一列；同时，中间设置24条自校准线，以便应用一些并行成像方法。实验中所用的mask矩阵如图3C所示。

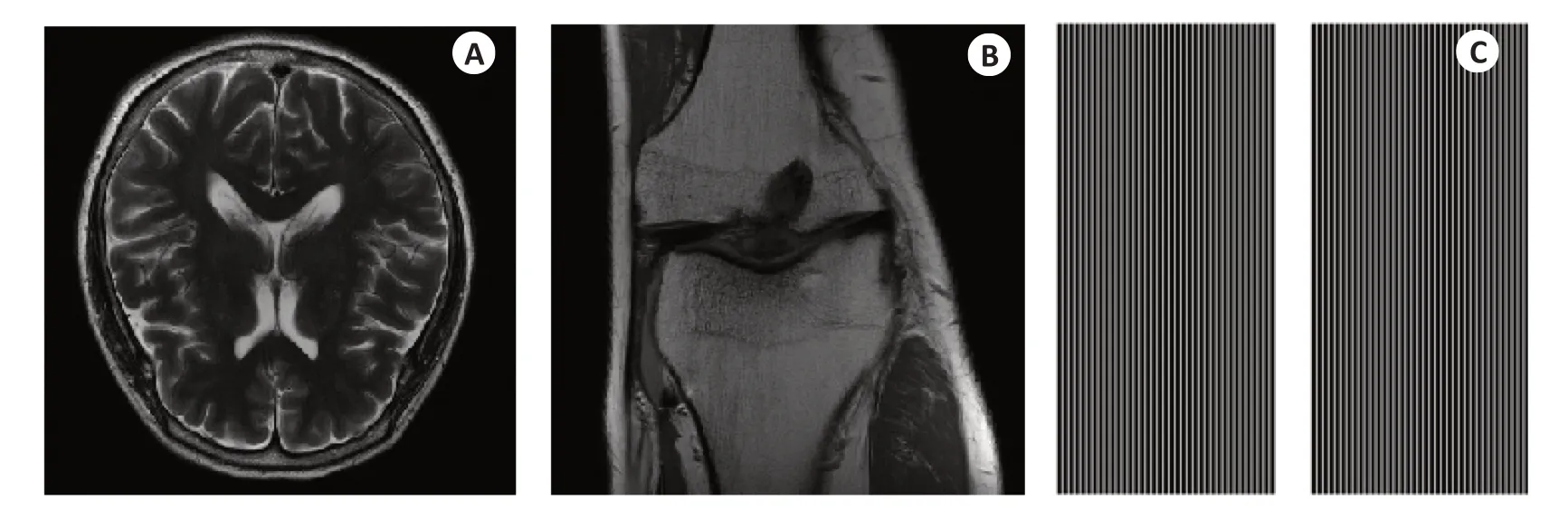
图3 FastMRI中示例图片及4倍欠采样等间隔mask矩阵Fig.3 Representative images in FastMRI and equispaced mask with 4-fold acceleration.A:A brain image taken from the FastMRI dataset.B: A knee image taken from the FastMRI dataset.C: An equispaced mask with an acceleration factor of 4.

1.5 评价标准及网络超参数设定

本文使用峰值信噪比（PSNR）和结构相似指数（SSIM）［26］来度量网络重建图像与全采样重建图像（即参考图像）之间的区别。PSNR 是图像质量评价中常用的度量方法之一，其定义为：，其中Xref表示参考图像，X是待评估图像，MSE是它们之间的均方误差。SSIM根据人类视觉特征评估图像保真度，计算结果位于0和1之间，数值越大，重建结果越好。需要说明的是，本文方法得到的图像其背景部分误差非常小，而其它方法误差相对更大。但是背景区域没有任何图像信息，其误差没有参考价值。为公平起见，本文所有定量结果仅针对前景区域，即去除了背景区域后再计算PSNR值和SSIM值。

在DCCNN 网络中，我们将其规模设定为：nc=5,nd=5,即一共使用5个CNN子模块串联而成，每个CNN子模块包含5个二维卷积层，后面紧跟着一个数据一致层。每个卷积层中卷积核数量均设为32（其参数数量相当于64个卷积核的实值卷积层），卷积核为3×3，滑动窗步长为1，每个CNN子模块中除最后一个卷积层外，都使用由式(4)-(7)定义的某个复值激活函数，最后一层不设置激活函数。每个CNN子模块后紧跟一个数据一致层，该层中有一个待学习的参数μ（见式(10)），其初始值设为200。另外，激活函数ModReLU中也有一个待学习参数b（见式(6)），其初始值设为0。

网络训练过程中使用的优化器选择为Adam，其参数为：β1=0.9，β2=0.99，初始学习率设为0.001，损失函数采用本文中式（9）的形式。由于本文实验只涉及图像重建，不涉及与相位相关的应用，因此式（9）中的λ设为0，即仅以幅值的MSE作为损失函数。训练过程采用小批量训练策略，批量大小为6，最大训练次数设为200，但引入“提前结束”机制，当网络在验证集上的表现在近15次内都没有提升时结束训练。整个训练过程和测试过程均在TensorFlow 2.4平台下完成，设备操作系统版本为CentOS Linux release 7.4.1708(Core)，配备12核Intel(R)Xeon(R)Gold 5118 CPU、128 G内存及2块16GB NVIDIAQuadro P5000 GPU。

2 结果

2.1 不同复值激活函数的实验结果

表1给出了4个不同激活函数分别在脑部数据和膝部数据下的性能表现，表中给出了以不同激活函数训练网络后，对测试数据集进行重建得到的数值均值及方差。从表1中可以看出，modReLU在两个测试集上的数值结果都是最优的，其次是cardioid和CReLU，而zReLU表现最差，几乎与直接补零重建的结果相同。除去zReLU的相关结果，最好的modReLU的结果比最差的CReLU其PSNR值一般高出2 dB左右，SSIM值略高0.01～0.05。由于modReLU的良好表现，后续实验中我们将不加说明地一直使用该激活函数。

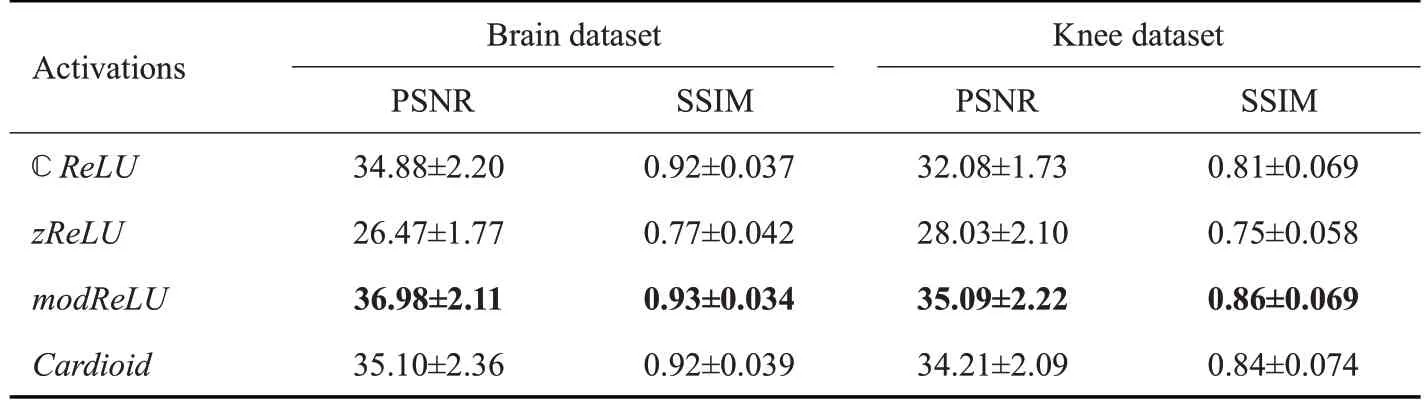
表1 不同复值激活函数的性能比较Table 1 Performance comparison of different complex-valued activation functions

2.2 复值损失函数实验结果

为评价本文提出的复值损失函数对提高重建精度的作用，我们选择3 种性能较好的类似方进行比较：SPIRiT、使用平均绝对值误差作为损失函数的DCCNN（记为L1-DCCNN）、使用均方误差作为损失函数的DCCNN（记为L2-DCCNN），本文的方法记为Mag_DCCNN。图4给出了4种方法对于120组脑部数据的定量重建结果，两幅子图的横轴均为测试数据集中的样本序号，纵轴分别为各样本的PSNR 值和SSIM值。SPIRiT作为一种传统的有效方法，其结果仅作参考，基于深度网络学习的重建方法一般都优于传统方法，从图中也可以明显看出这点。L1-DCCNN已有相关研究［20］，文献中的结论已经证明它是当前最好的模型之一。从图4中可以看出，本文提出的以幅值MSE作为损失函数的方法可以比使用一般损失函数的方法提高精度1 dB左右。

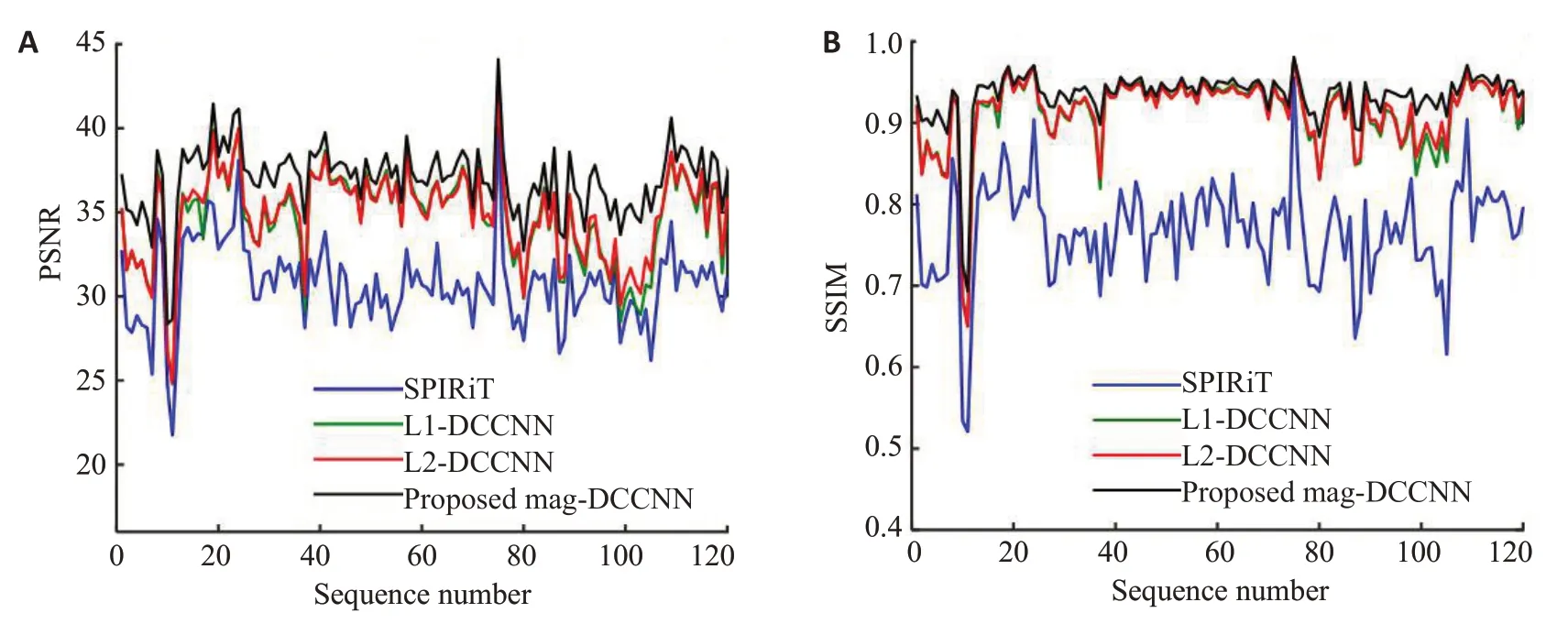
图4 在脑部测试数据集上的定量结果比较Fig.4 Quantitative comparison of the proposed method with other existing state-of-art methods for reconstruction of brain MRI test dedaset. A: PSNR curves for different reconstruction methods. B: SSIM curves for different reconstruction methods.

图5给出其中一组脑部测试数据在4倍欠采样下的定性重建结果，从图中可以看出，3种基于深度学习的方法得到的重建结果均优于传统SPIRiT 方法，Mag_DCCNN给出了精度最高的重建结果。从图像上看，SPIRiT 方法得到的结果存在明显的噪声，而L1-DCCNN和L2-DCCNN的结果上还残留了一些混叠伪影。从定量结果看，L1-DCCNN和L2-DCCNN的重建结果相似，其PSNR值分别为35.76 dB、35.62 dB，而利用Mag_DCCNN 方法得到的重建结果其PSNR 值为36.68 dB；L1-DCCNN 和L2-DCCNN 的重建结果的SSIM值均为0.93，而利用Mag_DCCNN方法得到的重建结果其SSIM值为0.94。

图5 一组脑部试数据经4倍等间隔采样后的重建结果比较，图像下面显示的是PSNR/SSIM值Fig.5 Comparison of reconstruction results using different methods for a brain test dataset with equispaced sampling and an undersampling factor of 4.PSNR and SSIM values are given below the images.

图6给出其中一组膝部测试数据的定性重建结果，和脑部数据实验结果类似，本文提出的Mag_DCCNN方法可以从大量的离线数据集中学习有价值的先验信息，然后对不同MR数据进行高质量的在线图像重建，重建出更多、更清晰的细节。从图片下面的定量结果可以看出，本文提出的Mag_DCCNN方法在PSNR上可以提升1 dB左右，而SSIM仅略微提升。

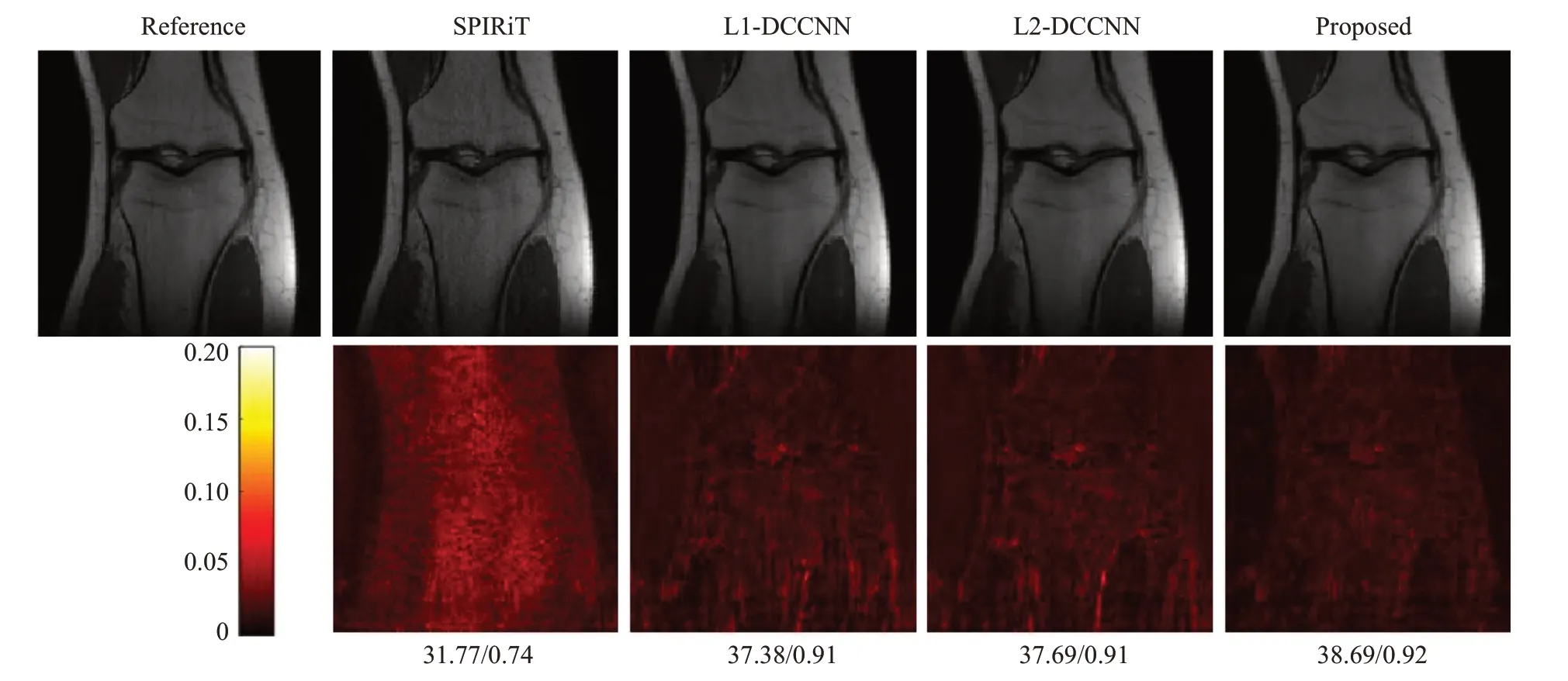
图6 一组膝部试数据经4倍等间隔采样后的重建结果比较，图像下面显示的是PSNR/SSIM值Fig.6 Comparison of reconstructions using different methods on a knee test dataset with equispaced sampling and an undersampling factor of 4.PSNR and SSIM values are given below the images.

为了验证本文所提方法在高欠采样倍数下的有效性，我们在采样倍数设为8的情况下进行了脑部数据的相关实验。由于在高欠采样倍数下，补零重建中含有较严重的混叠伪影，包含SPIRiT在内的传统并行成像方法无法有效去除因欠采样造成的混叠伪影。因此，此实验中我们不再与SPIRiT方法相比，仅比较其它3种方法。为了同时验证方法在不同采样模式下的性能表现，此实验采用二维随机欠采样的模式（图7第1排第2幅子图）。从图7的结果可以看出，3种方法均能有效去除混叠伪影。下方显示的定量结果表明，即使去除没有实际意义的背景部分，本文所提出的Mag_DCCNN得到的重建结果其PSNR 值仍然比L1-DCCNN 和L2-DCCNN的PSNR值略高0.6 dB左右，显示出Mag_DCCNN方法略高的重建精度。

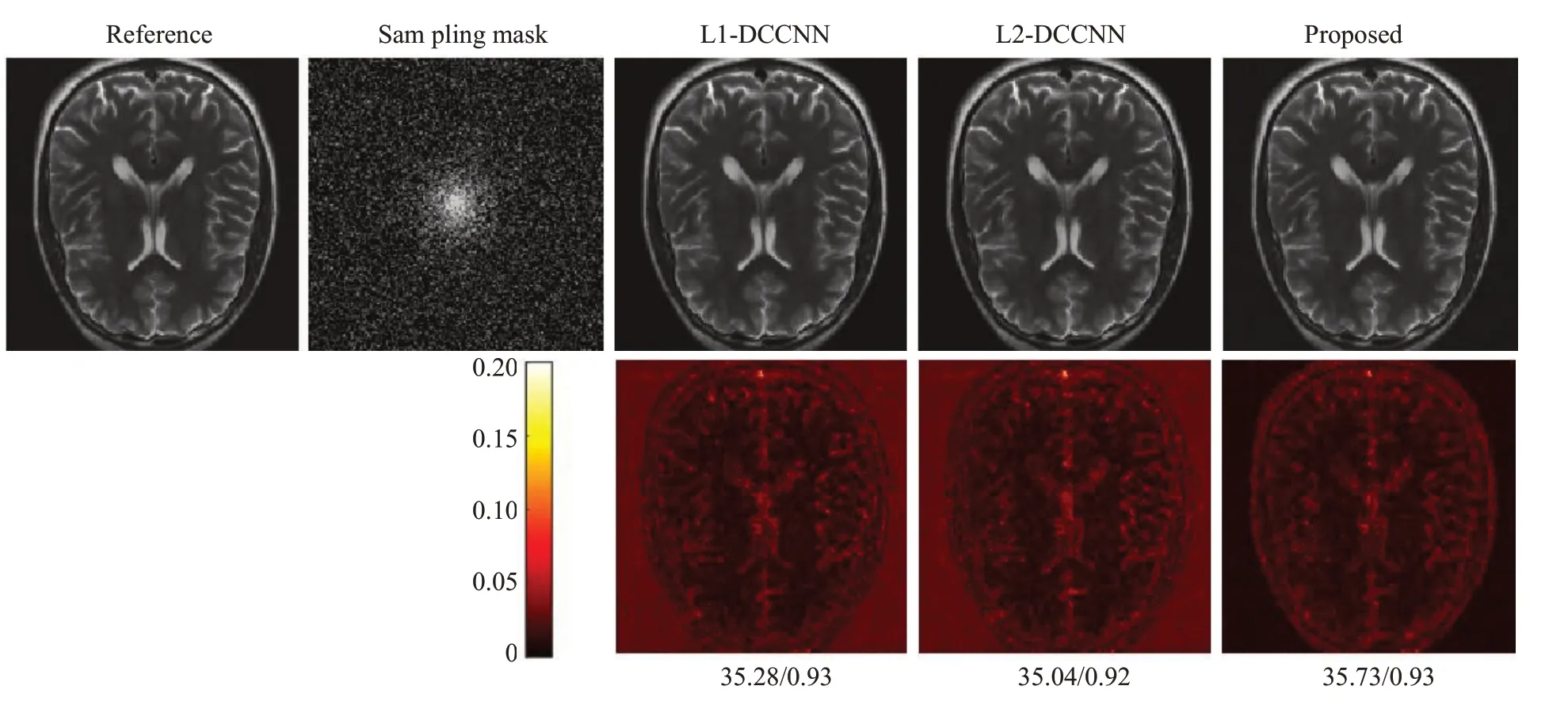
图7 一组脑部试数据经8倍随机欠采样后的重建结果比较，图像下面显示的是PSNR/SSIM值Fig.7 Comparison of reconstructions using different methods on a brain test dataset with 2D random sampling and an undersampling factor of 8.PSNR and SSIM values are given below the images.

2.3 主要参数的设置

文中涉及的主要参数都是参考已有文献进行设置。在网络的深度方面，我们根据文献［6］的研究结果，虽然提高网络的深度有助于精确重建，但考虑到nc＞5、nd＞5 时，训练过程中的内存需求高，同时重建精度提高的幅度明显减弱，因此我们将网络深度确定为nc=5、nd=5，即整个网络包括5个卷积模块，每个卷积模块包含5个卷积层，后面紧跟一个数据一致层。卷积层里的超参数完全按照常规设置，卷积核大小为3×3，滑动窗步长为1，卷积核数量的设置主要还是基于性能和训练难度方面的考虑，设置为32。由于是复卷积核，其实际参数的规模相当于64个卷积核的实值卷积层。在数据一致层中，其计算框架来源于问题（10）的最小二乘求解算法，其中的参数μ虽然是一个可学习的参数，但最后结果显示，经训练之后的μ值变化较小，个别层中几乎相等。这个现象说明μ值初始设置有可能会像压缩感知中的迭代算法一样，在一定程度上影响重建精度。为此，我们针对脑部数据在不同μ初始值的情况下进行了相关实验，实验结果如图8所示。结果表明，当μ初始值在一个较大范围内变化时（10～300），结果的变化并不明显，只是μ初始值过小或过大时，会导致训练提前结束，使得重建结果稍微更差。

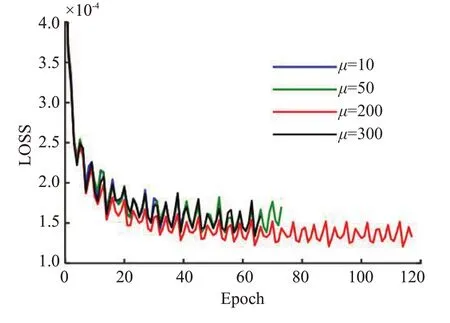
图8 数据一致层中参数μ 的初始设置对网络性能的影响Fig.8 Network performance with different values ofµin data consistency layer using brain dataset.

3 讨论

MRI图像信号包含实部和虚部这两部分的信号，它们分别带有均值为0，方差相同且独立的加性高斯白噪声。但实际中使用的并不是其实部或虚部，而是其幅值函数，因此MRI图像噪声呈Rician分布［27］，在低信噪比位置近似服从瑞利分布，在高信噪比位置近似服从正态分布。已有的基于深度神经网络重建的方法往往对复值多线圈数据的实部和虚部在线圈维度上进行拼接，视为多通道数据，其通道数是线圈数的2倍，并以MSE作为损失函数。从统计学的角度，这相当于使用了正态分布的极大似然估计，而这需要以样本间的相互独立假设为前提。但是，正如前面所述，同一像素点的实部和虚部上的噪声一般认为是相互独立，但同一像素点不同线圈之间的噪声一般不是相互独立。因此，理论上，以MSE作为损失函数的传统方法对单线圈数据是可适用的，但对多线圈数据并不适用。

为了解决上述问题，本文针对多线圈数据，提出了一个新的基于幅值和相位均方误差和为损失函数的图像重建方法。首先，我们按某种方法（如常用的SOS法）将多线圈数据合并成单线圈幅值数据，以消除不同线圈噪声间的相关性，并以此为训练时的标签；同时考虑到在一些应用中相位信息的重要性，因此将损失函数定义为幅值与相位均方误差的和，并用一个参数平衡它们之间的大小。当我们只需要图像时，可以将此参数设为0；当我们只需相位时，可以将其设置为一个充分大的数。在具体实现时，需要在现有的深度学习平台上重新定义损失函数，当然也可以在网络的最后加上一个合并层。合并方法可以采用Walsh等［28］得出的特征向量法（保留相位信息），也可以使用SOS法（丢弃相位），同时将标签数据也按同样的方法进行合并，这样可以方便地使用现有的深度学习平台，如TensorFlow、Pytorch等。实验结果表明，这种方法是有效的，当把平衡参数设为0时，相比于使用常规损失函数，本文提出的方法可以得到精度更高的重建图像。对于涉及相位信息的应用时，此时平衡参数不能设为0，这方面的研究我们将在后续开展。

实卷积神经网络一般采用ReLU函数作为激活函数，即便是采用复卷积的神经网络，有些文献［20］也使用了这类实值函数。为了适合复数运算，有研究者提出在复卷积中使用一些复激活函数，包括：等。关于不同复值激活函数的表现，文献［21］在使用平均绝对值误差（文中称L1损失函数）作为训练时的损失函数的前提下，得出的结论是：ℂReLU表现最好，modReLU表现最差，我们发现这个结论与本文的结果刚好相反。根据本文实验结果，在卷积层使用mod ReLU作为激活函数得到的图像不管在PSNR或SSIM方面都是最好的。出现这种现象的原因是多方面的，但一个重要的原因可能是本文和文献［21］使用了不同的损失函数，文献［21］的损失函数是实部和虚部的MAE之和，而本文采用新提出的幅值MSE作为损失函数。modReLU实际上可以看作是作用在幅值上的ReLU函数，因而它可能更适合于本文的情形。当然，除了损失函数，这种相反的结果还可能与网络结构、训练数据等因素相关。不管怎样，两种结果都反映出一个事实，那就是激活函数对重建结果的影响是不可忽视的，关于具体如何影响重建精度还有待于深入研究。

本文在实验中利用的是真实的脑部和膝部MRI数据，相比于已有文献中多数采用的仿真数据，真实数据的噪声有明显的不同。数据仿真的过程实际上就是对每个线圈上的数据，加入独立同分布的高斯噪声。仿真数据的噪声在实部和虚部之间、不同线圈之间都是相互独立的，因此用MSE作为损失函数可以对相关参数得到很好的估计，从而重建出质量较好的图像。而真实数据的噪声比这复杂得多，分布的类型、独立性都跟仿真数据有较大区别。本文的方法用于真实数据，得到的结果无论是定性方面还是定量方面，都要优于之前的以MSE或MAE为损失函数方法，说明本文所得出的方法更适合于真实数据。

需要指出的是，本文所采用的网络结构中含卷积层，需要事先给定训练数据的通道数，训练数据集中的每个数据样本都必须具有相同的通道数。因此，具有不同线圈数（即通道数）的脑部数据和膝部数据无法放在一起训练，在其中一个数据集上训练好的网络也无法应用于其它数据集，这是本文方法的一个局限性。当然，这同时涉及有关网络扩展性方面的研究，已超出本文的研究范围。

综上所述，本文从统计学角度出发，指出了已有方法的损失函数可能与多线圈MR数据噪声类型不匹配的问题，并针对这个问题，提出了一种简单、可行的处理方法，即先将多线圈数据按照某种方法合并成单线圈数据，然后再以幅值及相位的均方误差为损失函数进行网络训练。合并方法可以选择常规的SOS方法，也可以使用保留相位信息的其他方法。在真实的脑部及膝部数据集上的实验表明这种简单的处理方式是有效的，不管从定性还是定量方面，使用本文提出的方法均优于具有类似结构的用MSE或MAE作为损失函数的相关方法。