拓扑绝缘体中粒子-空穴对称性保护的新奇量子态*
2022-02-03吴亚杰
屠 威,吴亚杰
(西安工业大学 基础学院,西安 710021)
拓扑绝缘体不同于普通的绝缘体,其特殊的能带结构会导致它内部绝缘而边界或表面导电[1-2]。根据拓扑分类,二维体系的拓扑绝缘体可分为两类:破缺时间反演对称性的拓扑绝缘体(陈-绝缘体)和具有时间反演对称性的拓扑绝缘体。陈-绝缘体可通过TKNN拓扑数来标记[3];具有时间反演对称性的拓扑绝缘体可由Z2拓扑不变量来刻画[4-5]。拓扑缺陷(π磁通,位错,涡旋)可以用来探测拓扑材料的拓扑结构,并且材料的拓扑性质和缺陷的拓扑结构相互结合有可能会产生更丰富的物质相。文献[6-7]发现,霍尔丹模型中的π磁通和晶格位错周围会束缚零模态。文献[8-9]发现,在具有粒子-空穴对称性的石墨烯中,点缺陷(格点空位)周围存在零模态。但由于石墨烯无能隙,因此这些零模态(局域态)很脆弱。那么在有能隙的、具有粒子-空穴对称性的拓扑绝缘体中,格点空位周围是否会束缚稳定的零模态,并且如果零模态存在,这些态又具有哪些物理性质,文中正是基于以上思路展开研究。
文中拟建立四方晶格上的拓扑绝缘体模型,加入非拓扑缺陷,根据陈数计算得出模型的相图,并通过对系统哈密顿量的严格对角化得出能级分布及粒子态密度分布。为进一步研究粒子-空穴对称性保护的零模态,拟在体系中加入交错磁场,并缓慢增加格点上的在位势能,得到局域束缚态能量的变化。值得注意的是,文中缺陷周围束缚的零模不能简单当作无能隙边缘态的残留[10]。文中四方晶格上的自旋霍尔丹模型可通过冷原子系统模拟,费米子跳跃过程中获得的相位可利用激光诱导的规范势实现[11-12],利用干涉方法可以探测系统的拓扑不变量-陈数[13]。
1 四方晶格上的无自旋霍尔丹模型
分析第一种拓扑绝缘体(四方晶格上的霍尔丹模型[14]),其哈密顿量描述为
(1)
式中近邻跃迁项为
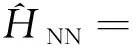
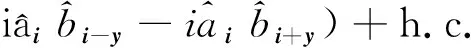
(2)
次近邻跃迁项为

(3)
交错势能项为
(4)
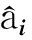
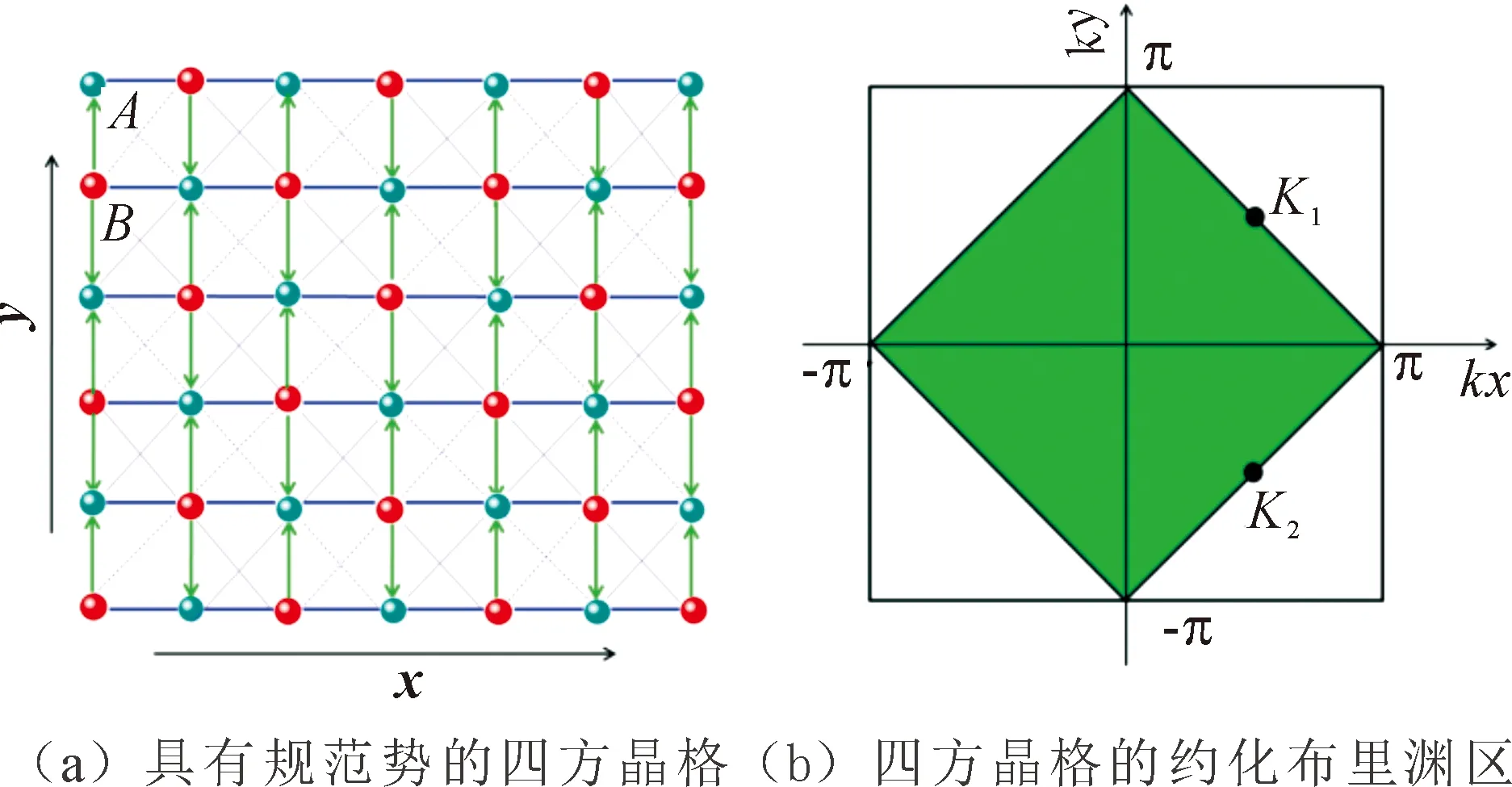
图1 具有规范势的四方晶格模型及其约化布里渊区示意图Fig.1 The illustration of square lattices with gauge potentials and the reduced Brillouin zone
根据傅里叶变换,2个不同子格对应费米算符为
(5)
其中Ns为原胞的个数。经过计算,自由费米子在动量空间的哈密顿量为
(6)
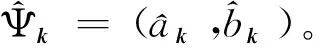
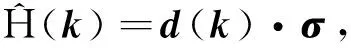
(7)
矢量d(k)=(dx,dy,dz),且
dx=-2tcos(kx),
dy=2tcos(ky),
dz=-2t′[cos(kx+ky)-cos(kx-ky)]-εsp。
(8)
因此,自由费米子的能谱为
(9)
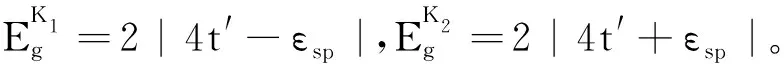
该系统破坏了时间反演对称性,引入陈数来刻画费米子的拓扑性质,即
(10)
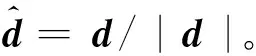
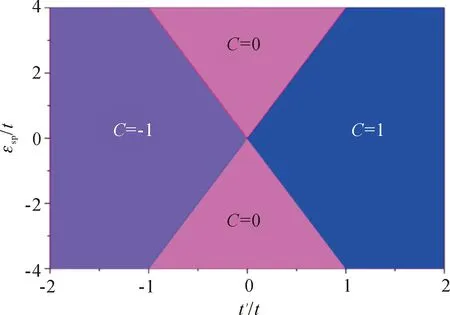
图2 无自旋霍尔丹模型的相图Fig.2 Phase diagram for spinless Haldane model
2 格点空位诱导的零模态

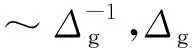
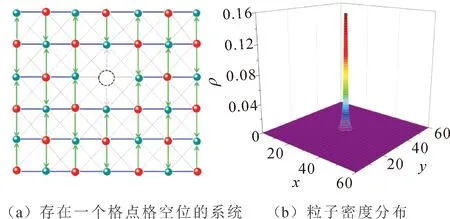
图3 存在一个格点格空位(黑色虚圆圈)的系统及其零模态对应的粒子密度分布的示意图Fig.3 The illustration of one lattice vacancy in the system indicated by dashed circle and the particle density for the zero mode
该零模具有“规范不变性”,当次近邻跃迁系数t′变化时,系统的能隙发生改变,但只要εsp=0,格点空位周围的零模态一直存在,结果如图4(a)所示,红线为局域在格点空位附近的零模态;蓝色区域为连续谱。图4(b)为系统含有一个格点空位时系统的态密度分布,由于诱导零模态的存在,在E=0处出现δ函数峰。图4中所选参数均为t′/t=0.2,εsp/t=0。
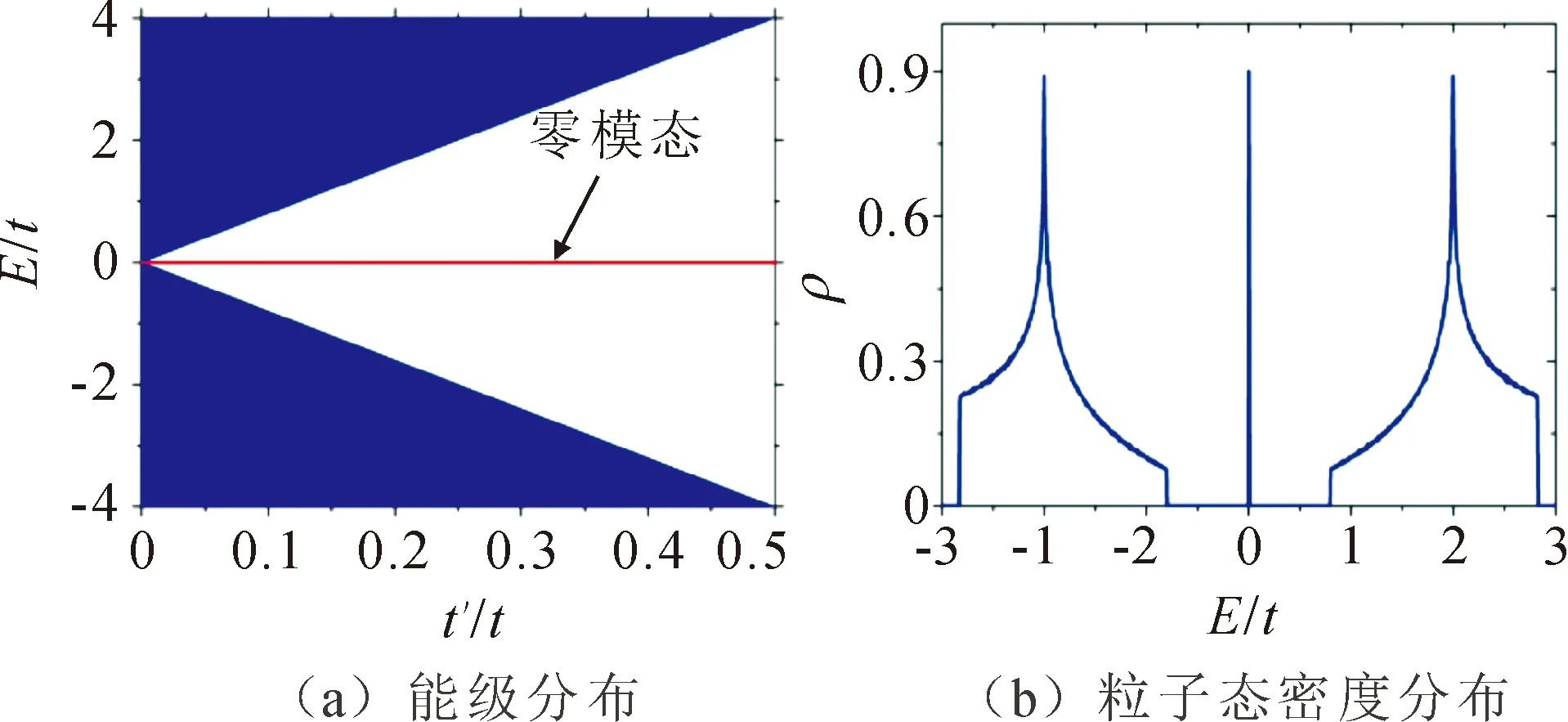
图4 能级分布图和存在一个格点空位时系统的粒子态密度分布图Fig.4 The illustration of energy-level distribution and the plot of particle density for the system with one lattice vacancy
空位缺陷诱导局域零模态具有两类,分别为|+〉和|-〉,其中|+〉为费米占据态, |-〉为费米空占据态。格点空位周围的费米算符为
(11)
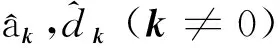
(12)
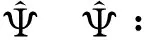
(13)
当系统处于拓扑相时,四方格点上的π磁通作为拓扑缺陷周围同样会诱导一个零模态,它是受拓扑保护的,对任意的局域微扰都是稳定的。该零模态的诱导量子数为±e/2,统计角为π/4,与格点空位诱导的零模态不同。
含有4个格点空位系统如图5(a)所示,当系统存在多个格点空位缺陷时,会出现奇偶效应。当体系中具有奇数个格点空位时(如1个,3个,5个,…),总会有零模局域态存在;而当系统存在偶数个格点空位时(如2个,4个,6个,…),局域态变为有限能量。实际上,体系的粒子-空穴对称性保证了奇数个缺陷情况下零模态及成对束缚态的存在。随着两空位距离的增加,能级劈裂随距离e呈指数衰减。例如,当两个格点空位远离时,两零模态间量子隧穿很弱,能级劈裂很小,系统将存在两个局域的束缚态(准零模态)。含不同格点空位的系统能级分布如图5(b)所示,当t′/t=0.2,εsp=0.0时,包含N个空位时系统的能级分布,红点表示束缚态,当存在奇数个格点空位时,总会存在一个严格的零模态。
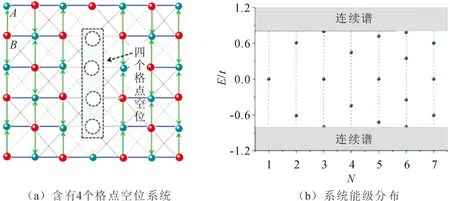
图5 含有4个格点空位系统的示意图和含不同格点空位的系统能级分布图Fig.5 The illustration of the system with 4 lattice vacancies and the distribution of energy levels for the system with different vacancies
3 粒子-空穴对称性破缺的相关分析

缓慢增加格点i0上的在位势能V0,扩展态将逐渐演化为一个局域在格点i0周围的束缚态。当在位势能V0→∞时,束缚态变为严格的零模态。为模拟这一变化过程,将哈密顿量写为
(14)
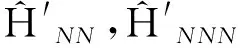
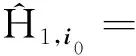
(15)
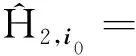
(16)
当在位参数β→0时,在位势能趋于无穷大,此时与格点i0上相关的跃迁项系数全为零,等价于格点i0处存在一个格点空位。当β→1时,系统恢复平移对称性,约化到无格点空位时的情况。通过数值对角化方法,得到β取不同值时的体系能级分布,如图6所示,蓝线表示局域束缚态,所选参数为t′/t=0.2。由图6可知,系统处于拓扑绝缘体相时,任意小的无序势总会导致一个扩展态变为局域的束缚态。
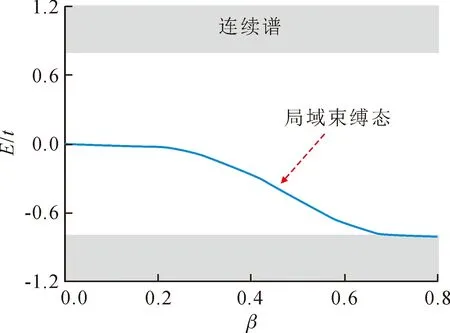
图6 局域束缚态能量随在位参数β的变化示意图Fig.6 The energy of the localized state via the on-site parameter β
4 四方晶格上的自旋霍尔丹模型
自旋霍尔丹模型与无自旋霍尔丹模型相比,该模型含有自旋自由度,并且具有自旋旋转对称性。它的哈密顿量为
(17)
式中近邻跃迁项为
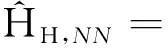
(18)
次近邻跃迁项为

(19)
其中σ=↑,↓分别为自旋向上和自旋向下。运用与分析无自旋霍尔丹模型类似的方法,可以得到自旋霍尔丹模型单格点空位周围会束缚两个零模态,多格点空位情况下同样存在奇偶效应。这些零模态也受到粒子-空穴对称性的保护。
自旋霍尔丹模型中单个格点空位周围的两个束缚态对应四个能量简并态,分别为|↑-〉⊗|↓-〉,|↑-〉⊗|↓+〉,|↑+〉⊗|↓-〉,|↑+〉⊗|↓+〉[17]。在半满情况下,格点空位周围的局域态为|↑-〉⊗|↓+〉,|↑+〉⊗|↓-〉 ,具有1/2磁矩,即
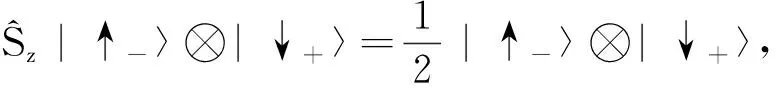
(20)
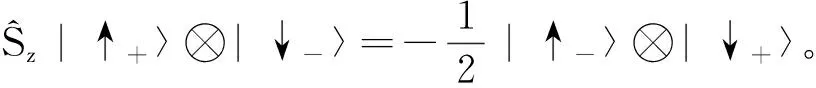
(21)
5 结 论
1) 文中基于无自旋霍尔丹模型和自旋霍尔丹模型,发现非拓扑缺陷(格点空位)会诱导一类新的量子态(零模态),受体系的粒子-空穴对称性保护,它与拓扑缺陷诱导的零模态不同。
2) 在无自旋霍尔丹模型中,单个格点空位诱导的零模态无拓扑构型,但携带e/2分数电荷;在自旋霍尔丹模型中,由于存在自旋自由度,单个格点空位诱导两个零模态,在半满情况下,其携带1/2自旋磁矩。
3) 文中结论具有普适性,对于具有相应对称性的超导或超流系统同样适用。但此时缺陷诱导的束缚态可能对应具有非阿贝尔统计性质的马约拉纳零能态,并具有非平庸的拓扑性质,有待未来进一步深入研究。
