一种改进的加速稳健特征图像配准算法*
2022-02-03冯孝周张文娟
孙 聪,冯孝周,孙 浩 ,张文娟
(1.西安工业大学 基础学院,西安 710021;2.中国兵器工业集团公司测试研究院,华阴 714200)
图像配准作为一种重要的图像处理技术,已经广泛应用于模式识别、医学图像处理、计算机视觉、毁伤评估、图像拼接、目标检测等领域[1-3]。图像配准是将不同时间、不同传感器、不同角度等条件下拍摄的两幅图像实现几何校正的过程[4]。不同的图像配准算法,配准原理并不相同,主要可以分为基于灰度的图像配准算法和基于特征的图像配准算法。基于灰度的图像配准算法主要通过待配准图像与参考图像的相似灰度值点进行配准,比较容易实现,但配准精度不高[5-6]。而基于特征的图像配准算法鲁棒性较好,且具有较高的配准精度,是目前应用较为广泛的图像配准算法[7-8]。
尺度不变特征变换(Scale-Invariant Feature Transform,SIFT)算法是基于特征分析的图像配准算法,该算法具有完整的尺度不变性,但其算法的实现过程比较复杂且实时性不高。针对SIFT算法的不足,文献[9]对SIFT算法进行改进,提出了加速稳健特征(Speeded Up Robust Features,SURF)算法,相较于SIFT算法其在特征点的提取速度上快3倍左右,提高了匹配速度和配准精度,但对于仿射角度较大的图像配准方面,SURF算法配准精度不高。为了使图像配准具有实时性,文献[10]提出了一种快速特征点提取和描述(Oriented Fast and Rotated BRIEF,ORB)算法,其采用二进制特征描述符,理论计算速度约为SIFT算法的100倍左右,实时性远优于SIFT算法和SURF算法,但其配准精度不高。传统的ORB算法在尺度变换鲁棒性和特征点主方向选取方面均不如SURF算法。
近年来许多学者对SURF算法进行了改进,在特征点对的提取和筛选方面,文献[11]在SURF算法的基础上采用分割圆形区域提取描述符,能够减少计算量,但该方法采集到的特征点相对较少且分布集中。文献[12]采用随机采样一致性(Random Sample Consensus,RANSAC)算法进行特征点精匹配,可以得到稳健性较高的正确匹配,但运行时间稍长。文献[13]通过使用Hessian矩阵检测特征点对,并使用最近邻与次近邻的比值来筛除错误匹配点,该算法配准效率较高,但配准精度有待提高。文献[14]采用快速最近邻搜索包(Fast Library for Approximate Nearest Neighbors,FLANN)算法对特征点进行匹配,提高了匹配正确率,但对于大角度仿射图像难以做到精确配准。在特征点的描述方面,文献[15-18]按照主方向选取正方形区域,计算区域内水平和垂直方向上的小波响应,并赋予响应值权值系数,以此来形成描述向量,但计算较为复杂,耗时较长。文献[19]对SURF算法的描述符进行了改进,并采用RANSAC算法筛除误匹配,有效提高了点对的正确匹配率,但该方法需要较大的计算代价。
基于此,针对SURF算法存在的计算复杂、实时性低、配准精度不高等不足,文中拟提出一种改进的SURF配准算法,该算法使用BRIEF描述子对特征点进行描述,误匹配的筛选方面通过改进的随机一致性抽样算法实现匹配点对的提纯,最终计算出单应性矩阵,并应用于待配准图像。基于二进制的BRIEF描述子和改进的RANSAC算法的加入,能够在保证精度的同时提高运行速度。
1 算法的改进与实现
改进的SURF配准算法,通过构建尺度空间筛选出稳定的特征点,根据筛选出的特征点与周围像素点灰度值的比较,生成二进制的BRIEF描述子对特征点进行描述,由于该描述子维度较高,在特征点匹配阶段可降低噪声的干扰风险,并加入旋转矩阵使描述子具备旋转不变性。由于使用了二进制描述子,文中基于汉明距离采用K最邻近法(K-Nearest Neighbour,KNN)算法进行特征点粗匹配,并通过调节最近邻特征点与次近邻特征点的汉明距离比值进行粗筛选,粗筛选后仍然会存在部分误匹配点,为了进一步提高配准精度,使用改进后的RANSAC算法进行提纯。计算出单应矩阵,并应用于待配准图像,实现配准过程。
1.1 特征点检测
1.1.1 构建尺度空间
在特征点检测过程中,为了使其具备尺度不变性,需要在不同尺度下检测特征点。图像的大小总是不变的,采用不断增大滤波模板尺寸的间接方法。在相同组内的图像层之间使用相同大小的滤波器,但这些滤波器的模糊程度在组内将逐渐增大。不同尺度的图像涵盖的信息特征不同,低尺度的图像细节更加清晰,高尺度的图像抗噪能力更强。在各个尺度下均达到Hessian矩阵极大值的点确定为特征点。
通过变换滤波器的大小来实现图像的尺度变换,变化过程中生成的图像金字塔即为尺度空间。图1表示第1—2组滤波器尺寸变化图。图1中随着尺度的增大,被检测到的斑点数量迅速衰减,因此,一般进行3—4组。
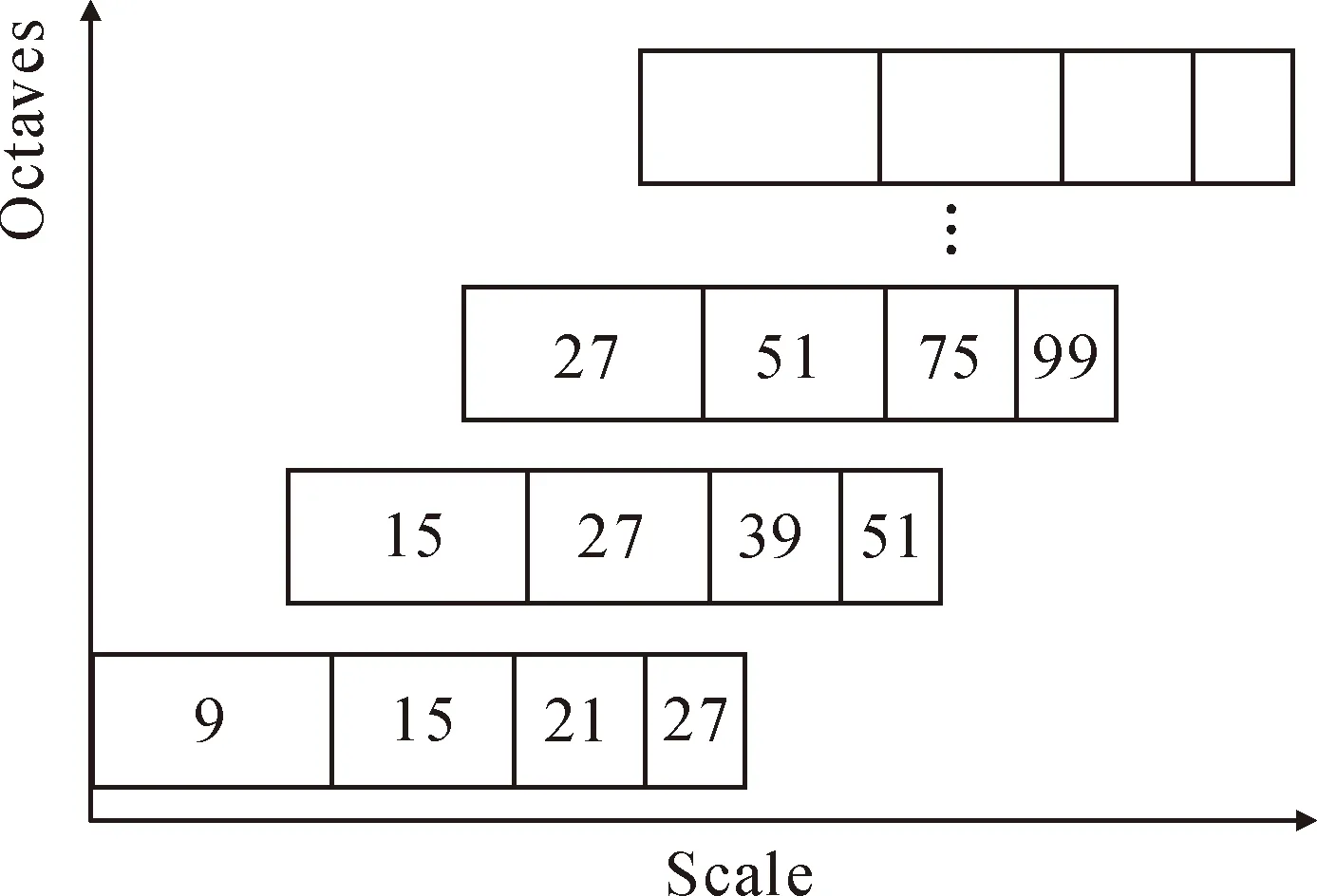
图1 尺度变化图Fig.1 Variation in scale
1.1.2 特征点检测
特征点检测的核心思想是尺度空间理论。若图像M内任意像素点表示为M(x,y),那么尺度是σ的Hessian矩阵H(m,σ)描述为
(1)
式中:Dxx(m,σ)为图像M中点m与高斯二阶滤波∂2g(σ)/∂(m2)的卷积,其余参数表示含义与Dxx(m,σ)相似,进而求解Hessian矩阵为
Det(H)=DxxDyx-(ωDxy)2>K,
(2)
式中:K为选定的阈值;ω为补偿系数。当Hessian矩阵在图像的某一像素点的值大于阀值时,可以判定当前像素点为关键位置点。最后在尺度空间和图像空间中使用差值法来精确定位特征点。
1.2 生成BRIEF特征描述
BRIEF作为一种二进制的特征描述符。它是在每一个特征点的邻域内,选择n对像素点,与选择的像素点灰度值进行比较。其思想是在关键点的邻域用较少的灰度值对比来对特征点进行描述。定义一个准则
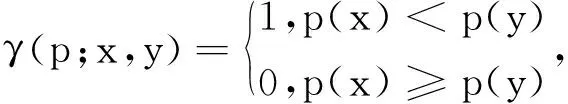
(3)
式中:p(x)为关键点邻域的点灰度值;点对(x,y)为根据高斯分布所选的点对,n个这样的点对组成了n维二进制描述子,一般n取128,256。即
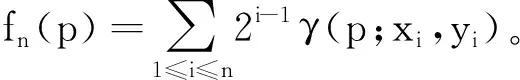
(4)
由于BRIEF描述子由特征点邻域n个点对生成,不具备旋转性,当待配准图像与参考图像的畸变角度过大时,配准效果不佳。为了使其具备旋转不变性,将这n个点组成矩阵S为
(5)
使用邻域方向θ和对应的旋转矩阵Rθ,构建的一个修正版本Sθ:
Sθ=RθS。
(6)
则生成了具有旋转不变性的描述子,即把坐标轴旋转一定角度,计算以特征点主方向为坐标系的匹配点对均具有方向一致性。
1.3 特征的匹配与筛选
1.3.1 特征点粗匹配
使用汉明距离对特征点描述子的相似性进行度量,参考图像特征点与待配准图像特征点间的汉明距离越小,则这两个特征点的匹配度越高,反之越低。采用KNN算法进行特征点的粗匹配。虽然修正后的BRIEF具有较强的分辨能力,但是仍然会出现错误匹配的情况。
参考图像和待配准图像的特征点描述子分别是q=(q1,q2,…,qn),p=(p1,p2,…,pn),计算q中每个描述子和p中所有描述子的汉明距离,并进行从小到大排序,按照式(7)计算比值,dj1和dj2分别为最近和次近点间的汉明距离,该值反应最近点与次近点的关系,当这个值具有更大差异优势时才能构成匹配点,通过设置阈值τ可以剔除一部分错误匹配点。
(7)
当τ设置的较大时,就会获得较多的匹配点,当τ设置的较小时,会导致匹配点不足,影响单应性矩阵的计算,因此不同的图像需要设置不同的τ值。图2为特征点粗匹配结果。

图2 特征点粗匹配Fig.2 Rough matching results of feature points
从图2可以看出,匹配图中存在部分误匹配点对,这些误匹配点如果不能得到有效剔除会影响图像的配准精度。进一步观察发现,误匹配点对的连线角度和正确匹配点连线角度差距较大,这也对算法改进提供了思路。
1.3.2 RANSAC算法的改进
粗匹配后的点对中存在不少错误匹配点,影响单应矩阵的计算,进而影响图像配准精度。由此文中采用几何约束算法对RANSAC算法进行改进,实现对特征点对的提纯。
待配准图像与参考图像之间,正确匹配点之间的连线基本平行,其夹角在一定范围内,如果存在错误匹配点,其夹角则不在此范围内。利用这个特点可剔除一些不满足要求的匹配点。在上一步粗筛选后,特征点连线的角度βi,计算出其平均角度βmean。
(8)
正确的特征点对连线角度应该在βmean上下波动,若连线角度与相差较大,则会被认为是错误的特征点对。
随机一致性抽样算法需要迭代的次数较多,为了缩短算法耗时,改进的随机一致性抽样算法步骤为
① 随机从数据集中随机抽出4个样本数据(此4个样本之间不能共线),计算出单应矩阵H,记为模型m。
② 利用几何约束法对剩余特征点进行约束,对大于βmean的特征点对进行剔除,减少计算时间。
广垦畜牧旗下广东红马饲料有限公司年产饲料达50万吨,广东广垦恒之康食品有限公司和东莞市广垦食品有限公司开拓了生猪销售终端市场,“黑加宝”黑土猪优质猪肉专卖店在广州、深圳、东莞达400家。集团还与美国、澳洲、欧洲(丹、法、德、荷)等国外同行合作密切,积极实施“走出去”战略,进一步拓展广垦畜牧海外发展业务。
③ 计算剩余特征点与模型M的投影误差,若误差小于阈值,加入内点集I。
④ 若当前内点集中特征点数大于最优内点集中的数目,则认为当前参数模型矩阵为最佳矩阵。
⑤ 直到内部点数趋于稳定,计算最终的变换矩阵。
改进的算法由于初始样本集合中内点数增大,能有效减少了算法的迭代次数,节约算法耗时。通过改进的算进进行匹配点对提纯,结果如图3所示。

图3 提纯后的匹配点对Fig.3 Purified matching point pairs
从图3中可以看出,改进的算法能够有效地筛除误匹配点,经过提纯后,匹配点间的连线角度,基本在一个很小的范围内波动。
2 实验结果与分析
实验选择4组图像进行配准验证,结果如图4所示,左边图像设为参考图像,右边图像设为待配准图像,来进行配准实验。其中A、B组图像大小为512 pixel×512 pixel、C组图像大小为341 pixel×341 pixel,D组图像大小为2 048 pixel×2 048 pixel。

图4 实验对象Fig.4 Experimental subjects
图4中B组图像是在A组图像的基础上加了均值为0,方差为10的高斯噪声,C组图像为大角度旋转,D组图像检测配准算法的仿射变换处理能力。对比不同配准算法的配准效果和配准时间,对改进的配准算法做出科学的评价。将SURF图像配准算法和ORB图像配准方法作为参照,不同配准方法的配准耗时对比如图5所示。
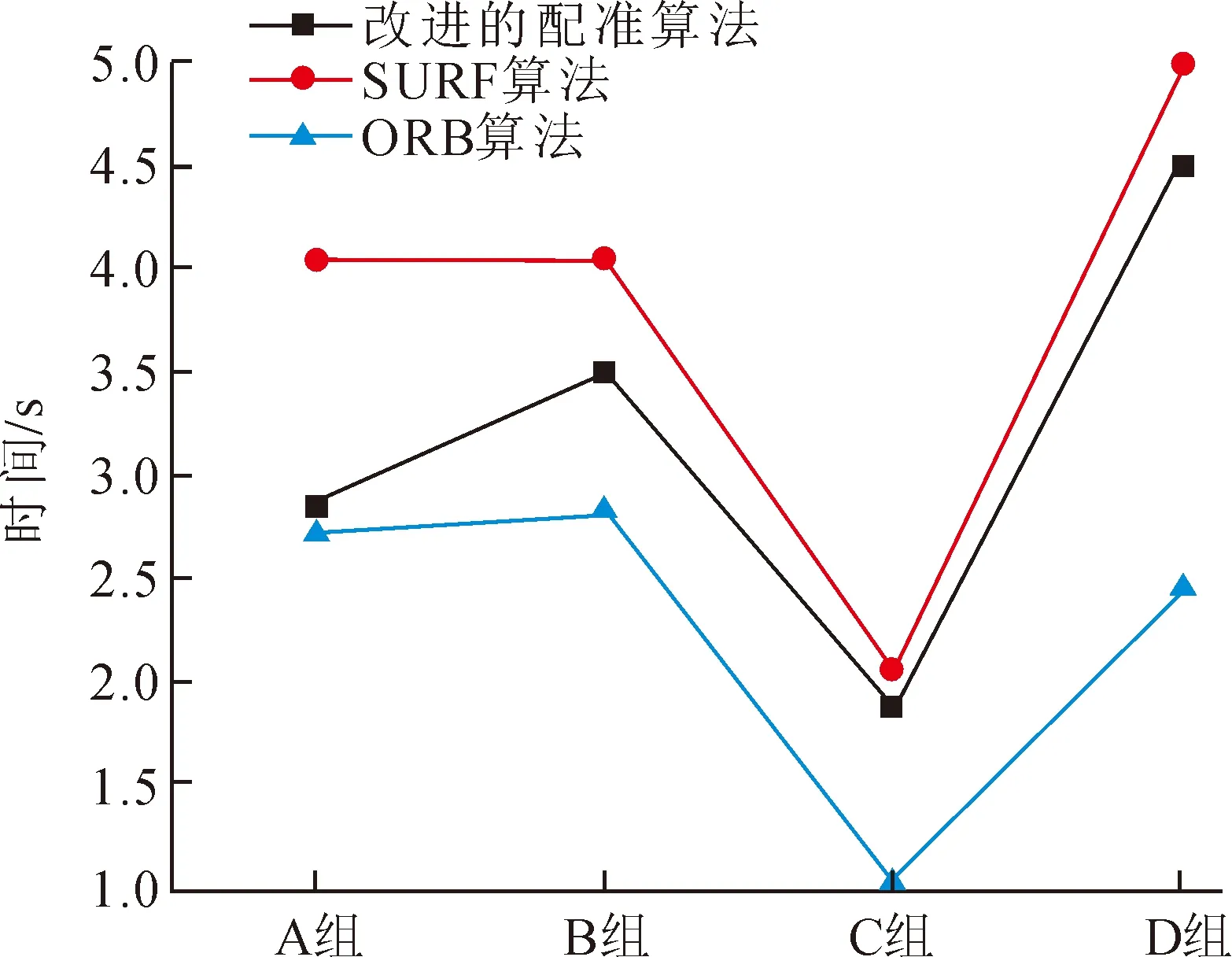
图5 配准耗时对比图Fig.5 Contrast of alignment time consumption
从图5可看出,改进后的图像配准算法耗时明显低于SURF配准算法,经计算平均降低了16%,但相较于ORB图像配准算法仍有很大的进步空间。
不同配准方法的配准偏移对比如图6所示。
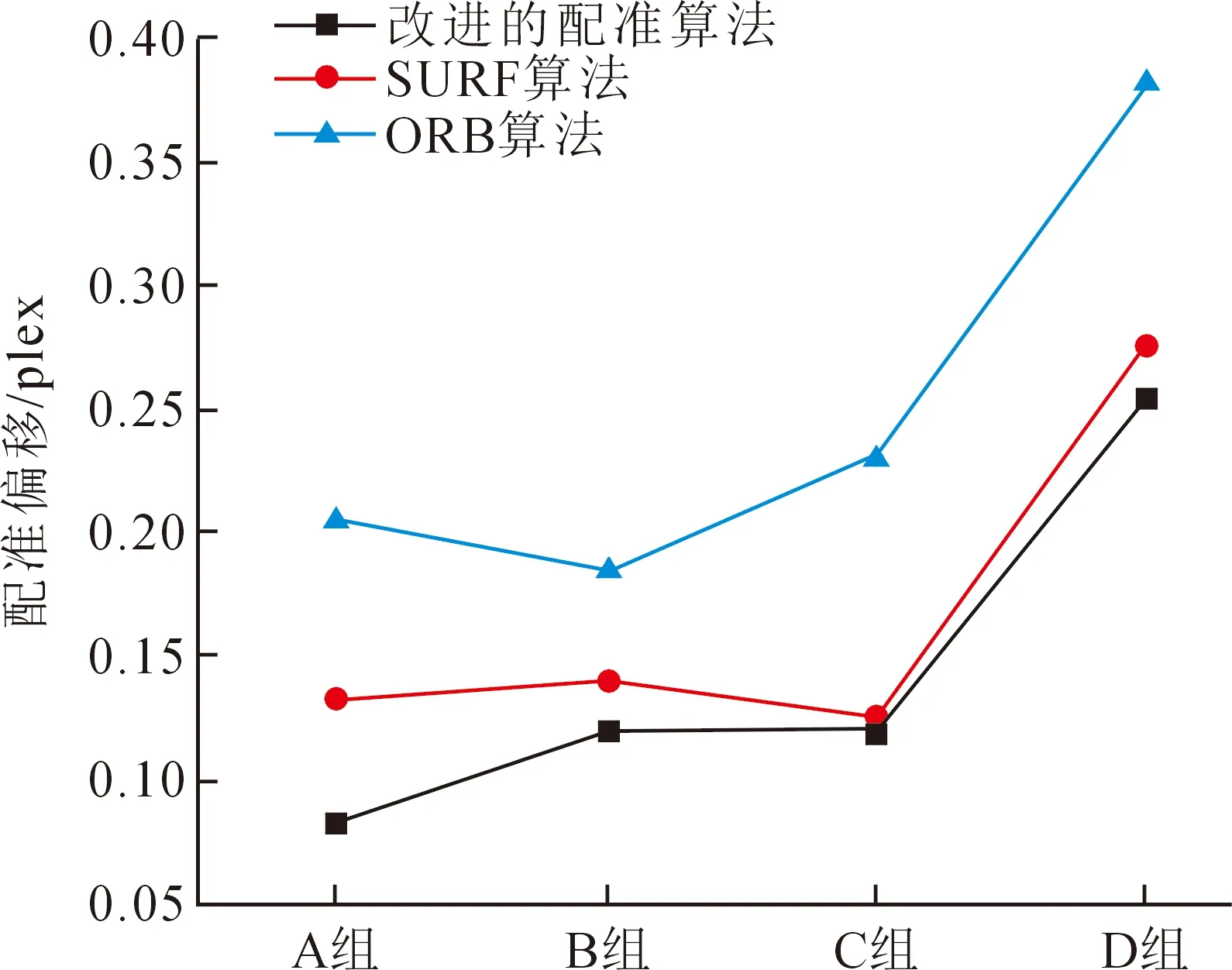
图6 配准偏移对比图Fig.6 Contrast of alignment offset
相比于SURF算法和ORB算法,改进后的图像配准算法能够较好的兼顾噪声、大角度偏移、仿射变换等环境下的图像配准,噪声环境下对比于SURF算法,配准偏移下降了13.8%取得了良好的配准效果。
综合图5和图6,文中的算法虽然在配准效率方面略低于ORB算法,但在配准精度方面较SURF和ORB算法具有较大优势。仿真结果如图7所示。

图7 不同图像配准方法的实验结果Fig.7 Experimental results obtained by different image alignment methods
从配准结果图可以直观的看出对于噪声图像和仿射变换图像,ORB算法不能很好的完成配准,配准后的实验数据产生了明显的变形,无法实现有效配准。经过SURF算法和文中算法配准后的图像主观效果良好,实现图像空间位置的一致性调整。仿真实验过程中得到的具体配准偏移误差和完成配准所消耗的时间见表1。
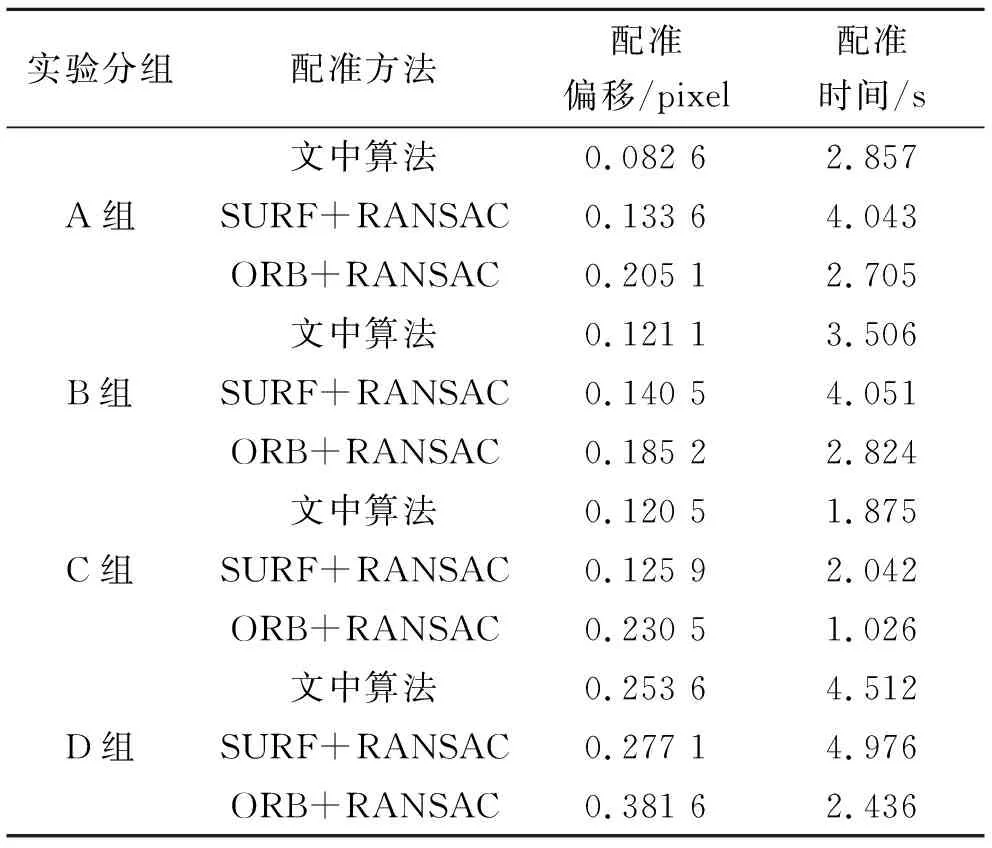
表1 不同图像配准方法的实验结果Tab.1 Experimental results obtained by different image alignment methods
对实验过程中得到的配准时间与配准偏移进行综合分析可得:ORB 配准算法虽然配准耗时最少,但配准误差较大;SURF配准算法虽然在精度方面优于ORB算法,但实时性较低。文中提出的配准算法融合了两种算法的优点,噪声环境下的配准偏移仅为0.121 1 pixel,四组图像的平均配准偏移为0.144 pixel,平均配准耗时为3.187 5 s,相比于SURF算法无论是配准精度还是运算耗时方面,均有较大优势。
3 结 论
1) 针对SURF配准算法在实际应用中存在计算复杂、配准精度不高、鲁棒性差等不足,文中提出了一种改进的SURF图像配准算法,主要在特征点描述和误匹配点对的筛选方面进行了优化。采用二进制高维描述子对特征点进行描述,一方面对特征点进行精确描述的同时降低了噪声的干扰,另一方面得益于二进制的高速运算也提高了算法运行速度。误匹配点对的筛选方面通过几何约束算法对RANSAN算法进行了改进,增大了初始样本集合中的内点数,从而减少算法的迭代次数,最终高效筛除了误匹配点,提高了配准精度。
2) 设置不同环境下的图像来测试文中算法的配准效果,实验结果表明:文中的配准算法相较于SURF配准算法,在噪声环境下配准偏移降低了13.8%,四组实验中配准偏移平均降低了14.7%,配准总时间平均降低了15.63%,无论在配准精度还是配准效率方面均取得较好的效果。
