构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略

胡宇飞，田 震，查晓明，孙建军，李翼翔，万子镜

（武汉大学电气与自动化学院,湖北省武汉市 430072）

0 引言

随着风电、光伏等可再生能源的高速发展,作为新能源并网重要接口的电力电子变流器在电力系统中的渗透率不断提高,现代电力系统的发展逐渐呈现出高比例可再生能源和高比例电力电子设备的趋势［1-3］。微网作为实现新能源分布式接入与灵活组网的重要方式之一,包含了动态特性各异的多样化电源［4］。在以分布式电源为主体的交流微网系统中,由于缺少同步发电机提供惯量和阻尼支撑,容易出现系统频率稳定性问题［5］。

目前,交流微网系统中的新能源并网逆变器大多为跟网型变流器（grid-following converter）,其外特性表现为电流源,通过直接控制输出电流,能够实现分布式电源的高效利用,但是缺乏频率和电压支撑能力［6］。为了解决微网系统缺少惯量、阻尼较弱的问题,国内外学者提出了多种构网型变流器（gridforming converter）控制策略［7-8］,使得逆变器能够模拟同步发电机的惯量和阻尼特性,为系统提供稳定的频率支撑。文献［9-10］基于阻抗分析法比较了电压控制型虚拟同步发电机（virtual synchronous generator,VSG）、电流控制型VSG 以及传统并网逆变器的并网特性,指出电压控制型VSG 对弱电网的适应性更强。文献［11］基于特征值分析法指出投入构网型逆变器能够等效提高电网强度,增加跟网型逆变器的稳定性。

目前,大部分文献仅关注单一类型逆变器在弱电网条件下的并网稳定性。文献［12］基于谐振模态分析法分析了多跟网型逆变器并网稳定性,以及逆变器参数、线路阻抗等因素的影响。文献［13］基于特征值分析法分析了多VSG 并联系统的稳定性,结合特征值运动轨迹研究了不同参数对系统稳定性的影响。文献［14］在dq旋转坐标系下建立了跟网型逆变器的阻抗模型,分析了微网系统中并联逆变器与电网的谐波交互问题。对于同时含有构网型逆变器和跟网型逆变器的孤岛微网系统稳定性分析,目前尚不多见。

另外,现有文献大多是在固定稳态工作点下进行小信号建模分析,主要关注逆变器控制参数以及电网强度对系统稳定性的影响,缺少对系统稳态工作点影响的深入研究。而对于以电力电子变流器为主导的孤岛微网系统,系统稳态工作点的变化将改变逆变器的动态特性,从而显著影响孤岛微网系统的稳定性。

谐波线性化方法最初被用于研究单相功率因数变换器的阻抗模型［15］,随后文献［16］采用谐波线性化建立了电流控制型并网逆变器的序阻抗模型,文献［17］基于阻抗稳定性判据,分析了逆变器并网稳定性。相较于dq阻抗建模方法,基于谐波线性化方法建立的序阻抗模型具有正负序解耦、物理意义清晰、稳定判据简洁明了、多机系统中无须额外考虑坐标系变换等优点［18-21］。文献［9-10］基于谐波线性化建立了VSG 的序阻抗模型,但是忽略了滤波电路、无功环路和控制延时的影响,可能导致系统稳定性结果的误判。

本文针对无电网支撑、逆变器主导的孤岛微网系统,首先,采用谐波线性化建立了考虑无功环路及控制延时影响的序阻抗模型,分析了系统参数及逆变器功率分配对系统稳态工作点的影响,探究了在宽范围工况下不同系统参数及逆变器控制参数对系统阻抗稳定性的影响规律。其次,在计算系统稳定参数边界的基础上,本文提出了一种适应系统工况变化的虚拟阻抗设计方法,显著提高了孤岛微网系统的稳定性。最后,利用仿真和实验验证了本文阻抗分析和虚拟阻抗控制的有效性。

1 孤岛微网系统序阻抗建模

1.1 孤岛微网系统主电路结构

本文研究的孤岛微网系统的主电路拓扑如图1所示,构网型逆变器和跟网型逆变器经过联络线在公共连接点（point of common coupling,PCC）并联,并同时为PCC 处负载Zload供电,其中:构网型逆变器采用电压控制型VSG 控制策略；跟网型逆变器采用电流前馈解耦控制策略,通过锁相环与构网型逆变器保持同步。

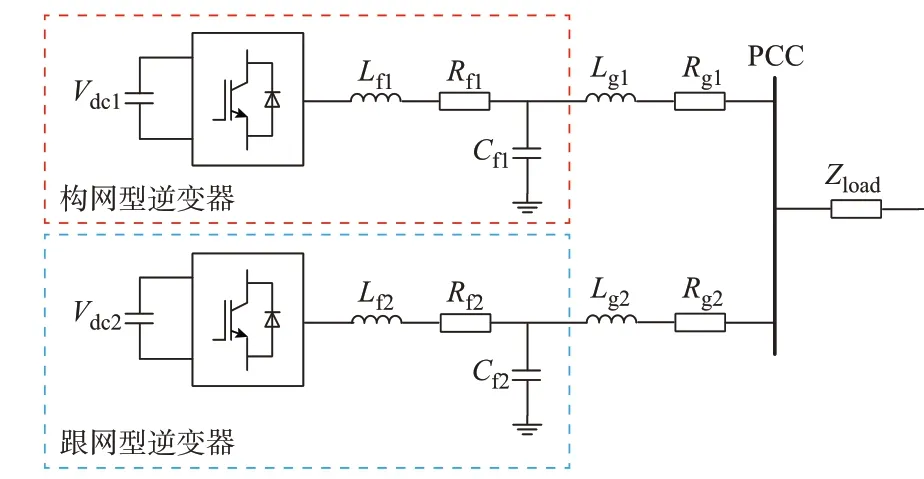
图1 孤岛微网系统主电路拓扑Fig.1 Main circuit topology of islanded microgrid system

图1 中:下标1、2 分别代表构网型和跟网型逆变器；Vdc1和Vdc2分别为构网型和跟网型逆变器直流侧母线电压；Rf1、Lf1、Cf1和Rf2、Lf2、Cf2分别为构网型和跟网型逆变器的滤波电阻、电感和电容；Rg1、Lg1和Rg2、Lg2分别为构网型和跟网型逆变器的联络线电阻、电感。系统电路参数、构网型及跟网型逆变器的控制参数分别如附录A 表A1、表A2、表A3所示。

1.2 基于VSG 控制的构网型逆变器

VSG 以传统同步电机的转子运动方程作为控制内核,模拟传统同步电机的动态特性和同步机制,从而向电网提供惯性和阻尼［9-10］。典型VSG 的主电路拓扑如附录A 图A1（a）所示［9-10］,其中:Vdc为直流侧母线电压,可以认为是稳定值；ea、eb和ec为VSG的三相桥臂电势；ema、emb和emc为VSG 控制回路的三相调制波；Tde为控制延时；va、vb、vc和ia、ib、ic分别为VSG 的 输 出 电 压 和 输 出 电 流；iLa、iLb、iLc为VSG的滤波电感电流。

其中,VSG 控制回路中通过采集LC 滤波器出口处的电压、电流计算输出功率,从而将LC 滤波器引入VSG 序阻抗模型中。

由图1 可以列出VSG 在abc 坐标系下的电路方程:

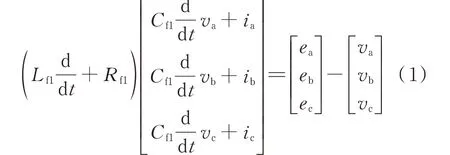
VSG 的控制策略由有功环节和无功环节构成,其控制框图如附录A 图A1（b）所示。有功控制环节模拟同步发电机的机械特性,使VSG 具备惯性和一次调频特性；无功控制环节则模拟同步发电机的电磁特性,使VSG 具备一次调压特性［10］。

根据VSG 的控制框图,其有功环路和无功环路的数学方程如下:

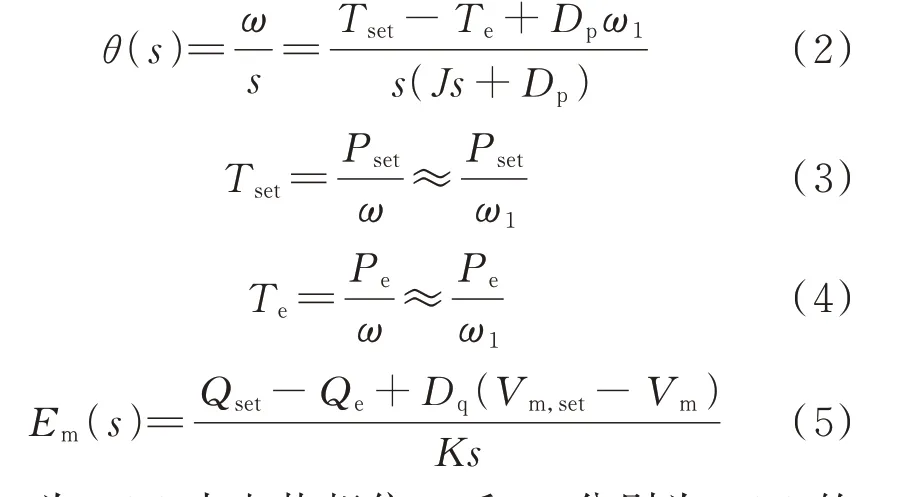
式中:θ为VSG 内电势相位；ω和ω1分别为VSG 的输出角频率和电网额定角频率；Te和Tset分别为VSG 电磁转矩和转矩参考值；Pe和Pset分别为VSG瞬时输出有功功率和有功功率参考值；J为虚拟转动惯量；Dp和Dq分别为有功阻尼系数和无功阻尼系 数；Em为VSG 的 内 电 势 幅 值；Qe和Qset分 别 为VSG 瞬时输出无功功率和无功功率参考值；Vm和Vm,set分别为VSG 输出电压幅值和电压幅值参考值；K为无功惯性系数；s为拉普拉斯变换中的复频率变量。

根据瞬时功率原理可以计算VSG 瞬时输出有功功率Pe和无功功率Qe分别为:

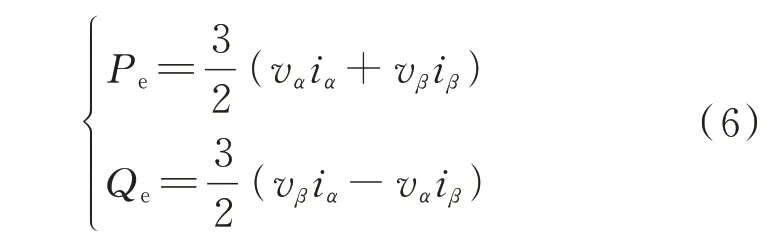
式中:vα、vβ为αβ坐标系下VSG 的输出电压；iα、iβ为αβ坐标系下VSG 的输出电流。

根据VSG 的控制框图可知,VSG 的三相调制波由有功环路和无功环路输出的θ和Em共同决定,其表达式为:

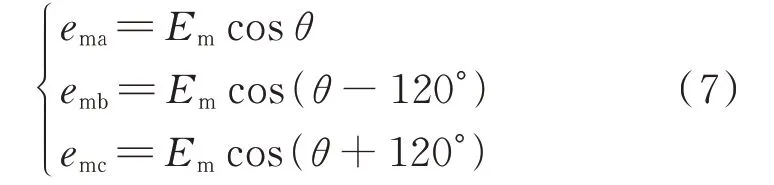
由于VSG 控制存在固有的控制延时问题,故在模型中加入延时环节e-Tdes。由于e-Tdes是一个无理函数,不利于后续分析,故本文采用Pade 近似将其表达为有限维多项式Gd(s)［13］,近似过程见附录B。

不考虑调制过程以及开关过程,则可将VSG 三相调制波视为桥臂电势,即

式中:x=a,b,c。

1.3 基于VSG 控制的构网型逆变器序阻抗建模

文献［9-10］中建立的VSG 序阻抗模型忽略了无功环路以及滤波电路的影响,认为无功环路输出的Em为稳定值,所建立的模型不具备普适性。本文基于谐波线性化构建了考虑滤波电路、无功环路和控制延时的VSG 正、负序阻抗模型,详细推导过程见附录C。

由于考虑频率耦合效应后,最终得到的输出阻抗模型为一个2×2 矩阵,因此需要采用广义Nyquist 定理,增加了稳定性分析的复杂度。另外,本文综合考虑了不同类型逆变器以及联络线阻抗,研究对象并非简单的单机并网系统,系统Nyquist 稳定判据较为复杂,因此本文暂不考虑频率耦合对VSG 序阻抗模型的影响。

若忽略VSG 无功环路和控制延时的影响,认为VSG 内电势幅值为稳态值Em0,即Em(f)=Em0（其中f为频率）,则可得不考虑无功环路及控制延时影响的VSG 正序阻抗ZP1:

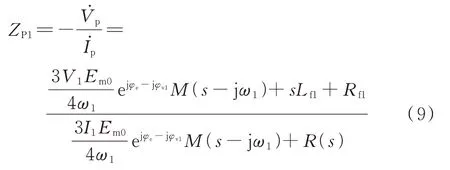
式 中:V1和I1分 别 为 基 波 电 压 和 电 流 幅 值；V̇p和İp分别为正序扰动电压和电流相量；φv1为基波电压的初相角；φe=φ+90°,其中φ为VSG 的桥臂电压与输出电压的相角差；M(s)= 1/[s(Dp+Js)]；R(s)=s2Lf1Cf1+sCf1Rf1+1。

若考虑无功环路的影响,则VSG 内电势幅值将不再是稳定值,此时VSG 正序阻抗ZP2如式（10）所示。若考虑无功环路影响及控制延时,则VSG 正序阻抗ZP3如式（11）所示。

式中:φi1为基波电流的初相角；T(s)=1/(Ks)；K(s)=Dq/(Ks)。

根据正、负序阻抗的转换关系［22］,则可得VSG正序阻抗ZP1、ZP2、ZP3对应的负序阻抗分别为:

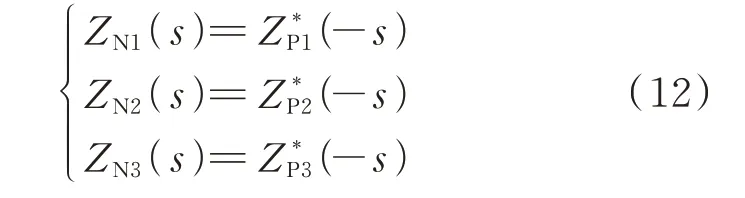
式中:上标“*”表示共轭复数。

以附录A 中基于VSG 控制的构网型逆变器参数建立VSG 序阻抗模型并进行扫频验证。考虑不同控制环节的VSG 正、负序阻抗特性曲线及其扫频测量结果如图2 所示。

由图2 可以得到考虑不同控制环节的VSG 正、负序阻抗特性曲线,三者的比较分析如下:

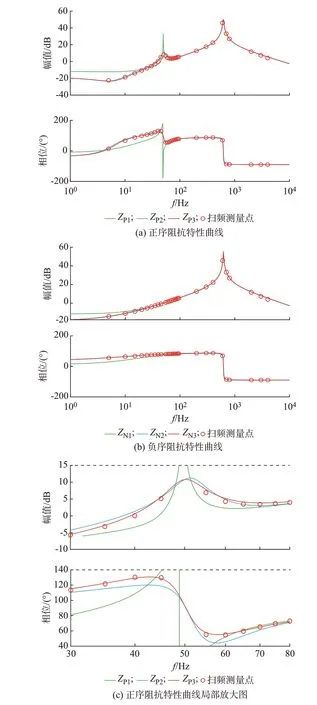
图2 构网型逆变器的正、负序阻抗特性曲线Fig.2 Positive and negative impedance characteristic curves of grid-forming inverter

1）在100 Hz 以上的中高频段,受限于控制带宽,VSG 正、负序阻抗特性因滤波电路的影响而呈现LC 滤波器特性,三者基本一致；

2）在100 Hz 以 下 的 低 频 段,ZP2和ZP3在50 Hz处不存在幅值尖峰和相位突变。考虑无功环路前后,VSG 正序阻抗特性曲线在低频段的幅值和相位均相差较大；

3）在工频50 Hz 附近,考虑控制延时后,ZP3的幅值与ZP2相差较小,ZP3的相位较ZP2更大。

由上述对比分析可知,无功环路和控制延时均会对VSG 的序阻抗特性曲线产生较大影响。若忽略无功环路以及控制延时的影响,可能导致稳定性结果的误判。考虑到扫频测量点与ZP3和ZN3阻抗特性曲线基本重合,在建立VSG 序阻抗模型时不能忽略无功环路及控制延时的影响。

1.4 无功环路参数及控制延时对VSG 阻抗特性曲线的影响

根据图2 的对比分析可知,考虑无功环路和控制延时前后的VSG 阻抗特性曲线的差异主要体现在低频段。为进一步探究考虑无功环路和控制延时的必要性,本小节分析了在不同无功环路参数以及控制链路延时下,VSG 正序阻抗特性曲线在低频段的差异。

令无功阻尼系数Dq从500 减小至120,无功惯性系数K从50 减小至5,VSG 的正序阻抗特性曲线变化如附录D 图D1（a）和（b）所示。通过对比可以发现,随着Dq减小,工频处的幅值尖峰逐渐升高,相位变化逐渐变陡,负阻尼区域不断增加；随着K减小,低频段的幅值逐渐减小,相位逐渐提高,负阻尼区域不断增加。

附录D 图D1（c）所示为控制延时Tde从5×10-5s增大至1×10-3s 的VSG 正序阻抗特性曲线。随着Tde增大,工频附近的幅值变化较小,相位逐渐增大,负阻尼值不断增大。

通过上述分析可知,对于低惯量、弱阻尼的孤岛微网系统,当无功阻尼系数Dq和无功惯性系数K过小,或控制延时Tde过大时,VSG 在低频段的阻尼均会减弱,不利于系统保持稳定。

因此,在对孤岛微网系统进行建模分析时,忽略VSG 无功环路和控制延时的影响可能会导致系统稳定性分析结果与实际截然不同。

1.5 基于电流控制的跟网型逆变器序阻抗建模

典型跟网型逆变器一般采用dq旋转坐标系下的电流前馈解耦控制策略［11］,通过同步旋转坐标锁相 环（synchronous reference frame phase-locked loop,SRF-PLL）跟踪并网点电压的相角与电网保持同步,其控制框图如附录A 图A2 所示,其中:Id和Iq分别为逆变器输出电流的d、q轴分量；Id,ref和Iq,ref分别为逆变器输出电流的d、q轴分量参考值；Kdq为交叉解耦系数；eabc为三相调制波,若不考虑调制过程以及开关过程,则可将eabc视为逆变器桥臂电压。

国内外学者已经对基于电流控制的跟网型逆变器序阻抗建模进行了大量研究,文献［16］详细推导了考虑锁相环的电流控制型并网逆变器序阻抗模型,本文不再赘述推导过程。基于电流控制的跟网型逆变器的正序阻抗Zp如式（13）所示。

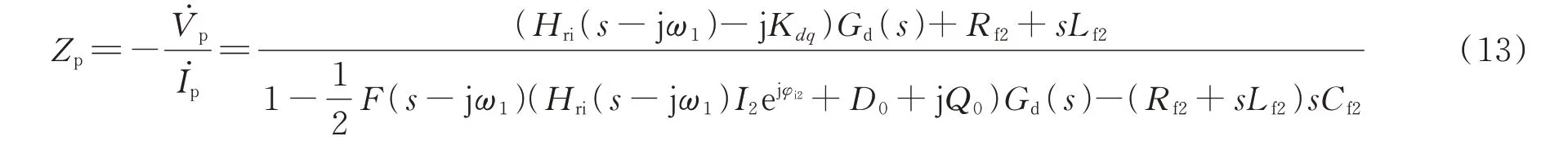
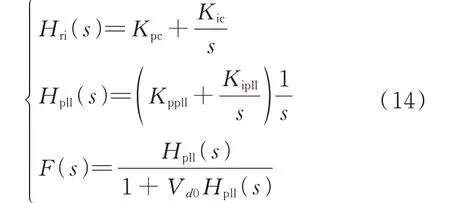
式中:I2和φi2分别为跟网型逆变器输出基波电流的幅值和相角；D0和Q0分别为d、q轴电流比例-积分（PI）控制器的输出稳态值；Kpc和Kic分别为电流PI控制器的比例系数和积分系数；Kppll和Kipll分别为锁相环PI 控制器的比例系数和积分系数；Vd0为跟网型逆变器输出电压d轴分量的稳态值。

跟网型逆变器的负序阻抗为:

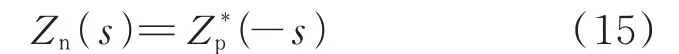
以附录A 中基于电流控制的跟网型逆变器参数建立序阻抗模型并进行扫频验证。跟网型逆变器的正、负序阻抗特性曲线及其扫频测量结果如附录D 图D2 所示。序阻抗模型与扫频测量点基本一致,验证了序阻抗模型的准确性。

2 孤岛微网系统稳定性分析

2.1 Nyquist 稳定判据推导

由于构网型逆变器的外特性表现为电压源,跟网型逆变器的外特性表现为电流源,因此构网型逆变器可以采用电压源Vs1串联等效阻抗Z1的Thevenin 电路替代,跟网型逆变器则采用电流源Is2并联等效导纳Y2的Norton 电路替代［11］,孤岛微网系统的等效阻抗网络模型如图3 所示,其中:VPCC和IPCC分别为并网点电压和电流；IFM和IFL分别为构网型逆变器和跟网型逆变器输出电流；Zg1为构网型逆变器联络线阻抗；Yg2为跟网型逆变器联络线导纳。

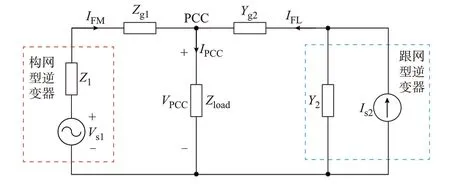
图3 孤岛微网系统等效阻抗网络模型Fig.3 Equivalent impedance network model of islanded microgrid system

根据如图3 所示的等效阻抗网络模型,可以列写出电流IFM、IFL的表达式分别为:

式中:Z2=1/Y2；Zg2=1/Yg2；H1(s)仅与构网型逆变器及其联络线有关；H2(s)仅与跟网型逆变器及其联络线有关；H3(s)与整个孤岛微网系统有关。

由式（18）和式（19）可 知,当H1(s)、H2(s)和H3(s)均稳定时,孤岛微网系统稳定。其中,H2(s)和H3(s)可以看作2 个闭环传递函数,其稳定性取决于开环传递函数Lm1(s) 和Lm2(s)。因此,当H1(s)不存在正实部极点时,若Lm1(s)和Lm2(s)的正、负序Nyquist 图能够满足式（20）,则孤岛微网系统是稳定的。

式中:Z为闭环正实部极点数；N为Nyquist 图顺时针包围点(-1,j0)的周数；P为开环正实部极点数。后文Nyquist 图中标注的字母N、P与上述解释具有相同含义。

2.2 稳态工作点对孤岛微网系统稳定性的影响

根据孤岛微网系统的电路结构和参数可知,跟网型逆变器仅输出有功功率,联络线消耗的无功功率由构网型逆变器补偿,跟网型和构网型逆变器同时为PCC 处负载Zload供能。构网型逆变器联络线电感Lg1、跟网型逆变器联络线电感Lg2以及输出电流d轴分量参考值Id,ref均会对系统稳态工作点造成影响。

由式（19）可知,H1(s)中仅含Z1和Zg1,由于逆变器在设计时会优先保证自身稳定,而线路阻抗Zg1为固定值,因此两者均不含正实部极点。由于加法不会引入额外的正实部极点［19］,且通过计算,在仅改变稳态工作点的情况下H1(s)不含正实部极点,本小节不考虑H1(s)。

在不同稳态工作点下,Lm1(s)和Lm2(s)的负序Nyquist图的变化均不大,且始终没有包围点(-1,j0)。因此,接下来的稳定性分析仅给出Lm1(s)和Lm2(s)的正序Nyquist 图。

2.2.1 构网型逆变器联络线电感Lg1的影响

当联络线电感Lg1增大时,构网型逆变器输出的无功功率也随之增加,输出有功功率不变。在不同的构网型逆变器联络线电感Lg1下,Lm1(s)和Lm2(s)的正序Nyquist 图的变化较小,且始终没有包围点(-1,j0),如附录E 图E1 所示,因此可以判断Lg1对系统稳定性的影响不大。此处仅对不同跟网型逆变器联络线电感Lg2以及输出电流d轴分量参考值Id,ref下的系统稳定性进行详细分析。

2.2.2 跟网型逆变器联络线电感Lg2的影响

增大联络线电感Lg2,跟网型逆变器输出功率不变,构网型逆变器输出无功功率增加。令Id,ref=20 A,跟网型逆变器联络线电感Lg2由5 mH 逐渐增大至10 mH。不同Lg2下Lm1(s)和Lm2(s)的正序Nyquist 图如图4 所示,由图可知,Lg2越大,Lm1(s)和Lm2(s)的正序Nyquist 曲线越接近点(-1,j0)。当Lg2=10 mH 时,Lm1(s)和Lm2(s)的正序Nyquist 曲线包围了点(-1,j0),且正实部极点数P=0。此时,跟网型逆变器因为与联络线之间的交互作用而失稳,进而导致孤岛微网系统无法继续稳定运行,最终系统失稳。

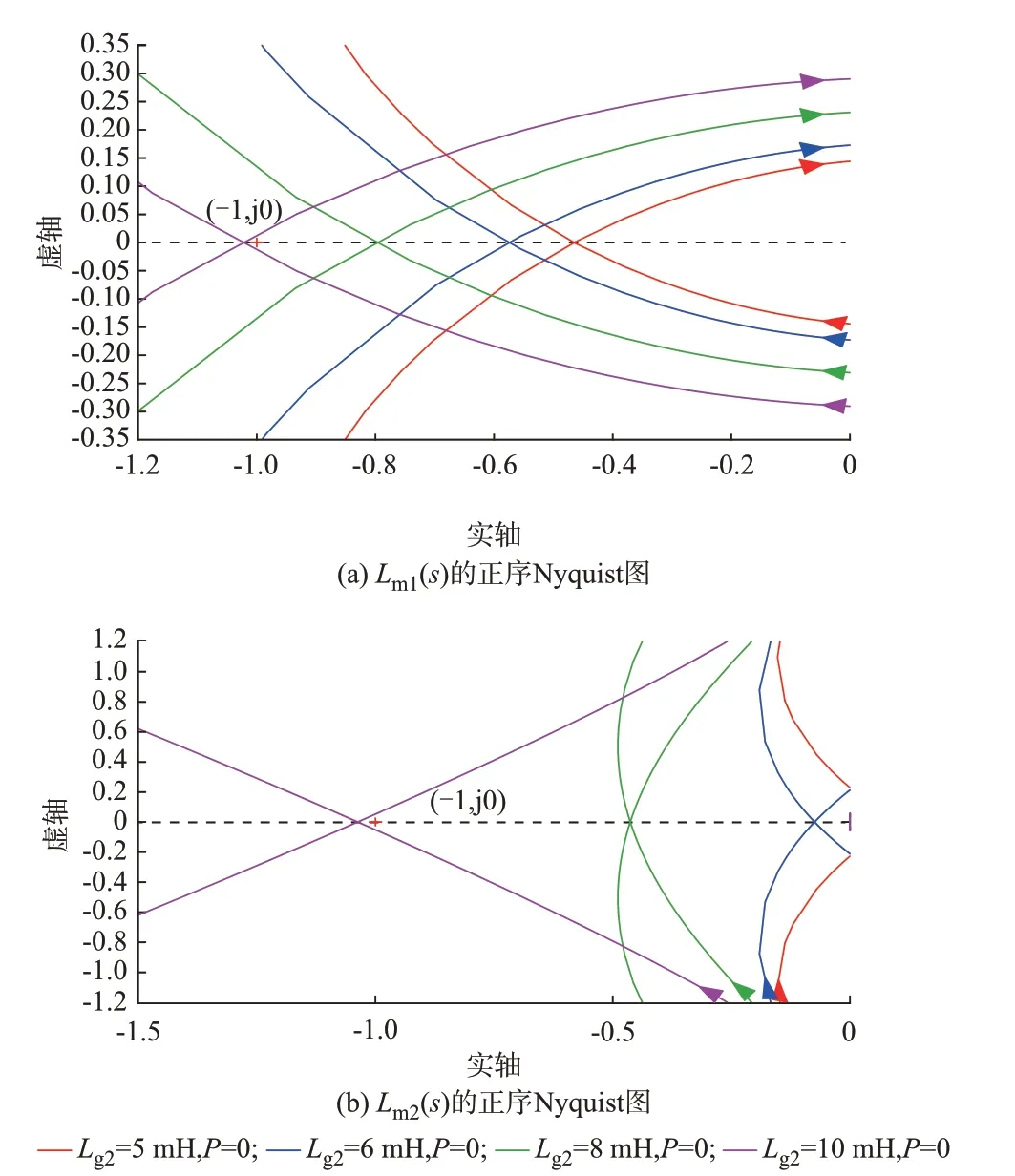
图4 不同Lg2值下Lm1(s)和Lm2(s)的正序Nyquist 图Fig.4 Positive Nyquist plots of Lm1(s)and Lm2(s)with different values of Lg2

通过附录E 图E2 可知,随着Lg2增大,孤岛微网系统等效阻抗［19］的阻抗谐振点逐渐左移,当Lg2增大至10 mH 时,在阻抗谐振点处的等效电阻为-0.093 7 Ω<0 Ω。这 说 明 当Lg2增 大 至10 mH 时,跟网型逆变器由于缺乏阻尼支撑,可能导致锁相环输出频率振荡发散,使得跟网型逆变器无法与构网型逆变器保持同步,最终系统失稳。

2.2.3 跟网型逆变器输出电流d轴分量参考值Id,ref的影响

提高跟网型逆变器输出电流d轴分量参考值Id,ref,跟网型逆变器输出有功功率增加；构网型逆变器输出有功功率减少,输出无功功率增大。令跟网型逆变器输出电流d轴分量参考值Id,ref由20 A 逐渐增大至35 A,Lm1(s)和Lm2(s)均不存在正实部极点。由附录E 图E3 可知,当Id,ref增大时,Lm1(s)和Lm2(s)的正序Nyquist 曲线都存在包围点(-1,j0)的趋势；当Id,ref=35 A 时,Lm2(s)的正序Nyquist 曲线包围点(-1,j0),系统存在失稳风险。

附录E 图E4 所示为不同Id,ref下孤岛微网系统的等效阻抗图。当Id,ref增大至35 A 时,阻抗谐振点的等效电阻为-0.185 6 Ω<0 Ω。因此,跟网型逆变器输出电流d轴分量参考值Id,ref过大,同样会减弱系统阻尼,从而导致锁相环无法保持稳定,最终系统失稳。

2.3 构网型逆变器无功环路参数对系统稳定性的影响

由前文构网型逆变器无功环路参数对其阻抗特性影响的分析可知,Dq和K减小均会在50 Hz 附近引入额外的负阻尼区域,从而导致H1(s)的极点向右半平面移动,最终出现正实部极点,增加了系统失稳风险。

由于Lm1(s)与构网型逆变器的参数无关,仅列出Lm2(s)的正序Nyquist 图。附录F 图F1 所示为不同Dq和K下Lm2(s)的正序Nyquist 图。令K=0.3,逐渐减小Dq,Lm2(s)的正序Nyquist 图始终没有包围(-1,j0)。当Dq减小至190 时,Lm2(s)和H1(s)均含有一个正实部极点,系统失稳。

令Dq=235,逐渐减小K,Lm2(s)同样没有包围(-1,j0)。当K减小至0.2 时,Lm2(s)和H1(s)均含有一个正实部极点,系统失稳。

2.4 跟网型逆变器控制参数对系统稳定性的影响

由前文分析可知,当系统稳态工作点设置不当时,系统缺乏阻尼支撑,若锁相环无法保持稳定,跟网型逆变器将无法与构网型逆变器保持同步,最终导致系统失稳。其中,锁相环作为引起系统失稳的关键因素,合理的控制参数设置对系统保持稳定至关重要。

令Lg2=6 mH,锁相环PI 控制器比例系数Kppll=0.2 不变,积分系数Kipll从300 增大至450,附录F 图F2 所示为Lm1(s)和Lm2(s)的正序Nyquist图。当Kipll增大至450 时,Lm1(s)包围点(-1,j0)两圈,并且不含正实部极点；Lm2(s)逆时针包围点(-1,j0)两圈,并且含有一个正实部极点,此时系统不稳定。

附录F 图F3 所示为不同Kipll下的系统等效阻抗图。随着Kipll逐渐增大,阻抗谐振点逐渐右移,谐振点等效电阻逐渐减小。当Kipll=450 时,谐振点的等效电阻为-0.053 9 Ω<0 Ω。据此可以判断,当跟网型逆变器的锁相环积分系数Kipll增大时,锁相环响应速度提高,但系统阻尼减弱,从而增加了系统失稳的风险。

3 面向孤岛微网稳定性提升的自适应虚拟阻抗设计

由前文对孤岛微网系统的稳定性分析可知,系统缺乏阻尼和惯量支撑是导致系统失稳的根本原因。由于实际系统中主电路参数往往是固定的,本文在跟网型逆变器的控制回路中引入虚拟阻抗［23-24］,从而提高系统阻尼,减小系统失稳风险,其控制框图如图5 所示。图中,Vdq,ref为跟网型逆变器调制波dq轴参考值；iox为跟网型逆变器输出x相电流；e*x为改进后x相桥臂电势；Rv为虚拟阻抗。

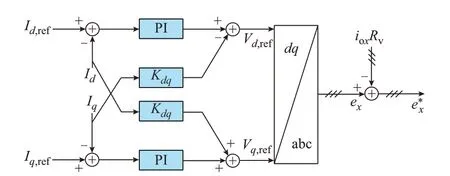
图5 跟网型逆变器改进控制框图Fig.5 Block diagram of improved control of gridfollowing inverter

引入虚拟阻抗后,跟网型逆变器的桥臂电势为:

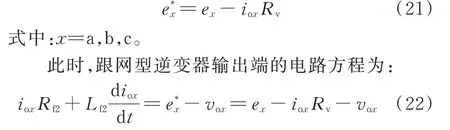
由式（22）可知,控制回路中引入的虚拟阻抗Rv可等效为跟网型逆变器输出端的串联电阻,从而等效地提高了系统阻尼。引入虚拟阻抗后,跟网型逆变器的阻抗特性曲线如附录G 图G1 所示。随着虚拟阻抗系数kv逐渐提高,虚拟阻抗Rv随之逐渐增大,跟网型逆变器在低频段的正序阻抗幅值明显提高,正序阻抗相位绝对值明显减小,阻抗特性容性部分减少,有利于系统保持稳定。

基于前文分析可知,跟网型逆变器联络线电感Lg2及其输出电流d轴分量参考值Id,ref对系统稳定性的影响较大。因此,为了减小虚拟阻抗对系统稳态工作点的影响,可以根据Lg2和Id,ref的稳定边界值选取虚拟阻抗Rv,从而对系统阻尼进行自适应补偿,其表达式为:

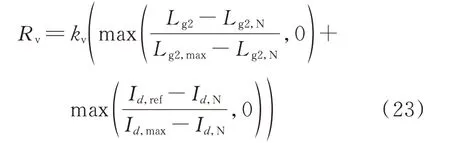
式中:Lg2,N和Id,N分别为跟网型逆变器联络线电感和输出电流d轴分量的额定值；Lg2,max和Id,max分别为经过阻抗稳定性分析后,得出的跟网型逆变器联络线电感和输出电流d轴分量的稳定边界值。

假设Lg2=Lg2,max时,系统等效负电阻为Req1；Id,ref=Id,max时,系统等效负电阻为Req2。为了给系统提供足够的阻尼补偿,虚拟阻抗Rv的取值应大于Req1和Req2。另外,由于Rv变化时会引入短暂的过渡过程,Rv的取值不宜过大。因此,虚拟阻抗Rv应满足下式:

式中:abs（·）表示取绝对值。

附录G 图G2 所示为不同Lg2和Id,ref下的虚拟阻抗Rv取值。当Lg2和Id,ref发生变化时,Rv能够自动修改取值,在减小对系统影响的同时,为系统提供足够的阻尼补偿。

4 仿真及实验验证

为了验证上述理论分析的正确性,本文在MATLAB/Simulink 中 按 照 附 录A 表A1—表A3 所示的系统参数搭建了仿真模型。最后,基于RTLAB 实验平台进行半实物仿真,验证了理论分析和仿真结果的准确性。

4.1 基于MATLAB/Simulink 的仿真验证

4.1.1 与系统稳态工作点有关的仿真验证

附录H 图H1 所示为在不同Lg1下,构网型逆变器和跟网型逆变器本地dq坐标轴的相角差δ2（以跟网型逆变器为基准）以及构网型输出有功功率、无功功率波形。构网型逆变器的Lg1增大后,其输出无功功率随之增加,在经过短暂的过渡过程后,构网型逆变器始终能够保持稳定运行,与理论分析结果一致。

图6（a）所示为在不同Lg2下,相角差δ2以及跟网型逆变器锁相环输出频率f2和输出电流d轴分量Id2的仿真波形。当Lg2由6 mH 增大至8 mH 后,δ2、f2和Id2经过短暂的减幅振荡后趋于稳定；而当Lg2增大 至10 mH 后,δ2、f2和Id2均 出 现 了 严 重 的 振 荡 现象,系统失稳,仿真结果与Nyquist 稳定性分析结果一致。

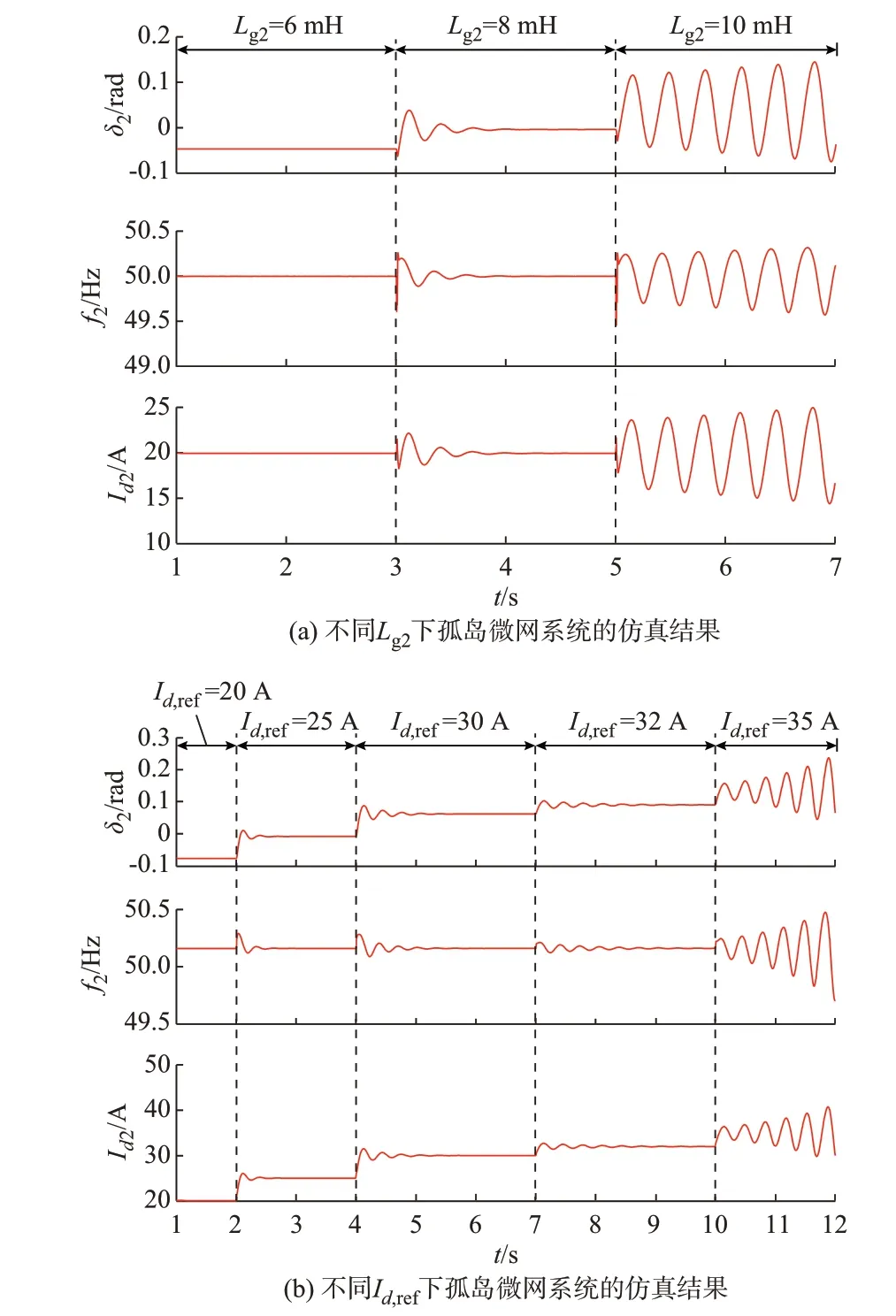
图6 不同稳态工作点下孤岛微网系统的仿真结果Fig.6 Simulation results of islanded microgrid system at different steady-state points

图6（b）所示为在不同Id,ref下的仿真波形。当Id,ref增大至32 A 时,δ2、f2和Id2经过短暂振荡过程后能 够 迅 速 保 持 稳 定；当Id,ref增 大 至35 A 时,δ2、f2和Id2逐渐发散,系统失稳,仿真结果与Nyquist 稳定性分析结果一致。

4.1.2 与构网型逆变器控制参数有关的仿真验证

附录H 图H2 所示为不同无功环路参数下,令Id,ref=30 A,Lg1由5 mH 提高至7 mH 时的仿真波形。由前文分析可知,Lg1增大时,仅增大构网型逆变器无功功率输出。当Dq=190、K=0.3 或Dq=235、K=0.2 时,Lg1提高至7 mH 后,构网型逆变器输出功率逐渐振荡发散,最终无法与跟网型逆变器保持同步,系统失稳,与理论分析结果一致。

4.1.3 与跟网型逆变器控制参数有关的仿真验证

附录H 图H3 所示为不同Kipll下改变Id,ref的仿真波形。随着锁相环积分系数Kipll的增加,Id,ref变化时锁相环响应速度变快,但振荡幅值增大,稳定时间延长。当Kipll=450 时,Id,ref由28 A 增加至30 A,锁相环输出频率振荡发散,系统失稳,仿真结果与Nyquist 稳定性分析结果一致。

4.1.4 与虚拟阻抗控制策略有关的仿真验证

附录H 图H4 所示为不同kv下改变Lg2和Id,ref孤岛微网系统的仿真结果。由图H4（a）可知:kv越大,虚拟阻抗增加的系统阻尼越大；Lg2变化时仿真波形的振荡幅值越小,过渡时间越短。

由附 录H 图H4（b）可知,当kv=0.1,Id,ref增大至35 A 时,Rv=0.1 Ω,锁相环输出频率振荡发散,系统失稳。由附录E 图E4 可知,Id,ref=35 A 时系统等 效 电 阻 绝 对 值 为abs(-0.185 6 Ω)>0.1 Ω,当 取kv=0.1 时（蓝线）,虚拟阻抗无法提供足够的阻尼支撑使系统保持稳定。因此,将kv的取值增大为0.3（红线）,虚拟阻抗提高至Rv=0.3 Ω>0.185 6 Ω,跟网型逆变器输出电流经过短暂振荡后逐渐收敛,系统能够保持稳定,验证了虚拟阻抗取值范围式（24）的有效性。

4.2 基于RT-LAB 的实验验证

如图7（a）所示,跟网型逆变器联络线电感Lg2由8 mH 大至10 mH 后,其输出电流产生增幅振荡,系统失稳。如图7（b）所示,跟网型逆变器输出电流参考值Id,ref由32 A 升高至35 A 后,其输出电流同样产生增幅振荡,系统无法保持稳定。不同Id,ref下跟网型逆变器输出电流波形（Kipll=450）如附录H 图H5 所示,当跟网型逆变器锁相环积分系数Kipll=450 时,Id,ref由28 A 提 高 至30 A 后,其 输 出 电 流 逐 渐振荡发散,系统失稳。

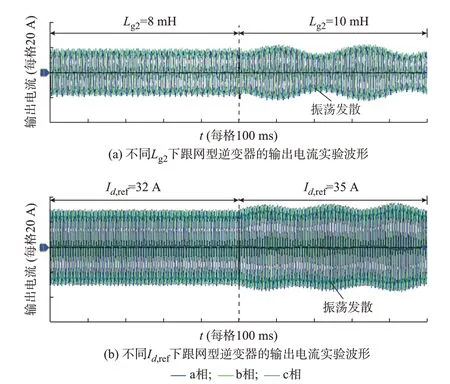
图7 不同稳态工作点下跟网型逆变器的输出电流实验波形Fig.7 Experimental waveforms of output current for grid-following inverter at different steady-state points

如附录H 图H6 所示,在跟网型逆变器控制回路中加入虚拟电阻后（kv=0.3）,Id,ref由32 A 升高至35 A,其输出电流经过短暂的振荡衰减后能够保持稳定。

由上述分析可知,RT-LAB 实验结果与理论分析和仿真结果一致,验证了前文所得结论的准确性以及虚拟电阻设计方法的有效性。

5 结语

本文针对无电网支撑且逆变器主导的孤岛微网系统,基于谐波线性化建立了序阻抗模型；基于Nyquist 稳定判据探究了系统稳态工作点和控制参数对系统稳定性的影响规律；并引入了虚拟阻抗控制策略,等效提高了系统阻尼,增强了系统稳定性。主要的工作与结论如下:

1）建立了由逆变器主导的孤岛微网系统序阻抗模型,分析了无功环路以及控制延时对VSG 阻抗特性的影响:无功环路参数Dq和K减小会增加工频附近的负阻尼区域；控制延时Tde过大会使得工频附近的负阻尼值增加；无功环路参数或控制延时均对VSG 阻抗特性有显著影响。

2）基于系统等效阻抗网络模型构建了Nyquist稳定判据；充分考虑了系统参数对系统稳态工作点的影响,分析了系统稳态工作点对系统稳定性的影响规律；当跟网型逆变器联络线电感Lg2及其输出电流d轴分量参考值Id,ref过大时,系统缺乏阻尼支撑,从而无法保持稳定运行。

3）基于Nyquist 稳定判据分析了逆变器控制参数对系统稳定性的影响。当VSG 无功环路参数Dq和K过小时,构网型逆变器无法为系统提供稳定的频率支撑,进而导致系统失稳；跟网型逆变器锁相环积分系数Kipll过大时,锁相环响应过快,削弱了系统阻尼,不利于系统保持稳定。

4）在跟网型逆变器控制回路中加入虚拟阻抗Rv,基于参数稳定边界及其对应的等效负电阻给出了Rv的设计方法,并通过仿真和实验验证了Rv在系统稳态工作点变化时对系统的自适应阻尼作用。

本文采用了传统Nyquist 稳定判据进行稳定性分析,每一次分析前都需要计算一次正实部极点数,降低了稳定性分析效率,通过采用改进稳定判据［25-26］,能够在一定程度上减缓上述问题。另外,本文仅考虑了由单个构网型逆变器和跟网型逆变器构成的孤岛微网系统,对于同时含有多个两种类型逆变器的微网系统的稳定性分析还有待研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。