弱电网下计及锁相环影响的并网逆变器稳定性提升方法
2022-02-02姜云龙司鑫尧史鸿飞竺明哲
姜云龙,司鑫尧,史鸿飞,竺明哲,葛 乐
(1. 国网江苏省电力有限公司电力科学研究院,江苏省南京市 211103;2. 南京工程学院电力工程学院,江苏省南京市 211167)
0 引言
近年来,可再生能源发电技术广受关注[1-2],并网逆变器作为可再生能源发电单元与公共电网之间的接口,其主要目标是向电网注入稳定且高质量的电流[3]。在某些场合下,逆变器与电网之间的传输线路很长,这时电网阻抗不可忽略,系统呈现弱电网特性。电网强度由短路比(SCR)表示,SCR 小于等于10 的电网可视为弱电网[4]。由于电网阻抗的存在,公共耦合点(point of common coupling,PCC)电压畸变,严重影响并网逆变器的控制性能,甚至导致不稳定现象[5-6]。
在弱电网下,PCC 电压存在扰动,当并网逆变器工作在单位功率因数下时,该扰动大小随电网阻抗、并网电流的增大而增大,从而影响锁相环(phase-locked loop,PLL)输出相位的动态性能[7],具体表现为并网逆变器的系统dq轴坐标系与控制器dq轴坐标系不重合[8],进一步导致并网电流发生畸变,并网功率振荡,危害并网系统稳定运行。文献[9]建立了弱电网下考虑PLL 影响的并网逆变器等效阻抗模型,并指出PLL 引入的负阻抗会降低并网逆变器输出阻抗的幅值和相角,从而降低系统的稳定裕度。为提高并网系统稳定性,可以对PLL 或并网电流控制环进行改进。
一方面,采用降低PLL 带宽的方法可有效减小负阻抗带来的不利影响[10-11],但是降低PLL 带宽会恶化系统的动态性能。因此,文献[12-13]通过改变PLL 结构,进一步提高了PLL 的抗干扰能力,使其在较高带宽下仍有良好的稳定性。但这些方法会使PLL 结构复杂化,不利于并网逆变器参数设计。为此,文献[14]通过改变PLL 的输入,实现PLL 与电网阻抗的解耦,但此方法需要对电网阻抗进行实时测量,增加了硬件成本与算法的复杂性。
另一方面,为了在不改变PLL 结构与参数的前提下增强并网系统的稳定性,文献[15-16]通过串并联虚拟阻抗的方法对并网逆变器电流环输出阻抗进行重塑,防止并网逆变器输出阻抗与电网阻抗在交截频率处因相位裕度不足而不稳定。文献[17-19]通过建立弱电网下考虑PLL 影响的并网逆变器小信号模型揭示了PLL 对并网逆变器电流控制环的影响程度和影响机理。文献[17]提出在并网电流和调制电压处加入小信号补偿的方法,减小并网电流和调制电压处的扰动,从而增强系统对低频谐波的抑制能力,但随着频率的升高,此方法对交截频率处相位裕度的提升效果减弱。电网阻抗宽范围变化时,如果交截频率处的相位裕度不足,该频率处的谐波会被放大[20]。
为保证逆变器在电网阻抗宽范围变化的条件下都能向电网注入稳定且高质量的电流,本文在小信号补偿控制的基础上,在调制电压处额外加入微分补偿通路,由于微分项在实际应用中较难实现且对噪声敏感,本文采用非理想广义积分器(generalized integrator,GI)等效替代。通过对比传统无补偿、小信号补偿和本文所提改进小信号补偿3 种控制策略下的并网逆变器等效输出阻抗特性可知,所提改进小信号补偿控制进一步提升了并网系统的稳定性,且在全频段都能保持良好的稳定裕度。
1 弱电网下考虑PLL 影响的并网逆变器模型
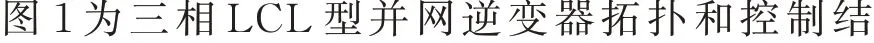

图1 LCL 型并网逆变器拓扑和控制结构Fig.1 Topology and control structure of LCL-type grid-connected inverter
为了有效抑制LCL 滤波器引入的谐振,本文采用电容电流反馈的有源阻尼策略[21]。电流环采用比例-积分(PI)控制器,其传递函数Gi(s)为:

式中:kp为比例增益系数;ki为积分增益系数。
在弱电网条件下,电网电压相角θ与锁相环输出相角θpll之间存在相角偏差Δθ。Δθ的存在将dq坐标轴分为系统dq坐标轴和控制器dq坐标轴[8-9],分别用上标s 和上标c 来表示。由文献[20]的分析可知PLL 小信号模型为:
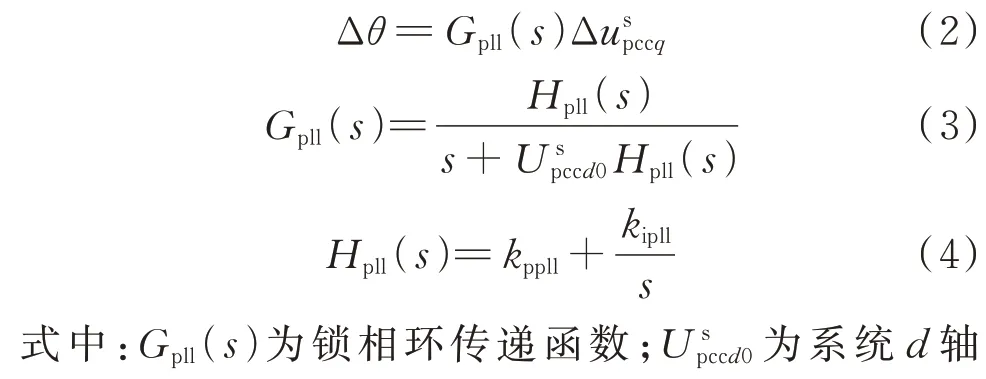




式中:Gx1(s)和Gx2(s)为电流环等效传递函数;Gde(s)为控制延时函数。
根据附录A 图A1 可得系统环路增益函数TA(s)为:

2 基于阻抗的稳定性分析
2.1 阻抗稳定性判据
文献[23]指出,弱电网环境下,并网系统可等效为并网逆变器输出阻抗和电网级联的形式,由于PLL 的负阻抗特性仅出现在q轴,因此只需对q轴输出阻抗进行分析,等效电路如附录A 图A2 所示。电网阻抗中电阻部分对并网系统的稳定性有利,因此,本文在最恶劣情况下进行阻抗分析,即分析电网阻抗Zgqq(s)为纯电感(Lg)时并网逆变器的稳定性。
由附录A 图A2 可知,并网电流可表示为:

2.2 小信号补偿控制稳定性分析


Lg为6、16、24 mH(对应的SCR 分别为7.7、2.9和1.9)时,Zqq1(s)与Zgqq(s)在100 Hz 附近(下文称低频段)的交点分别为(188 Hz,-43.5°)、(113 Hz,-63.2°)和(92 Hz,-68.4°),对应的相位裕度分别为46.5°、26.8°和21.6°。采用小信号补偿控制后,相位裕度分别提升了17.9°、26.7°和32.6°,可见加入小信号补偿后并网逆变器等效输出阻抗在低频段的幅值和相位都有了显著的提升,增强了系统在低频段的稳定性。Lg为6、16、24 mH(对应的SCR 分 别 为7.7、2.9 和1.9)时,Zqq1(s)与Zgqq(s)在900 Hz 附近(下文称高频段)的交点分别为(944 Hz,-86.5°)、(888 Hz,-79.2°)和(875 Hz,-65.2°),对 应 的 相 位 裕 度 分 别 为3.5°、11.8°和24.8°。采用小信号补偿控制后,相位裕度分别提升了3.2°、8.0°和17.9°,可见高频段相位裕度的提升明显低于低频段。此外,随着频率的升高,小信号补偿对并网逆变器相位裕度的提升逐渐降低,在Lg=6 mH 时,交截频率处的相位裕度仅为3.5°。因此,加入小信号补偿后的并网逆变器在阻抗宽范围变化的情况下无法一直保证足够的相位裕度,在高频段存在谐波放大的风险。
3 并网逆变器改进小信号补偿控制
通过第2 章的分析可知,小信号补偿对高频段相位裕度的提升有限,一旦逆变器等效输出阻抗与电网阻抗交截频率处相位裕度不足,该频率附近谐波易被放大。为了提高并网系统的稳定性,本文提出在小信号补偿的基础上分别在并网电流处和调制电压处额外加入微分补偿通路作为两种改进小信号补偿方案。由于并网电流和调制电压处的控制框图类似,此处只给出调制电压处的控制框图如附录A图A6 所示。其中,k1为调制电压的微分项补偿增益。
由于微分项在实际运用中较难实现且对噪声敏感,文献[25]提出用积分传递函数等效替代微分项。
农村教师由于工作量大,需要完成的任务指标多,对于学生的作业方面重视程度不够。同时,教师对于学生的情况没有很好地把握,布置作业有时急于应付形式,很少考虑到时效性。此外,数学教师参考资料缺乏,不关注学生之间的差异,所有练习采用“一刀切”模式。
3.1 微分项等效替换原理分析
非理想GI 的传递函数如式(13)所示。

式中:ωc为截止角频率;ω∗为最大增益点处的角频率。
根据式(13)绘制出非理想GI 的波特图,如附录A 图A7 所示。由图A7 可 知,当角频率ω≪ω∗时,非理想GI 可以很好地替代微分项,通过设置ωc来调节ω∗处的增益,可有效降低噪声的影响。为了使非理想GI 在Nyquist 频率内都能保持微分特性,ω∗应等于πfs,其中,fs为采样频率。
3.2 基于非理想GI 的改进小信号补偿控制
3.2.1 方案及参数选择
图2 为分别在并网电流和调制电压处加入微分补偿通路后的q轴闭环电流控制小信号模型。其中,k2为调制电压的微分项补偿增益;Gcom,gi(s)为微分补偿项,可表示为:
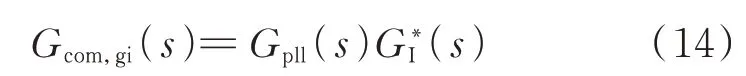
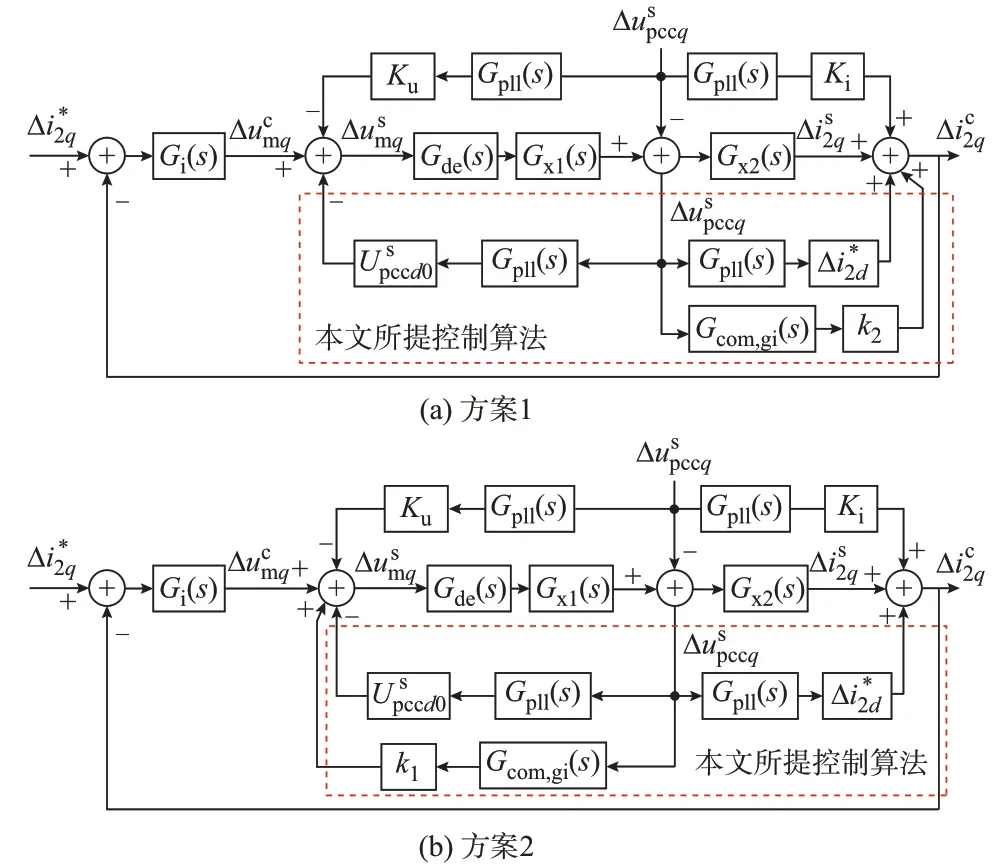
图2 加入微分补偿后的q 轴闭环电流控制小信号模型Fig.2 Small-signal model of q-axis closed-loop current control with derivative compensation
为研究分别从并网电流处和调制电压处加入微分补偿通路对并网逆变器等效输出阻抗的影响,本文定义图2(a)、(b)中两种控制方式分别为方案1 和方案2,其对应的输出阻抗波特图分别如图3(a)、(b)所示。由图3(a)可知,在并网电流处加入微分补偿通路对并网逆变器等效输出阻抗高频段的相位有所提高,且随着k2的增大并网系统高频段稳定性越好。但该方法会降低低频段的相位,且随着k2的增大低频段相位下降越明显。该方法无法保证并网逆变器的相位始终高于-90°,不利于并网系统在低频段的稳定性。
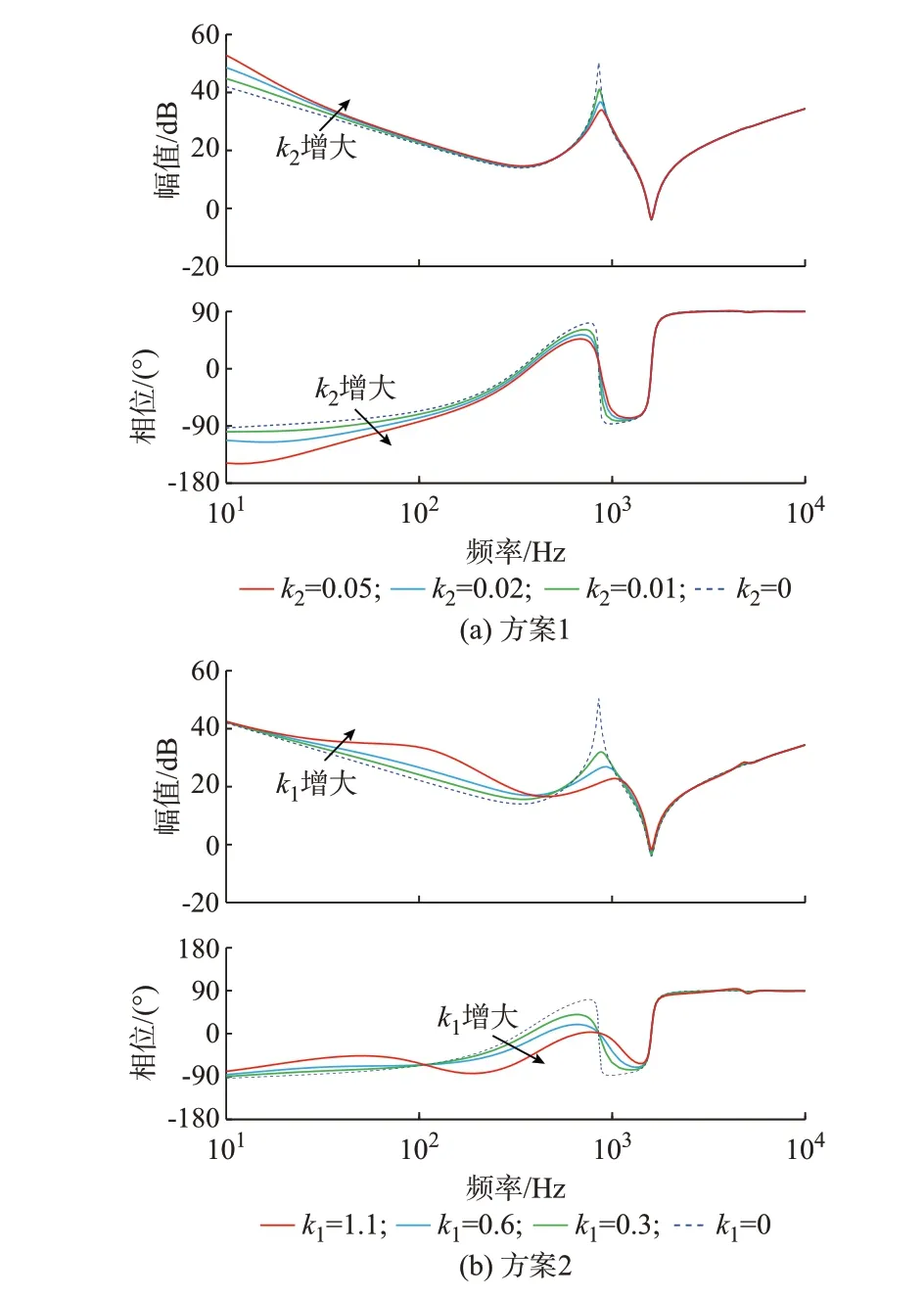
图3 加入微分补偿后的输出阻抗波特图Fig.3 Bode diagram of output impedance with derivative compensation
3.2.2 不同控制方式下的并网逆变器输出阻抗分析
图4 为分别采用所提改进补偿控制、小信号补偿控制和无补偿控制下考虑PLL 影响的并网逆变器输出阻抗和电网阻抗波特图,其中,Zqq2(s)为加入3.2.1 节所提改进小信号补偿后的并网逆变器等效输出阻抗。
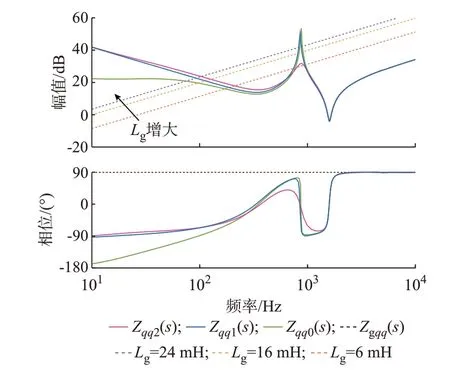
图4 采用不同控制方式下的输出阻抗波特图Fig.4 Bode diagram of output impedance with different control modes
由图4 可见,Lg为6、16、24 mH(对应的SCR 分别为7.7、2.9 和1.9)时,Zqq2(s)与Zgqq(s)在低频段的交点分别为(211 Hz,-42.3°)、(127 Hz,-60.9°)和(103 Hz,-65.8°),对应的相位裕度分别为47.7°、29.1°和24.2°,与小信号补偿相比,虽然阻抗相位略有下降,但由于阻抗幅值的提升,低频段交截频率处相位裕度略有提升。在高频段,仅在Lg=6 mH 时Zqq2(s)与Zgqq(s)存在交点(926 Hz,-38.3°),对应的相位裕度为51.7°,相比于小信号补偿,相位裕度提升了48.2°,可见所提改进小信号补偿对高频段相位裕度提升明显。综上所述,采用本文所提改进小信号补偿控制方法增强了并网系统的稳定性,使并网逆变器在阻抗宽范围变化的弱电网环境下始终能保持稳定运行。
4 实验验证
为验证本文理论分析的正确性以及所提改进小信号补偿控制策略的有效性,利用RT-LAB 硬件在环实验平台搭建了电压有效值为220 V、频率为50 Hz、额定容量SB为10 kW 的三相LCL 型并网逆变器模型和阻抗可调的弱电网环境,控制器采用TMS320F28335 DSP 芯片进行实验验证,具体平台结构如附录A 图A8 所示,主要实验参数如附录A表A1 所示,实验参数与分析所用的参数完全一致。
附录A 图A9 给出Lg=0 mH 时的三相并网电流i2,abc和a 相PCC 电压upcc,a实验波形,可见在Lg=0 mH 时原系统控制性能良好。


图5 Lg=6 mH 时改进小信号补偿下的实验波形Fig.5 Experimental waveforms with improved smallsignal compensation when Lg=6 mH


由图4 可知,采用本文所提改进小信号补偿控制后,并网逆变器等效输出阻抗幅值曲线在850 Hz附近有所降低。为验证阻抗幅值降低对并网逆变器该频段谐波抑制能力的影响,附录A 图A13 给出Lg=16 mH 时含有3%的17 次(850 Hz)电网背景谐波下i2,abc和upcc,a的实验波形。可见,在电网电压含有3%的17 次谐波下,采用本文所提改进小信号补偿方法,并网逆变器依然能够保持稳定运行。微分补偿通路的引入导致阻抗幅值下降,其阻抗幅值与小信号补偿相比存在一定的差距,但该差距对并网逆变器在该频段的谐波抑制能力的影响不大。

5 结语
本文针对弱电网下考虑PLL 影响的并网逆变器稳定性控制问题展开了研究,提出在逆变器q轴调制电压或并网电流处额外加入一条微分补偿通路,以提升并网逆变器的稳定性。由于微分项在实际应用中较难实现且对噪声敏感,采用非理想GI 等效替代。经分析可得如下结论:
1)与仅采用小信号补偿相比,所提方法在全频段都能保持良好的稳定裕度,有效解决了小信号补偿在高频段交截频率处因相位裕度不足而导致的谐波放大的问题。
2)在q轴并网电流处加入微分补偿通路的方法会降低逆变器在低频段的相位,不利于并网系统的稳定运行。而在q轴调制电压处加入微分补偿通路的方法可有效提高逆变器等效输出阻抗高频段相位,且逆变器等效输出阻抗的相位始终高于-90°。
所提方法无须改变PLL 参数与结构,且并网系统在电网阻抗宽范围变化下始终能够保持良好的稳态和动态性能。虽然微分补偿系数的增大可提高并网系统高频段稳定性,但过大的补偿量会导致并网逆变器在低频段内因相位裕度不足而出现谐波放大的现象。因此,补偿系数的大小须折中确定。
所提方法在非单位功率因数并网、动态过程中的有效性还需要进一步评估。同时,由于同步旋转坐标锁相环有限的抗干扰能力,电网电压不平衡、谐波等对其性能会有一定影响。在后续研究工作中,将对电网电压不平衡或存在谐波条件下PLL 的滤波、鲁棒性以及在此基础上的并网逆变器稳定性提升方法进行深入研究。
本文研究受到国网江苏省电力有限公司科技项目(J2021008)资助,特此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
